SdC(b) (LM PA)

La quinta esercitazione prevede lo studio di un arco con il software SAP. L’arco rappresenta una tipologia di struttura che lavora a sforzo normale, grazie alla sua geometria, che gli permette di lavorare non per massa, ma per forma riuscendo a superare grandi luci dato che non funziona a flessione ottimizzando anche l’impiego di materiale.

Per il disegno di un arco a tutto sesto si è utilizzato il programma AUTOCAD, grazie al quale è stato possibile realizzare un arco con una luce di 6m.  Una volta realizzato il modello, si è salvato il file in formato DXF e poi lo si è importato direttamente sul programma SAP. 

Dato che il modello di riferimento, in tal caso, è un arco a tre cerniere, si è proceduto con l’assegnare in corrispondenza della linea d’imposta due cerniere esterne: dopo aver selezionato i due punti -> Assign -> Joint -> Cerniera

Per inserire la cerniera in chiave il procedimento prevede di selezionare il segmento precedente e quello successivo al punto che coincide con la chiave dell’arco e poi impostare il comando: Assign -> Release -> spuntare una volta la casella “end” e una volta la casella “start” in corrispondenza del Momento 33 per il rilascio del momento, che deve essere assente.

Successivamente si è assegnata una sezione alla struttura; si è optato per una sezione rettangolare in calcestruzzo pari a 0,3x0,4 m.

L’arco è stato, poi, sottoposto ad un carico uniformemente distribuito ed impostato attraverso i seguenti comandi: si è selezionato l’arco -> Assign -> Frame Loads -> Distributed -> impostare un carico Q trascurando il peso proprio della sezione dell’arco -> in corrispondenza della voce Direction si è impostata la condizione: Gravity Projected per indicare un carico pari a 10 KN/m non distribuito sulla lunghezza dell’arco, ma sulla sua proiezione a terra.

Si è avviata l’analisi e si è visto che il carico totale pari a 10 KN/m x 6m = 60 KN è stato ripartito equamente in corrispondenza dell’imposta; se si considera metà arco qxl = 10 KN/m x 3m (metà luce) = 30 KN pari alla metà del carico totale, mentre in chiave si ha qxl/2 = 10 KN/m x 3m /2 = 15 KN.

ARCO PARABOLICO

Dopo aver rappresentato sul programma SAP un arco a tutto sesto si è proceduto con la realizzazione di un modello di un arco parabolico (di equazione y= ax²+bx+c) con tre cerniere e caricato anche esso con un carico q uniforme. Dai risultati che fornirà il software SAP ci si aspetta che l’arco assuma un comportamento funicolare, per cui momento flettente e taglio sono nulli, mentre tutto il carico viene trasformato in sforzo normale.

Si è disegnato un arco usando il programma AUTOCAD con il comando “Spline” con luce pari a 6 metri, uguale a quella dell’arco a tutto sesto rappresentato precedentemente. Successivamente lo si è salvato in formato DXF ed importato su SAP.

Anche in questo caso sono stati applicati i vincoli cerniera all’imposta dell’arco.

In chiave è stata inserita una cerniera interna seguendo la stessa modalità descritta per l’arco a tutto sesto.

Si è selezionato l’intero arco ed è stata adottata una sezione in calcestruzzo di dimensioni pari a 30 cm x 40 cm.

È stato applicato un carico distribuito pari a 10 KN/m, senza considerare il peso proprio dell’arco, e non distribuito su tutta la lunghezza dell’arco stesso, ma solo sulla sua proiezione a terra.

Si è avviata l’analisi grazie alla quale è stato possibile notare che la reazione vincolare orizzontale, considerando metà arco (per una luce = 3m) risulta essere uguale a quella dell’arco a tutto sesto, ovvero 30KN, che deriva da: 10KN/m x 3m. Per ciò che riguarda la reazione verticale essa non è pari a ql/2, ma deriva da: ql²/2f dove f sta ad indicare la freccia dell’arco che nell’arco parabolico è diversa dalla luce l.

Per questa esercitazione ci viene richiesto di andare a risolvere una struttura ad arco con il software SAP.
Questo tipo di struttura, reagisce grazie alla propria geometria e tende a lavorare solo con sforzo normale, quindi in maniera omogenea su tutta la sezione, avendo così un’ottimizzazione del materiale (nel momento per esempio, le fibre al centro della sezione lavorano meno rispetto quelle esterne).
Data l’impossibilità di utilizzare il programma per disegnare linee curve, utilizzeremo un programma CAD (autoCAD, Rhino, etc.).
Una volta esportato il file (.dxf, .iges) importiamolo sul programma SAP.
Svolgiamo prima il caso dell’arco a tutto sesto, ovvero quando la freccia è pari a metà della luca (semicircolare), dimostrando che tra le reazioni vincolari (appoggiato-appoggiato) risulteranno anche azioni orizzontali, quindi spingenti lateralmente.
Una volta preso metà arco in considerazione (tenendo conto che il concio di chiave è rappresentabile come una cerniera interna), possiamo dimostrare come la reazione verticale sull’appoggio risulterà uguale a metà carico equamente distribuito sulla proiezione dell’arco (quindi q*l, dove l è metà luce), mentre tramite equilibrio dei momenti dimostriamo come la reazione orizzontale sull’appoggio (verso l’interno) risulterà uguale a ql/2.

Importiamo il disegno su SAP.

Mettiamo i vincoli di appoggio agli estremi.

Andiamo ad inserire una cerniera interna sul concio di chiave.

Applichiamo ora una sezione in cemento armato all’intero arco (ottimizzato già con la stessa sezione su tutta la lunghezza).

Andiamo a togliere il peso proprio della struttura e a applicare un carico distribuito q pari a 10 Kn/m sulla proiezione dell’arco a terra, non sulla lunghezza dell’arco (gravity projected).

Calcoliamo ora le reazioni.

I risultati corrispondono a quelli descritti nell’analisi spiegata sopra.

Analizziamo ora il caso di un arco parabolico, ovvero un arco il cui andamento corrisponde all’andamento di una parabola, quindi di equazione y(x)=ax^2+bx+c.

Dopo averlo disegnato tramite SpLine su autoCAD, importiamo il file su SAP.

Applichiamo i vincoli (appoggio - appoggio).

Applichiamo una cerniera interna nel concio di chiave.

Applichiamo la sezione come nel caso precedente,

e anche il carico distribuito sulla proiezione dell’arco.

Calcoliamo le reazioni vincolari.

Notiamo come mentre la reazione verticale rimane la stessa, l’orizzontale ovviamente sarà diversa, dato che in questo caso, non corrisponde allo sforzo normale.  Tale reazione sarà uguale a ql^2/2f (dove f corrisponde alla freccia dell’arco 6m nel nostro caso).

Proviamo ora ad eliminare le azioni spingenti lateralmente tramite l’addizione di due mensole esterne.
Provando a calcolare manualmente le razione di questa situazione, siamo riusciti a trovare che per eliminare totalmente queste spinte le mensole devono avere una lunghezza, in proiezione sull’asse X pari al prodotto della semiluce e la radice quadrata del rapporto tra carico q sull’arco e carico q sulla mensola:

b=l*sqrt(q1/q2)

Immaginando q1=q2, per eliminare lo sforzo orizzontale avrei dovuto inserire mensole di una lunghezza tale da avere una proiezione sull’asse X di 3m.

Ho riscontrato problemi nell’importazione del file cad, ho quindi disegnato direttamente su SAP le mensole inserendo le coordinate dei punti negli estremi.

Applichiamo ora lo stesso carico distribuito anche sulle mensole, sempre sulla proiezione di queste sull’asse X.

Applichiamo la sezione in cemento armato.

Dato che utilizziamo un carico distribuito agente sulla proiezione della struttura sull’asse orizzontale, l’inclinazione della mensola non influirà sulle reazioni vincolari (ovviamente influirà sulle sollecitazioni e  sulle deformazioni), dimostriamolo utilizzando due mensole di differenti inclinazioni ma uguale proiezione.

Il risultato della reazioni verticali sarà la somma tra q1*l e q2*b, mentre quelle orizzontali saranno uguali a 0 come immaginavamo.
In conclusione è quindi possibile eliminare le spinte orizzontali tramite alcune scelte già in fase progettuale.
 

4 ESERCITAZIONE_CENTRO DELLE RIGIDEZZE

La quarta esercitazione prevede la realizzazione di un telaio Shear - Type in calcestruzzo, formato da pilastri con sezione 40 cm x 40 cm e con travi con sezione 40 cm x 80 cm. Tale telaio è caratterizzato dalla presenza di travi infinitamente rigide che hanno un momento d’inerzia molto più grande di quello dei pilastri, ragion per cui in questo modello teorico le travi non si deformano assialmente, ma traslano cioè subiscono uno spostamento rigido, mentre i pilastri si deformano in quanto soggetti a flessione.

Il telaio che si è voluto rappresentare è caratterizzato anche dalla presenza di controventi, vincoli semplici, che si possono rappresentare come molle e che indicano la rigidezza del telaio stesso, come si può osservare nella Figura 1.

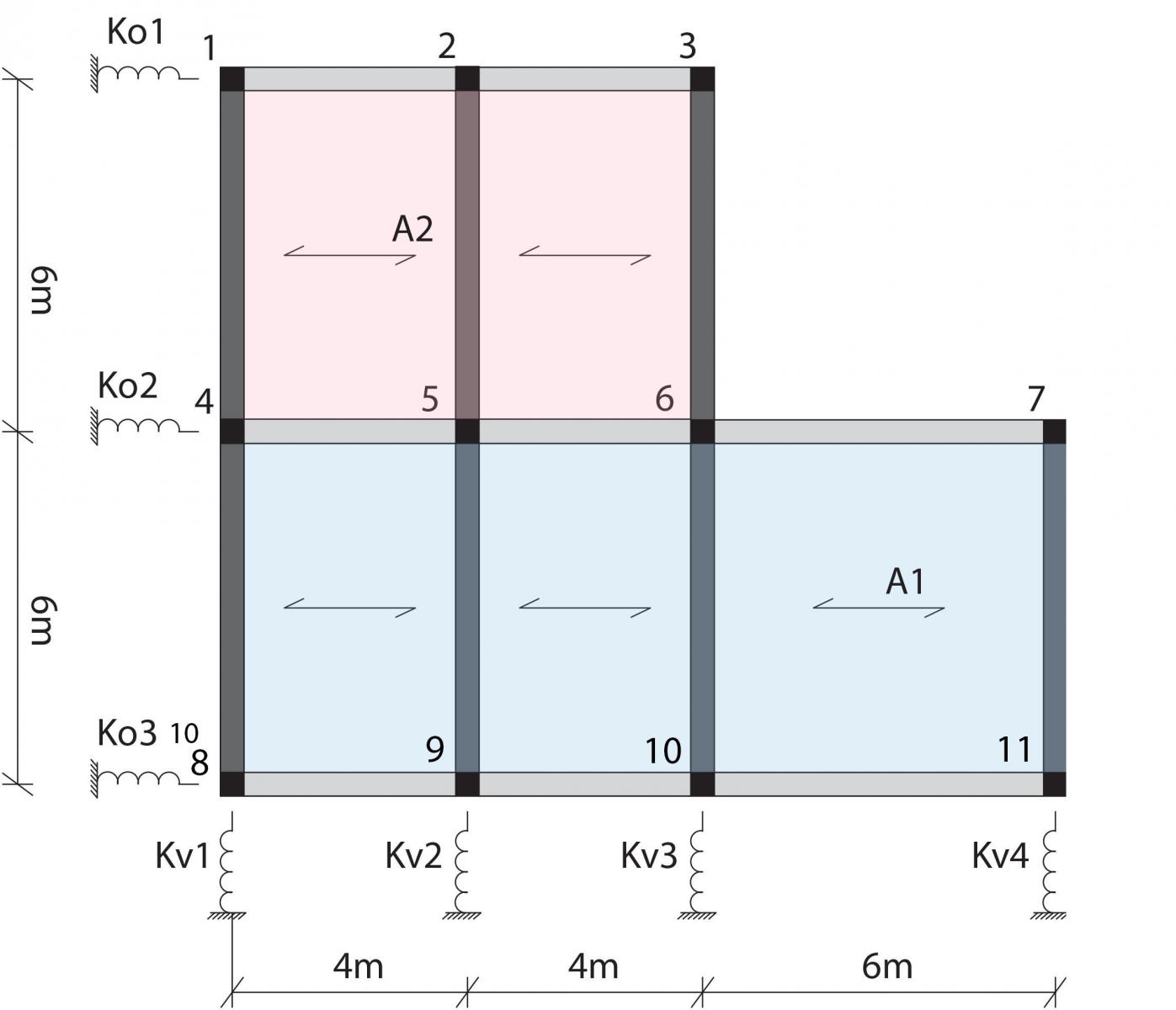
Lo scopo dell’esercitazione è quello di determinare il centro delle rigidezze di un telaio Shear – Type, per fare ciò ci si giova del supporto di un foglio di calcolo Excel. La prima fase che porta al calcolo del centro delle rigidezze prevede l’inserimento dei dati nel foglio preimpostato. Prima di tutto bisogna stabile le dimensioni del telaio e quindi anche la sua altezza, pari a 4 m.

Successivamente si procede con la compilazione del foglio Excel, che attraverso più passaggi, calcola il centro delle rigidezze.

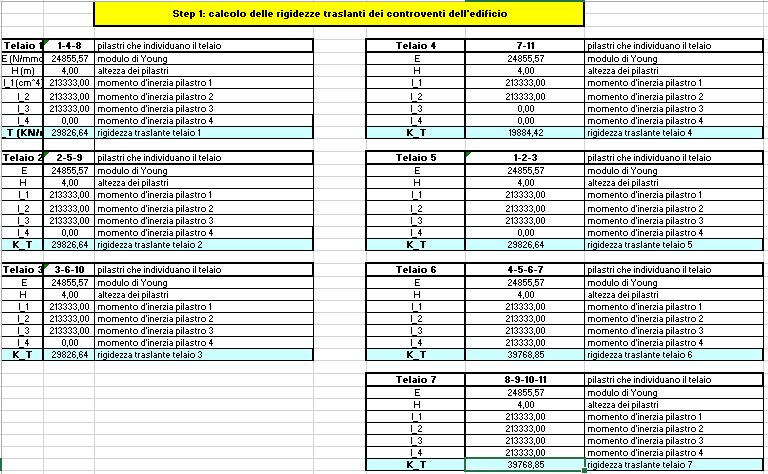
Step 1: definizione dei telai

Calcolo del modulo d’inerzia del pilastro: (bxh³) /12 = 21333 cm⁴

Modulo di elasticità del calcestruzzo: si utilizza il valore che utilizza il software SAP per una maggiore comodità di calcolo; E= 24855,57 N/mm²

Si inseriscono tutti questi dati nelle caselle del foglio Excel, compresa l’altezza dei pilastri, e si ripete la sessa operazione per tutti i telai della struttura. (Fig. 02)

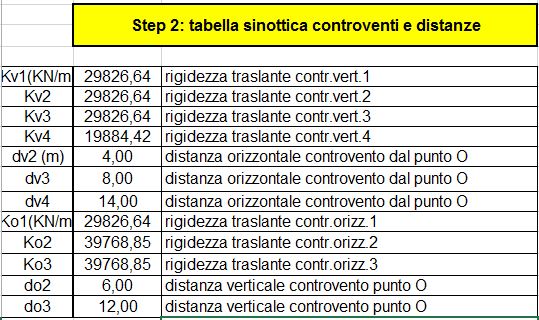
Step 2: calcolo delle distanze dall’origine degli assi 0

Si è calcolata la distanza di ogni rigidezza (molla) dall’origine 0 e si sono riportate tali misure nel foglio Excel (Fig. 03)

 

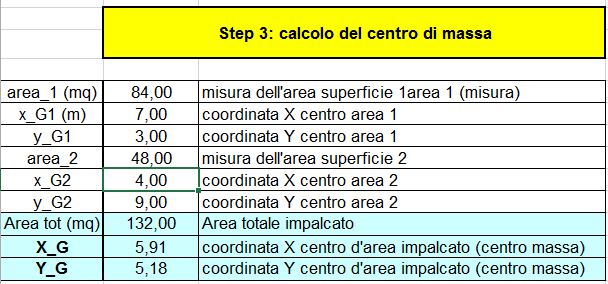
Step 3: calcolo delle coordinate del centro delle masse

Si è diviso il telaio in due parti, di cui si è successivamente calcolata l‘area, poi per ogni area si è inserita la coordinata X e la coordinata Y del centro di ognuna delle due aree. Dopo aver inserito tali dati si sono ottenute le coordinate del centro delle masse dell’intero telaio X= 5,91  Y= 5,18 (Fig. 03)

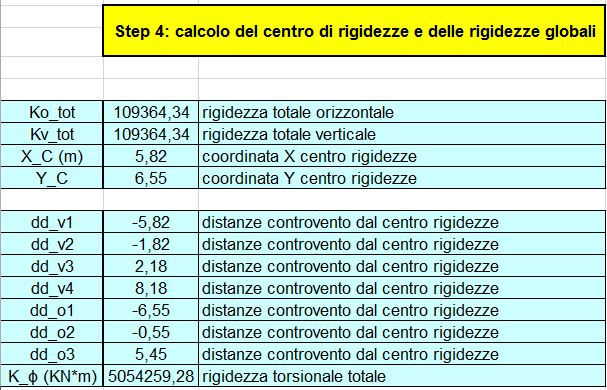
Step 4: Calcolo del centro delle rigidezze

Coordinate del centro delle rigidezze:  X= 5,82  Y= 6,55 (Fig. 04)

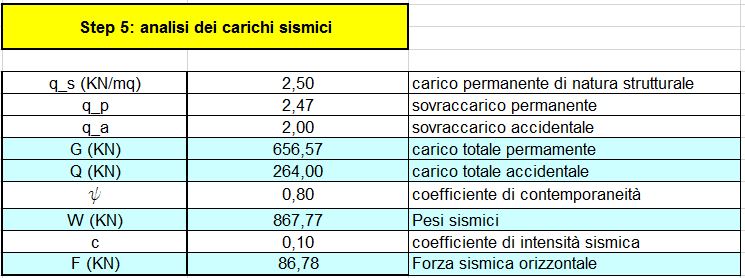
Step 5: analisi dei carichi sismici

Si ipotizza che il telaio in esame sia sottoposto ad una forza orizzontale come la forza sismica.

Si inseriscono i carichi di un solaio in calcestruzzo, ripresi dall’esercitazione precedente: qs= 2,50 KN/mq, qp= 2,47 KN/mq, qa= 2 KN/mq (Fig. 05)

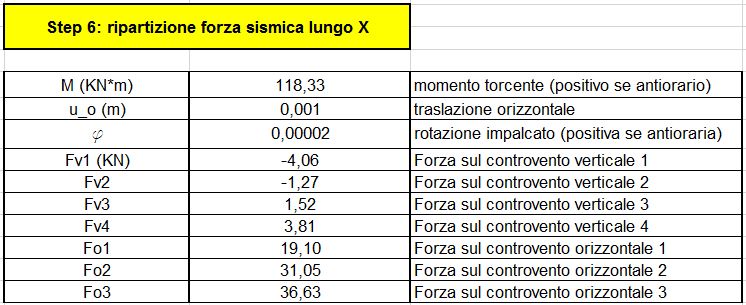
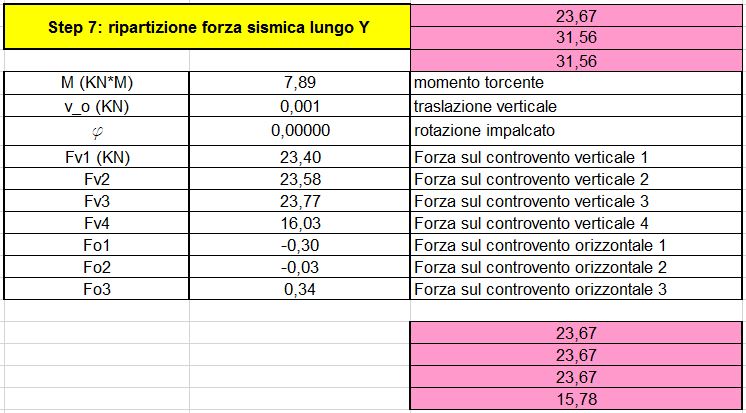
Step 6  e Step 7: ripartizione della forza sismica lungo X e lungo Y

Si sono ottenute tutte le forze cui sono sottoposti tuti i controventi. (Fig. 06, Fig. 07)

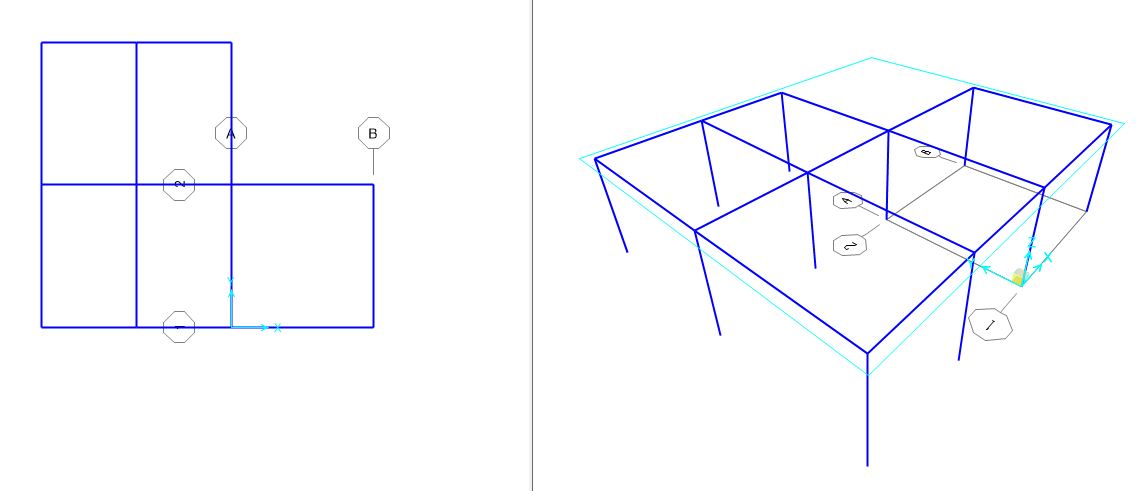
Successivamente si disegna il telaio rappresentato nella carpenteria iniziale in SAP.  (Fig. 08)

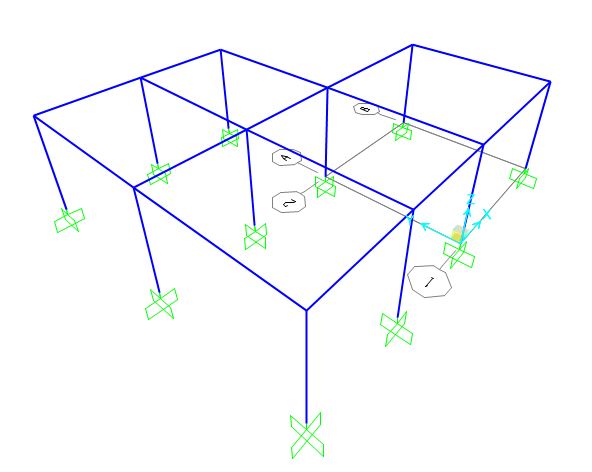
Si determinano i vincoli (incastri) alla base dei pilastri (Fig. 09) 

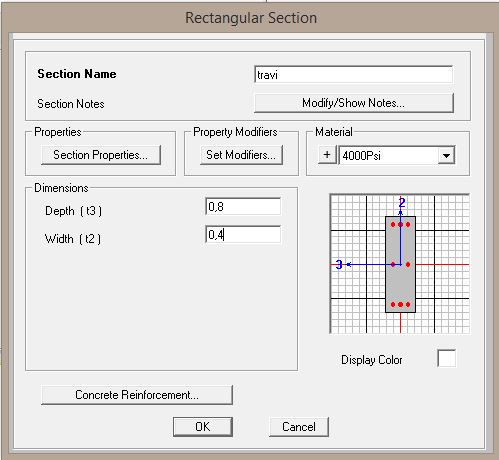
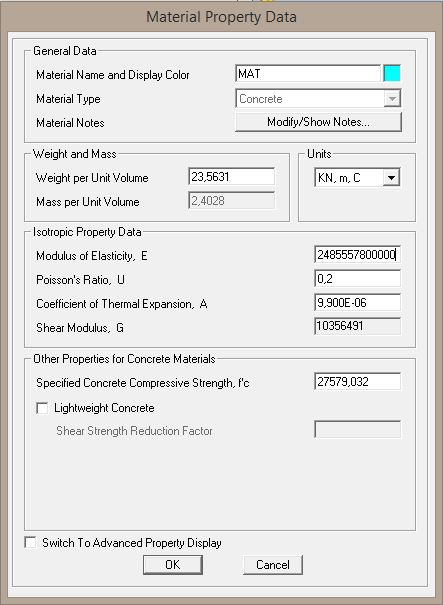
Si assegna la sezione alle travi: travi 0,4x0,80 m. Tali travi devono essere infinitamente rigide perché facciano parte di un telaio Shear – Type, per cui si aumenta esponenzialmente il modulo di elasticità E del calcestruzzo. (Fig. 10, Fig.11)

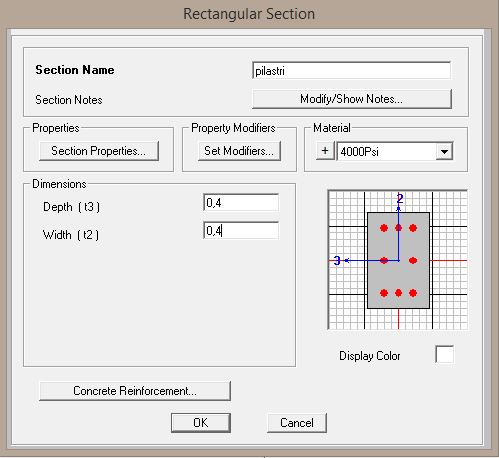
Si determina la sezione dei pilastri: pilastri 0,4x0,4 m  (Fig. 12)

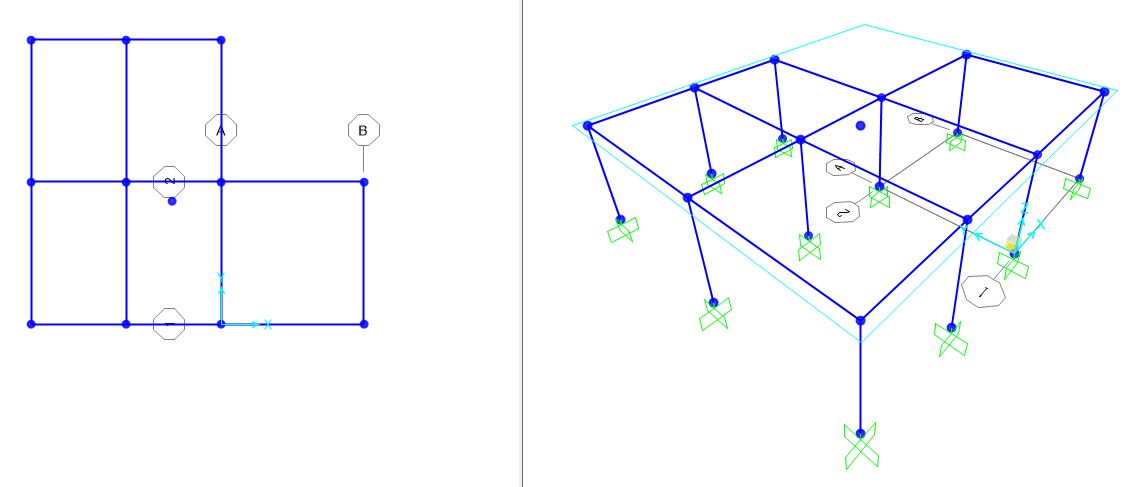
Si disegna il punto che rappresenta il centro delle masse di coordinate X= 5,91 Y= 5,18  (Fig. 13)

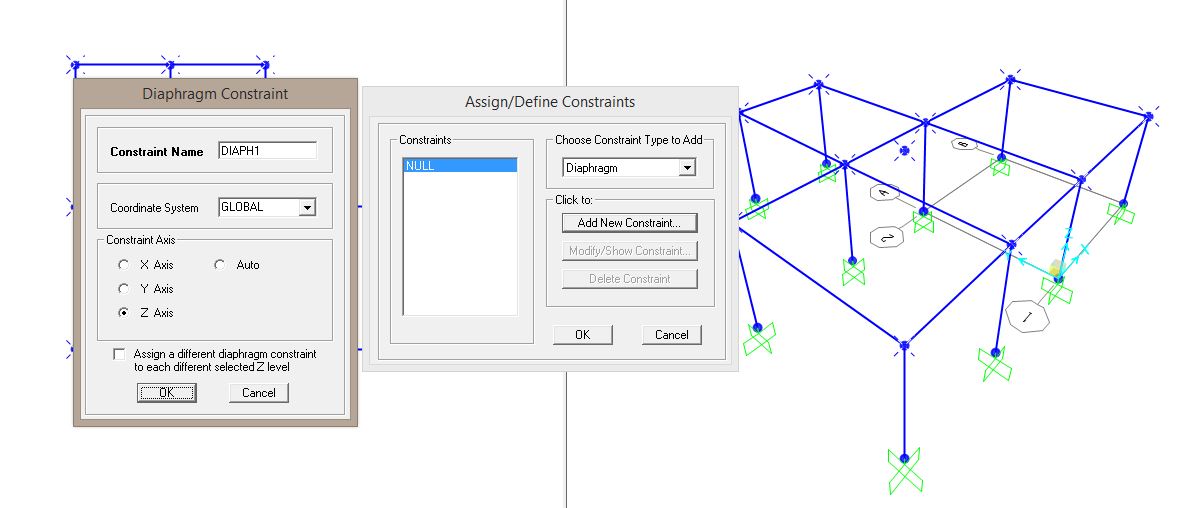
Si stabilisce che l’impalcato sia infinitamente rigido e che tutti i punti appartengano all’impalcato stesso: si selezionano tutti i punti poi si procede con il comando Assign – Joints – Constraint, si apre una  finestra e si seleziona la voce Diaphragm in modo tale da avere un telaio infinitamente rigido e sottoposto solo a traslazione.  (Fig. 14)

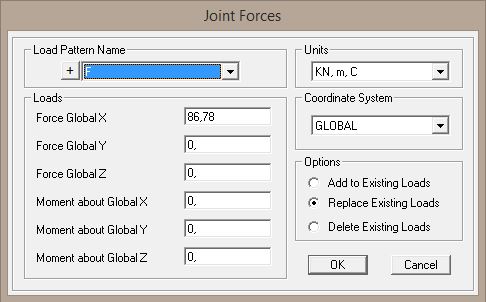
Si applica al punto la forza orizzontale (forza sismica) calcolata grazie al foglio Excel F= 86,78 KN  (Fig. 15)

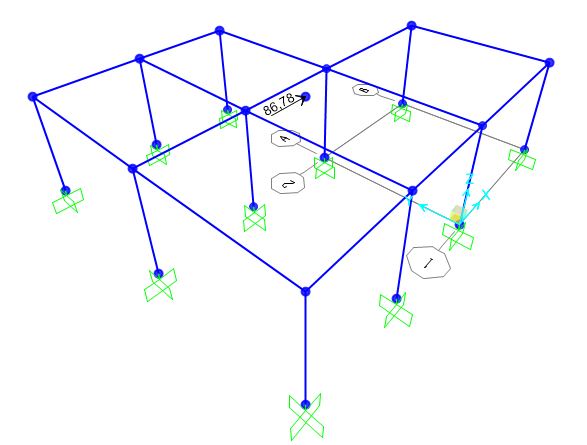
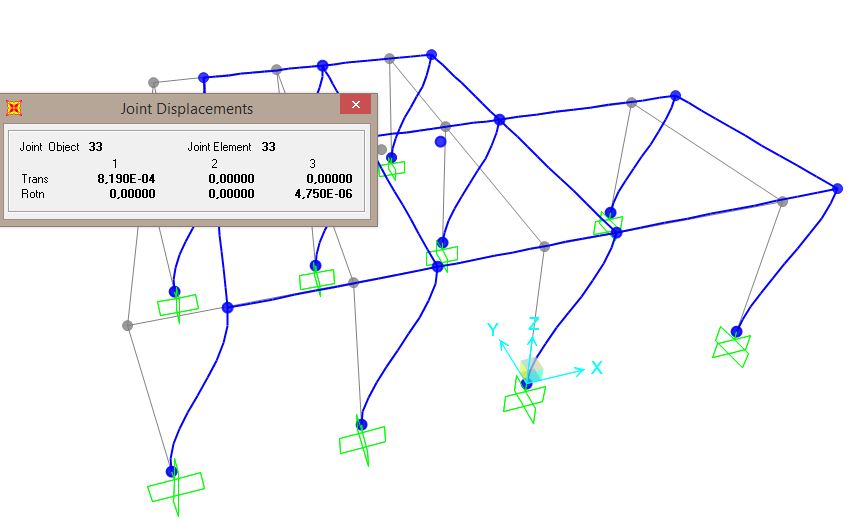
Si avvia l’analisi ottenendo una deformata che è quella caratteristica del Telaio Shear – Type.  (Fig. 16, Fig. 17)

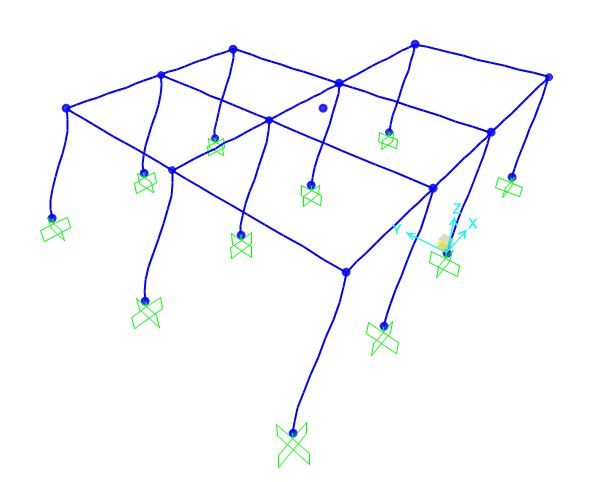
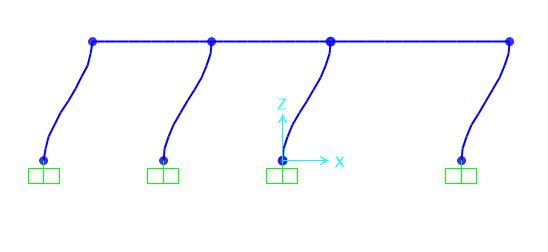
Dall’analisi si può evincere come l’impalcato trasli a causa della forza sismica, ma esso subisce anche una piccolissima traslazione che si può considerare trascurabile in quanto il centro di massa non coincide con quello delle rigidezze:  X= 5,82  Y= 6,55    (Fig. 18) 

ARCO RIBASSATO SOTTOPOSTO AD UN CARICO DISTRIBUITO

 

Disegno un arco ribassato con diametro 6m su Autocad 3d in dxf.

Una volta importato su SAP gli applico due cerniere all’imposta dell’arco e una cerniera interna in chiave per rendere la struttura isostatica.

Definisco la sezione dell’arco (40x30) e gli applico un carico distribuito da 10KNm, come nel caso dell’arco a tutto sesto.

Immagine della deformata.

Componenti della normale

ARCO A TUTTO SESTO SOTTOPOSTO AD UN CARICO DISTRIBUITO

Disegno un arco a tutto sesto con diametro 6m su Autocad 3d, lo farò in dxf per poterlo poi importare su SAP.

 

Una volta visualizzato su SAP applico due cerniere all’imposto dell’arco e una cerniera interna in chiave per rendere la struttura isostatica.

 

Definisco la sezione dell’arco (40x30) e gli applico un carico distribuito da 10KNm .

Immagine della deformata.

Componenti della normale

 

Esercizio per comprendere il comportamento di un controvento rappresentato da un telaio sottoposto a forze verticali e orizzontali. Solaio con 4 impalcati orizzontali e 8 verticali, l’edificio è in cemento armato e cerchiamo di calcolare il centro della rigidezza.

 

Modulo di elasticità E= 2,1 * 10⁵  N/mmq

Altezza dei pilastri H = 3.30 m

Esercizio per comprendere il comportamento di un controvento rappresentato da un telaio sottoposto a forze verticali e orizzontali. Solaio con 4 impalcati orizzontali e 8 verticali, l’edificio è in cemento armato e cerchiamo di calcolare il centro della rigidezza.

 

Modulo di elasticità E= 2,1 * 10⁵  N/mmq

Altezza dei pilastri H = 3.30 m

 

 

Le reazioni orizzontali vengono disegnate con una molla (avatar) che rappresenta la rigidezza del telaio.

 

Step 1

Calcolo di:

Momento di inerzia dei pilastri I  = b * h ³/ 12 =67500 cm⁴

Rigidezza traslante di ogni singolo telaio K_T =  12 * E * (I_n + I_m + I_w + I_k ) / H³ * 10 ^-5

Il calcolo delle distanze viene fatto sempre in relazione gli assi X, Y a al punto di origine O.

 

 

 

Step 2

Calcolo di:

Rigidezza traslante dei controventi orizzontali Ko

Distanza verticale dei controventi dal punto O

Rigidezza traslante dei controventi verticali  Kv

Distanza orizzontale dei controventi dal punto O

 

 

Per il calcolo del centro di massa abbiamo semplificato la struttura in tre superfici più semplici e ne abbiamo calcolati i rispettivi centri di massa. Il calcolo prevede la misurazione dell’area e delle coordinate X, Y di ogni centro dell’area delle superfici.

Step 3

Calcoli di:

Coordinate x ed y di G₁, G₂, G₃.

 

Aree parziali e totale:

Area1 = 110,595 mq

Area2 = 108,225 mq

Area3 = 110,595 mq

Area tot = 326,59 mq

Coordinate generali  del centro dell’area dell’impalcato G:

XG = 8,44 m

Y G= 9,43 m

 

 

 

Step 4

Calcolo di:

Rigidezza totale orizzontale e verticale = sommatoria delle rispettive rigidezze traslanti

Distanze dei controventi dal centro di rigidezza  (ddv_n)

Distanze dei controventi dal centro di rigidezza  (ddo_n)

Coordinate X e Y del centro delle rigidezze

Rigidezza torsionale totale  K_ϕ  =  Kv₁ * ddv₁²  + … + Kv_n * ddv_n²  + … +  Ko₁ * ddo₁²  + … + Ko_n * ddo_n²  (KN*m)

 

 

 

Scegliamo il valore dei differenti carichi (con natura strutturale permanente e accidentale) da cui deriveranno i carichi totali, ripartiti sull’area totale della struttura.

Step 5

Coefficiente di contemporaneità ψ= 0,8

Coefficiente di intensità sismica c = 0,1

 

 

Step 6 – Step 7

Momento torcente M X = c * coordinate del centro delle rigidezze

Momento torcente M Y = c * coordinate del centro dell’area dell’impalcato G

Traslazione orizzontale u = c / Ko tot

Traslazione verticale v = c / Kv tot

Rotazione impalcato ϕ = M / K_ϕ

Forza del controvento verticale Fv_n = Kv_n * ( v + ddv_n * ϕ )

Forza del controvento orizzontale Fo_n = Ko_n * ddo_n * ϕ

 

Forza del controvento verticale Fv_n = Kv_n *ddv_n * ϕ

Forza del controvento orizzontale Fo_n = Ko_n * ( u + ddo_n * ϕ )

 

Queste sono le immagini dei passaggi su SAP per creare un impalcato SHEAR TYPE:

1. Creo l’impalcato con le dimensioni e le direzioni di quello che ho studiato su exel

2.Applico degli incastri alle basi dei pilastri

3. Definisco la sezione di pilastri e delle travi Shear

4. Aumento il modulo di elasticità affinché le travi siano Shear type, modificando le proprietà del materiale dell'acciaio

 

5. Rendo rigida la struttura del solaio unendo tutti i punti e il centro di massa e con Diaphragm

6. Applico la forza in direzione X nel centro delle rigidezze

7. Movimento di un impalcato con solaio Shear Type

8. Nel caso avessimo applicato la forza nel centro dei massa

Analizziamo il comportamento di un arco a tre cerniere soggetto a carico uniformemente distribuito, nel caso di arco a tutto sesto, arco ribassato e arco parabolico, considerando per ognuno la stessa luce, pari a 6m, e facendo variare la forma e la freccia.

Bisogna ricordare, nel momento in cui avvieremo l’analisi che l’arco, essendo una struttura spingente lavora per forma e non per massa, e che pertanto proprio grazie alla propria curvatura riesce a lavorare quasi esclusivamente a sforzo normale, trasformando quindi la flessione prodotta dal carico agente su di esso. Per tale motivo l’arco a tre cerniere, una delle tre strutture isostatiche per eccellenza insieme alla trave appoggiata e alla mensola, è una struttura che ottimizza il materiale, consentendo quindi di coprire grandi luci coinvolgendo poco materiale.

Dalle analisi sui tre archi, dovrà risultare pertanto che tra gli archi circolari, quali quello a tutto sesto e quello a sesto ribassato, quest’ultimo avendo la freccia minore, ha in realtà la spinta maggiore in chiave, essendo direttamente proporzionale al rapporto luce freccia, l/f, mentre l’arco parabolico lavorerà esclusivamente a sforzo normale, per cui risulterà momento flettente e taglio nullo per ogni punto.

H= ql^2/2f

 

ARCO A TUTTO SESTO

Poiché SAP non possiede il comando linea curva, così come è difficile disegnare strutture complesse, si disegna l’arco su cad 3d, così da importarlo successivamente in SAP, ricordandosi di lavorare su un unico livello che non sia il layer 0 in quanto il programma non lo riconosce, e di salvare come un file .dxf 2004 per avere la certezza di poterlo importare.

L’arco a tutto sesto è un arco circolare con l=f=R, con R raggio della circonferenza su cui si imposta l’arco; per cui le imposte saranno sulla stessa linea e la variabile, ossia l’angolo α sarà compreso tra 0<α<π/2.

Nel momento in cui lo importiamo su SAP ricordiamoci di impostare la global up direction, ossia la direzione della forza di gravità, in direzione dell’asse z, le unità di misura del sistema KN,m,C, e il layer che vogliamo far leggere al programma.

Fatto ciò individuiamo il punto in chiave, congiungendo prima i due punti all’imposta dell’arco e poi dal midpoint di questa linea alzarne un’altra in direzione z fino al d incontrare l’arco nel suo punto di chiave.

Definiamo ora i tre punti noti come le tre cerniere dell’arco: per il punto in chiave, o meglio i due punti che lo formano, si decide di utilizzare il comando release, selezionando infatti i due vertici attraverso il percorso Assign-Frame-Releases-Partial Fixity andiamo ad indicare che il momento 33 è nullo, start per il vertice a sinistra e end per quello a destra; per i punti d’imposta andiamo invece ad indicare che sono delle cerniere attraverso il comando vincolo esterno Restraints

Si assegna ora la sezione all’arco, in quanto non essendo stato disegnato su SAP, il programma non lo considera tale e non avvierebbe l’analisi successivamente

E infine si assegna un carico uniformemente distribuito, pari per ogni arco a 10KN.

Infine avviamo l’analisi e apprezzare la deformata dovuta al all’azione del carico.

Possiamo infine controllare le reazioni vincolari nelle cerniere all’imposta, notando che la reazione verticale nella cerniera d’imposta sarà proprio pari a ql= 30 KN, con l=3m, e la reazione orizzontale che nasce per equilibrare l aspinta in chiave pari a ql^2/2f= 15 KN

Infine apprezziamo i diagrammi dello sforzo assiale e dei momenti

ARCO RIBASSATO

Analizziamo ora un arco ribassato soggetto alle stesse condizioni del precedente, per cui stessa luce e carico distribuito, per cui stesse reazioni vincolari parametricamente, ma freccia minore, da cui risulterà una spinta maggiore in chiave.

Applichiamo il carico uniformemente distribuito

ARCO PARABOLICO

Infine operiamo lo stesso procedimento anche per l’arco parabolico, da cui noteremo la spinta sempre minore rispetto all’arco ribassato, è un arco funicolare che riesce quindi a trasformare completamente la flessione dovuta ai carichi agenti in sforzo normale ed ad azzerare il taglio e il momento.

Definiamo un impalcato ad un piano e studiamone il comportamento a seguito dell'azione di una forza sismica. 

Indichiamo con Kv i controventi verticali e con Ko i controventi orizzontali.

Utilizzando un foglio di calcolo Excel ricaviamo le rigidezze traslanti di ogni controvento. Trattandosi di telai Shear-Type la rigidezza è calcolata con la formula [12E(I1+I2+I3+...+In)]/h3  dove E è il modulo di elasticità del materiale, (I1+I2+I3+...+In) è la somma dei momenti d'inerzia dei pilastri che compongono il controvento e h è l'altezza dei pilastri.

La seguente è una tabella di riepilogo che servirà per calcolare la posizione del centro delle rigidezze, ovvero il punto in cui si concentra la reazione dell'impalcato.

Dividendo l'impalcato in aree semplici possiamo calcolare la posizione del centro delle masse, ovvero il punto di applicazione delle forze esterne. Le coordinate del centro delle masse si trovano con le seguenti formule

XG= [A1Xg1 + A2Xg2 + A3Xg3]/Atot                 YG = [A1Yg1 + A2Yg2 + A3Yg3]/Atot

Calcoliamo la posizione del centro delle rigidezze facendo riferimento alla "tabella di riepilogo" utilizzando formule simili a quelle per il calcolo del centro delle masse

Xc = [Kv2dv2 + Kv3dv3 + Kv4dv4]/Ktot                 Yc = [Ko2do2 + Ko3do3 + Ko4do4]/Ktot

Procediamo con l'analisi dei carichi per ricavare la forza sismica orizzontale da applicare al centro delle masse. I pesi sismici sono la somma del carico totale permanente e il carico totale accidentale, quest'ultimo è ridotto dal coefficiente di contemporaneità che tiene conto delle poche probabilità che azioni diverse accadano contemporaneamente. Il peso sismico viene poi moltiplicato per un coefficiente di intensità sismica proprio della zona in cui ci troviamo.

Ricaviamo, infine, come sono ripartite le forze lungo X, Y e sui controventi orizzontali e verticali.

Verifichiamo la struttura su SAP

Modelliamo la struttura su SAP osservando i seguenti passaggi:

• assegnare alla base dei pilastri il vincolo "incastro"
• definire il centro delle masse e il centro delle rigidezze utilizzando le coordinate ricavate dal foglio Excel
• assegnare il vincolo interno "Diaphragm" a tutti i punti superiori dell'impalcato compresi il centro delle masse e il centro delle rigidezze (in questo modo facciamo si che tutti i punti si comportino come un unico oggetto) 
• assegnare la sezione rettangolare ai pilastri tenendo conto dell'orientamento di ognuno di essi
• assegnare la sezione delle travi

In SAP non è prevista la possibilità di definire un telaio Shear-Type poichè è un modello teorico. Rendiamo le travi degli elementi infinitamente rigidi aumentando di molto il loro momento d'inerzia per avere un comportamento che approssimi il più possibile quello del telaio Shear-Type.

Definiamo un nuovo caso di carico (trascurando il peso proprio) e assegniamo la forza sismica in direzione Y di intensità 67,20 Kn (come ricavato dal foglio Excel).

Avviamo l'analisi. Ci aspettiamo che l'impalcato ruoti dato che il centro delle masse e il centro delle rigidezze non coincidono.

Dalla deformata sulla destra possiamo notare come il modello creato in SAP approssimi bene il comportamento di un telaio Shear-Type. 

Analizzando gli spostamenti del centro delle rigidezze notiamo una rotazione trascurabile dato che lo spostamento massimo è di 4 decimi di millimetro in direzione Y. 

Per evitare che l'impalcato ruoti dovremmo intervenire irrigidendo i plastri nella zona sinistra, cercando di far coincidere (o avvicinare il più possibilie) il centro delle rigidezze al centro delle masse.

cari ragazzi,

in allegato il programma del corso di quest'anno.

Buono studio

la prof.