SdC(b) (LM PA)

 

In riferimento allo schema strutturale di carpenteria di sopra verifichiamo che l'abbassamento della trave che sostiene lo sbalzo del solaio rientri nel rapporto: abbassamento<luce dello sbalzo/250. Nelle diverse tecnologie già studiate di Legno Lamellare, Acciaio, Cemento Armato.

Il foglio excell realizzato per la verifica richiede l'inserimento dei seguenti dati: interasse tra le travi portanti, luce dello sbalzo, carico strutturale, carico portato, carico accidentale. E la definizione dell'altezza ingegnerizzata della trave, il foglio excell a questo punto calcola il peso proprio della trave e lo somma ai carichi di sopra.

Il rapporto abbassamento<luce dello sbalzo/250 è verificato.

 

Il foglio excell realizzato per la verifica richiede l'inserimento dei seguenti dati: interasse tra le travi portanti, luce dello sbalzo, carico strutturale, carico portato, carico accidentale. E la definizione dell'altezza ingegnerizzata della trave, il foglio excell a questo punto calcola il peso proprio della trave e lo somma ai carichi di sopra.

 

Il rapporto abbassamento<luce dello sbalzo/250 è verificato.

 

Il foglio excell realizzato per la verifica richiede l'inserimento dei seguenti dati: interasse tra le travi portanti, luce dello sbalzo, carico strutturale, carico portato, carico accidentale. E la definizione dell'altezza ingegnerizzata della trave, il foglio excell a questo punto calcola il peso proprio della trave e lo somma ai carichi di sopra.

Il rapporto abbassamento<luce dello sbalzo/250 è verificato.

 

 

 

 

 

 

Andiamo a calcolare il centro delle rigidezze di un impalcato in cemento armato avente 5 telai verticali e 3 orizzontali.
Tale tipo di studio ci porterà a capire meglio il funzionamento di telai non solo sottoposti ad azioni verticali.  Infatti, un telaio, se ben pensato in fase progettuale, può resistere anche alle azioni orizzontali a cui la struttura è sottoposta, quindi agire da vero e proprio controvento.

Disegniamo ora le rigidezze (Kv e Ko) dei singoli telai. Per essere rappresentate useremo un avatar, una molla, che meglio raffigura la reazione alle spinte orizzontali di questi controventi.
Aggiungiamo anche gli assi X e Y, dato che ci servirà un punto di origine su cui fare calcoli di natura geometrica.

Procediamo ora su Excel.
Tramite questo algoritmo è possibile calcolare centro di massa, centro delle rigidezze e ripartizioni delle forze sismiche.
Primo passo, calcolare la rigidezza di ogni singolo controvento. Per fare ciò, necessitiamo modulo di Young (a seconda del materiale), momento di inerzia (che ovviamente varierà in caso vari la sezione) di ogni pilastro, e altezza.
Per il momento di inerzia, data la forma quadrata del pilastro, useremo la formula b^4/12 (b*h^3/12 con h e b uguali).
Dato che il nostro telaio è di tipo Shear-Type la struttura orizzontale è infinitamente rigida e quindi indeformabile assialmente mentre i pilastri sono soggetti a flessione. La trave perciò si muoverà con atto di moto rigido. Dato l’incastro dei pilastri a terra quindi, gli unici spostamenti saranno nella testa del pilastro, e uguali per tutti i pilastri che compongono il singolo telaio. La rigidezza traslante (K) quindi sarà calcolata come:
K=12*E*Itot/h^3

Telai verticali:

Telai orizzontali:

Elenchiamo ora le distanze orizzontali e verticali dei singoli controventi rispetto all’origine:

Suddividiamo ora l’impalcato in figure geometriche semplici di cui possiamo trovare i centri di massa:

Possiamo ora trovare il centro di massa dell’intera struttura. Le coordinate di tale centro possono essere trovate come sommatoria delle distanze dei singoli centri di massa rispetto agli assi (y o x a seconda di ciò che si vuole calcolare) moltiplicate per le rispettive aree e dividendo il totale per l’area complessiva.
Gmx=∑xG*Ai/Atot
Gmy=∑yG*Ai/Atot

Calcoliamo ora le coordinate del centro di rigidezza, e le distanze di ogni singolo controvento da queste.
Per trovare le coordinate procederemo allo stesso modo, calcolando cioè la sommatoria del prodotto fra le rigidezze di ogni controvento per le rispettive distanze (verticali o orizzontali a seconda della coordinata da trovare) il totale diviso la rigidezza verticale o orizzontale totale.
Grx=∑Kvi*dvi/Kvtot
Gry=∑Koi*doi/Kotot

Infine troviamo la rigidezza torsionale totale:

Dalla somma dei carichi strutturali, permanenti e accidentali della struttura (qs, qp e qa), calcoliamo i carichi sismici e ripartiamoli lungo gli assi X e Y per ogni controvento.

Ripartizione forza sismica lungo X:

Ripartizione forza sismica lungo Y:

Procediamo ora importando l’impalcato su SAP e incastriamo tutti i pilastri a terra:

Assegniamo ad ogni pilastro la sua sezione/materiale (assign/frame/frame section), utilizzando la nostra sezione 30x30 in Concrete.

Stesso procedimento con le travi, ma di sezione 30x60:

Disegniamo ora il centro delle rigidezze precedentemente calcolato:

Rendiamo rigida la struttura, comprensiva del centro di rigidezze, in modo tale da far spostare tutto insieme, anche se il punto è esterno.
Per fare ciò selezioniamo tutti i nodi trave/pilastro e il centro delle rigidezze, andiamo su Assign/Joint/Constraint e selezioniamo Diaphragm.

Dato che come abbiamo detto, stiamo usando un telaio Shear-Type, dobbiamo rendere indeformabili le travi. Per farlo possiamo andare su Frame Property e inserire un momento di inerzia molto alto.

Selezioniamo ora il centro delle rigidezze e applichiamo la forza sismica lungo l’asse X del valore calcolato con l’algoritmo di Excel.

Andiamo a calcolare la deformazione:

Possiamo notare come il centro delle rigidezze non venga sottoposto a rotazione ma solo a traslazione:

Andiamo infine a calcolare rispettivamente il momento 2-2 e il momento 3-3 della struttura.

 

CALCOLO DEL CENTRO DI RIGIDEZZA IN UN IMPALCATO CON TELAIO SHEAR-TYPE

Analisi del comportamento di un impalcato sollecitato da forze esterne orizzontali e del comportamento dei controventi nel rispondere a tali sollecitazioni.
I controventi vengono rappresentati come delle molle, in quanto rappresentano dei vincoli elastici, cioè in grado di rispondere alle forze esterne subendo una deformazione reversibile.
La capacità di queste molle di rispondere alle forze esterne sarà strettamente collegata alla loro rigidezza k e alla loro distanza dal CENTRO DELLE RIGIDEZZE, unico punto in cui la risultante delle forze esterne applicate avrà momento pari a zero e dunque rotazione nulla.
Dunque una volta determinate le caratteristiche dimensionali e tipologiche dell’ impalcato e il materiale dei suoi elementi, attraverso un file excel si calcolerà il CENTRO DELLE RIGIDEZZE.

Scelgo di analizzare il seguente impalcato in calcestruzzo:

  

H PILASTRI: 4,00 m
PILASTRI IN CEMENTO ARMATO __ MODULO DI YOUNG : E= 21000 Nmm
SEZIONE PILASTRI:  30 x 50 cm

A seconda dell’ orditura del telaio avremo i pilastri orientati in 2 diversi modi e di conseguenza con diversi MOMENTI DI INERZIA.

Prima di procedere con i calcoli su excel definisco la suddivisione dei telai con le rispettive numerazioni dei pilastri di un determinato pilastro, a seconda che io stia analizzando l’impalcato rispetto ai controventamenti lungo l’asse x e poi lungo l’asse y.
TELAIO VERTICALE____ LUNGO Y-Z                                 TELAIO ORIZZONTALE____LUNGO X-Z       
                                   
TELAIO 1 _ PILASTRI 1-5                                                  TELAIO 5 _ PILASTRI 1-2-3-4
TELAIO 2 _ PILASTRI 2-6                                                  TELAIO 6 _ PILASTRI 5-6-7-8
TELAIO 3 _ PILASTRI 9-7-3                                              TELAIO 7 _ PILASTRI 9-10
TELAIO 4 _ PILASTRI 10-8-4          

STEP 1 Calcolo delle RIGIDEZZE TRASLANTI dei controventi dell’edificio.
La rigidezza traslante dei controventi presi in analisi è dato dalla somma delle rigidezze di ciascun pilastro.
                                        

STEP 2     Tabella sinottica dei controventi e delle loro distanze dell’origine
Ci permette di raccogliere dati sulle rigidezze traslanti prima ottenute e sulle loro distanze rispetto al centro 0, le quali dipendono dagli interassi e dalle luci tra i pilastri. 

STEP 3      Calcolo del CENTRO DELLE MASSE

Conviene suddividere la pianta dell’ impalcato in aree geometriche regolari per determinarne facilmente il BARICENTRO.

STEP 4  Calcolo del CENTRO DELLE RIGIDEZZE e delle RIGIDEZZE GLOBALI:
Sommo le rigidezze verticali e poi le rigidezze orizzontali;
Trovo la rigidezza totale orizzontale e verticale e faccio una media ponderata tra le due;
Per il CENTRO DELLE RIGIDEZZE calcolo, per ogni molla, la sua rigidezza per il suo braccio (distanza dal punto considerato come origine);
Sommo tutti i prodotti ottenuti nelle due direzioni e li divido per la rigidezza globale
Noto il centro delle rigidezze C calcolo la distanza di ogni telaio da esso. 
Calcolo la RIGIDEZZA ROTAZIONALE K che è data dalla somma dei prodotti de
Ora che il centro delle rigidezze è noto possiamo calcolare la distanza di ogni telaio da C; non rimane ora che calcolare la RIGIDEZZA ROTAZIONALE K che è data dalla sommatoria dei prodotti delle rigidezze traslanti di ciascun telaio per la distanza al quadrato di ognuno di essi rispetto a C.

STEP 5 Analisi dei carichi sismici:
Successivamente, dopo aver individuato il carico q del solaio (ricordando che q =qp + qs + qa), lo moltiplico per il coefficiente di contemporaneità per ottenere i pesi sismici. Tali pesi vengono moltiplicati per il coefficiente di intensità sismica, per ricavarne il valore dell’ipotetica forza sismica agente (premettendo che tale valore è comunque imprevedibile. Infatti il coefficiente di intensità sismica ha un valore molto elevato).

STEP 6 e 7: Ripartizione della forza sismica lungo X e Y:

Individuo come l’ipotetica forza sismica si ripartisce nelle due direzioni. Nel mio caso il centro delle rigidezze e il centro delle masse NON coincidono, pertanto avrò una rotazione data dalla forza moltiblicata per il braccio, il cui valore coincide con la differenza tra il centro delle masse e il centro delle rigidezze, rispettivamente all’ asse x e all’ asse y.

Il foglio di calcolo trova automaticamente la traslazione orizzontale Ux e la traslazione verticale Uy, la rotazione dell’ impalcato. Con questi dati è possibile calcolare ulteriormente come si ripartisce la forza sismica su ciascuna molla. 
Moltiplico la rigidezza della molla per la somma tra lo spostamento (ad essa perpendicolare) ed il prodotto tra rotazione e distanza dal centro delle rigidezze. 
Ricavo infine le reazioni con cui ciascuna molla reagisce e contrasta la forza orizzontale sismica in ordine di numerazione da ko1 a ko3 su x, da kv1 a kv4 su y.

Ora su SAP rifaccio la struttura sopra analizzata e imposto la forza del sisma sul centro delle rigidezze calcolato precedentemente. Verifico così la corrispondenza dei valori e soprattutto che la deformazione subita dall'impalcato sia la sola traslazione ma non la rotazione.

Importiamo la struttura da Rhino su SAP

Selezioniamo tutti i nodi a terra di tutti i pilastri e assegnamo gli incastri a terra.  (Assign -> Joint -> Restraints)

A questo punto selezioniamo prima i pilastri e poi le travi e ne definiamo la sezione e il materiale (calcestruzzo).

Per quanto riguarda i pilastri dobbiamo fare attenzione a selezionare quelli disposti in orizzontale e assegnarli una sezione di 30x50, e a quelli in verticale una sezione 50x30.

(Assign -> Frame -> Frame Section -> dal menù a tendina seleziono  “CONCRETE")

Per aumentare la rigidezza delle travi ed assimilarle al modello di telaio SHEAR-TYPE, infinitamente rigido:

Assign -> Frame -> Property Modifiers -> Aumento il Momento d' Inerzia

A questo punto imposto il CENTRO DELLE RIGIDEZZE secondo le coordinate calcolate dal foglio di calcolo (X=13,69 ; Y=6,75).

Successivamente applichiamo la forza sismica orizzontale nel centro delle rigidezze.             

 

Prima di procedere con l'analisi imposto seleziono tutti i nodi, compreso il punto in cui è impostata l'azione sismica, e assegno il Diaphragm Constraint.

A questo punto avvio l' analisi. 

 

Vediamo i diagrammi e i valori del Momento 33.

                     

 

                              

 

 

L’orditura del solaio considerato (edificio ad uso residenziale) prevede travi appoggiate e uno sbalzo di 3 metri; verrà dimensionata la mensola utilizzando un foglio di calcolo excel, effettuando la verifica a deformabilità della trave. Verranno considerate tre diverse tipologie di solaio, con tecnologia in legno, c.a. e acciaio. Molto importante, così come per la trave su appoggi, sarà la luce l, in questo caso lunghezza dello sbalzo pari a 3 m, e l’interasse pari a 5 m.

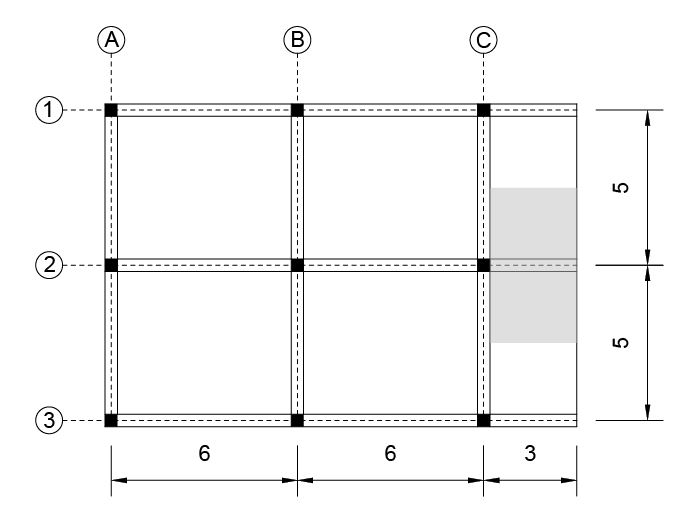
La composizione dei solai è ripresa dall’esercitazione 2 sulla trave appoggiata.

 

SOLAIO IN LEGNO

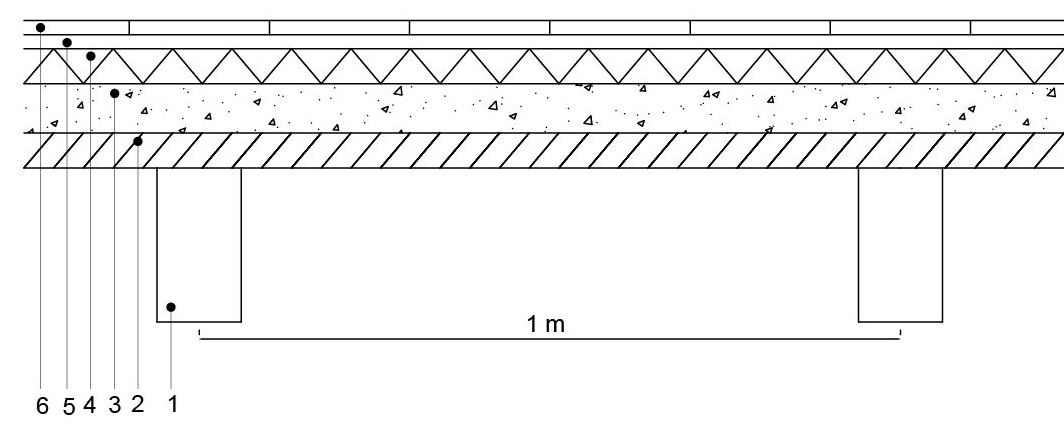
1: travetto                                    12x22 cm

2: impalcato                                 5 cm spessore

3: cls caldana                               7 cm spessore

4: isolante                                     5 cm spessore

5: massetto di allettamento         2 cm spessore

6: parquet, listelli 20x100 cm;      2 cm spessore

Si calcolano i carichi strutturali qs, accidentali qa, permanenti qp

carichi strutturali  (si esclude per ora il peso proprio della trave) qs :

-          impalcato           0,05 m * 4 kN/mc = 0,2 kN/mq

-          travetti                 1 * 0,22 m* 0,12 m * 6 kN/mc = 0,16 kN/mq                  

 qs = 0,36 kN/mq

carichi permanenti qp :

-          pavimento in parquet         0,02 m * 6,9 kN/mc =  0,14 kN/mq   

-          massetto in cls leggero      0,02 m * 14 kN/mc = 0,28 kN/mq

-          isolante                               0,05 m * 0,4 kN/mc = 0,02 kN/mq

-          cls caldana                          0,07 m * 24 kN/mc = 1,68 kN/mq

-          incidenza impianti              1 kN/mq     (da normativa)

-          incidenza tramezzi              0,5 kN/mq  (da normativa)                             

qp = 3,62 kN/mq

carichi accidentali qa:

-          ambiente residenziale        2,00 kN/mq                                                        

qa = 2,00 kN/mq

q = qa + qs + qp = 5,98 kN/mq

-          coefficienti di sicurezza: ogni carico va moltiplicato per un coefficiente di sicurezza

γs = 1,3 

γp = 1,3 

γA= 1,5

totale carichi = 8,17 kN/mq

Andando a moltiplicare questo valore per l’interasse si ottiene il carico che agisce sulla trave considerata.

q = 40,87 kN/m

Si imposta poi l= lunghezza dello sbalzo, ottenendo un valore del Momento massimo (ql²/2) pari a:

M = 183,92 KNm

Viene poi calcolata la resistenza di progetto, definita dal prodotto tra resistenza caratteristica del legno e il coefficiente di degrado nel tempo Kmod,  diviso per il coefficiente di sicurezza:  

σ_amm= 13,24 N/mm²

con la formula di Navier so che  σ_amm = Mmax/ Wmax

inoltre W_max = bh²/ 6 la cui formula inversa permette di calcolare la sezione impostando un valore alla base della trave b.

Viene poi inserito il valore dell’altezza h_d ingegnerizzata = 50 cm, e il valore del modulo E di elasticità che sarà 11600 N/mm²  per un legno lamellare classe GL24.

Si avrà poi il valore del modulo di inerzia I_x = bh³/12 per sezione rettangolare.

Ciò che si ottiene è infine il valore massimo dell’ abbassamento, che è uno spostamento lineare (risolto nelle strutture isostatiche con il metodo degli spostamenti).

v_max= ql⁴/8EI_x = 0,86 cm

per avere un valore di abbassamento accettabile, rispetto alla struttura in esame, esso non deve superare 1/250 della luce, quindi se  

l/ v_max ≥ 250.

Ottenendo quindi  l/ vmax = 350,40 il valore dello spostamento è accettabile.

Inserendo ora anche il peso proprio della trave calcolata si verifica infine la mensola

carichi strutturali  qs :

-          impalcato           0,05 m * 4 kN/mc = 0,2 kN/mq

-          travetti              1 * 0,22 m* 0,12 m * 6 kN/mc = 0,16 kN/mq  

-          trave                 0,5 m * 0,4 m * 3,80 kN/mc = 0,76 kN/ mq 

           valore al mq assimilabile a quello al metro lineare

dove 380 kN/ m³  è il peso specifico del legno lamellare classe GL24

 qs = 1,12 kN/mq

Inserendo il nuovo valore del carico strutturale si ottiene comunque anche considerando il peso proprio della mensola un valore ammissibile di spostamento massimo.

 

 

 

SOLAIO IN ACCIAIO

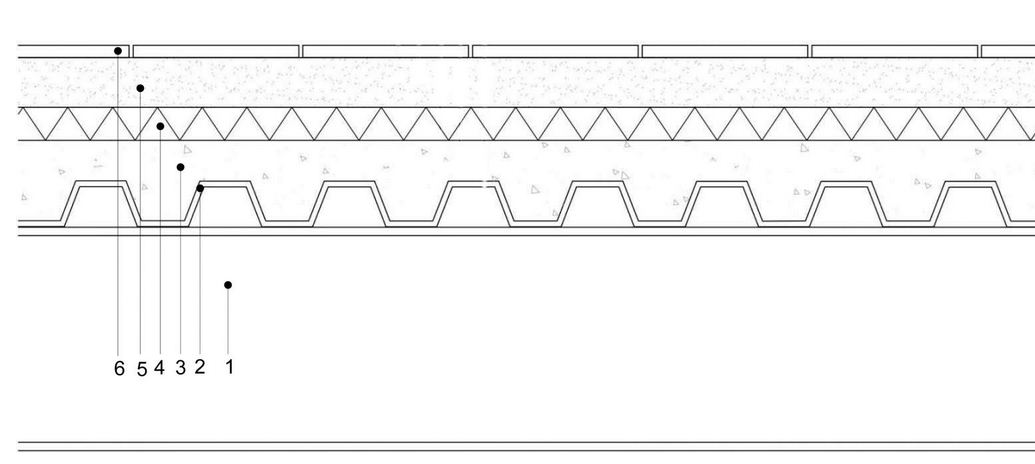
1: trave                                       

2: lamiera grecata                             6 cm spessore

3: massetto cls                                  5 cm spessore

4: isolante                                         4 cm spessore

5: massetto                                       6 cm spessore

6: pavimento gres porcellanato     1,5 cm spessore

 

carichi strutturali  (si esclude per ora il peso proprio della trave) qs :

-          massetto cls         0,11 m * 24 kN/mc = 2,64 kN/mq

-          lamiera grecata   0,24 kN/mq                                                             

qs = 2,88 kN/mq         

carichi permanenti qp :

-          pavimento in gres porcellanato 0,015 m * 20 kN/mq = 0,3 kN/mq

-          massetto in cls leggero 0,06 m * 14 kN/mc = 0,84 kN/mq

-          isolante 0,04 m * 0,4 kN/mc = 0,016 kN/mq

-          incidenza impianti 1 kN/mq

-          incidenza tramezzi 0,5 kN/mq                                                                     

qp = 2,66 kN/mq

carichi accidentali qa:

-          ambiente residenziale        2,00 kN/mq                                                        

qa = 2,00 kN/mq

Andando a moltiplicare il valore del carico totale per l’interasse si ottiene il carico che agisce sulla trave considerata.

q = 42,7 kN/m

vengono poi individuati i valori di Momento massimo, la resistenza caratteristica del materiale fd  in base alla tensione di snervamento dell’acciaio fyk, e Wx (usando la formula di Navier σamm= Mmax/ Wmax) cioè il modulo di resistenza minimo a flessione. In base a quest’ultimo valore si è scelta una trave IPE 400; l’altezza della trave sarà quindi di 40 cm, il peso = 66,3 kg/m, Ix = 23130, da cui si ottiene un carico totale (compresa la trave) di 49,33 kN/m.

L’abbassamento risulta di 1,02 cm e ammissibile rispetto alla struttura.

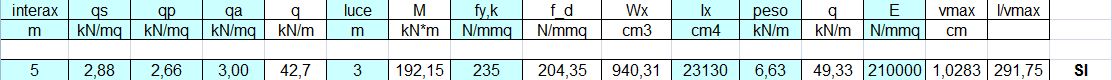
SOLAIO IN LATERO-CEMENTO

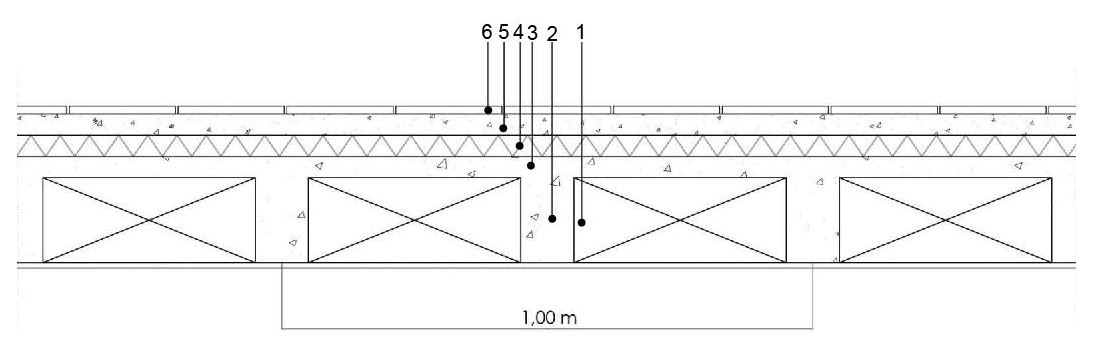
1: pignatte                                     40 x 16 cm                                      

2: travetti                                       10 x 16 cm  

3: caldana cls                                 4 cm spessore

4: isolante                                       4 cm spessore

5: massetto alleggerimento           4 cm spessore

6: pavimento gres porcellanato     1,5 cm spessore

 

carichi strutturali  (si esclude per ora il peso proprio della trave) qs :

-          caldana         0,04 m * 24 kN/mc = 0,96 kN/mq

-          travetti          2* 0,10 m * 0,16* 24 kN/mc = 0,77 kN/m

 qs = 1,73 kN/mq         

carichi permanenti qp :

-          pavimento in gres porcellanato         0,015 m * 20 kN/mq = 0,3 kN/mq

-          massetto in cls leggero           0,02 m * 14 kN/mc = 0,28 kN/mq

-          isolante                                   0,04 m * 0,4 kN/mc = 0,016 kN/mq

-          pignatte                                   2 * 0,4 m * 0,16 m * 8 kN/mc = 1,02 kN/mq

-          incidenza impianti                    1 kN/mq

-          incidenza tramezzi                  0,5 kN/mq

qp = 3,12 kN/mq

carichi accidentali qa:

-          ambiente residenziale        2,00 kN/mq                                                        

qa = 2,00 kN/mq

q = 6,85 kN/mq

-          coefficienti di sicurezza: ogni carico va moltiplicato per un coefficiente di sicurezza

γs = 1,3 

γp = 1,3 

γA= 1,5                                                                       

Andando a moltiplicare il valore del carico finale per l’interasse si ottiene il carico che agisce sulla trave considerata.

q = 46,52 kN/m

Come nei casi precedenti si ottiene il valore del momento massimo che agisce sulla sezione.

Si inseriscono nel calcolo le resistenze dei materiali: acciaio di armatura e calcestruzzo, rispettivamente fy e fck. Si imposta una base di 30 cm e si ricava quindi il predimensionamento della sezione di altezza 45 cm (considerando lo spessore del copriferro di 5 cm).

Si ottengono di conseguenza gli altri valori necessari per la verifica all’abbassamento, quali il modulo E, il momento di inerzia della sezione rettangolare e il peso proprio della trave.

Anche in questo caso, come nei precedenti si ottiene un abbassamento ammissibile dalla struttura pensata.

Conclusioni: effettuando altre prove di calcolo sul foglio di calcolo l’aspetto più importante per un aggetto è la luce, nel caso del c.a. essa al massimo può arrivare ad allungarsi di soli 40 cm per poter ancora considerare lo spostamento ammissibile in tali condizioni di carico; 20 cm per il legno e soli 10 cm per l’acciaio!

 

 

 

Dimensionamento a deformabilità trave in acciaio

 

Per la terza esercitazione era richiesto il dimensionamento di una trave a sbalzo, tenendo conto delle caratteristiche dei solai dimensionati nella precedente esercitazione.
Rispetto alla struttura della volta scorsa, però, sono io a stabilire l'entità dell'aggetto, che decido essere di 2 metri. Ciò comporta che la trave più sollecitata - quella centrale - debba coprire un'area di influenza di 2x3 metri.
 

Adottando una IPE 300, come per la trave che sorregge il solaio nel tratto precedente, il rapporto tra luce e abbassamento è di troppo superiore a 250.

Preferisco quindi diminuire le dimensioni della trave, almeno in quest'ultimo tratto, scegliendo invece una IPE240 che, come dimostrato dalla tabella riportata, soddisfa comunque i requisiti imposti

 

Dimensionamento a deformabilità trave in cemento

 

Anche in questo caso riutilizzo la struttura dell'esercitazione scorsa, mettendo però un aggetto di 2m che determina un'area di influenza per la trave centrale di 2x6 metri

 

Dimensionamento a deformabilità trave in legno

 

 

 

 

Scopo di questa esercitazione è quello di fare una verifica ad abbasamento di uno sbalzo usando le tre tecnologie dell'esercitazione precedente.

Per prima cosa disegno una generica carpenteria del solaio e dello sbalzo.

Secondo passo è di inserire i carichi precedentemente analizzati nel foglio excell per la verifica ad abbassamento.

Rispetto al precedente foglio excell, il calcolo del momento invece di ql³/8 usato per la trave doppiamente appoggiata, è di ql³/2

Nei tre casi il rapporto tra la luce dello sbalzo e il suo abbassamento deve essere maggiore o uguale a 250. 

_Sbalzo in acciaio:

Il profilato necessario per soddifare l'inerzia della sezione è una IPE 330. Utilizzando questo profilato si arriva appena al valore di 250. Per superare questo valore usiamo la IPE 360

_Sbalzo in legno:

Inserendo i carichi e partendo da una base minina di 25 cm, si fanno due prove, una non rispettando il valore di altezza minima imposto e uno rispettanto e ingegnerizzando l'altezza della trave

_Sbalzo in cemento armato:

Inserendo i carichi e partendo da una base minina di 20 cm, si fanno due prove, una non rispettando il valore di altezza minima imposto e uno rispettanto e ingegnerizzando l'altezza della trave