DIMENSIONAMENTO DI UNA TRAVE A SBALZO
Facendo riferimento alla prima esercitazione, ipotizzo 3 differenti tecnologie per il solaio: solaio in c.a., solaio in acciaio e calcestruzzo e solaio in legno
3) SOLAIO IN LEGNO
-trave principale
-travetti in legno lamellare , base 12 cm peso 7 kn/m2
-assito di legno 3,5 cm, peso
-isolante termico in fibra di legno 6 cm, peso 50 kg/m2
-pavimentazione in piastrelle di gres 2 cm, peso 44,5 kg/m2
FASE PROGETTUALE
A) interasse travetto=4m
B) qs -carichi strutturali= 0,23 kn/m2
C) qp -carichi permanenti=2,87 KN/m2
D)qa-carichi accidentali =2 KN/m2
E)qu - somma del carico lineare sulla trave =30,416 kn/m
F)Luce =2m
G)M - momento massimo della trave =60,832 KNm
Nella prima esercitazione viene scelta la resistenza caratteristica del legno GL24h. La normativa prevede inoltre diverse classi di servizio che tengono conto della
temperatura, dell’umidità dell’ambienta in cui si trova il legno. Viene scelta la classe 1. Consultando le tabelle si ricava:
H)fmK- resistenza caratteristica legno=24 N/mm2
I)kmod- =0,8
J)Ym=1,45
Con questi valori il foglio excel calcola la tansione di progetto fdc
K)fdc = 13,24
Si ipotizzi la base della sezione della trave:
L) b = 20 cm
M) Hmin=37,12 cm
Si ingegnerizzi la Hmin in un H maggiore
N) H= 40 cm
Possiamo trascurare il peso proprio della trave in legno in quanto leggera.
Si consideri quindi la trave con sezione 20x40 cm.
FASE DI VERIFICA ALLO STATO LIMITE DI ESERCIZIO
O)si imposti il modulo elastico E = 8000 N/mm2
Il foglio excel calcola :
P) Ix=106667 cm4
Q)qe= (qs+ qp+ qa* 0,5)i = 16KN/m (carico totale)
R) Vmax = 0,38 cm ( abbassamento massimo)
S)l/ Vmax = 520,33 (rapporto tra luce e abbassamento)
VERIFICA
T) SI, la sezione è verificata perché l/ Vmax = 520,33≥ 250.
3) SOLAIO IN ACCIAIO
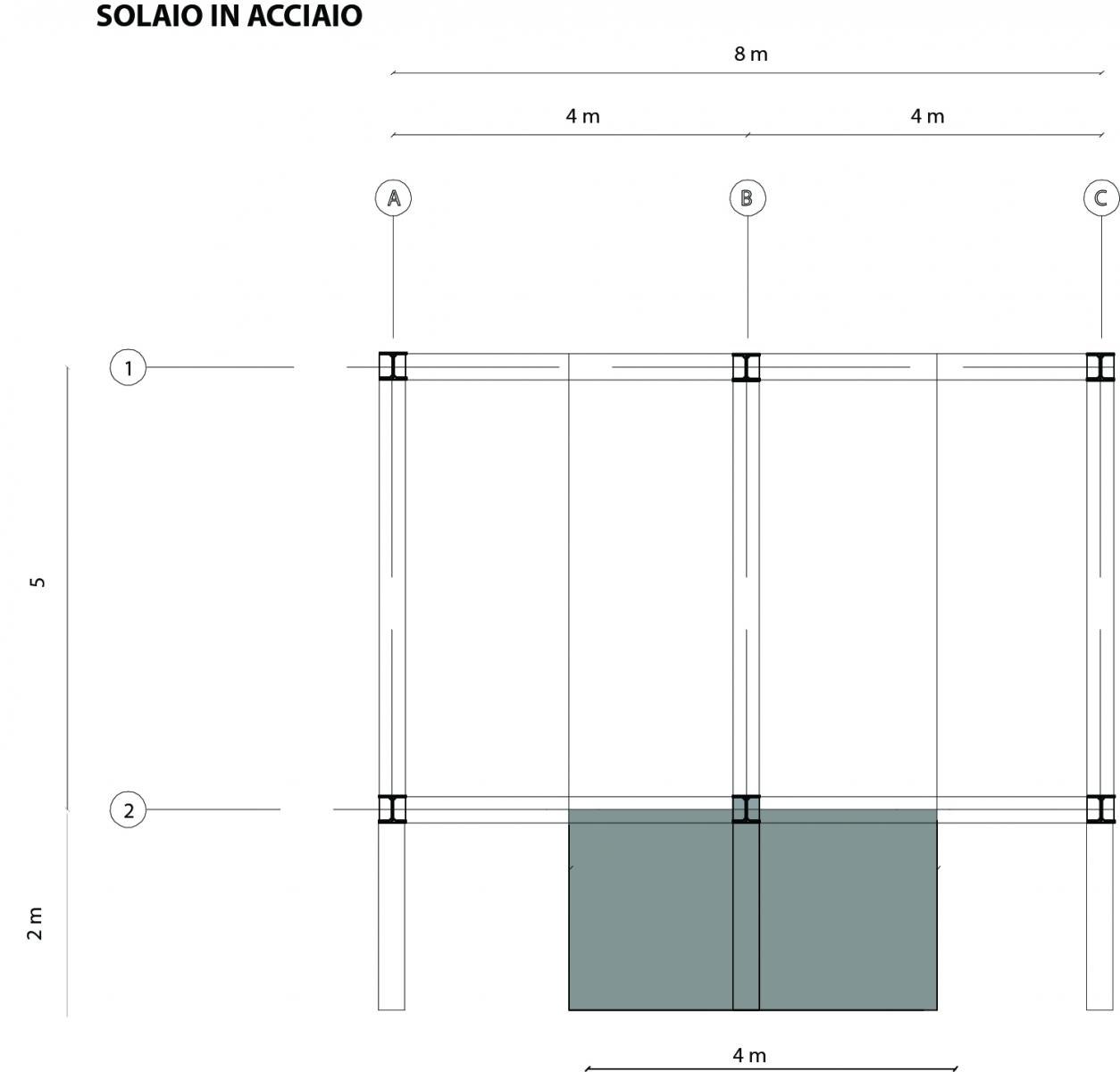
in una seconda ipotesi, il solaio è in acciaio e calcestruzzo,così composto:
-trave acciaio
-trave secondaria IPE 12, peso 10,4 kg/m
-lamiera grecata e getto di calcestruzzo 12 cm, peso 2 kn/m2
-isolante termico in fibra di legno 6 cm, peso 50 kg/m2
-pavimentazione in piastrelle di gres 2 cm, peso 44,5 kg/m2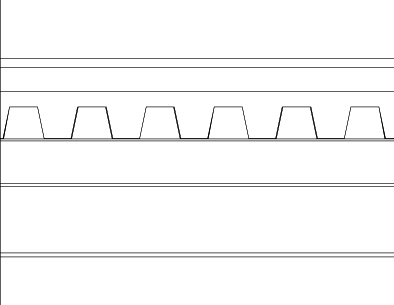
FASE PROGETTUALE
A) interasse travetto=4m
B) qs -carichi strutturali : in questo caso gli elementi strutturali sono la trave IPE 12 e
la soletta collaborante con lammiera grecata: 0,96 KN/m2
C) qp -carichi permanenti: pannello isolante, massetto e pavimentazione =2,48 KN/m2
D) qa-carichi accidentali =2 KN/m2
E)qu - somma del carico lineare sulla trave =31,8 kn/m
F)Luce =2m
G)M - momento massimo della trave =63,744 KNm
H) fYK- tensione di snervamento caratteristica acciaio FE430/S275=275 N/mm2
Il foglio excel calcola:
I)la tensione di progetto fd= 261,90 n/mm2
J)Wxmin- modulo di resistenza =243,39 cm3
Si consultino le tabelle e si ingegnerizzi trovando un profilo IPE con un W>di Wxmin
Si consideri quindi il profilo IPE220.
FASE DI VERIFICA ALLO STATO LIMITE DI ESERCIZIO
in base al profilo scelto si ricavano dalla tabella:
K) il momento d’ inerzia Ix= 2770 cm4
L)il peso = 26,2 kg/m , ovvero 0,262 kn/m
M)il foglio excel calcola il carico totale incluso il peso proprio della trave che al contrario del legno viene considerato qe= 18,022 kn/m
N) si inserisca il modulo elastico E= 210.000n/mm2
O) Vmax = 0,620 cm ( abbassamento massimo)
S)l/ Vmax = 322,8 (rapporto tra luce e abbassamento)
VERIFICA
Q) SI, il profilo IPE220 è verificato, perché l/ Vmax = 322,8 ≥ 250.
3) SOLAIO IN C.A.
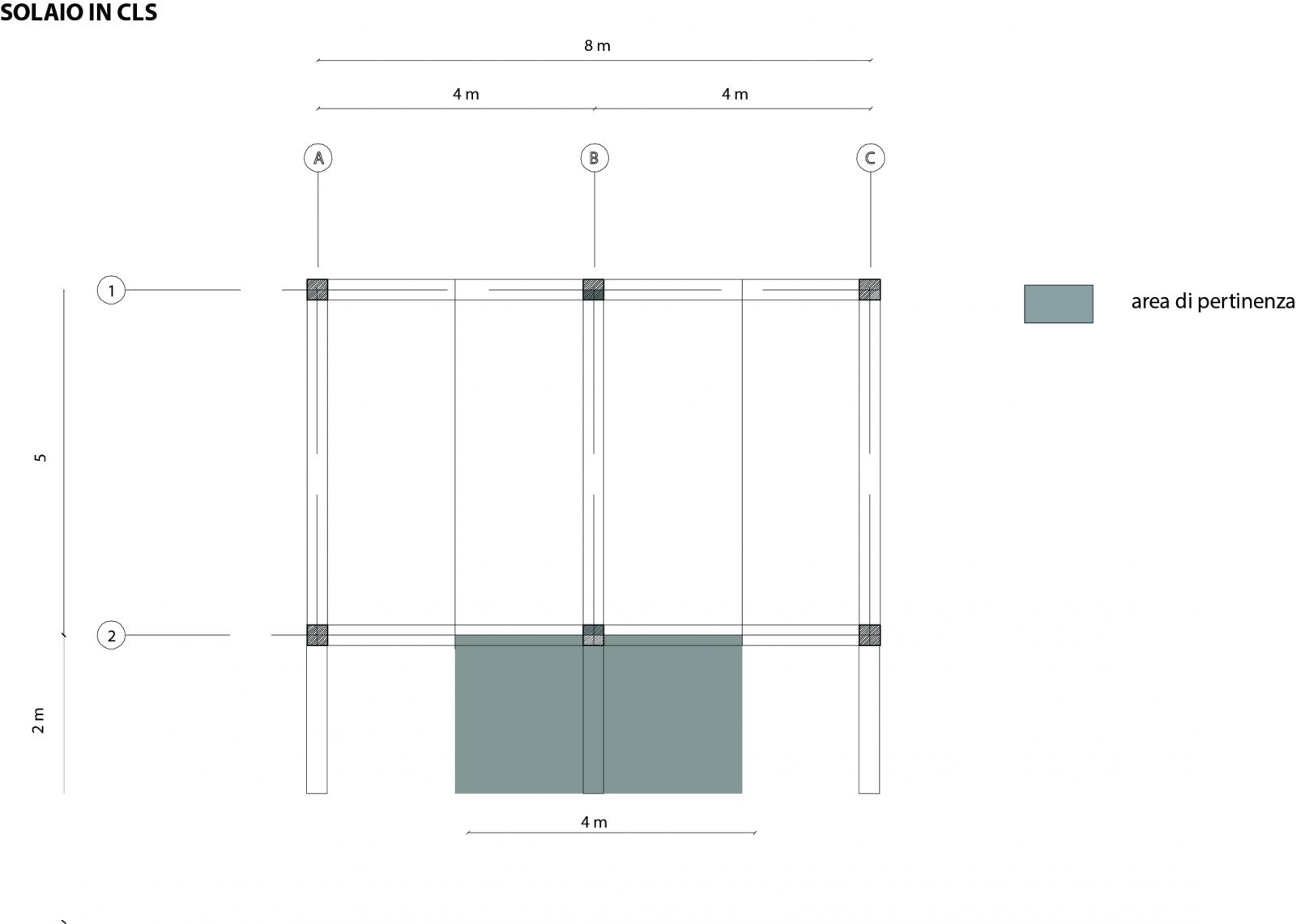
In questa prima ipotesi, il solaio è così composto:
-intonaco interno 1 cm, peso 18 kn/m3
-elementi in laterizio (pignatte) 40x20x25, peso 9 kg cad.
-soletta collaborante in calcestruzzo 4 cm, peso1900 kg/m3
-isolante termico in fibra di legno 6 cm 50 kg/m3
-massetto in calcestruzzo 4 cm, peso1900 kg/m3
-malta di allettamento 2 cm, peso1520 kg/m3
-pavimentazione in piastrelle di gres 2 cm, peso 44,5 kg/m2
FASE PROGETTUALE
A) interasse travetto=4m
B) qs - carichi strutturali : vengono calcolate e poi inserite nel foglio di calcolo gli elementi strutturali che incidono in 1 m2, dunque travetti, soletta collaborante e pignatte= 0,96 KN/m2
C) qp -carichi permanenti: calcolo del peso degli elementi non strutturali del solaio, ovvero intonaco, pannello isolante, massetto, malta di allettamento e pavimentazione.
Il peso va poi incremento con due coeffincienti, che tengono conto del peso dei tramezzi (1 KN/m2)edegli impianti (0,5 KN/m2), definiti dalla normativa =2,48 KN/m2
D) qa-carichi accidentali =2 KN/m2
E)qu - somma del carico lineare sulla trave =31,87 kn/m
F)Luce =2m
G) G)M - momento massimo della trave =63,74 KNm
Si scelgano le resistenze caratteristiche dell’ acciaio e del cls :
H) )fyk= tensione caratteristica di snervamento dell'acciaio da armatura(la normativa prevede un valore superiore a i 450N/mm2)=450 N/mm2
L) resistenza caratteristica a compressione del cls fck= 80 N/mm2
Ora il foglio excel ricaverà:
I) fyd tensione di progetto dell'acciaio=391,30 N/mm2
k) fcd tensione di progetto del cls = 45,33 N/mm2
L) β =0, 63
M)r=2,00
N) si ipotizzi una base = 18 cm
O) il foglio excel ricava ora l’ Hu= 17,67 cm
P) δ copriferro, ovvero il calcestruzzo che protegge l’armatura interna =5 cm
Q) Hmin=22,67 cmaltezza totale della trave che viene quindi ingegnerizzata in:
R) H altezza totale della trave: viene quindi ingegnerizzata l’altezza della trave, che risulta essere verificata 25,00cm
Si consideri quindi la sezione 18x25 cm.
FASE DI VERIFICA ALLO STATO LIMITE DI ESERCIZIO
in base alla sezione scelta si ricavano dalla tabella:
S) Area= 0,05 m2
T)il peso = 1,13kn/m
U) carico totale incluso il peso proprio della trave che al contrario del legno ,viene considerato
qe= 18,89 kn/m
V) si inserisca il modulo elastico E= 210.000n/mm2
W) Ix momento di inerzia=23438 cm4
X)Vmax = 0,77 cm ( abbassamento massimo)
Y)l/ Vmax = 260,62 (rapporto tra luce e abbassamento)
VERIFICA
Z) SI, la sezione 18x25 cm è verificata, perché l/ Vmax = 260,62 ≥ 250.
Fig.1
Fig. 2
Fig. 3
Seleziono poi DEFINE-LOAD PATTERN e compilo un nuovo pattern con il nome asta e self weight multipler: 0, poi digito ADD NEW LOAD PATTERN.
Abbiamo così inserito il carico che andrà a gravare sulla nostra trave reticolare.
Apro nuovamente il comando DISPLAY , seleziono SHOW FORCES/STRESSES e FRAMES/CABLES/TENDONS.
Apriamo nuovamente il comando DISPLAY-SHOW TABLES
f.1
f.2
f.4
f.6 (la prima riga rappresenta la mia trave)
