SdC(b) (LM PA)

Nei progetti architettonici spesso si ricorre all'utilizzo di aggetti per avere degli effetti compositivi particolari

La struttura che sostiene gli sbalzi è la "Mensola".

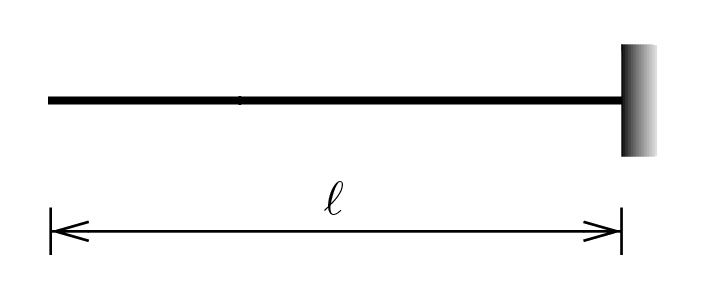
La mensola è una struttura isostatica ( dove le possibilità di movimento di traslazione e rotazione sono bloccate dallo stesso numero di gradi di vincolo ) che rappresenta l'incastro di una trave in una parete o un aggancio a una struttura portante.

Prendendo come riferimento la stessa struttura utilizza nalla prima esercitazione, ho aggiunto un aggetto alle travi principali.

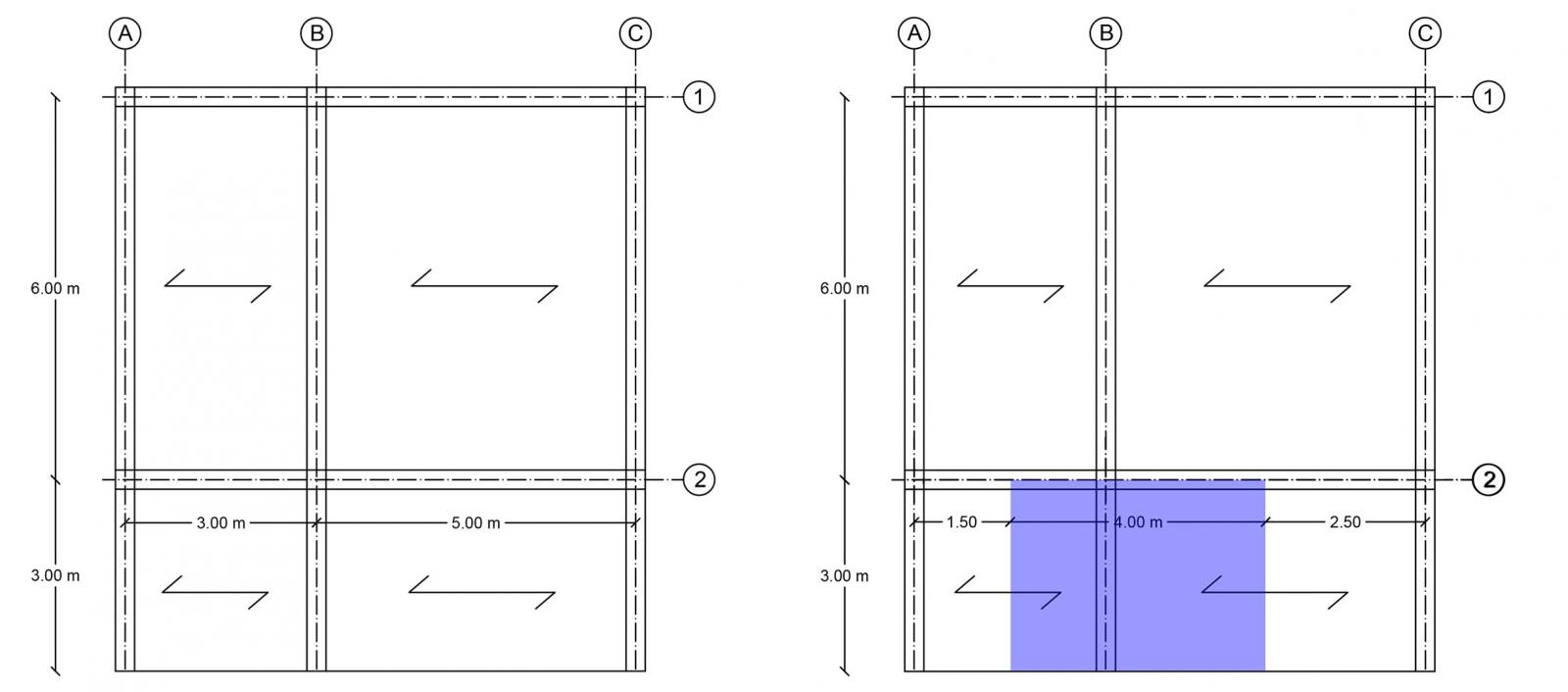
La struttura proposta è un telaio e in realtà la configurazione strutturale delle travi principali è quella di travi appoggiate appogiate e non di strutture incastrate

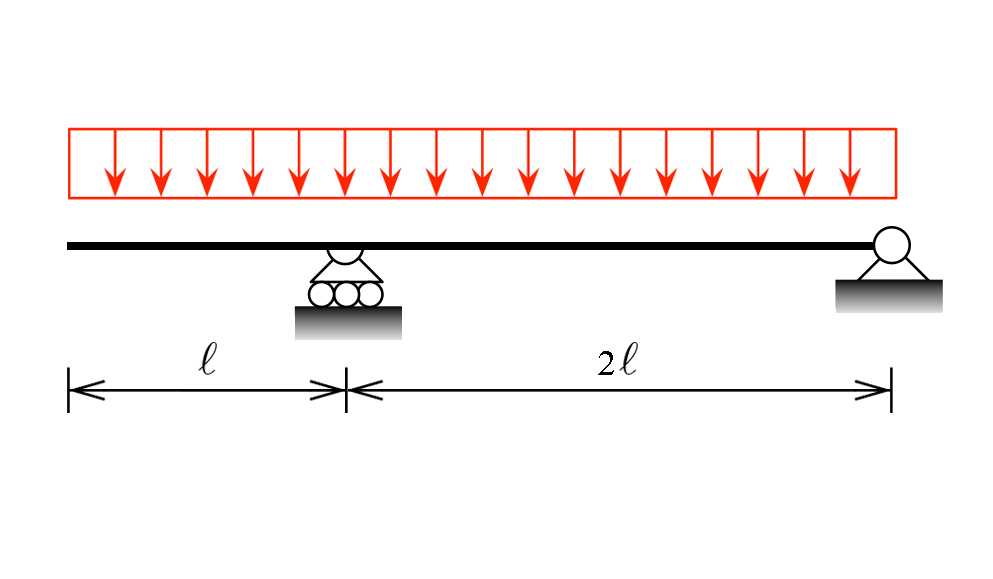
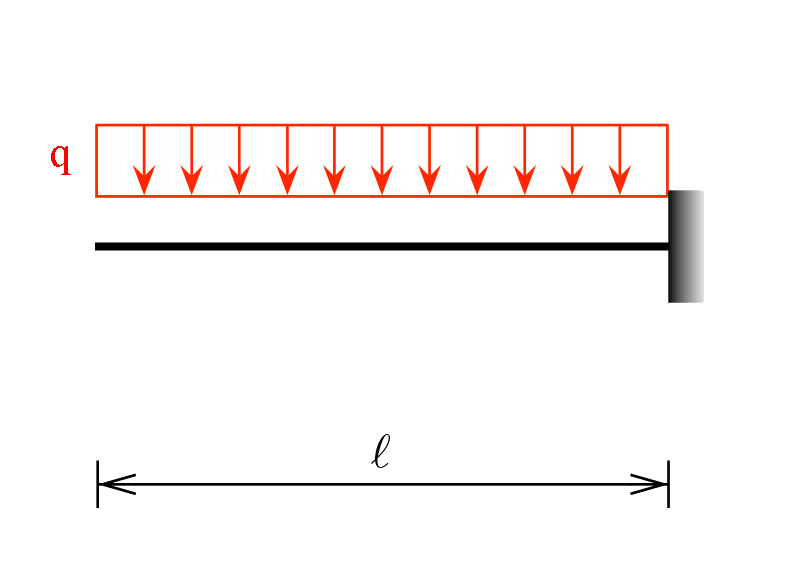
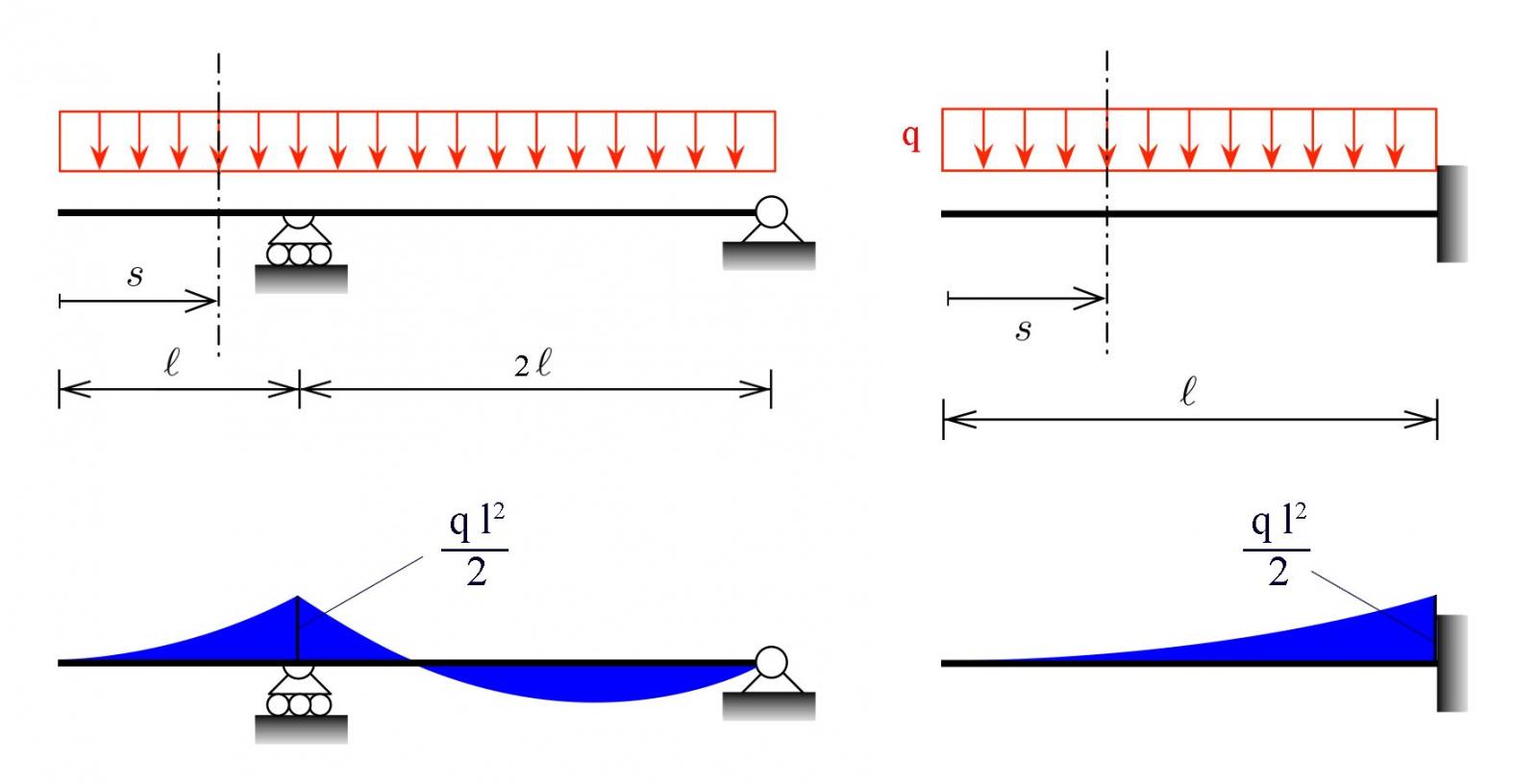
Nel nostro caso però possiamo comunque utilizzare una struttura doppiamente appoggiata perchè guardando le leggi del Momento risultano uguali per entrambi i modelli

M(s) = (q s^2) /2 con valore massimo di Mmax = (q l^2)/ 2 quando s = l

DIMENSIONAMENTO DELLE MENSOLE

I valori dei carichi e le sezioni dei solai sono stati prese dall'esercitazione 1 (vedi http://design.rootiers.it/strutture/node/1740)

Mensola in C.A

Analisi dei carichi:

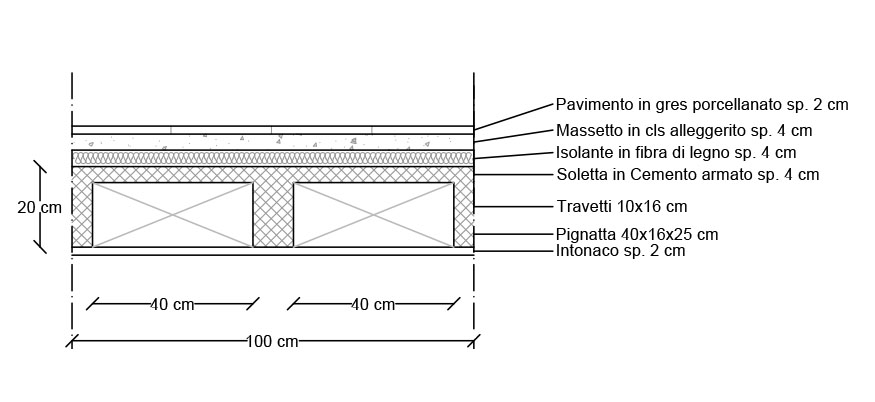
Qs = 0,8 kN/mq + 1 kN/mq + *0,64 kN/mq  = 2,44 kN/mq
Qp = 1 kN/mq + 0,056 kN/mq + 0,72 kN/mq + 0,4 kN/mq + *1 Kn/mq + *0,5 kN/mq =  3,076 KN/mq =  3,08 kN/mq
Qa = 2 kN/mq   valore dipendente dalla Tabella 3.1.II delle NTC 2008 per un ambiente ad uso residenziale

*i valori asteriscati (muri interni e impianti) sono consederati con dei valori forfettari perchè ci possono essere delle modifiche durante in tutta la vita utile dell'edificio

A differenza della precedente esercitazione, la luce della trave è di 3 metri

il carico ultimo risulta quindi essere:
Qu = 2,44 kN/mq x 1,3 + 3,08 kN/mq x 1,5 + 2 kN/mq x 1,5   = 27,12 kN/mq x 4 metri di interasse 
= 43,14 kn/mq

fissando la base della sezione in CA a 30 cm ottengo una altezza minima ingegnerizzata di 55 centimetri (verificata anche con il peso della trave)

La trave risulta dimensionata, ma da Norma NTC 2008 va verificato che l'abbassamento sia inferiore di un 250 della luce Vmax/Luce < 250  (oppure per formula inversa Luce/Vmax > 250)
Per la trave di CA risulta un rapporto luce/abbassamento di 857,38

Qe è il valore di carico allo SLE (Stato Limite d'Esercizio )
E è il Modulo Elastico
Ix è il Momento di Inezia
Vmax è l'abbassamento massimo ammissibile

Il valore dell'abbassamento è determinato dall'equzione della linea elastica.

La linea elastica si basa sul modello di trave di Eulero - Bernoulli.

Nel caso della mensola con carico distribuito, non ci sono forze orizzanti p [s] ne carichi di momento μ [s], dunque non ho sforzi normali, Il taglio deve equilibrare la risultate del carico verticale e in più il taglio risulta la derivata del momento.

Il modello di trave può essere riscritto così:

Dalle condizioni di compatibilità risulta che:
la rotazione *ϑ [s]   è la variazione di spostamento v rispetto ad s (v ' [s] derivata di v rispetto alla generica sezione s)
la curvatura χ [s] è la variazione della rotazione respetto ad s

Dai Legami costitutivi risutal che M [s] = E J χ [s] (per la Formula di Navier)
dove E è il Modulo Elastico del materiale
J è il momento di inerzia
χ [s] è la curvatura 

*(la rotazione può essere scritta come ϕ)

Mettendo insieme tutte le relazioni dalla legge del momento è possibile ricavare curvatura, rotazione e abbassamento della trave a secondo della posizione di una generica sezione S lungo la trave.

ϑ [s] = v ' [s] per ottenere v devo fare l'integrale rispetto ad s quindi:

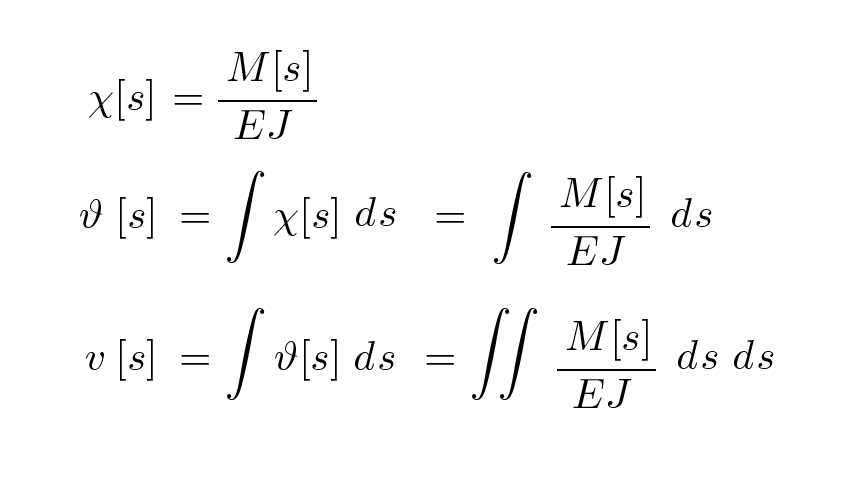
In Base alla legge del momento ottengo una legge almeno del secondo grado dato che per ottenere una funzione che sia derivabile due volte.
Se v [s] è una funzione del secondo grado, M [s] è una legge costante. Dunque il Taglio è nullo e non c'è carcico verticale
Se v [s] è una funzione del terzo grado, M [s] è una legge lineare. Dunque il Taglio è un valore costante e il carico è una forza verticale puntuale

Se v [s] è una funzione del quarto grado, M [s] è una legge parabolica. Dunque il Taglio è un valore lineare e il carico verticale è distribuito su tutta la trave.

Se v [s] è una funziona del quinto grado, M [s] è una legge cubica. il Taglio è parabolico e il carico verticale è lineare. (un carico del genere può essere il carico della neve sui tetti)

e così via.

Nel caso della mensola

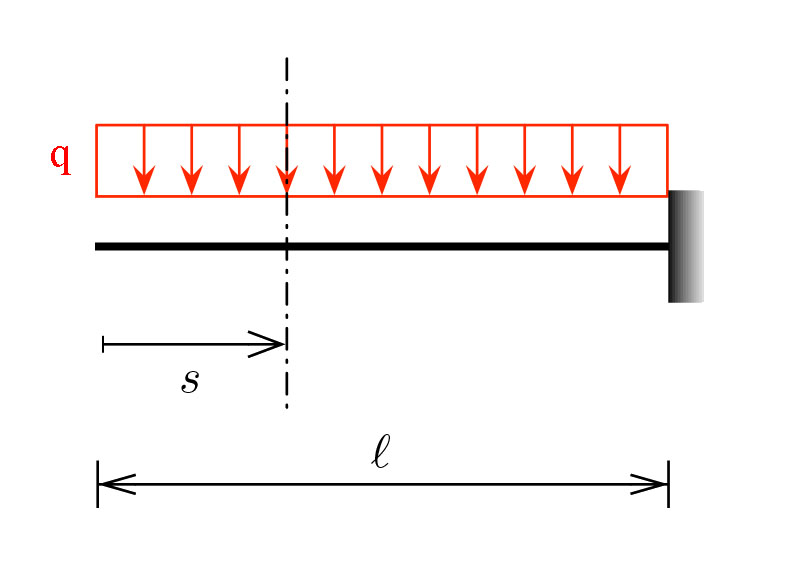
la legge del momento risulta:

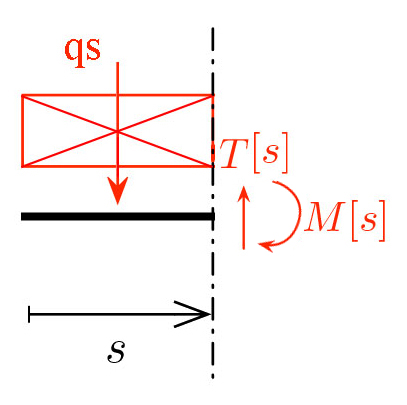
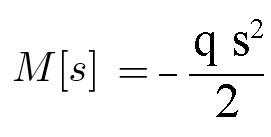
C1 e C2 sono costanti che escono fuori dall'integrale indefinito. Per poter determinare i valori delle costanti ho bisogno di punti in cui conosco sicuramente i valori di spostamento e/o rotazione.

In questo caso con la mensola la deformata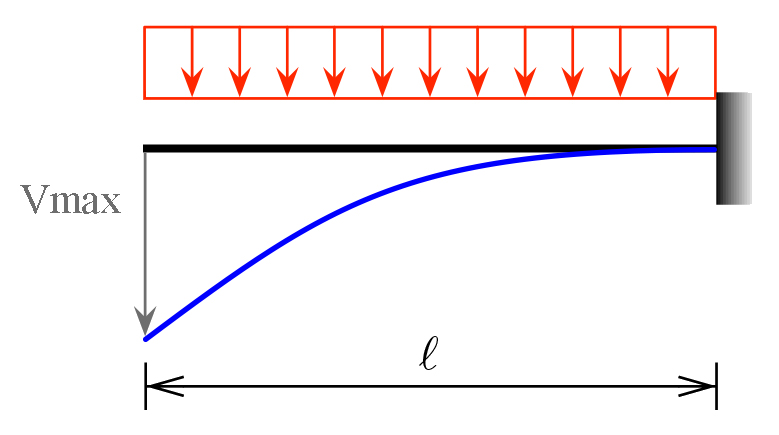 

Nella mensola conosciamo questi valori all'incastro dove lo spostamento e la rotazione sono nulli

Dopo aver determinato C1 e C2 l'equazione della linea elastica risulta

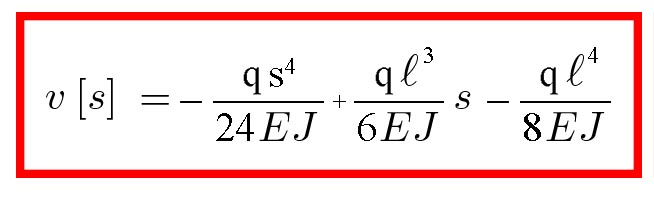
Dato che l'abbassamento massimo risulta essere all'inizio della trave.
Calcolo l'abbassamento in s = 0 quindi Vmax = V0

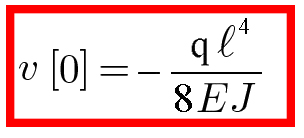
Mensola in Acciaio

Analisi dei carichi

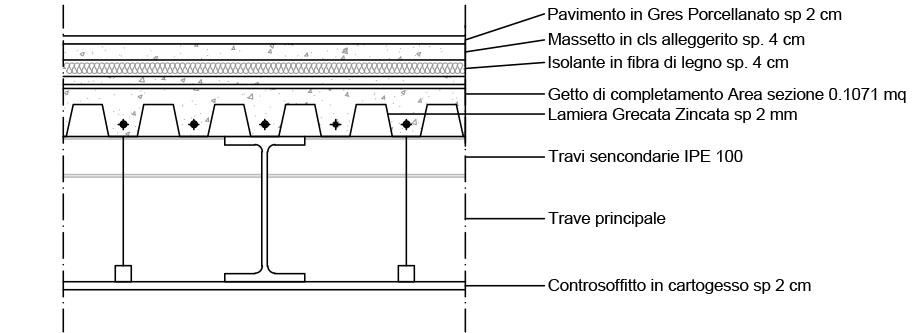
Qs = 1 kN/mq + 0,157 kN/mq + 0,081 kN/mq  = 1,238 kN = 1,24 kN/mq 
Qp = 0,078 kN/mq + 0,056 kN/mq + 0,72 kN/mq + 0,4 kN/mq + *1 Kn/mq + *0,5 kN/mq =  2,75 KN/mq
Qa = 2 kN/mq valore dipendente dalla Tabella 3.1.II delle NTC per un ambiente ad uso residenziale

Qu = 2,94 kN/mq x 1,3 + 2,75 kN/mq x 1,5 + 2 kN/mq x 1,5  = 44,55 kn/mq

*i valori asteriscati (muri interni e impianti) sono consederati con dei valori forfettari perchè ci possono essere delle modifiche durante in tutta la vita utile dell'edificio

Il profilo necessario per resistere alla flessione è un IPE 360 (verificata anche con l'aggiunta del peso della trave stessa).

Il profilo scelto ha un rapporto tra luce e abbassamento di 370,189 quindi il profilo scelto risulta verificato anche all'abbassamento.

Mensola in Legno

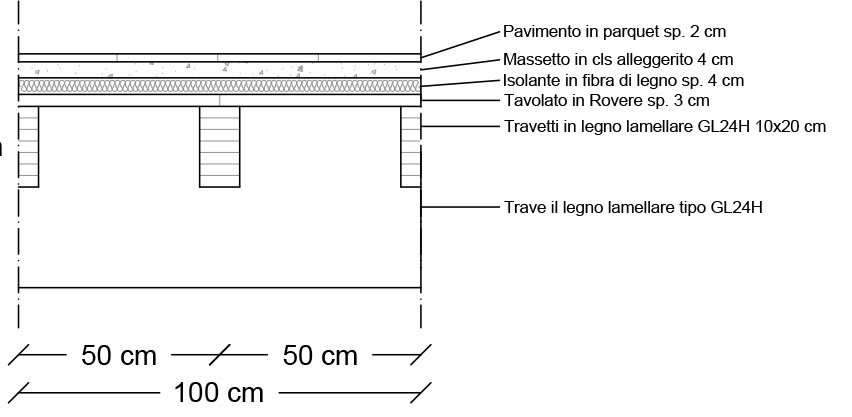
Analisi dei Carichi:

Qs = 0,078 kN/mq + 0,216 kN/mq = 0,292 kN/mq = 0,3 kN/mq  
Qp = 0,056 kN/mq + 0,72 kN/mq + 0,144 kN/mq + *1 Kn/mq  + *0,5 kN/mq  =  2,26 kN/mq
Qa = 2 kN/mq valore dipendente dalla Tabella 3.1.II delle NTC per un ambiente ad uso residenziale

Qu = 0,3 kN/mq x 1,3 + 2,26 kN/mq x 1,5 + 2 kN/mq x 1,5  = 27,12 kN/mq

Nella trave di Legno Lamellare per determinare l'abbassamento non considero il peso della trave principale (perchè è un materiale molto leggero e il peso della trave principale non influesce fortemente sul carico strutturale)

*i valori asteriscati (muri interni e impianti) sono consederati con dei valori forfettari perchè ci possono essere delle modifiche durante in tutta la vita utile dell'edificio

Utilizzo una trave in legno lamellare in classe 2, con classe di durata del carico di lunga durata che implica un coefficiente riduttivo di resistenza Kmod di 0,7 

fissando la base della trave a 25 cm risulta necessaria una trave in legno lamellare ingegnerizzata di 55 cm.

Poichè il rapporto tra abbassamento è di 576,97 la trave è a Norma.

Considerazioni:

La mensola in C.A ha dimensioni 30x55 cm con un rapporto luce/abbassamento di 857,38
La mensola in Acciaio è un IPE 360 (altezza del profilo 36 cm) con un rapporto luce/abbassamento di 370,189
La mensola in Legno ha dimensioni 25x55 cm con un rapporto luce/abbassamento di 576,97

tra le tre travi, quella che ha un abbassamento minore è quella in CA, e quella con un abbassamento maggiore è quella in acciaio. L'acciaio permette di coprire luci con un altezza della trave più piccola rispetto agli altri materiali, ma a causa del suo comportamento duttile ha un abbassamento molto maggiore. Cemento è un materiale molto più pesante rispetto agli altri ma ha un comportamento molto rigido, infatti il suo abbassamento è meno della metà di quello dell'acciaio.
Il legno è una situazione intermedia tra gli altri due materiali. Ha dimensioni minori del cemento armato, ha un abbassamento di poco superiore al cemento, maggiore dell'acciaio ed molto più leggero rispetto agli altri due materiali.

Se avessi bisgono di strutture leggere conviene utilizzare il legno.
Per strutture snelle che sostengono tanto carico conviene l'acciaio.
Se avessi bisogno invece di strutture che si devono abbassare di meno conviene utilizzare il CA

Prendendo in considerazione i dati calcolati nella precedente esercitazione (carichi del solai) , vado a ricavarmi l'altezza minima della trave per quanto riguarda il cemento armato ed il legno e la resistenza a flessione minima per l'acciaio. Dovendo progettare una trave a sbalzo l'unica differenza di calcolo che si può riscontrare rispetto alla precedente esercitazione è  nella formula del momento massimo , non più ql^2/8 ma  ql^2/2 poichè il sistema equivale a quello di una mensola. Dopo aver progettato la sezione della mia trave in tutte le tecnologie, per questo sistema statico si considera  un altro fattore: LA DEFORMABILITA'. La verifica a deformabilità  si basa sul rapporto della luce della mia trave (sbalzo) e l'abbassamento massimo, che deve essere >250. Essa non viene effettuata allo SLU (stato limite ultimo -collasso), ma allo SLE (stato limite di esercizio-funzionalità ed efficienza).

Inizio la mia esercitazione con la carpenteria che sarà uguale per tutte le mie strutture. La trave evidenziata in rosso è la trave più sollecitata. La luce sarà di 3m e l'interasse di 5m. Per cui la mia area d'influenza sarà di 3mx5m = 15mq  

CEMENTO ARMATO :

qs = 2,46 KN/mq                      qp =  3,1 KN/mq                  qa = 2 KN/mq

Si andrà a calcolare il carico ultimo (qu) sommando tutti i carichi (strutturali, permanenti e accidentali) moltiplicati per i propri coefficienti di sicurezza ed infine moltiplicati per l'interasse.

                               qu =   (  qs x 1,3 + qp x 1,5 + qa x 1,5 ) x 5 =  54,34 KN/m

Momento max = 244,08 KNm

Ipotizzo la base della mia trave pari a 40 cm e risulta un altezza minima di 50,77cm che andrò ad ingegnerizzare portandola ad un altezza ultima di 55cm. La sezione della trave sarà di 40cmx55cm ed è VERIFICATA  considerando naturalmente anche il peso proprio della trave progettata con un Fyk = 450Mpa e Fck di 30Mpa.

Deformabilità:

 Il peso proprio della trave utilizzato precedentemente per la progettazione della sezione allo SLU, adesso viene riutilizzato per trovare il qe= carico totale allo SLE. Il carico totale qe=38,30KN/mq, il modulo elastico E=210000Mpa ed il momento d'inerzia Ix=55453 cm^4 mi permettono di trovare l'abbassamento massimo vmax=0,33cm Se il rapporto tra la L(luce)/vmax > 250 allora l' abbassamento massimo della mia trave a sbalzo è verificato. Nella mia esercitazione ottengo un L/vmax = 900,98 > 250 VERIFICATO.

LEGNO:

qs = 0,36 KN/mq                      qp =  3,34 KN/mq                  qa = 2 KN/mq

Si andrà a calcolare il carico ultimo (qu) sommando tutti i carichi (strutturali, permanenti e accidentali) moltiplicati per i propri coefficienti di sicurezza ed infine moltiplicati per l'interasse.

                                qu =   (  qs x 1,3 + qp x 1,5 + qa x 1,5 ) x 5   =  42,39KN/mq

Momento max = 190,775 KNm

Ipotizzo la base della mia trave pari a 35 cm e risulta un altezza minima di 58,60cm che andrò ad ingegnerizzare portandola ad un altezza ultima di 60cm. La sezione della trave sarà di 35cmx60cm

Deformabilità:

Nella fase di progetto della sezione per quanto riguarda il legno, essendo un materiale leggero,il peso proprio della trave progettata viene trascurato, quindi, nella formula per trovarci qe( il carico totale allo SLE) ,non viene sommato. Il carico totale allo SLE qe=24KN/mq, il modulo elastico E=8000Mpa e il valore del momento d'inerzia Ix=630000cm^4 (b*h^3/8) mi permettono di trovare l'abbassamento massimo vmax=0,47cm .Se il rapporto tra la L(luce)/vmax > 250 allora l' abbassamento massimo della mia trave a sbalzo è verificato. Nella mia esercitazione ottengo un L/vmax = 635,46 > 250 VERIFICATO

ACCIAIO:

qs = 2,12 KN/mq                      qp =  2,98 KN/mq                  qa = 2 KN/mq

                                     qu =   (  qs x 1,3 + qp x 1,5 + qa x 1,5 ) x 5   = 51,13 KN/mq

Momento max = 230,085 KNm

Scegliendo l'acciaio Fe 430/S275 che avrà una tensione di snervamento pari a 275Mpa otterrò un modulo di resistenza Wxmin pari a 878,51 cmc che equivale ad un IPE 360 perchè considero un Wx pari a 904cmc.

Deformabilità:

Prendendo quindi in considerazione un IPE 360 avrò il peso della trave pari a 0,571 KN/m (che verrà sommato ai carichi del solaio ), un momento d'inerzia Ix=16270 cm^4 ed un modulo elastico E=210000Mpa. Tutti questi dati mi permettono di trovare l'abbassamento massimo della mia trave a sbalzo pari a  vmax=0,921cm. Se il rapporto tra la L(luce)/vmax > 250 allora l' abbassamento massimo della mia trave a sbalzo è verificato. Nella mia esercitazione ottengo un L/vmax = 325,820 > 250 VERIFICATO.

La seconda esercitazione consiste nel dimensionamento di una travatura reticolare 3D attraverso il software SAP. Per prima cosa impostiamo le unità di misura (KN, m, C) e un nuovo modello grid only. Dopo inserisco i valori x, y, z e vado a creare la griglia su cui disegno la mia trave reticolare. Attraverso il comando Drow Freame disegno le aste, completato il primo modulo, le copio prima sull'asse delle x e poi su quello delle y con il comando ctrlv - ctrlc.

Una volta disegnata la trave reticolare verifico che i nodi coincidono con il comando Marge joins che mi corregge le imperfezioni.

A questo punto procedo con l'analisi e inserisco i vincoli nei quattro angoli della struttura, essendo una trave reticolare i vincoli che andrò a inserire sono tutte cerniere. 

Nel caso della struttura reticolare nei nodi devo avere delle cerniere, non un incastro come di solito avviene. Quindi seleziono la struttura, assaine, frame, releses a questo punto mi si aprirà una finestra e seleziono Moment 22 e Moment 33 seleziono ok e avrò le cerniere in tutti i nodi. In questo modo si impone che ogni asta sia collegata all'altra mediante un vincolo di cerniera interna, quindi non trasmetterà momento.

Ora vado a creare il carico ripartito, quindi vado su Define, Section Properties, Frame section, Add new e vado a crearmi la sezione e il materiale delle aste. I profilati scelti per la travatura sono tubolari cavi d'acciaio.

Non prendendo in considerazione il peso proprio della trave, vado su Assine, Joint Loads, Forses Pratters Name e assegno una forza dal valore -100 ai noi selezionati (quelli superiori) in modo che avrò le mie forze concentrate rivolte verso il basso. 

Parte l'analisi del modello, si analizza la stuttura prendendo in considerazione le forze che mi sono creata precedentemente.

La mia stuttura si è deformata. Quindi verifico che ci siano solo sforzi normali.

Estraggo poi le tabelle con i valori di trazione e comressione riferite ad ogni asta su excel per procedere con il dimensionamento.

Sulla tabella Excel pulisco il file dai dati superflui e ordino secodo l'ordine delle aste dal segno negativo a quello positivo. Quindi, ordino la colonna Station facendo sì che i valori siano crescenti, evidenzio in rosso le aste diagonali di 2,83cm e ordino la colonna P in ordine decrescente.

Apro il file fornitoci per l'esercitazione. Sarà diviso in due parti resistenza a trazione e resistenza a compressione. Importo i valori ricavati sotto la colonna N, imposto la classe di resistenza del mio materiale (fyd), il valore di E e la luce delle mie aste.In base all'area minima scelgo il tipo di tubolare da utilizzare.L'ultimo passo è quello di verificare che che il profilo sceloto soddisfi le caratteristiche di sollecitazione provocate dalla trazione e dalla compressione.

Iniziamo col definire il modello della struttura reticolare spaziale in SAP2000:

1. Apriamo il software e andiamo su File → New model
2. Impostiamo le unità di misura del modello e scegliamo il template più comodo che in questo caso risulta essere la griglia spaziale triortogonale
3. Della griglia andremo a definire il numero di linee rette nelle direzioni triortogonali x, y, z e la loro spaziatura nei piani triortogonali xy, yz, zx. Con la griglia definita andremo a realizzare il modello di una struttura reticolare spaziale avente tante aste quanto i segmenti definiti dalle linee di griglia più un numero di aste necessarie a 'triangolare' tutta la struttura (al fine di sfruttare la rigidezza del telaio triangolare)
4. Andiamo quindi a disegnare come ci è più comodo non tutte ma un certo numero di aste che poi andremo a copiare e incollare in una delle due direzioni di base
5.  Poi, sempre copiando e incollando nell'altra direzione di base andremo a definire tutte le aste componenti la struttura
6.  Verifichiamo di non aver erroneamente sovrapposto più aste attraverso il comando Edit → Show Duplicates 
7.  Un altro accorgimento è quello di fondere i nodi entro una certa distanza di tolleranza (cioè nel caso in cui non tutte le aste che dovrebbero convergere in un nodo convergono in quel nodo ma convergono in un altro nodo ad una distanza molto piccola dal primo, distanza sicuramente inferiore alla tolleranza che andremo ad impostare). Selezioniamo dunque tutta la struttura e andiamo su Edit → Edit Points → Merge Joints ed impostiamo la Merge Tolerance
8. Imponiamo i vincoli: scegliamo i nodi attraverso i quali la struttura sarà vincolata (io ne ho scelti 3 disallineati, ossia il numero minimo affinche non ci sia labilità), li selezioniamo e andiamo a definirne i gradi di vincolo attraverso il comando Assign → Joint → Restraints... e andando a vietare la traslazione nelle tre direzioni 
9.  Trattandosi del modello di una struttura reticolare, cioè una struttura in cui è presente solo sforzo normale, dobbiamo imporre che tutti i suoi nodi siano delle cerniere. Selezioniamo nuovamente tutte le aste e andiamo su Assign → Frame → Releases/Partial fixity... e rilasciamo momento22 e momento33 all'inizio e alla fine delle aste Nel modello le aste appariranno come se distanziate dai nodi
10. Definiamo le caratteristiche materiche e geometriche delle nostre aste. Selezioniamo tutte le aste del modello e andiamo su Assign → Frame → Frame Sections... e poi su Add New Property......e andiamo a definire materiale, profilo e caratteristiche del profilo (in questo caso ho scelto un tubo circolare di diametro esterno 200mm e di spessore 10mm)
11. Definiamo i carichi agenti sulla struttura da Define → Load Patterns... aggiungiamo un nuovo modello di carico (Add New Load Pattern) lo nominiamo ed impostiamo il peso proprio pari a zero (colonna Self Weight Multiplier)
12. Assegnamo i carichi ai nodi che desideriamo (esclusivamente ai nodi dal momento che parliamo di una struttura reticolare) semplicemente selezionandoli e andando su Assign → Joint Loads → Forces... selezioniamo il tipo di carico da noi poc'anzi definito e definiamo il valore della forza (in questo caso una forza di -10kN lungo l'asse z avendo immaginato la struttura come una copertura)

Siamo finalmente pronti per lanciare l'analisi semplicemente cliccando sul simbolo play (►) e scegliendo di far partire il calcolo esclusivamente per il tipo di carico da noi creato (nel caso specifico Forza Es.2) e cliccando finalmente su Run Now

Terminata l'analisi, tra le varie proprietà che possiamo mettere in evidenza c'è la graficizzazione degli sforzi normali; clicchiamo sul pulsante Show Forces/Stresses quindi su Frames/Cables/Tendons... selezioniamo Axial Force. Possiamo inoltre impostare un fattore di scala o decidere se i diagrammi debbano essere campiti pieni o debbano mostrare anche il valore in cifre

E questo è il grafico ottenuto; in blu è indicato lo sforzo di trazione (N+) ed in rosso lo sforzo di compressione (N-)

Per avere una lettura organica e chiara a questo punto è comodo costruirsi ed esportare una tabella nel quale viene indicato per ogni asta il valore dello sforzo normale (che è costante lungo tutta una qualsiasi asta della struttura). Andiamo su Display → Show Tables... e spuntiamo la casella ANALYSIS RESULTS e diamo quindi l'ok

A questo punto dal menu a tendina selezioniamo Element Forces - Frames

Giocando con le seguenti opzioni ho creato la mia tabella:

• Format: ho deciso quali colonne stampare  e quali no. Ho scelto di stampare le colonne Frame ('Asta'; ciascuna asta è indicata da un numero), Station (punto dell'asta dove è calcolato lo sforzo normale rispetto alle coordinate locali dell'asta) e P (lo sforzo normale espresso in KN)
• Filter: dal momento che, come precedentemente detto, lo sforzo normale è costante lungo tutta l'asta per qualsiasi asta, ho scelto di filtrare la colonna Station solo per i valori = 0 (in questo modo ogni asta compare nella tabella una sola volta)
• Sort: ho deciso di ordinare la tabella per valori decrescenti dello sforzo normale

Siamo ora pronti per esportare la tabella in Excel cliccando dal menù della tabella su File → Export Current Table → To Excel 

Da Excel possiamo rapidamente mettere a confronto i valori massimi di trazione e compressione

Inoltre graficizzando tutti i valori di N appare chiaro che:

• solamente il 2.1% delle aste tese supera il valore di N=150KN
• solamente il 1.3% delle aste compresse supera il valore di N=|150|KN
• il 63.2% delle aste tese subisce una trazione > 50kN
• il 65.9% delle aste compresse subisce una compressione > |50|kN
• il 34.7% delle aste tese subisce una trazione 150kN > N > 50kN
• il 32.8% delle aste compresse subisce una compressione |150|kN > N > |50|kN

Ora possiamo passare al dimensionamento delle aste:

• Aste tese
  Poiché σ = N/A, A = N/σ dove σ equivale in fase di progetto a f_d.
  con:
  • N = rispettivamente Nmax (284.329kN); 150kN; 50kN

  • f_yk = tensione di snervamento caratteristica dell’acciaio scelto espressa in MPa

  • γ_m= coefficiente di sicurezza adimensionale

  • f_d = tensione di progetto il cui valore è dato da f_yk / γ_m

  • A_min = area minima ricavata dal rapporto tra la sollecitazione N e la tensione di progetto f_d

  • A_design = Area ingegnerizzata, cioè l'area del profilo scelto da profilario subito maggiore dell’area minima e quindi a favore di sicurezza.​

• Aste compresse
  Per dimensionare le aste compresse abbiamo bisogno di altri parametri, in quanto dobbiamo tener conto dell'instabilità euleriana. 
  Poiché il carico critico euleriano è:
  f_crit=(π²EA) / λ² 
  allora
  σ_crit=(π²E) / λ²
  e quindi 
  λ_max=π(E/σ_crit)^1/2
  e poiché 
  λ=l₀/rho dove 
  l₀=beta(l)=luce libera d'inflessione con beta=1 per un'asta incernierata alle due estremità
  allora 
  rho_min=l₀/λ_max 
  e poiché 
  rho_min=(I_min/A)^1/2
  allora 
  I_min=A(rho_min)²
  - nella tabella ho assunto σ_crit=f_yd non fidandomi della fase duttile dell'acciaio
  - per l ho preso il valore della luce delle aste più lunghe, cioè quelle diagonali, pari a 2,83m (quelle parallele agli assi del sistema di riferimento hanno invece l=2m)

  Determinati per ciascun carico (determinato come sopra spiegato attraverso la distribuzione delle intensità di sforzo normale) i valori di λ_min, rho_min e I_min, ho trovato nel profilario il profilo che soddisfaceva i tre parametri e li ho inseriti nelle ultime tre colonne rosse verificando che il valore λ risultante dall'ultima colonna fosse <200 (valore massimo della snellezza da normativa per le membrature principali)

La seconda esercitazione consiste nel dimensionamento di una trave reticolare 3D. Creo la struttura reticolare con il programma SAP. Creo un nuovo modello Grid Only con unità di misura KN,m,C. Dopo aver creato la maglia di riferimento Draw Frame mi ricalco la mia trave asta per asta. Creato un primo modulo lo copio su tutta la maglia e controllo che non ci siano doppioni attraverso il comando Edit-Merge Duplicates.

Attraverso il comando Assign-Joint-Restrains vincolo la trave alle quattro etremità con delle cerniere. Dopo aver tolto i momenti dalle aste decido di assegnare alle aste delle sezioni cilindiriche con il comando Assign-Frame-Frame Section.

Una volta tolto il peso proprio della struttura con il comando Define-Load Pattern, selezionando la parte superiore della mia struttura e utilizzando il comando Assign-Joint Loads-Forces assegno una forza di  F:-100KN.

Dopo aver assegnato i carichi faccion partire l'analisi (con il comando Run Analysis), come risultato mi mostrerà la struttura deformata. Verifico inoltre, attarverso il comando Frame/Cable, che ci siano gli sforzi normali, e mi permette di vederli nella struttura senza deformazione. A questo punto per poter dimensionare la trave ho bisogno di esportarmi un foglio excel con tutte le aste e i loro relativi sforzi normali.

La prima cosa che faccio una volta ottenuto il file Excel è eliminare i doppioni e riordino le mie aste soggette a trazione e compressione. Utilizzo due fogli excel diversi: uno per il dimensionamento a trazione e uno per il dimensionamento a compressione. Per quanto riguarda il dimensionameto a trazione: 

Sapendo che A=N/f(yd) e avendo N come valore conosciuto grazie alla mia analisi posso ricavarmi l' area minima che l'asta deve avere. Utilizzando un tabellario individuo l'asta con l'area subito più grande e la inserisco nel mio foglio excel.

Per quanto riguarda il dimensionameto a compressione:

Come ho fatto per la trazione anche qui nello stesso modo mi ricavo l'area minima e aggiungo una nuova casella che mi peremtte di inserire la luce delle mie aste (che nel mio caso sarà 2 e 2,83 per le diagonali). In questo caso due nuovi fattori influenzano la mia trave: il momento di inerzia e il raggio di inerzia. Ingegnerizzando la mia asta devo verificare che i valori I,ro e Lambda del profilato non siano inferiori a I(min), ro(min), Lambda(min).