DIMENSIONAMENTO E VERIFICA DI DEFORMABILITà DI UNA MENSOLA IN LEGNO
Si disegna innanzitutto la pianta di carpenteria di un edificio la cui maglia strutturale si compone di travi e pilastri; si individua la trave maggiormente sollecitata e la sua area di influenza in modo da evidenziarne il suo interasse.
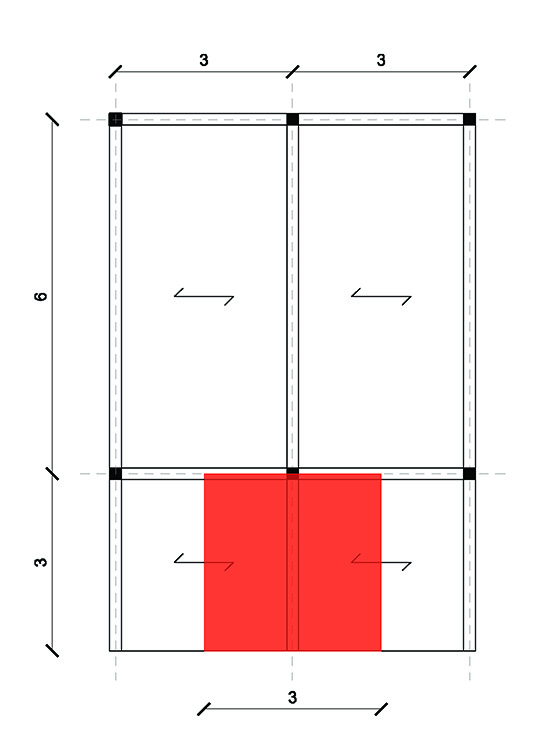
Una volta individuata la pianta di carpenteria si passa alla scelta del solaio tipo che grava sulla trave presa in esame. Ognuno dei materiali che compone la stratigrafia del solaio ha un suo spessore ed un suo peso specifico:
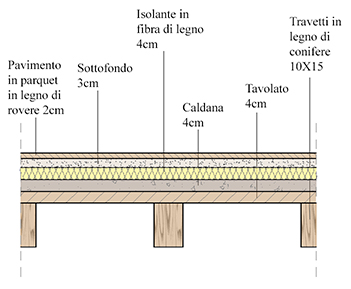
Materiale: Sp. Peso specifico:
-Pavimento in legno di rovere 2cm 820Kg/m3 = 8,2KN/m3
-Sottofondo 3cm 1800Kg/m3 = 18KN/m3
-Isolante in fibra di legno 4cm 200Kg/m3 = 2KN/m3
-Caldana 4cm 7KN/m3
-Assito 4cm 5,3KN/m3
-Travetti in legno di conifere 10X15 6KN/m3
Conoscere lo spessore ed il peso specifico dei materiali che compongono il solaio ci serve per analizzare i carichi che gravano sulla trave che vogliamo dimensionare. Tali carichi si dividono in carichi strutturali qs (KN/m2) nei quali si includono tutti gli elementi che hanno una funzione portante, carichi permanenti qp (KN/m2) nei quali si includono tutti quegli elementi che non hanno funzione portante; carichi accidentali qa (KN/m2) che dipendono dalla funzione che svolge l’edificio.
L’analisi dei carichi del solaio ci serve per determinare il carico di progetto che agisce sulla trave da dimensionare e che si esprime in KN/m.
Quasi tutti i materiali del solaio sono espressi in KN/m3; noi vogliamo sapere quanto volume occupa ogni materiale in un metro quadro di solaio per cui si procede in questo modo:
qs: 0,18 + 0,21 = 0,4 KN/m2
-Travetti in legno di conifere 2 (0,10 x 0,15 x 1) m3/m2 x 6 KN/m2 = 0,18 KN/m2
-Assito (0,04 x 1 x 1) m3/m2 x 5,3 KN/m3 = 0,21 KN/m2
qp: 0,16 + 0,54 + 0,08 + 0,28 + 0,5 + 1 = 2,6 KN/m2
-Pavimento in legno di rovere (0,02 x 1 x 1) m3/m2 x 8,2 KN/m3 = 0,16 KN/m2
-Sottofondo (0,03 x 1 x 1) m3/m2 x 18 KN/m3 = 0,54 KN/m2
-Isolante in fibra di legno (0,04 x 1 x 1) m3/m2 x 2 KN/m3 = 0,08 KN/m2
-Caldana (0,04 x 1 x 1) m3/m2 x 7 KN/m3 = 0,28 KN/m2
Tra i carichi permanenti, in questo esercizio vengono inseriti anche il peso dei tramezzi e quello degli impianti che sono già stabiliti e sono espressi in KN/m2.
-Impianti 0,5 KN/m2
-Tramezzi 1 KN/m2
qa: 2 KN/m2
-Civile abitazione 2 KN/m2
Una volta trovati questi valori dei carichi, essi vanno combinati e moltiplicati a dei coefficienti (che cambiano a seconda dello stato limite preso in considerazione) ed otteniamo così il carico in un metro quadro di solaio.
qtot (KN/m2) = 1,3qs + 1,5qp + 1,5qa
Ciò che interessa a noi è sapere quant’è il carico lungo la trave presa in esame che si esprime in KN/m e di conseguenza ci serve di individuare la sua area di influenza (A= i x l).
Attraverso una serie di passaggi si arriva a definire il qu (carico agente sulla trave allo stato limite ultimo) espresso in KN/m e che il foglio Excel per il dimensionamento della trave ci dà in automatico una volta inseriti i valori dei carichi del solaio e quelli dell’interasse e della luce.
A questo punto il foglio Excel calcola il momento massimo agente sulla trave che non è altro che M= qul2/2 se consideriamo la trave come una mensola.
Il passo successivo è quello di scegliere il tipo di legno da utilizzare per la sezione da progettare, in questo caso viene scelto il legno lamellare ed una classe GL24h che ha una resistenza caratteristica a flessione di 24N/mm2 (fm,k).
Dalla resistenza caratteristica si passa a quella di progetto inserendo alcuni fattori, uno è il kmod , un coefficiente tabellare che diminuisce la resistenza del materiale e che tiene conto anche della durata del carico e che assumiamo sia 0.80; ed un coefficiente parziale di sicurezza che dipende dal tipo di legno scelto e che assumiamo sia 1,45.
Una volta inseriti questi valori nel foglio Excel, bisogna scegliere la base della sezione progettata che assumiamo essere 20 cm. A questo punto il foglio calcola hmin che la sezione deve avere e di conseguenza possiamo fissare l’altezza H della nostra trave che decidiamo essere di 50 cm.
In questo caso, trattandosi di una mensola non basta scegliere solo la dimensione della nostra sezione ma andrà fatta la verifica a deformabilità dell’elemento strutturale, ossia bisognerà verificare l’abbassamento massimo della mensola in rapporto alla luce. Tale verifica va fatta allo Stato Limite d’Esercizio per cui bisognerà ricombinare i carichi con i coefficienti allo stato limite d’esercizio che il foglio Excel calcola in automatico. Si inserirà poi il valore del Modulo elastico del materiale ed in automatico il foglio calcolerà il Momento d’Inerzia (bh3/12) e l’abbassamento massimo consentito Vmax che deve rimanere al di sotto di 1/250 della luce della trave. In questo caso la sezione risulta verificata.
DIMENSIONAMENTO E VERIFICA DI DEFORMABILITà DI UNA MENSOLA IN ACCIAIO
Si disegna innanzitutto la pianta di carpenteria di un edificio la cui maglia strutturale si compone di travi(profilo IPE) e pilastri (profilo HE); si individua la trave maggiormente sollecitata e la sua area di influenza in modo da evidenziarne il suo interasse.
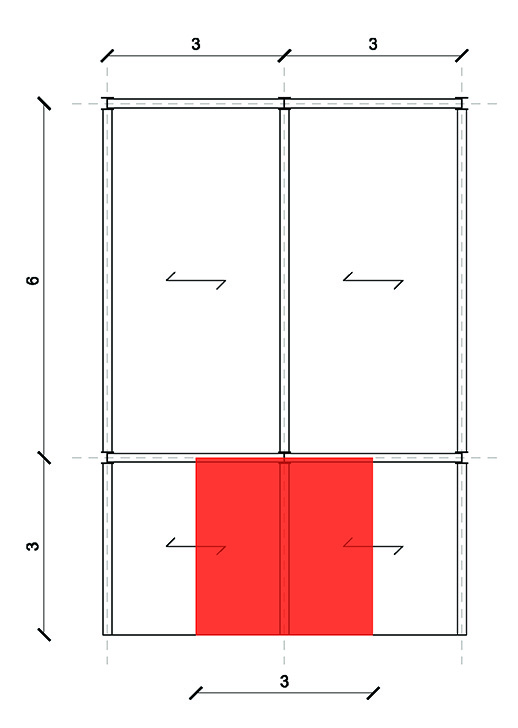
Una volta individuata la pianta di carpenteria si passa alla scelta del solaio tipo che grava sulla trave presa in esame. Ognuno dei materiali che compone la stratigrafia del solaio ha un suo spessore ed un suo peso specifico:
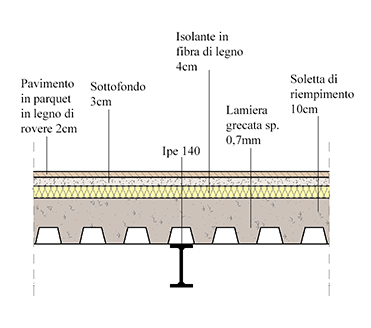
Materiale: Sp. Peso specifico:
-Pavimento in legno di rovere 2cm 820Kg/m3 = 8,2KN/m3
-Sottofondo 3cm 1800Kg/m3 = 18KN/m3
-Isolante in fibra di legno 4cm 200Kg/m3 = 2KN/m3
-Lamiera grecata Hi-Bond 0,7mm 0,09KN/m2
-Soletta di riempimento H 10 cm 190Kg/m2 = 1,9 KN/m2
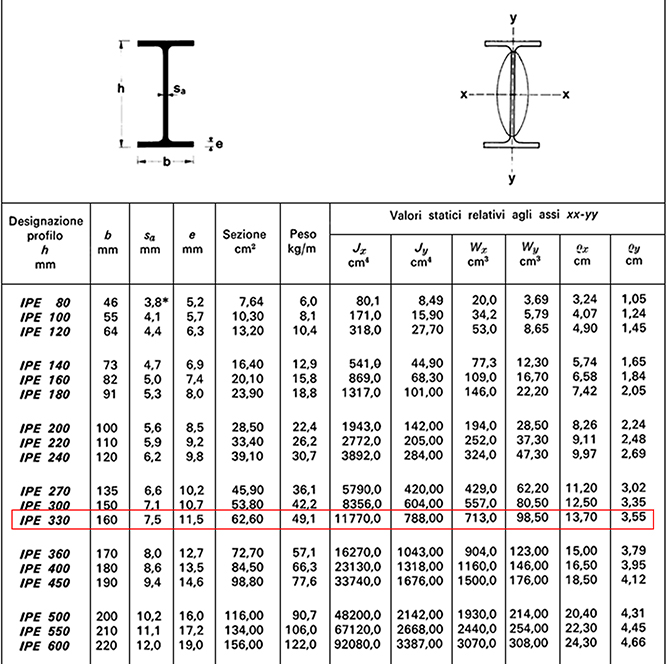
-IPE 140 A=16,40cm2 78,5KN/m2
Conoscere lo spessore ed il peso specifico dei materiali che compongono il solaio ci serve per analizzare i carichi che gravano sulla trave che vogliamo dimensionare. Tali carichi si dividono in carichi strutturali qs (KN/m2) nei quali si includono tutti gli elementi che hanno una funzione portante, carichi permanenti qp (KN/m2) nei quali si includono tutti quegli elementi che non hanno funzione portante; carichi accidentali qa (KN/m2) che dipendono dalla funzione che svolge l’edificio.
L’analisi dei carichi del solaio ci serve per determinare il carico di progetto che agisce sulla trave da dimensionare e che si esprime in KN/m.
Quasi tutti i materiali del solaio sono espressi in KN/m3; noi vogliamo sapere quanto volume occupa ogni materiale in un metro quadro di solaio per cui si procede in questo modo:
qs: 1,9 + 0,09 + 0,1256 = 2,12KN/m2
-Soletta di riempimento 1,9KN/m2
-Lamiera grecata Hi-Bond 0,09KN/m2
-IPE 140 (0,0016 x 1 ) m3/m2 x 78,5KN/m3 = 0,1256KN/m2
qp: 0,16 + 0,54 + 0,08 + 0,5 + 1 = 2,3KN/m2
-Pavimento in legno di rovere (0,02 x 1 x 1) m3/m2 x 8,2 KN/m3 = 0,16 KN/m2
-Sottofondo (0,03 x 1 x 1) m3/m2 x 18 KN/m3 = 0,54 KN/m2
-Isolante in fibra di legno (0,04 x 1 x 1) m3/m2 x 2 KN/m3 = 0,08 KN/m2
Tra i carichi permanenti, in questo esercizio vengono inseriti anche il peso dei tramezzi e quello degli impianti che sono già stabiliti e sono espressi in KN/m2.
-Impianti 0,5 KN/m2
-Tramezzi 1 KN/m2
qa: 2 KN/m2
-Civile abitazione 2 KN/m2
Una volta trovati questi valori dei carichi, essi vanno combinati e moltiplicati a dei coefficienti (che cambiano a seconda dello stato limite preso in considerazione) ed otteniamo così il carico per un metro quadro di solaio.
qtot (KN/m2) = 1,3qs + 1,5qp + 1,5qa
Ciò che interessa a noi è sapere quant’è il carico lungo la trave presa in esame che si esprime in KN/m e di conseguenza ci serve di individuare la sua area di influenza (A= i x l).
Attraverso una serie di passaggi si arriva a definire il qu (carico agente sulla trave allo stato limite ultimo) espresso in KN/m e che il foglio Excel per il dimensionamento della trave ci dà in automatico una volta inseriti i valori dei carichi del solaio e quelli dell’interasse e della luce.
A questo punto il foglio Excel calcola il momento massimo agente sulla trave che non è altro che M= qul2/2 se consideriamo la trave come una mensola.
Si sceglie poi il tipo di acciaio, in questo caso S235, che ha una resistenza caratteristica allo snervamento di 235N/mm2. Dalla tensione caratteristica si passa a quella di progetto grazie all’introduzione di un coefficiente di sicurezza pari a 1,05 che abbassa la resistenza allo snervamento del materiale.
Una volta trovati tutti i valori il foglio Excel calcola il Modulo di resistenza a flessione minimo (Wx,min = Mmax/fd). Si sceglie di conseguenza un profilo IPE da tabella che abbia un Wx immediatamente più grande del Wx,min dato da Excel e si inseriscono i valori del Momento d’Inerzia e del peso del profilo scelto.
In questo caso scegliamo un profilo IPE 330 che ha un Wx = 713cm3 , Ix = 11770cm4 ,
P = 0,49KN/m
In questo caso, trattandosi di una mensola non basta scegliere solo la dimensione della nostra sezione ma andrà fatta la verifica a deformabilità dell’elemento strutturale, ossia bisognerà verificare l’abbassamento massimo della mensola in rapporto alla luce. Tale verifica va fatta allo Stato Limite d’Esercizio per cui bisognerà ricombinare i carichi con i coefficienti allo stato limite d’esercizio che il foglio Excel calcola in automatico. Si inserirà poi il valore del Modulo elastico del materiale ed in automatico il foglio calcolerà l’abbassamento massimo consentito Vmax che deve rimanere al di sotto di 1/250 della luce della trave. In questo caso la sezione risulta verificata.
DIMENSIONAMENTO E VERIFICA DI DEFORMABILITà DI UNA MENSOLA IN CALCESTRUZZO ARMATO
Si disegna innanzitutto la pianta di carpenteria di un edificio la cui maglia strutturale si compone di travi e pilastri; si individua la trave maggiormente sollecitata e la sua area di influenza in modo da evidenziarne il suo interasse.
Una volta individuata la pianta di carpenteria si passa alla scelta del solaio tipo che grava sulla trave presa in esame. Ognuno dei materiali che compone la stratigrafia del solaio ha un suo spessore ed un suo peso specifico:
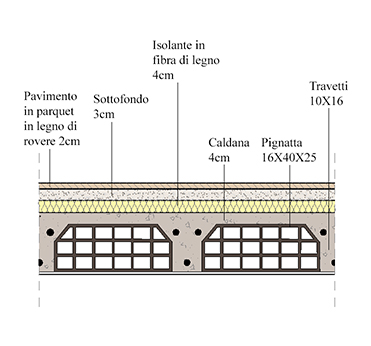
Materiale: Sp. Peso specifico:
-Pavimento in legno di rovere 2cm 820Kg/m3 = 8,2KN/m3
-Sottofondo 3cm 1800Kg/m3 = 18KN/m3
-Isolante in fibra di legno 4cm 200Kg/m3 = 2KN/m3
-Caldana 4cm 24KN/m3
-Travetti in calcestruzzo 10x16 24KN/m3
-Pignatte 16x25x40 9Kg/cad
Conoscere lo spessore ed il peso specifico dei materiali che compongono il solaio ci serve per analizzare i carichi che gravano sulla trave che vogliamo dimensionare. Tali carichi si dividono in carichi strutturali qs (KN/m2) nei quali si includono tutti gli elementi che hanno una funzione portante, carichi permanenti qp (KN/m2) nei quali si includono tutti quegli elementi che non hanno funzione portante; carichi accidentali qa (KN/m2) che dipendono dalla funzione che svolge l’edificio.
L’analisi dei carichi del solaio ci serve per determinare il carico di progetto che agisce sulla trave da dimensionare e che si esprime in KN/m.
Quasi tutti i materiali del solaio sono espressi in KN/m3; noi vogliamo sapere quanto volume occupa ogni materiale in un metro quadro di solaio per cui si procede in questo modo:
qs: 0,96 + 0,768 + 0,72 = 2,45KN/m2
-Caldana (0,04 x 1 x 1) m3/m2 x 24KN/m3 = 0,96KN/m2
-Travetti 2(0,10 x 0,16 x 1) m3/m2 x 24KN/m3 = 0,768KN/m2
-Pignatte 8 x 9Kg/m2 = 72Kg/m2 = 0,72KN/m2
qp: 0,16+0,54+0,08+1,5 = 2,28KN/m2
-Pavimento in legno di rovere (0,02 x 1 x 1) m3/m2 x 8,2 KN/m3 = 0,16 KN/m2
-Sottofondo (0,03 x 1 x 1) m3/m2 x 18 KN/m3 = 0,54 KN/m2
-Isolante in fibra di legno (0,04 x 1 x 1) m3/m2 x 2 KN/m3 = 0,08 KN/m2
Tra i carichi permanenti, in questo esercizio vengono inseriti anche il peso dei tramezzi e quello degli impianti che sono già stabiliti e sono espressi in KN/m2.
-Impianti 0,5 KN/m2
-Tramezzi 1 KN/m2
qa: 2 KN/m2
-Civile abitazione 2 KN/m2
Una volta trovati questi valori dei carichi, essi vanno combinati e moltiplicati a dei coefficienti (che cambiano a seconda dello stato limite preso in considerazione) ed otteniamo così il carico per un metro quadro di solaio.
qtot (KN/m2) = 1,3qs + 1,5qp + 1,5qa
Ciò che interessa a noi è sapere quant’è il carico lungo la trave presa in esame che si esprime in KN/m e di conseguenza ci serve di individuare la sua area di influenza (A= i x l).
Attraverso una serie di passaggi si arriva a definire il qu (carico agente sulla trave allo stato limite ultimo) espresso in KN/m e che il foglio Excel per il dimensionamento della trave ci dà in automatico una volta inseriti i valori dei carichi del solaio e quelli dell’interasse e della luce.
A questo punto il foglio Excel calcola il momento massimo agente sulla trave che non è altro che M= qul2/2 se consideriamo la trave come una mensola.
Essendo il calcestruzzo un materiale disomogeneo abbiamo bisogno di scegliere due resistenze caratteristiche; una è quella del calcestruzzo fck e l’altra è quella allo snervamento dell’armatura d’acciaio fyk. Scegliamo quindi un calcestruzzo non troppo performante con classe di resistenza C40/50 che ha una resistenza caratteristica fck = 40N/mm2 e acciaio B450A per l’armatura che ha una resistenza caratteristica di fyk = 450N/mm2.
Una volta trovate le resistenze caratteristiche possiamo ricavare le tensioni di progetto dei due materiali; il foglio Excel le calcola in automatico ma da normativa la resistenza caratteristica dell’acciaio viene divisa per un coefficiente parziale di sicurezza dell’acciaio pari a 1,15 per gli acciai d’armatura, mentre la resistenza caratteristica del calcestruzzo viene moltiplicata per un coefficiente di riduzione della sicurezza pari a 0,85 e poi divisa per il coefficiente parziale di sicurezza del calcestruzzo pari a 1,5.
Si sceglie la base della trave che in questo caso decidiamo di essere di 20 cm ed in automatico il foglio Excel calcola l’altezza utile della trave hu e l’altezza minima della trave Hmin che comprende anche 5cm di copriferro (distanza tra il baricentro dell’armatura ed il filo del calcestruzzo teso). La sezione viene ingegnerizzata e si sceglie così un’altezza della trave pari a 50cm.
In questo caso, trattandosi di una mensola non basta scegliere solo la dimensione della nostra sezione ma andrà fatta la verifica a deformabilità dell’elemento strutturale, ossia bisognerà verificare l’abbassamento massimo della mensola in rapporto alla luce. Tale verifica va fatta allo Stato Limite d’Esercizio per cui bisognerà ricombinare i carichi con i coefficienti allo stato limite d’esercizio che il foglio Excel calcola in automatico. Si inserirà poi il valore del Modulo elastico del materiale ed in automatico il foglio calcolerà il Momento d’Inerzia (bh3/12), il peso proprio della sezione da inserire nel qu (2,50KN/m) e l’abbassamento massimo consentito Vmax che deve rimanere al di sotto di 1/250 della luce della trave. In questo caso la sezione risulta verificata.
f.1
f.2
f.3
f.4
f.5
f.6
f.7
f.8
f.9
Per le aste compresse, bisogna far fronte al problema della stabilità. Di conseguenza il dimensionamento viene effettuato considerando NCRIT = π2 E Imin / λ02 , dove λ0 = β l. β in questo caso è pari ad 1, poichè le aste possono essere considerate come delle travi appoggiate, mentre l è pari a 2. Il materiale è acciaio S235 con modulo di resistenza pari a 21000 MPa. 
CONCLUSIONE 
