STRUTTURA RETICOLARE 3D IN ACCIAIO
Obiettivo: disegnare il modello tridimensionale di una struttura reticolare in acciaio, vincolarla, caricarla e calcolare N, lo sforzo normale di ogni asta componente la struttura. (con T=0, M=0 perchè le aste reticolari sono soggette solo a trazione e compressione.
Per fare ciò utilizzo SAP2000, un programma che utilizza gli elementi finiti fondato sulla Teoria di Bernulli.
1_ disegno una griglia cubica:
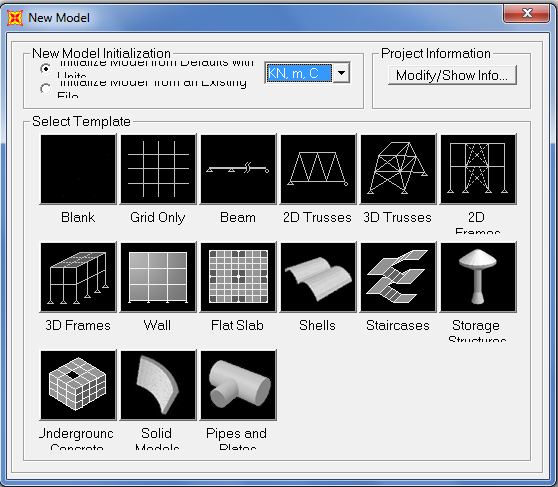
_file/new model
imposto l’unità di misura in KN,m,C
_grid only
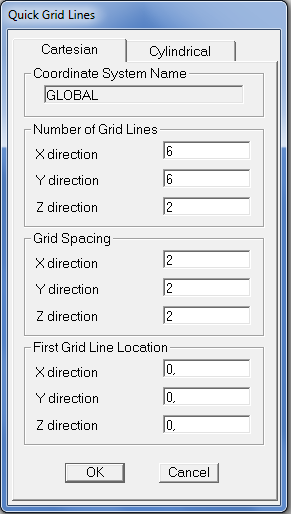
considerando il piano cartesiano con Z = gravità
number of grid line (da quante rette deve essere composta la griglia)
X (= quante rette X=n) = 6
Y (=quante rette Y=n) = 6
Z (quante rette Z=n) = 2
Grid spacing (quanto spazio vi è tra le rette che compongono la griglia, quindi volendo fare una griglia cubica X=Y=Z)
X (= spazio tra le rette X=n)= 2 m
Y(= spazio tra le rette Y=n)= 2m
Z(= spazio tra le rette Z=n)= 2m
First grid line location (centro)
X = 0
Y= 0
Z= 0
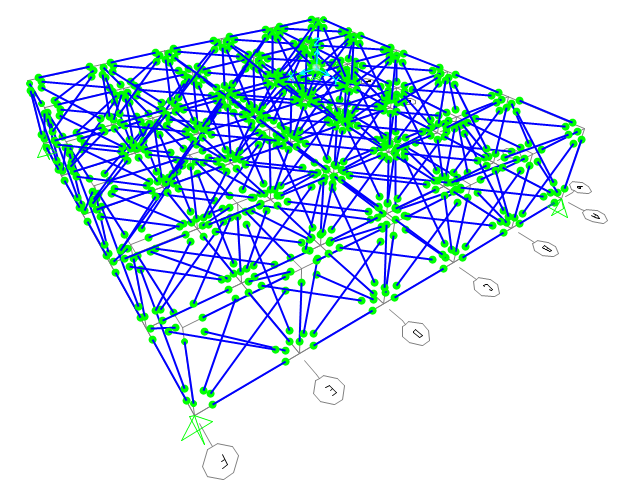
2_ ogni faccia della griglia dovrà essere controventata
Draw/frame e disegno un cubo controventato
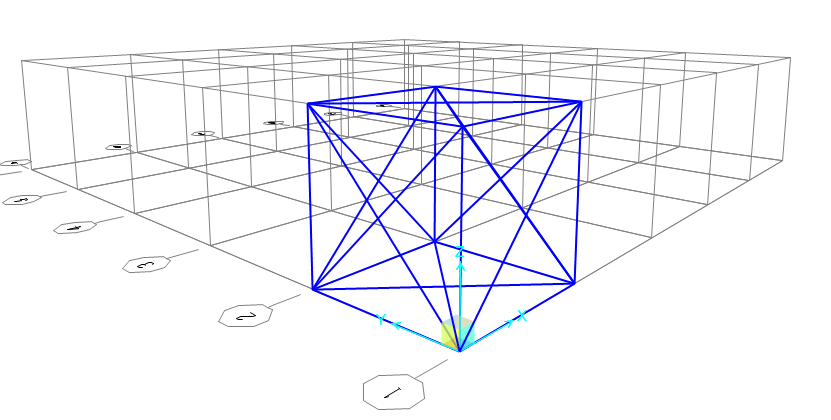
P.S. Per vedere se ho linee sovrapposte seleziono la struttura e
edit /merge duplicates/ok
2_ devo copiare il cubo controventato su tutta la griglia
_seleziono tutte le facce del cubo che voglio copiare tranne quella in comune tra esistente e la copia, per evitare che si creino linee sovrapposte e con il tasto:
Ctrl+c/ Ctrl+v specifico di voler un secondo elemento lungo l’ asse X /Y oltre a quello esistente
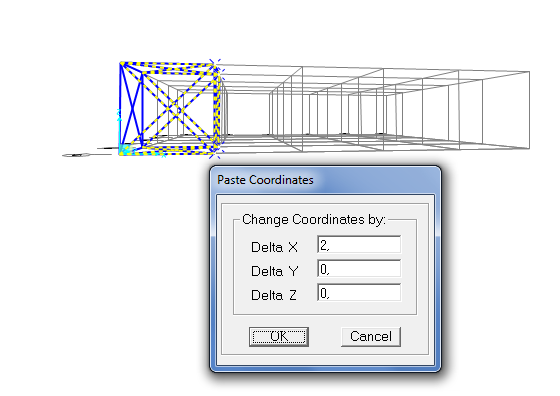
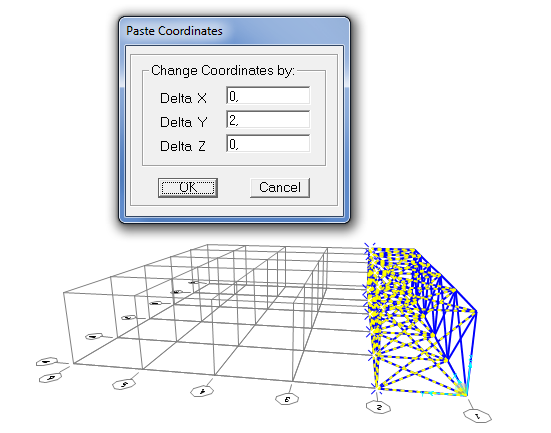
Adesso la mia griglia è completa.
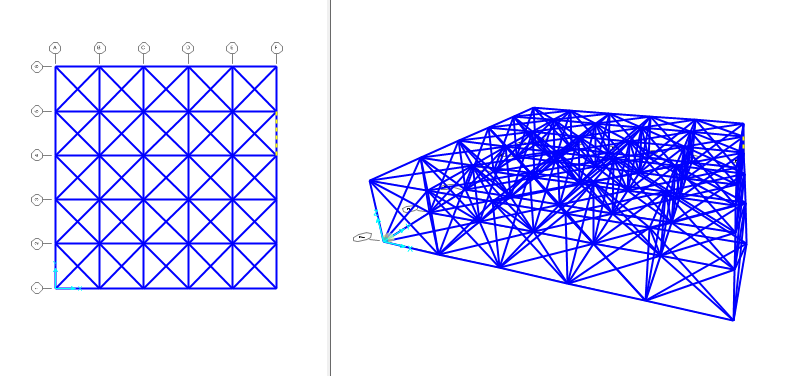
3_ controllo che tutti i nodi siano uniti:
_seleziono tutta la struttura
Edit/Edit Points/Merge Joints/0,1/ok
4_ Assegno I vincoli esterni
Voglio assegnargli 4 cerniere
_seleziono i punti in cui voglio inserirle e con:
assign/joint/restraints/ scelgo la cerniera/ok
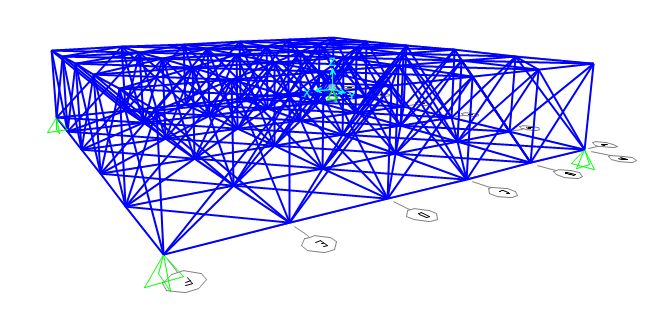
Ho messo degli appoggi alla struttura.
5_ assegno i vincoli interni alle aste
_seleziono tutta la struttura
Assign/frame/releases (spunta su moment 2-2 e moment 3-3)
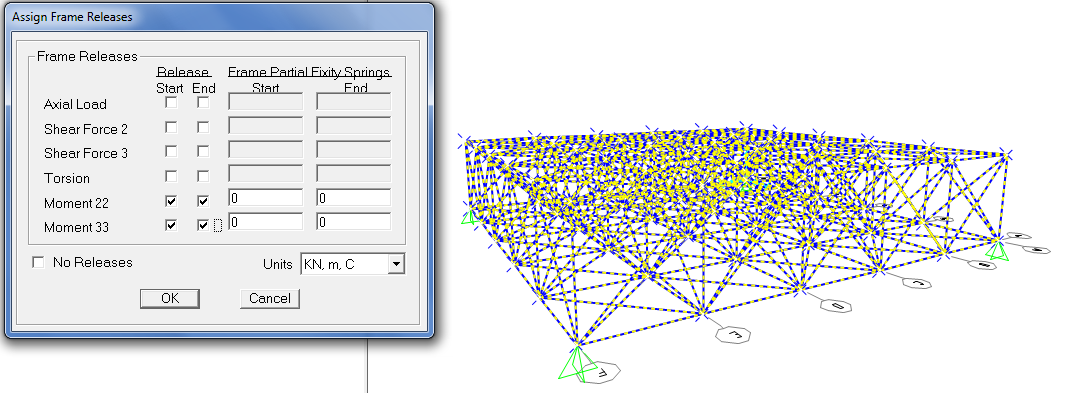
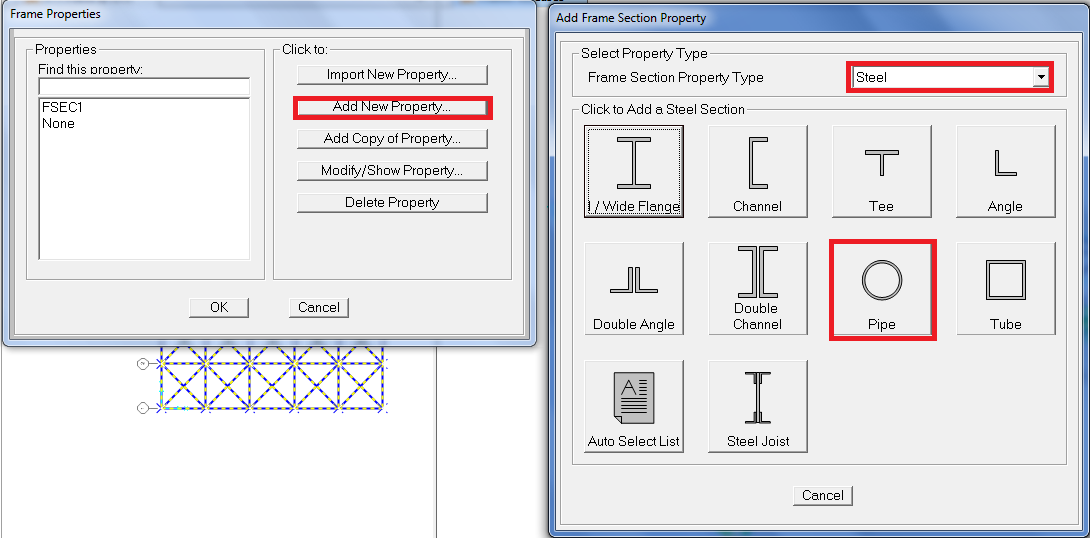
SCELGO IL PROFILO DA UTILIZZARE
6_ voglio che la mia struttura sia composta da tubolari in acciaio.
_seleziono tutta la struttura e con il comando:
assign /frame/frame sections / add new property/ PIPE section /gli do un nome e l’ok
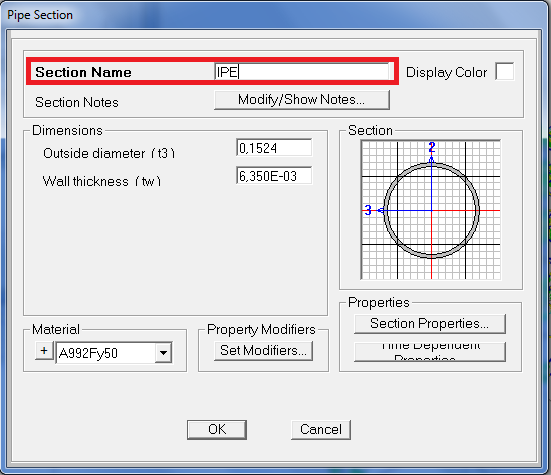
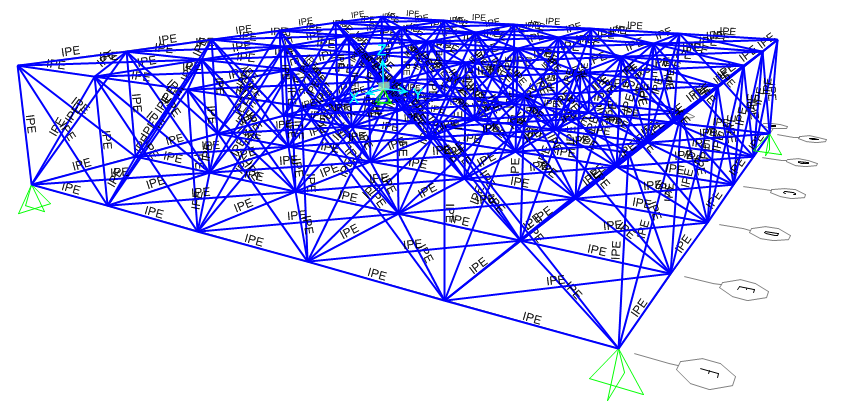
APPLICO DELLE FORZE CONCENTRATE
7_ devo prima CREARE la forza che voglio concentrare ai nodi senza considerare il peso proprio:
define/load patterns/chiamo questa forza “F”/self weight mutiplier=0/ add new load pattern/ok
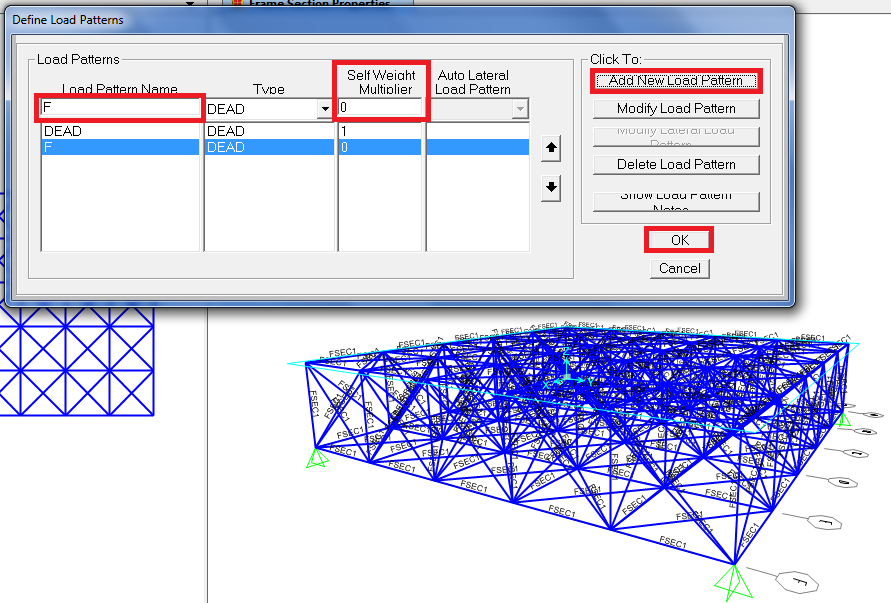
8_devo ASSEGNARE il carico che ho appena creato:
_dove devo assegnarlo? Ovviamente sulla parte superiore della struttura, quindi la vado a selezionare (lo posso fare direttamente dalla vista top)
Assign/joint load/forces /carico il nome della forze che ho appena creato “F”
Force global Z = - 150 (perche voglio una forza concentrata nei nodi di intensità pari ad 150 kN verso il basso).
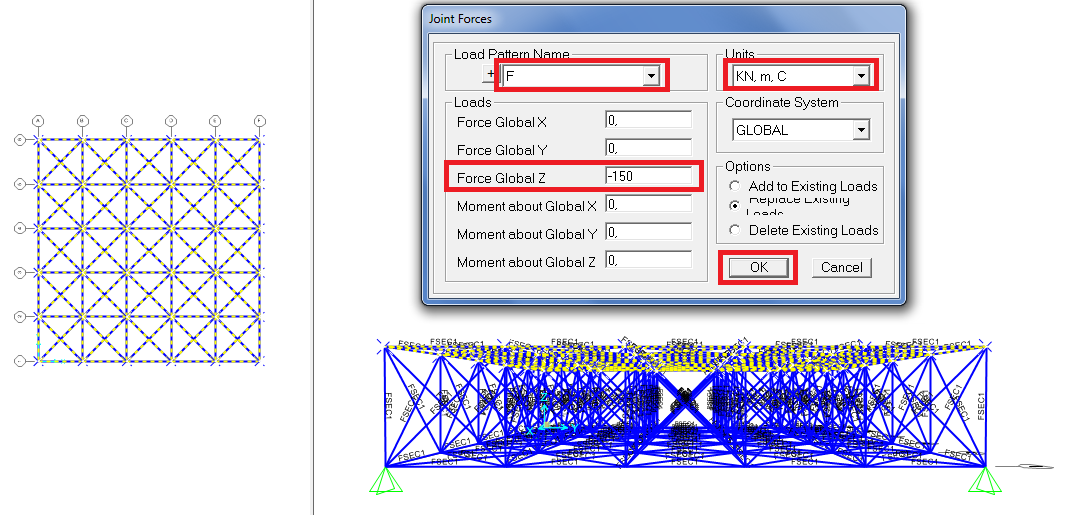
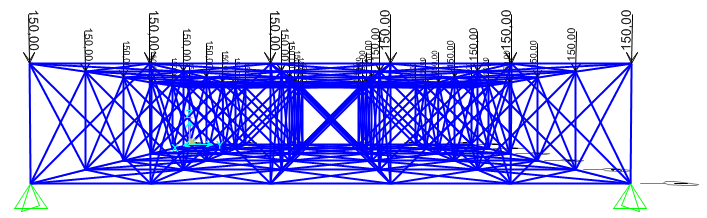
Adesso la mia struttura è caricata.
ANALISI GRAFICA DELLA DEFORMATA
Creo una nuova cartella nel computer
9_ click su play e avvio l’ analisi
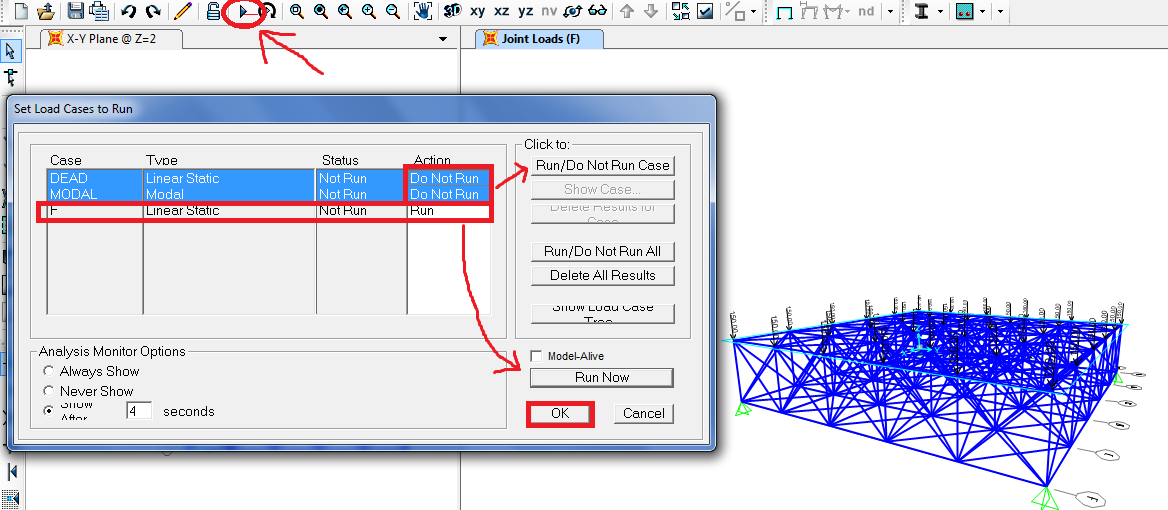
10_Non avendo considerato il peso proprio la struttura sarà così deformata:
show /deformed shape /
spunto “wire shadow” se voglio vedere contemporaneamente come era e come è la struttura.
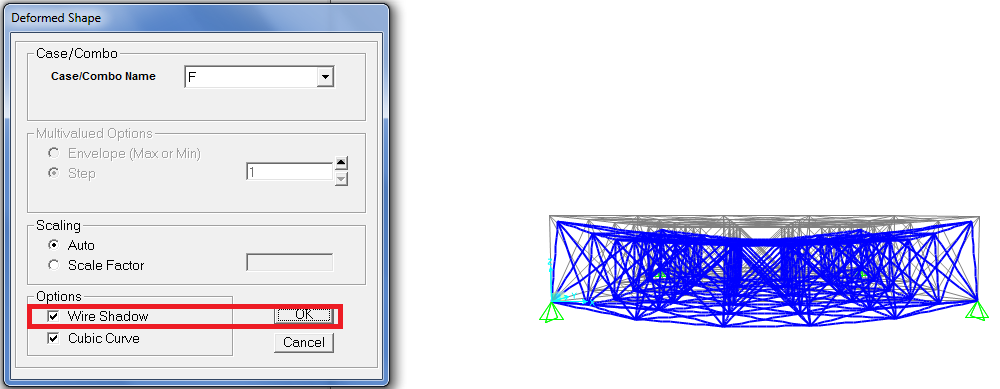
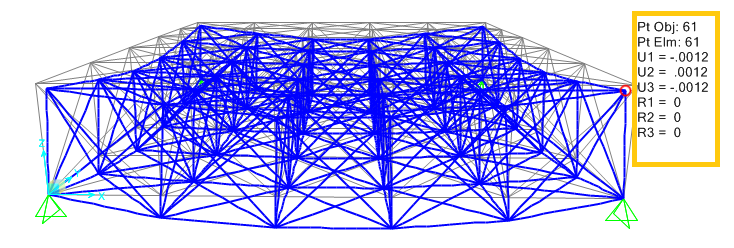
_posizionandomi con il mouse in uno dei nodi leggo di quanto si abbassa in quel punto.
ANALISI - SFORZO NORMALE
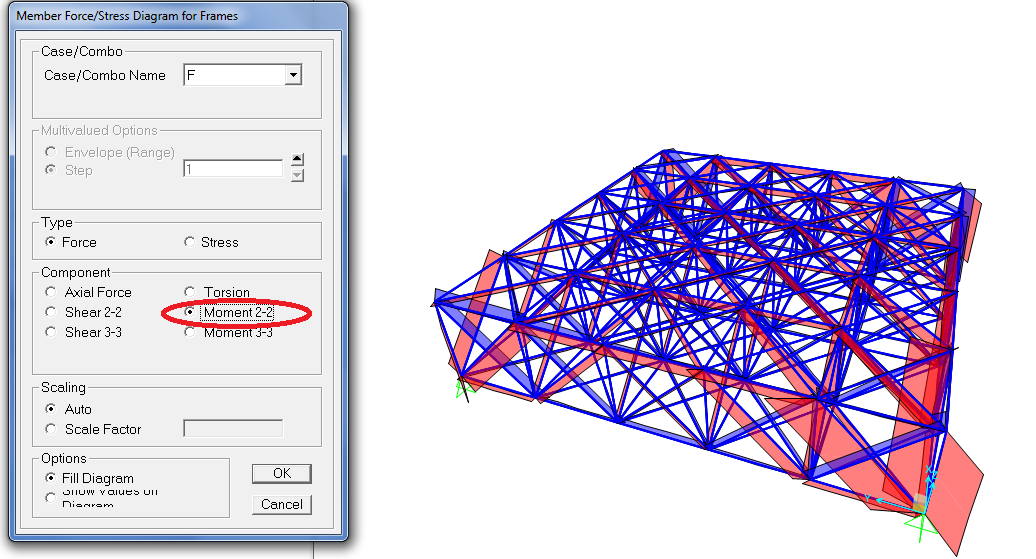
11_ show Forces/Stresses /frame
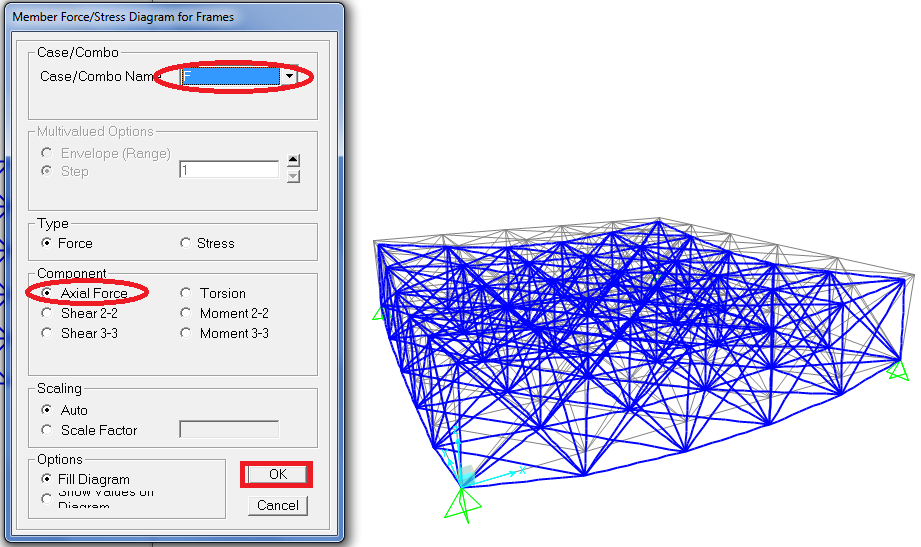
ANALISI GRAFICA DEGLI SFORZI NORMALI
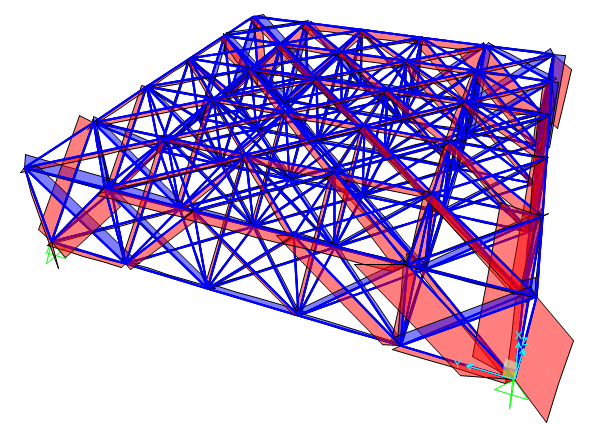
Per accertarmi che tutto sia OK verifico che i momenti siano nulli!
FILE EXCEL
12_Per conoscere con precisione quanto vale lo sforzo Normale su ogni asta che compone la struttura,SAP mi fornisce un file Excel molto utile:
Display/show tables/Analysis Results/select load patterns/ seleziono la “F”/ok
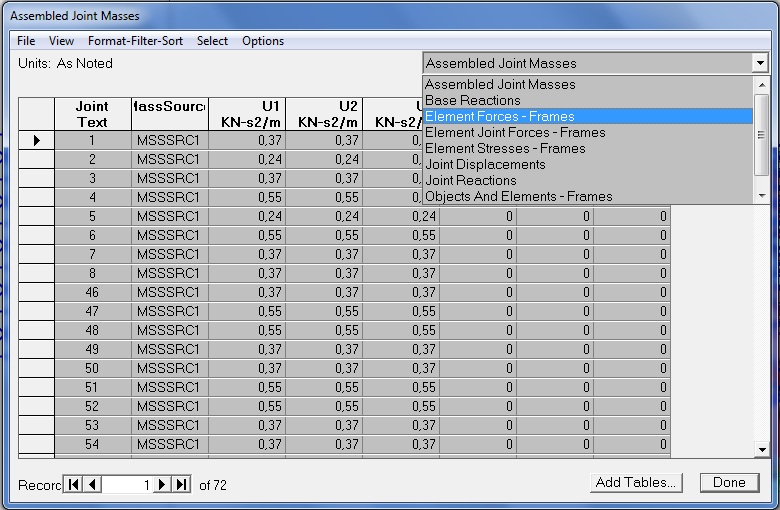
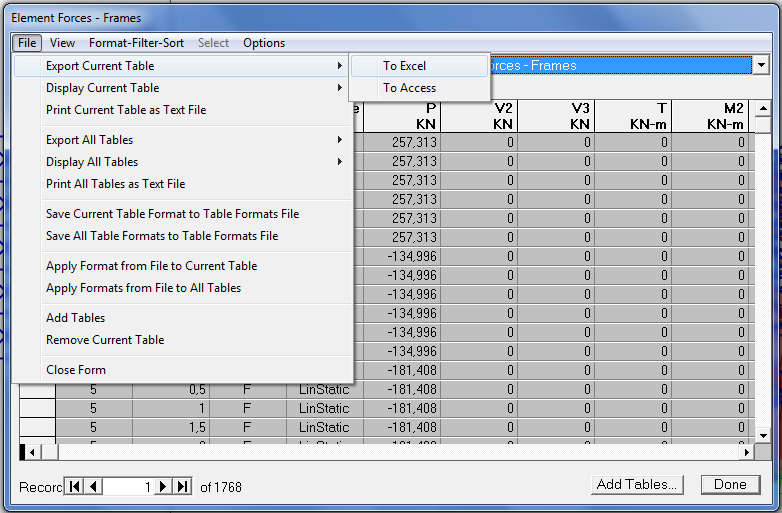
13_ ricavato il foglio Excel lo pulisco eliminando I valori non necessari al calcolo, ciò che mi serve è:
n° numero delle aste/frame/station/P
essendo un cubo considero solo le aste con L=2 m e diagonale pari a L=2,82843m.
14_ ulteriore verifica: tutti i valori dopo P devono essere nulli! Se si posso cancellarli, altrimenti ho sbagliato qualcosa!
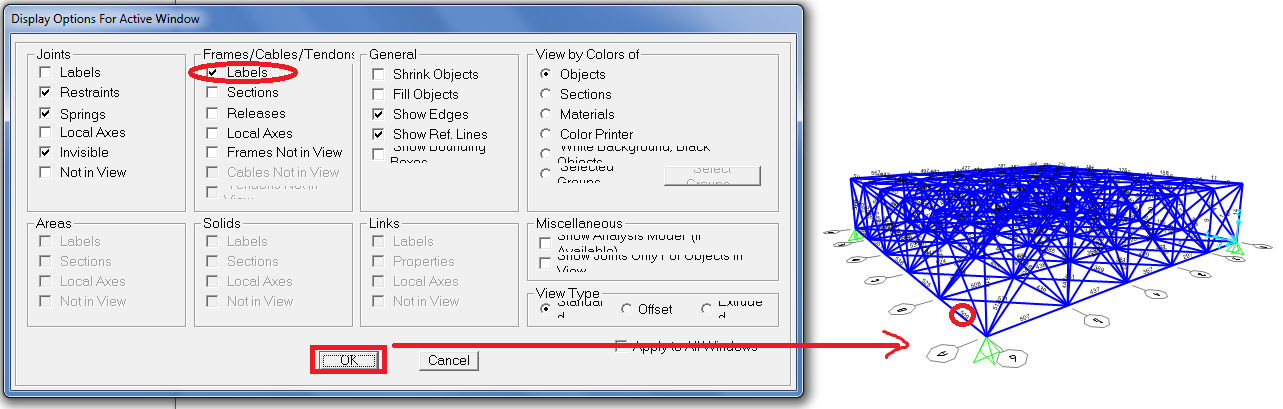
Tornando su SAP “click sul tasto della spunta” e con il comando Frame/ Labels posso vedere il numero di ciascuna asta cosi da poterla identificare sul foglio excel.
SIGNIFICATO DELLE VOCI DEL FOGLIO EXCEL:
PRIMA COLONNA: numero delle aste
FRAME: il “nome” delle aste / come vengono individuate su SAP
STATION:mi dice i passi (ogni 50 cm) come se le aste venissero suddivise in segmenti di 50 cm
P: N, quanto vale lo Sforzo Normale ad ogni frame (ogni 50 cm) ma ovviamente, essendo aste reticolari, N sarà costante! Quindi per ogni asta mi interessa solo un valore di N, quello relativo alle aste che compongono la mia reticolare 3D con L=2 (aste normali) e con L=2,82843m (aste diagonali).
seleziono tutti i frame/dati/rimuovi duplicati/espandi selezione/rimuovi duplicati
PULIZIA DELLA TABELLA EXCEL:
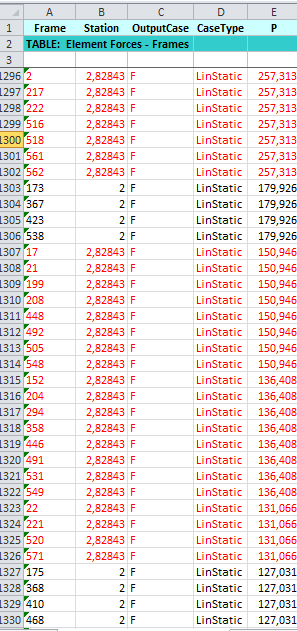
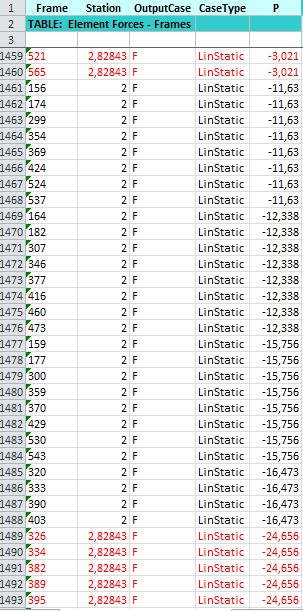
_ elimino tutte le colonne inutili e lascio solo: frame /station/outputcase/P
_Ordino station in ordine crescente (espandi selezione)
_Elimino i valori che non mi interessano e lascio solo 2 (aste normali) e 2* radice di 2(aste diagonali) = 2,82843 che evidenzio in rosso in modo da riconoscerle subito.
_ora ordino P in ordine decrescente (sforzo normale) in questo modo distinguo le aste tese da quelle compresse.
CALCOLO L’ AREA MINIMA DA SFORZO NORMALE DI TRAZIONE
_prendo i valori di N>0 (trazione) e li copio nel file excel per il dimensionamento
_fornisco alla tabella gli strumenti per calcolare fd= fyk/ ym
_ fyk (coefficiente caratteristico di snervamento) pari a 275 (valore medio)
_ ym (coefficiente di sicurezza) pari a 1,05.
_Il file individua la tensione di progetto fd e l'area minima A_min
A_min = (N / fd )* 10 (perche è in cm)
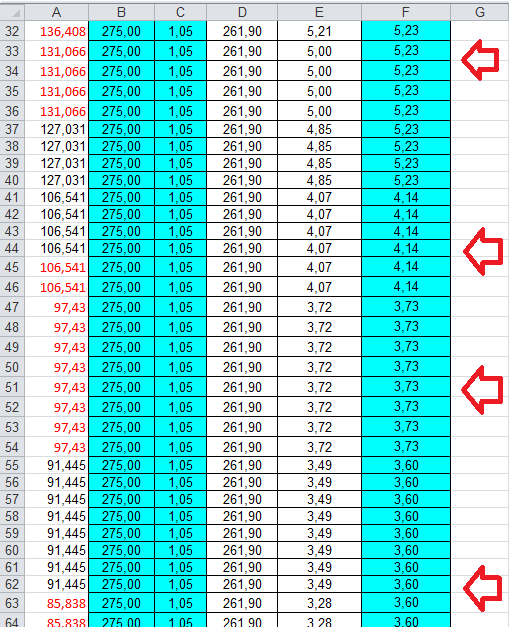
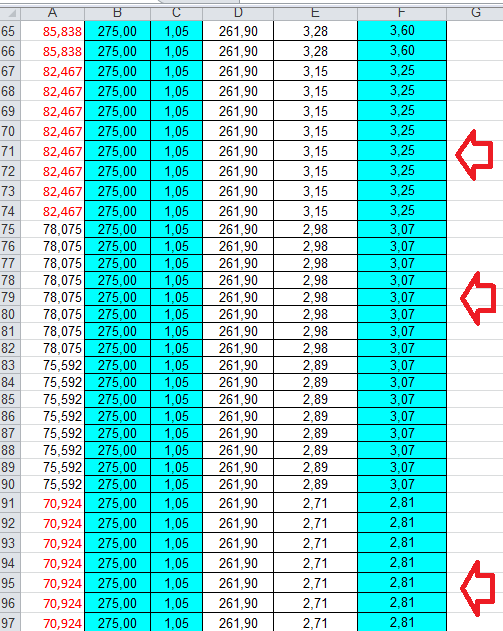
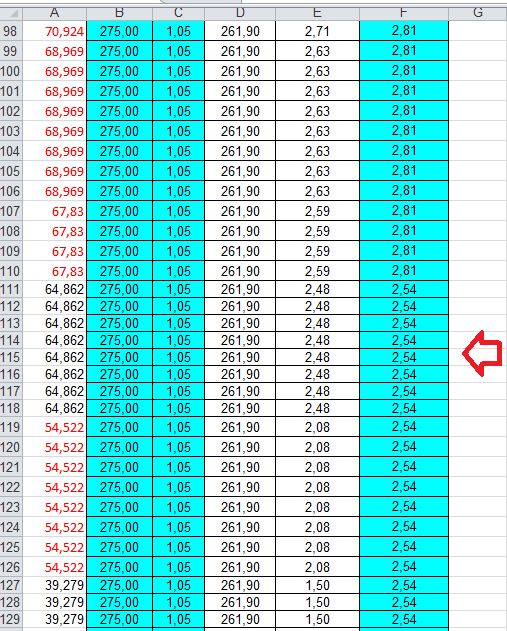
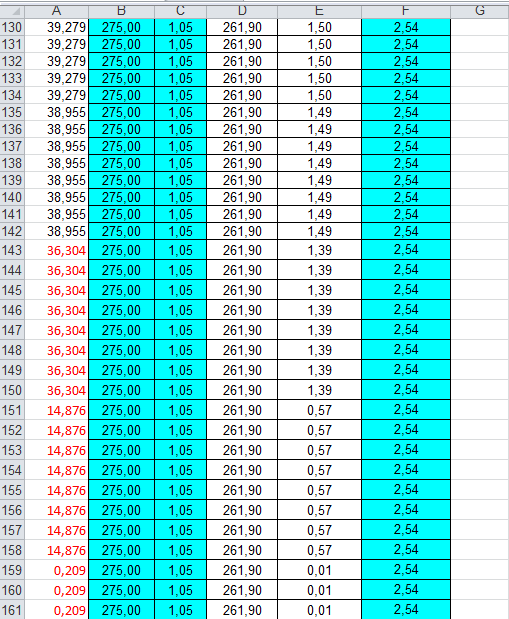
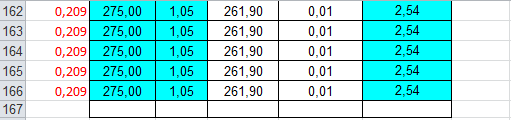
p.s. nota che l’ area minima è inversamente proporzionale alla tensione!
Consultando le tabelle dei valori standard dei profili metallici in produzione INGEGNERIZZO ricercando il valore dell’ area A_dsign disponibile immediatamente maggiore di A_min che il foglio Excel ha ricavato (lo faccio per ogni singola asta).
_Dopo averle ordinate in ordine decrescente individuo subito l’ asta maggiormente sollecitata e il valore dello sforzo normale maggiore, cosi da poter scegliere il profilo adatto a tutte le aste sottoposte a trazione che compongono la reticolare spaziale:
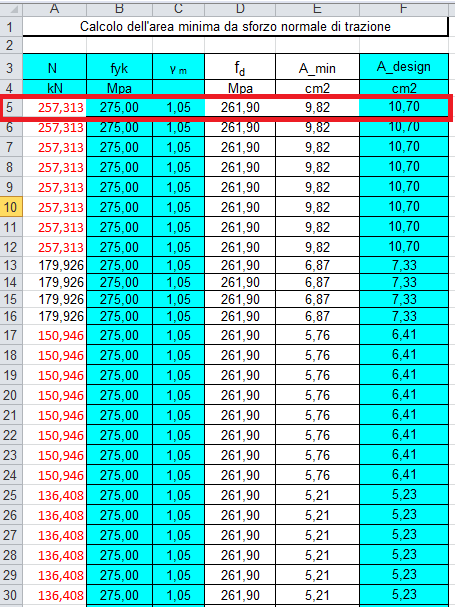
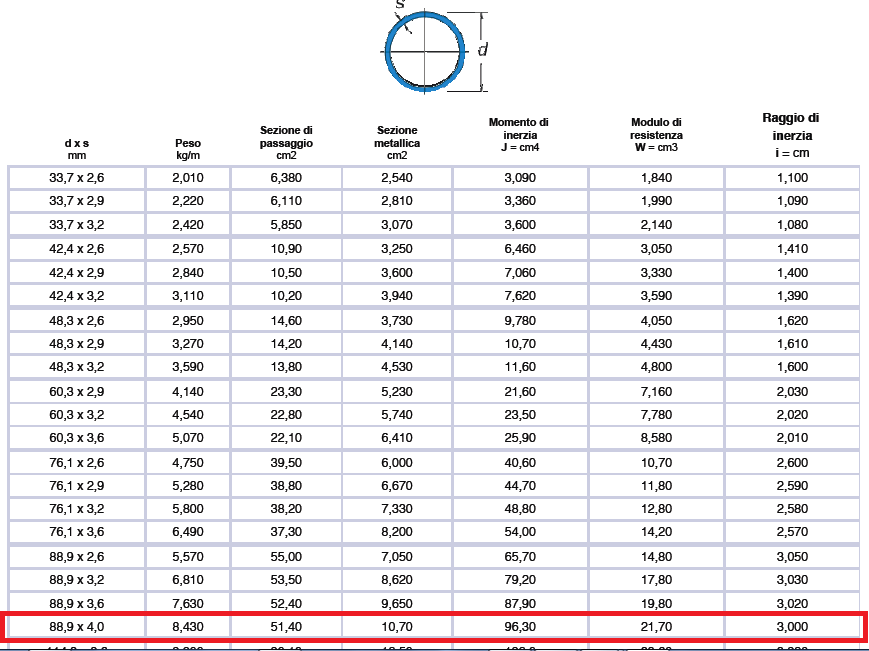
Per le aste a trazione vado a scegliere il profilo: A =10,70cm2 ; dxs= 88,9 X 4,0mm
VERIFICA :
σ<fd = N/A<fd
Considerata l’asta più sollecitata: N= 257,313KN
N/A =257313/ 1070 = 261,90 N/mm²
fd = 261,90MPa
ok : N/A < fd =240,47 N/mm² < 261,90MPa è VERIFICATA!
COMPRESSIONE
Per le aste compresse si devono considerare alcuni concetti fondamentali:
-la natura dei carichi di spostare il loro punto di applicazione nello stesso verso della forza che esercitano.
-Quando N raggiunge il valore dello sforzo normale critico euleriano si innesca improvvisamente una crisi: l’asta sbanda stantaneamente, o meglio si flette intorno all’ asse della sezione con raggio minimo d’ inerziza
N=Ncrit
Ncrit= 3,14 EImin/(βl)2 (βcoefficiente che dipende dalle condizioni di vincolo nella direzione dello sbandamento)
Ncrit= 3,14 EImin/(βl)2
OSSERVAZIONI:
- Ncrit e 3,14 EImin sono direttamente proporzionali quindi se Imin>>> ne segue che Ncrit>>>
- devo quindi agire sulla lunghezza dell’ asta, NON POSSO FARLA TROPPO SNELLA!
- β=l0 distanza tra i 2 punti di flesso 7 lunghezza libera di inflessione
- RAGGIO D’ INERZIA:
Imin/A = L4/L2= L2= (radice) L2= c
(radice)(Imin/A) = L =ρmin
con ρmin raggio d’ inerzia minimo
Imin/A = ρmin2 segue Imin = A ρmin2
Sostituendo a Ncrit= 3,14 EImin/(βl)2
Ncrit= 3,142 EA ρmin2 /(βl)2
Β=l0
Ncrit= 3,142 EA ρmin2 /( l0)2 =3,14 EA/( l0/ ρmin)= 3,14 EA/ λ
dove λ= SNELLEZZA =rapport tra l’ altezza e la sezione.
Quindi: Ncrit=3,14 EA/ λ
Si noti che la snellezza (λ) è inversamente proporzionale a Ncrit , vale a dire che meno l’ asta è snella e più è grande Ncrit (quindi è irragiungibile!!).
IL PROGETTO SI DIVIDE IN 3 FASI:
1_Calcolo dell'area minima da sforzo di compressione (resistenza materiale)
_prendo ora i valori di N<0 (compressione) e li incollo nel file Excel per il dimensionamento delle aste a compressione
_ Devo trovare l’ Amin e Imin
dove: Amin = N/ fyd
quindi la tabella deve ricavarmi la tensione di progetto fyd
_Gli fornisco i dati di cui ha bisogno:
fyk (coefficiente caratteristico di snervamento) pari a 275 (valore medio)
ym (coefficiente di sicurezza) pari a 1,05.
La tabella può ora ricavare fyd = fyk/ ym e di conseguenza Amin
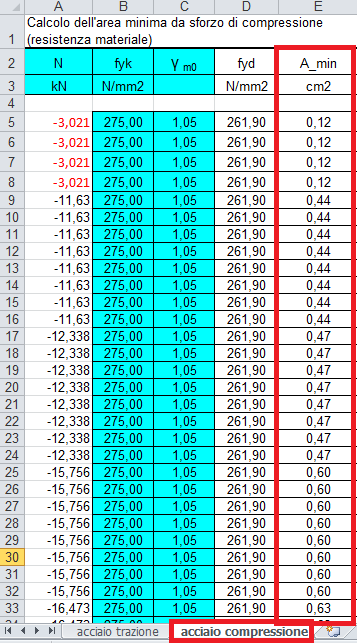
2_Calcolo dell'inerzia minima per sforzo di compressione (instabilità euleriana)
ordiniamo i valori rispetto ad N questa volta in modo crescente tale che mi trovo l’ asta maggiormente compressa in alto.
Dato che le aste compresse troppo snelle potrebbero essere soggette ai fenomeni di instabilità, per evitare che questo accada il foglio deve calcolare l'inerzia e il suo raggio attraverso alcuni dati che vado ad inserire:
E = 210000
β = 1,00
l = lunghezza delle aste (confrontando il file Excel ricavato da SAP).
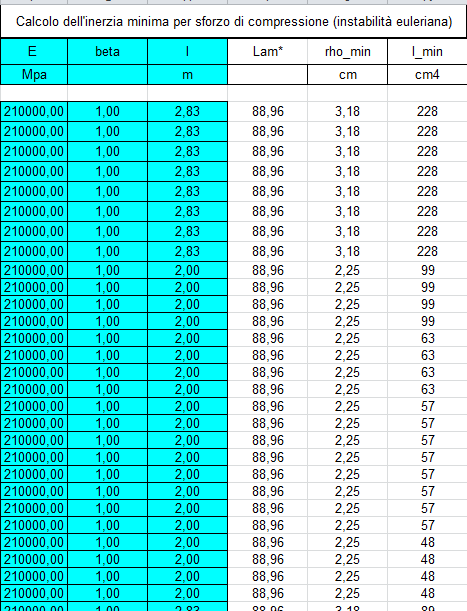
3_Ingegnerizzazione sezione e verifica snellezza per una membratura principale (< 200)
Analizzo l'asta diagonale e l'asta normale più caricate (rosso /giallo) e ingegnerizzo confrontando le tabelle:
A_design > A_min;
I_design > I_min;
ρ_design del profilo;
Devo conoscere la snellezza SNELLEZZA λ
confrontando i valori ottenuti a trazione e a compressione,si nota che l' A_min a compressione(22,57 cm2) è > di quella a trazione (9,82 cm2) quindi sarà questa quella che vado ad ingegnerizzare:
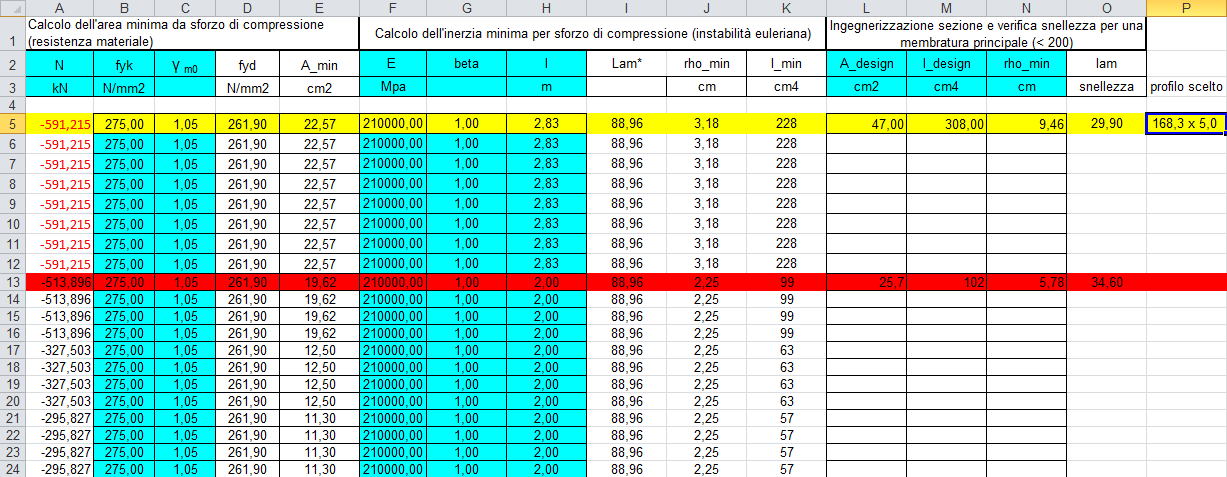
scelgo un profilato a sezione circolare dxs = 168,3 x 5,0 mm.
VERIFICA
σ<fd = N/A<fd
Considerata l’asta più sollecitata(5): N= -115,097KN
N/A = -591215/ 4700= -125,79 N/mm²
fd = 261,90MPa
ok : N/A < fd =- 125,79 N/mm² < 261,90MPa è VERIFICATA!
VERIFICO LA SNELLEZZA
La snellezza λ per essere verificata deve essere≤ 200
λ≤ 200
considerando sempre la stessa asta(5):
La sezione è verificata in quanto λ =29,90 la sua snellezza non supera il 200!