SdC(b) (LM PA)

INTRODUZIONE:

In questa esercitazione, ci occuperemo del dimensionamento di una trave a sbalzo nelle tre diverse tecnologie, ovvero il legno, l'acciaio e il calcestruzzo armato.

• Dopo aver definito la carpenteria di riferimento, individuo la trave maggiormente sollecitata e, nel rettangolo rosso, l'area di influenza di luce l=2,5m e interasse i=4m.

A questo punto posso passare all'analisi di ogni tecnologia.

Prendendo in considerazione la stratigrafia dei solai analizzati nel prima esercitazione, prendo in riferimento i carichi ivi ottenuti. [http://design.rootiers.it/strutture/node/1713]

1_STRUTTURA IN LEGNO

Il procedimento iniziale è lo stesso applicato nella prima esercitazione, quindi i valori delle prime colonne permettono di ricavare h_min, nel caso del legno e del c.a., o W_min, nel caso dell’acciaio.

 NOTA: A differenza della prima esercitazione, dove consideravamo una trave doppiamente appoggiata, in questo caso stiamo prendendo lo schema statico di una mensola, perciò il valore del momento massimo viene ricavato dalla formula: M_max= ql²/2.

ANALISI:

• ​​​q_s = 0.44 KN/m²
• q_p = 2.64 KN/m²
• q_a  = 2 KN/m²

^​Il foglio di calcolo mi fornisce il carico totale a metro lineare (qu), e, dopo aver inserito il valore della luce, il momento massimo M_max= ql²/2, trattandosi di una mensola.

• Assumo:

1.  f_m,k= 24 (legno lamellare GL 24c)                              [resistenza a flessione caratteristica]
2. K_mod = 0.80                                                             [coefficiente di durata del carico]
3. γ _m = 1.50                                                                [coefficiente parziale di sicurezza del materiale]

Con questi valori il file excel è in grado di calcolare la tensione ammissibile f_d c tramite la formula fm,k x kmod / γm.

PROGETTO: 

• Ipotizzo la base della trave pari a 25 cm. Il mio file excel sviluppa un'altezza minima Hmin che richiede di essere ingegnerizzata, data la presenza dei decimali. 
• Dopodichè, assegnando al materiale un modulo elastico E pari a 8000 Mpa, ottengo i seguenti valori:

1.  I_x  (momento di inerzia)  ricavato dalla formula b*h³/12
2. q_e  il carico incidente, dove, a differenza dell'acciaio e del cls armato, non inserisco il peso proprio della trave perché si tratta di un materiale leggero (quindi è trascurabile)

Risulta necessario effettuare la verifica a deformabilità controllando che l’abbassamento massimo del profilo, analizzato in rapporto alla sua luce, non sia tale da deformare la struttura, limitandone l’uso. Per questo la verifica viene fatta facendo riferimento alla stato limite d’esercizio SLE.

v_max l'abbassamento massimo ed il suo rapporto con la luce l/v_max che da normativa deve essere l/ v_max ≥ 250 (valore valido per i solai in generale).

_​

 ANALISI:

• ​​​q_s = 2.46 KN/m²
• q_p = 2.97 KN/m²
• q_a  = 2 KN/m²

^​Il foglio di calcolo mi fornisce il carico totale a metro lineare (qu), e, dopo aver inserito il valore della luce, il momento massimo M_max= ql²/2, trattandosi di una mensola.

• Assumo:

1. f_yk= 450 MPa                                   [tensione di snervamento]
2. f_ck = 35 MPa                                    [valore caratteristico di resistenza cilindrica]

Con questi valori il file excel è in grado di calcolare la tensione di progetto del cls f_yd e dell'acciaio f_cd .

PROGETTO: 

• Ipotizzo la base della trave pari a 25 cm e un copriferro δ di 5 cm. Il mio file excel sviluppa un'altezza minima Hmin che, come sopra, ingegnerizzo.
• Dopodichè, assegnando al materiale un modulo elastico E (informazione relativa al materiale)  pari a 8000 Mpa, ottengo i seguenti valori:

1.  I_x (informazione relativa alla geometria) ricavato dalla formula b*h³/12
2. q_e  il carico incidente, dove inserisco il peso proprio della trave
3. v_max l'abbassamento massimo ed il suo rapporto con la luce l/v_max che da normativa deve essere l/ v_max ≥ 250

 ANALISI:

• ​​​q_s = 2.46 KN/m²
• q_p = 2.97 KN/m²
• q_a  = 2 KN/m²

^​Il foglio di calcolo mi fornisce il carico totale a metro lineare (qu), e, dopo aver inserito il valore della luce, il momento massimo M_max= ql²/2, trattandosi di una mensola.

• Assumo:

1. f_yk= 235 MPa                                   [tensione di snervamento]

Con questo valore il file excel mi calcola la tensione di progetto f_d dell'acciaio.

PROGETTO: 

• Attrraverso la formula M_max/f_d ottengo il valore W_min ovvero il modulo della resistenza
• Dopodichè, ingegnerizzando il valore del modulo della resistenza, ottengo i seguenti valori dalla tabella dei profili IPE standard:

1.  I_x  corrisponde a J_x nella tabella e si esprime in cm⁴
2. peso, che nella tabella è espresso in Kg/m, devo trasformarla in Kn/m moltiplicando il valore per 10^-2
3. q_e  il carico incidente, dove inserisco il peso proprio della trave
4. v_max l'abbassamento massimo ed il suo rapporto con la luce l/v_max che da normativa deve essere l/ v_max ≥ 250

​

Il profilo IPE scelto è un IPE300.

 

Questa seconda esercitazione prevede l'analisi di una travatura reticolare tridimensionale

attraverso l'uso del software SAP2000 e il suo dimensionamento grazie all'utilizzo di un foglio

Excel.

 

MODELLAZIONE 3D DELLA TRAVE E ANALISI

Scelgo di fare una trave reticolare formata da diversi cubi reticolari di lato 2 m.

La griglia sulla quale viene realizzato il modello tridimensionale varia a seconda del valore

dato a x,y e z. 

Scelgo x = 3, y = 5, z = 2  e quindi ottengo un modello formato da otto cubi di lato 2 m e con

diagonali di 2,83 m.

Assegno la cerniera come vincolo ai quattro appoggi angolari e svincolo i nodi al momento in

tutte le direzioni perchè le strutture reticolari lavorano a solo sforzo normale, di trazione o

compressione.

 

 

Scelgo poi la sezione e il materiale delle aste, in questo caso un tubolare in acciaio, e

assegno ai nodi superiori una forza F che scelgo pari a 80 KN. 

 

 

Faccio quindi partire l'analisi lineare statica della struttura sotto l'azione della forza F che ho

scelto. 

In questo modo posso vedere la struttura deformata e i diagrammi delle sollecitazioni che,

trattandosi di una trave reticolare, dovranno essere nulli per lo sforzo di taglio e il momento

flettente.

 

 

 

Ottengo quindi una tabella con i diversi valori di sforzo assiale, di trazione o compressione,

delle diverse aste e la esporto in un foglio Excel.

 

DIMENSIONAMENTO DELLE ASTE

Una volta evidenziate le aste diagonali in rosso, separo le aste sottoposte a trazione (valori

positivi di N) da quelle sottoposte a compressione (valori negativi).

 

Trazione

Per ogni asta riporto il suo valore di N e le caratteristiche dell'acciaio che ho scelto,

ovvero f_y,k = 235 MPa e γ_m = 1,05. Ottengo quindi per ognuna un area minima, in base alla

quale scelgo per ciascuna asta un profilato con area maggiore del valore ottenuto. 

 

 

Compressione

Per ogni asta riporto il suo valore di N e le caratteristiche dell'acciaio che ho scelto,

ovvero f_y,k = 235 MPa e γ_m = 1,05. Anche qui dunque ottengo per ognuna un area minima.

Diversamente dalla trazione, per la compressione bisogna considerare il fenomeno di

instabilità e quindi aggiungo il valore del modulo di elasticità dell'acciaio E = 210000 MPa e

del coefficiente beta = 1.

 

 

Ottengo quindi tre diversi valori, Lambda, Rho_min e I_min. In base ad essi posso dimensionare

le aste, scegliendo per ognuna di esse il profilato che meglio soddisfi questi tre valori e l'area

minima. 

 

L'esercitazione 3 prevedeva il dimensionamento di una trave a sbalzo, nelle 3 diverse tecnologie: Legno, Acciaio e Cemento armato.

Questo è il telaio preso in esame:

Fig.1

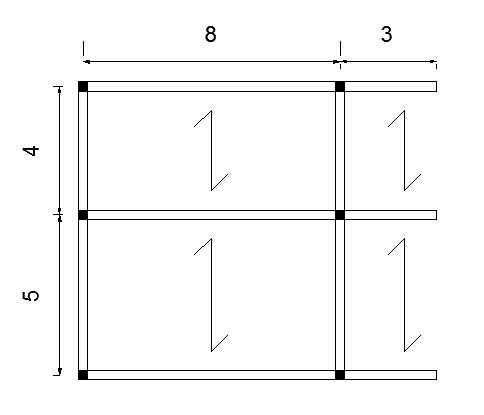
Fig.2

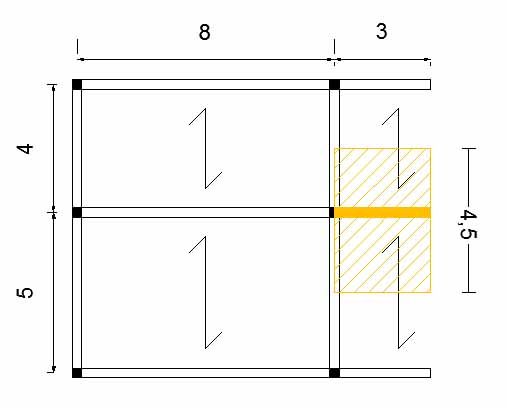
La luce= 3 m

Interasse= 4,5 m

Riprendo lo studio dei 3 solai fatto nell'esercitazione 1 e riporto qui sotto solo i carichi calcolati.

LEGNO:

CARICHI STRUTTURALI: qs

Travetto:  0.056 kn/mq

Tavolato:0,21 kn/mq

qs=(0,056+0,21) kn/mq =0,266 kn/mq

CARICHI PERMANENTI:

Pavimento: 0,2 kn/mq

Massetto: 0,72 kn/mq

Controsoffitto: 0,26 kn/mq

Tramezzi: 1 kn/mq

Impianti: 0,5 kn/mq

isolante: 0,008 kn/mq

qp=(0,2+0,72+0,26+1+0,5+0,008)kn/mq =2,688 kn/mq

CARICHI ACCIDENTALI:

Per residenze da normativa 2 kn /mq

Per uffici  da normativa 3 kn /mq

Vado ad inserire i valori appena citati nella file excel:

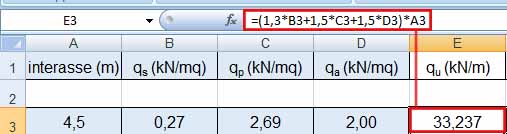
Il foglio excel mi calcola q_u  considerando i relativi coefficenti di sicurezza 1,3 per i carichi struttuali e 1,5 per i carichi permaneti e accidentali.

Trattandosi di una trave a sbalzo, M_max si calcola M_max=q_u l²/2

 inserisco ora i dati relativi al materiale ossia quello di un legno classe C24 (f_mk = 24 N/mm², K_mod = 0.8, γ_m  = 1.50) per ottenere un valore della tensione di progetto pari a f_dC = 12,8 N/mm² 

 scelgo una base di 25 cm ed ottengo una altezza minima  di 52,96 cm che ingegnerizzo a 55 cm

Ho così dimensionato una trave di base 25 cm e altezza 55 cm 

Nel caso della mensola dopo aver dimensionato la sezione, devo fare la verifica a deformabilità.

La verifica si effettua allo SLE (Stato Limite di Esercizio),poichè la verifica ha l'obbiettivo di verificare che le deformazioni siano limitate e che non compromettono il normale utilizzo della struttura.

Calcolo tramite il  foglio excel q_e  attraverso l'utilizzo di questa formula:

q_e=(G₁₊G₂+0,5x Q₁)xi=

In questo caso,non considero il peso proprio della trave, poichè il legno è un materiale leggero.

Aggiungo il valore del  modulo elastico pari a E = 8000 N/mm² ed ottengo  Ix 

Posso ora calcolare l'abbassamento massimo, che è pari a :

v_max=q_e l⁴/8Ei_x

nel mio caso l'abbassamento corrisponde a 0,65 cm 

Non mi resta che verificare che il rapporto tra la luce della trave e il suo spostamento massimo sia maggiore di 250 come da normativa.

l/v_{max >} 250

l/v_max= 461,06

quindi la trave è verificata!!!!

ripeto lo stesso esercizio più volte cambiando dei parametri, riporto qui di seguito i risultati:

ACCIAIO:

Il solaio preso in esame è composto dai seguenti carichi:

CARICHI STRUTTURALI: qs

Lamiera:  0.11 kn/mq

Getto di completamento :2,4  kn/mq

Trave secondaria: 0,16 kn/mq

qs=(0,1+ 2,4+0,16 ) kn/mq = 2,67  kn/mq

CARICHI PERMANENTI:

Pavimento: 0,2 kn/mq

Massetto: 0,72 kn/mq

Controsoffitto: 0,26 kn/mq

Tramezzi: 1 kn/mq

Impianti: 0,5 kn/mq

isolante: 0,008 kn/mq

 

qp=(0,2+0,72+0,26+1+0,5+0,008)kn/mq =2,688 kn/mq

 

CARICHI ACCIDENTALI:

Per residenze da normativa 2 kn /mq  

oppure per uffici da normativa 3 kn/mq

vado ad inserire tali valori nel foglio excel e trovo il valore di q_{u =} 47,27 kn/m

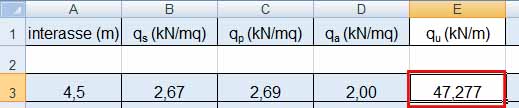
Inserendo il valore della luce dello sbalzo mi calcolo M_max= 212,746

 Ho scelto un acciaio di classe S235 che ha come  tensione caratteristica un valore  pari a  fyk=235 N/mm²

 trovato il valore di fd = 223,81 N/mm² calcoliamo il modulo di resistenza a flessione minimo uguale a Wx,min = 950,57 cm³

 vado poi  a consulatare la tabella dei profilati IPE e scelgo un IPE con W_x maggiore di quello trovato.

f_d=223,81 N/mm²    

W₂=950,57 cm³

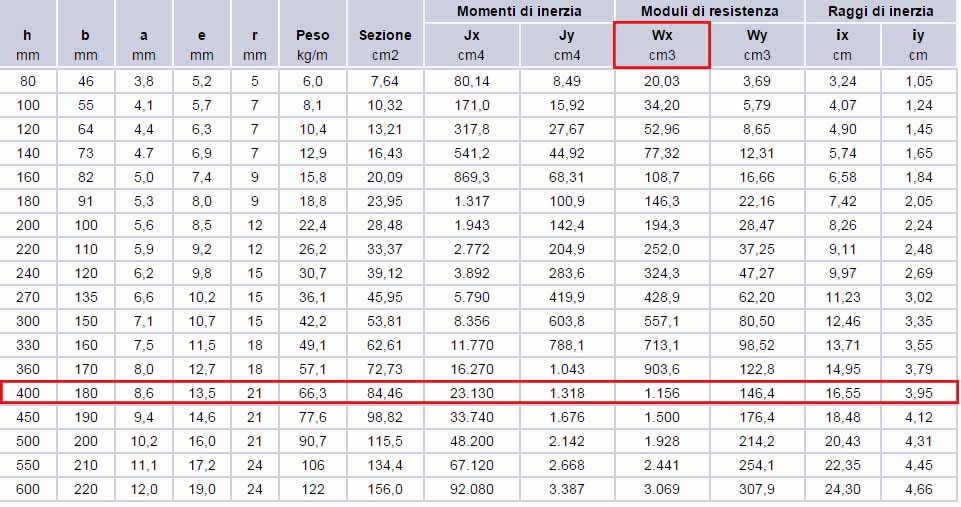
Trave IPE 400

 Inserisco il valore di I_x  ricavato dalla tabella I_x =23130 cm⁴  

Questa volta devo tener conto del peso proprio della trave che nel mio caso corrisponde a 0,66 Kn/m

Mi calcolo q_e  come avevo fatto in precedenza con il legno.

 qe= 29,28 KN/m  mi rendo conto che anche  in questo caso il progetto  è verificato poichè lo spostamento è uguale a v_max =0,610  e quindi il rapporto  I_x/ v_max >250

La trave è verificata!!!

Ripeto la stessa operazione sostituendo al carico accidentale 3 Kn /mq

Anche in questo caso la trave è verificata!!!!!!

CEMENTO ARMATO:

Il solaio che si sta studiando è formato da tali carichi

CARICHI STRUTTURALI: qs

Pignatte :  0.72 kn/mq

Travetti :0,8   kn/mq

Soletta : 1 kn/mq

qs=(0,72+ 0,8+1 ) kn/mq = 2,52 kn/mq

 

CARICHI PERMANENTI:

Pavimento: 0,2 kn/mq

Massetto: 0,72 kn/mq

isolante: 0,008 kn/mq

intonaco : 0,3 kn/mq

Tramezzi: 1 kn/mq

Impianti: 0,5 kn/mq

 

qp=(0,2+0,72+0,3+1+0,5+0,008)kn/mq =2,72888 kn/mq

 

CARICHI ACCIDENTALI:

Per residenze da normativa 2 kn /mq

Compilo la prima parte del foglio Excel con lo stesso metodo delle analisi precedenti e inserisco il valore dello sbalzo trovando così il valore del momento massimo 

Mmax= 209,95 KN*m

 Scelgo un acciaio di classe S450 ( f_yk = 450 N/mm², f_yd = 391.30 N/mm² )

Prendo un cls che abbia come tensione caratteristica f_ck = 30  N/mm² 

In questo modo trovo 3 valori:

f_cd=17N/mm²

 β=0.39

r=2.42

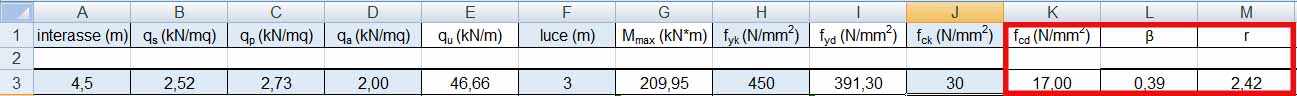
Stabilisco la base   b = 30 cm e il  copriferro di 5 cm e trovo una altezza minima h_min=54,02 cm che vado ad  ingegnerizzare, H=55 cm.

Ripetendo calcoli analoghi a quelli fatti per il legno e acciaio trovo che la trave è verificata a deformabilià.

ma non ho ancora tenuto conto del peso proprio della trave.

Quando il foglio excel tiene conto anche del peso proprio della trave, la verifica non è soddisfatta.

Provo ora ad aumentare l'H della trave e rifaccio la verifica.

Stabilendo un altezza pari a H=60 cm 

la trave è verificata!!!!

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

L'esercitazione è incentrata su modellazione, analisi e dimensionamento di una travatura reticolare.

Con il software SAP2000 ho scelto di modellarne una a base quadrangolare, il cui modulo misura 2m: ho ottenuto così una griglia tridimensionale di coordinate z=2, x=5, y=4.

Il modello è costituito da 12 cubi, ognuno dei quali formato da aste verticali ed orizzontali di 2m ed aste oblique di 2,83m.

Dopo aver controllato che non ci fossero duplicati delle aste nel modello, ho assegnato ai quattro spigoli della griglia dei vincoli esterni di tipo cerniera ed ai nodi interni dei vincoli di tipo cerniera interna, assegnando valore zero al momento nei nodi poichè una travatura reticolare lavora solo a sforzo normale.

Ho scelto poi un tubolare in acciaio ed uno schema di carico (F) per la struttura ed infine ho assegnato un carico di 80 kN per ogni nodo superiore.

A questo punto ho fatto partire l'analisi lineare statica relativa al carico F.

Ho ottenuto una deformata,

 ed uno schema dei diagrammi delle sollecitazioni che, come ho gia detto, in una reticolare è relatvo solo allo sforzo normale: di trazione o di compressione.

Ho poi esportato i valori di N relativi alle aste in un file excel, eliminando i duplicati ed evidenziando in rosso le aste diagonali per distinguerle da quelle orizzontali e verticali per procedere quindi al dimensionamento. 

Per quanto riguarda i valori di trazione, ho usato una nuova tabella in cui ho messo in realzione tali valori con le caratteristiche del materiale (fyk,Ym) per ricavare un'area minima (N/fyd) dalla quale partire per il dimensionamento delle aste usando la tabella dei profilati metallici.Per i valori di compressione ho ricavato allo stesso modo un'area minima ma prima di passare al dimensionamento ho dovuto inserire altri valori: questo perchè per la compressione bisogna tener conto dell'instabilità e considerare quindi anche la luce delle aste, la loro geometria, qundi l'inerzia ed anche l'elasticità del materiale. Una volta inseriti i valori relativi a queste caratteristiche, in particolare lambda, rho_min e I_min ho potuto dimensionare le aste tramite la tabella dei profilati.

TESSITURA DEL SOLAIO

 

                  

 

Prendo in considerazione la trave maggiormente sollecitata, ovvero la trave B.

 

SOLAIO IN LEGNO

 

Pavimento        0,4 KN/mq

Massetto          19  KN/mc

Allettamento     14  KN/mc

Tavolato            6  KN/mc

Travetti             5,3 KN/mc

 

Per determinare il Carico Strutturale q_{s e} il Carico Permanente q_p devo moltiplicare di ogni

elemento, il peso specifico per il suo volume e poi dividere per 1 mq.

Carico Strutturale 

Travetti            0,15 KN/mq

Tavolato           0,18 KN/mq

q_s = 0,15 KN/mq + 0,18 KN/mq = 0,33 KN/mq

Carico Permanente

Allettamento             0,56 KN/mq

Massetto                  0,76 KN/mq

Pavimento                0,4  KN/mq

Impianti + Tramezzi  1,5 KN/mq

q_p = 0,56 KN/mq + 0,76 KN/mq + 0,4 KN/mq + 1,5 KN/mq = 3, 22 KN/mq

Carico Accidentale

Ipotizziamo un uso residenziale quindi

q_a = 2 KN/mq

 

Inseriti questi dati nel foglio Excel, scelgo un legno lamellare GL24H che ha

f_m,k = 24,00 MPa, k_mod = 0,80  e y_m = 1,45.

Imposto quindi una base di 30 cm, e siccome l'altezza minima è 47,39 cm, la trave sarà

30 cm x 50 cm.

 

 

 

SOLAIO IN ACCIAIO

 

Pavimento                  0,4  KN/mq

Massetto                    19   KN/mc

Isolante                      0,2  KN/mc

Cls + lamiera grecata   21  KN/mc

IPE 200                     78,5 KN/mc

 

Carico Strutturale

Cls + lamiera grecata   1,86 KN/mq

IPE 200                      0,45 KN/mq

q_s = 1,86 KN/mq + 0,45 KN/mq = 2,31 KN/mq

Carico Permanente

Massetto                  0,76  KN/mq

Pavimento                0,4    KN/mq

Isolante                   0,012 KN/mq

Impianti + Tramezzi   1,5   KN/mq

q_p = 0,76 KN/mq + 0,4 KN/mq + 0,012 KN/mq + 1,5 KN/mq = 2,672 KN/mq

Carico Accidentale

Ipotizziamo un uso residenziale quindi

q_a = 2 KN/mq

 

Inseriti questi dati nel foglio Excel, scelgo un acciaio S235 che ha f_y,k = 235 N/mm².

Siccome W_{x, min} = 805,14 cm³, scelgo una IPE 360 con W_x = 903,60 cm³.

 

 

 

SOLAIO IN C.A.

Pavimento                  0,4  KN/mq

Massetto                    19   KN/mc

Isolante                      0,2  KN/mc

Getto in cls                 24  KN/mc

Pignatta                      0,91 KN/mc

Intonaco                     18 KN/mc

 

Carico Strutturale

Getto in cls          1,73 KN/mq

Pignatta               0,73 KN/mq

q_s = 1,73 KN/mq + 0,73 KN/mq = 2,46 KN/mq

Carico Permanente

Massetto                  0,76  KN/mq

Pavimento                0,4    KN/mq

Isolante                   0,012 KN/mq

Intonaco                   0,18  KN/mq

Impianti + Tramezzi   1,5   KN/mq

q_p = 0,76 KN/mq + 0,4 KN/mq + 0,012 KN/mq + 0,18 KN/mq + 1,5 KN/mq = 2,852 KN/mq

Carico Accidentale

Ipotizziamo un uso residenziale quindi

q_a = 2 KN/mq

 

Inseriti questi dati nel foglio Excel, scelgo una base di 20 cm e, siccome l'altezza minima

viene di 39,76 cm, scelgo un'altezza di 45 cm. Il sistema, aggiungendo il peso proprio della

trave, calcola un'altezza minima di 40,95 cm e quindi la trave 20 cm x 45 cm risulta

verificata. 

 

 

 

 

La seconda esercitazione prevedeva la realizzazione su sap di una travatura reticolare in 3d e poi il dimensionamento di essa.

La travatura reticolare è stata fatta  con l’obbiettivo di impiegare strutture sempre più leggere per superare luci sempre più grandi.

 

A  questo punto inizio a lavorare sul foglio excel.

Questo file ha alcuni valori che non sono importanti al fine del dimensionamento così inizio a cancellare i dati che non mi servono.

Lascio solo i valori relativi allo sforzo normale e quelli relativi alla lunghezza delle aste.

Posso procedere ad un'ulteriore pulizia, ordinando in modo crescente la luce delle aste cancello tutte le luci diverse da 2 m (che è la luce delle aste normali) e  da 2,82843 m (che corrisponde alla luce delle diagonali   l*radice di 2).

Quindi ho 2 lunghezze di aste

L= 2m

L=2,82843

Ordinando lo sforzo normale posso distinguere quelle a trazioni, da quelle a compressione e le vado a inserire in un altro file excel per fare il dimensionamento.

TRAZIONE:

Inserisco i valori di N positivi dal più piccolo al più grande   nel file excel  per il dimensionamento.

Scelgo  f_yk (coefficiente caratteristico di snervamento) pari a 235 Mpa  e y_m (coefficiente di sicurezza) pari a 1,05.

Il foglio excel ci calcola  la tensione di progetto f_d e l'area minima A_{_min ,} che poi andrà ingegnerizzata.

Devo ora cercare nei profili standard un valore dell'area maggiore dell'area minima calcolata con excel.

 

Questa operazione andrebbe ripetuta per ogni asta.

Nel mio caso ho ordinato le aste secondo l'area minima e le ho divise in 5 gruppi , in questo modo ho utilizzato 5 tipi di profilati diversi.

Riporto qui sotto le aste maggiormente sollecitate per ogni gruppo e il relativo profilo utilizzato.

Compressione:

Inserisco i valori negativi di N

Do un valore a  f_yk (coefficiente caratteristico di snervamento) pari a 235 Mpa e a  y_m (coefficiente di sicurezza) pari a 1,05.

​Il file calcola , oltre alla tensione di progetto f_d e l'area minima A_{_min} , anche I_{_min}  e rho_min . Dovrò dunque ingegnerizzare tutti e tre i valori, individuandolo nella tabella dei profili standard.

Dovrei ripetere l'operazione per ogni asta.

Anche qui ho deciso di dividere le aste in 5 gruppi, stando attenta di mettere nello stesso gruppo quelle con area e caratteristiche simili.

Riporto qui di seguito il dimensionamento dell'asta più solleciatata per ogni gruppo.

 

 

 

 

 

 

 

 La terza esercitazione consiste nel progetto di una trave a sbalzo nelle tre tecnologie di costruzione più comuni (legno, acciaio, cemento armato), con l’ausilio di un foglio elettronico Excel.

Piante di carpenteria di riferimento per solaio in legno,cls e acciaio

La prima carpenteria rappresenta un solaio in cls e legno; la seconda un solaio in acciao.

La trave a sbalzo maggiormente sollecitata è quella sull’asse B, con un’ area di influenza pari a 12 m² (luce: 3m, interasse: 4m).

Lo scopo dell’esercitazione è verificare che la deformabilità della trave non provochi un abbassamento (spostamento verticale) maggiore di 1/250 della luce della trave stessa; il foglio Excel ci permettere di conoscere il valore dello spostamento verticale della trave allo stato limite di esercizio.

Nel caso di una trave a sbalzo, si prende in considerazione il modello statico della mensola

                                           

il cui momento massimo è dato dalla formula  M_max = ql²/2

CEMENTO ARMATO

Considero i valori dei carichi strutturali, permanenti ed accidentali relativi al calcestruzzo della prima esercitazione:

q_s= 3,23 kN/m²

q_p= 2,64 KN/m²

q_a= 2kN/m²  

I tre carichi vengono sommati, moltiplicati per i loro coefficienti di sicurezza e moltiplicati per l’interasse ottenendo q_u pari a 44,64 kN/m. Conoscendo la luce (3 m) , si ottiene il valore del Momento massimo di una mensola  pari a  200,86 KNm.

Per le armature scelgo un acciaio con coefficiente di resistenza caratteristica pari a f_yk=450 MPa e un calcestruzzo con resistenza a compressione pari a f_ck=60 MPa. Imposto una base b pari a 25 cm; i calcoli del foglio Excel mi danno un’altezza minima della sezione che ingegnerizzo a 40 cm. Di conseguenza, ho una sezione di 25 cm X 40 cm.

Dopo aver dimensionato la sezione, effettuo la verifica a deformabilità controllando l’abbassamento massimo dell’elemento strutturale in rapporto alla sua luce.

Il procedimento, che è uguale in tutte e tre le tecnologie, si effettua allo SLE (Stato Limite di Esercizio) poiché la verifica è finalizzata a controllare che non vi siano spostamenti e deformazioni che possano limitare l’uso della costruzione, la sua efficienza e il suo aspetto.

A tal motivo i carichi incidenti sulla struttura vengono ricombinati seguendo la combinazione frequente, generalmente impiegata per gli stati limite di esercizio reversibili:

                                                               q_e= (G1 + G2 + ¥11 × Q1) × i

Nel cemento armato, il peso proprio dell’elemento strutturale veniva calcolato anche nella prima esercitazione, poiché era necessario verificare allo stato limite ultimo (SLU) che la sezione scelta fosse idonea a sopportare tutti i pesi gravanti su di sé anche dopo aver aggiunto il peso proprio. Dopo questa verifica, l’informazione relativa al peso verrà riutilizzata per calcolare il carico totale q_e.

Infine, per calcolare lo spostamento è necessario conoscere il modulo elastico del materiale E e il suo momento d’inerzia I_x

Calcolato il carico totale allo SLE q_e, specificato il modulo elastico E ed il momento di inerzia I_x, è ora possibile calcolare l’abbassamento massimo che è pari a:

                                                                        v_max = q_e* l⁴ / 8EI_x

e verificare che il rapporto tra la luce della trave e il suo spostamento massimo sia maggiore di 250, come imposto dalla normativa in base al tipo di elemento strutturale considerato:

                                                                             l / v_max ≥ 250

Lo spostamento verticale massimo è pari a 1,08 cm e il rapporto tra la luce e lo spostamento massimo è maggiore di 250.

 

LEGNO

q_s= 0,18 kN/m²

q_p= 3,74 KN/m²

q_a= 2kN/m²  

q_u pari a 35,376 kN/m

Conoscendo la luce (3 m) , si ottiene il valore del Momento massimo di una mensola  pari a  159,192 KNm

Dopo aver impostato il modulo elastico del materiale, scelgo una base di lunghezza pari a 25 cm; i calcoli del foglio Excel mi danno un’altezza minima della sezione che ingegnerizzo a 50 cm. Di conseguenza, ho una sezione di 25 cm X 50 cm. Dopo aver dimensionato la sezione, è necessario effettuare la verifica a deformabilità controllando l’abbassamento massimo dell’elemento strutturale in rapporto alla sua luce.

Nel caso del legno, per quanto riguarda il calcolo del carico totale allo stato limite di esercizio, il peso proprio della trave viene trascurato in quanto è un materiale leggero.

                                                          q_e= (G1 + G2 + ¥11 × Q1) × i = 20 kN/m

Calcolato il carico totale allo SLE q_e, specificato il modulo elastico E ed il momento di inerzia I_x, è ora possibile calcolare l’abbassamento massimo che è pari a:

                                                                    v_max = q_e l⁴/ 8EI_x= 0,96 cm.

Di conseguenza:

                                                                             l / v_max> 250

 

ACCIAO

q_s= 1,18 kN/m²

q_p= 1,74 kN/m²

q_a= 2kN/m²

q_u pari a 28,576 kN/m

Conoscendo la luce (3 m) , si ottiene il valore del Momento massimo di una mensola  pari a  128,592 KNm

Dopo aver definito la resistenza del materiale, dal foglio Excel si ottiene un modulo di resistenza a flessione W_x,min pari a 490,99 cm³. Quindi è opportuno utilizzare come profilato una IPE 300 che ha W_x pari a 557,0 cm³ e I_x pari a 8356 cm⁴. 

Dopo aver dimensionato la sezione, è necessario effettuare la verifica a deformabilità controllando l’abbassamento massimo dell’elemento strutturale in rapporto alla sua luce. Come per il cemento, anche per l’acciaio va considerato il peso proprio (0,422 KN/m); informazione che verrà riutilizzata per calcolare il carico totale q_e.

                                                    q_e= (G1 + G2 + ¥11 × Q1) × i = 16,102 kN/m

Calcolato il carico totale allo SLE q_e, specificato il modulo elastico E ed il momento di inerzia I_x, è ora possibile calcolare l’abbassamento massimo che è pari a:

                                                                   v_max = q_e l⁴/ 8EI_x= 0,929 cm.

Di conseguenza:

                                                                              l / v_max> 250