Portale di Meccanica

CENTRO DELLE RIGIDEZZE E RIPARTIZIONE DELLE FORZE SISMICHE (eseguito con Lorenzo Piras)

L’esercitazione guidata è suddivisa in punti, organizzati in ordine cronologico, per eseguire la costruzione e l’analisi un telaio shear type individuandone il centro delle masse, il centro delle rigidezze e il comportamento dello stesso sottoposto a forza sismica.

Vediamo ora come costruire ed analizzare un telaio shear type:

1| Scegliere un telaio composto da travi e pilastri in modo da prenderlo come modello di riferimento (immagine 1).

 1.Modello di telai preso in esame.

 

2|  Lo stesso verrà esaminato in pianta e dopo essere stato quotato adiamo a selezionare quelli che chiameremo da adesso in poi ‘controventi’ o ‘telai’ (ossia,  delle file di pilastri e travi)(immagine 2), andando in fine a disegnare delle ‘molle’, segno che ci ricorda che i nostri telai hanno funzione di assorbire le spinte orizzontali.

2.Quotatura.

 

3| Andiamo ora a riempire con gli opportuni dati richiesti tutta la tabella Excel.

4| E’ possibile calcolare il ‘centro di massa’, il ‘centro delle rigidezze’ e la ‘ripartizioni delle forze sismiche’ (immagine 3).

Dati:

[modulo di young] – 25000

[altezza pilastri] – 3m

[momento di inerzia] – 67500 cm⁴ (inerzia di una sezione quadrata di lato 30cm)

Dato che il nostro telaio è di tipo Shear-Type la struttura orizzontale è infinitamente rigida e quindi indeformabile assialmente mentre i pilastri sono soggetti a flessione. Il telaio perciò subirà, sottoposto a forze orizzontali, solamente spostamenti rigidi orizzontali senza deformarsi,poiché infinitamente rigido. Solamente i pilastri subiranno una deformazione.

[!] si suddivideranno ora i telai nelle tabelle, secondo un ordine da sx a dx dall’alto verso il basso.

3. Compilazione dei dati .

5| Il passaggio successivo è quello di scrivere le distanze ‘orizzontali’ e ‘verticali’ dei singoli controventi rispetto all’origine (immagine 4)

 

4. Compilazione dei dati.

6|Inoltre suddivideremo il nostro impalcato in figure geometriche semplici, per individuarne i centri geometrici degli stessi e del sistema  (‘centro di massa’) (immagine 5)

5.Suddivisione delle aree e individuazione dei centri di massa.

7| Calcoliamo ora le coordinate del ‘centro di rigidezza’, e le distanze di ogni singolo controvento da queste e per trovare le coordinate procederemo allo stesso modo, calcolando a sommatoria del prodotto tra le rigidezze di ogni controvento per le rispettive distanze (verticali o orizzontali in base alla coordinata da trovare) il totale diviso la rigidezza verticale o orizzontale totale.(immagine 6)

Ed infine troviamo la rigidezza torsionale totale dell’impalcato.

 

6. Compilazione dei dati.

8|Scegliere quindi un tipo di pacchetto per un solaio, in modo da definire i carichi permanenti ed accidentali che ci serviranno per proseguire con l’esercizio (immagine 7) ed in automatico si compileranno le ultime due tabelle che ci ripartiscono il carico sismico su tutto l’impalcato.

7. Compilazione dei dati.

9| Come nelle precedenti esercitazioni, analizzeremo il nostro sistema su SAP. Il primo passaggio è quello di ridisegnare l’impalcato, assegnando come vincolo alla base dei pilastri degli incastri (immagine 8).

8. Assegnazione degli incastri.

10| Procediamo adesso con la definizione della sezione dei pilastri in cemento armato, definendo una sezione di dimensioni 30cmx30cm e delle travi di dimensioni 30cmx60cm. (dimensioni bxh)(immagine 9)

9. Definizione delle sezioni di pilastri e travi.

11| Andiamo ora a disegnare il centro di massa e il centro di rigidezza con i dati precedentemente trovati con il calcolo del foglio excell.  (immagine 10).

[!] per disegnare un punto su SAP, basta cliccare sull’icona che raffigura un punto, in alto a sx dello schermo. Si aprirà una piccola finestra dove possiamo inserire le coordinate del punto rispetto all’origine, una volta inseriti i dati cliccare sull’origine del sistema destrorso e chiudere la finestra.

10. Centro di rigidezza e centro di massa.

12| Ora dobbiamo rendere rigida la struttura, quindi andremo a selezionare tutti i nodi (trave/pilastro) ed il centro delle rigidezze. Poi ’Assign’>’Joint’>’Costrains’. Si aprirà una finestra , ‘Assign/Define Costrains’ e a sinistra sul menù a tendina selezionare la voce ‘Diaphragm’. Infine su ‘OK’.(immagine 11).

11. Diaphragm.

13| Dobbiamo rendere indeformabili le travi ( visto che stiamo utilizzando un telaio shear type), per farlo possiamo aumentare il momento di inerzia, andando su ‘Assign’>’Frame’>’Frame Sections’

Si aprirà una finestra, ‘Frame Properties’, selezioniamo la nostra sezione delle travi e quindi su ‘Modify/Show Property’, si aprirà un’altra finestra, ‘I/Wide Flange Section’. Cliccare su ‘Set Modifiers’.

Nell’ultima finestra che si apre, ‘Frame Property/Stiffess Modification Factors’, andiamo ad aumentare la voce ‘Moment of Inertia about 2 axis’ e la voce 'Moment of Inertia about 3 axis'. Infine su ‘OK’. (immagine 12).

12. Aumento del momento di Inerziadelle travi.

 

14| Possiamo adesso assegnare una forza applicata al centro delle rigidezze, in direzione Y pari alla ‘Forza Sismica Orizzontale’ trovata in precedenza con il foglio excel (immagine 13)

13.Assegnazione della forza sismica.

15| Possiamo ora avviare il tasto ‘Run’ e notiamo come il telaio trasli solamente senza ruotare (immagine 14).

14.Assegnazione della forza sismica.

ESERCITAZIONE 6_ ANALISI DI UN ARCO A TRE CERNIERE

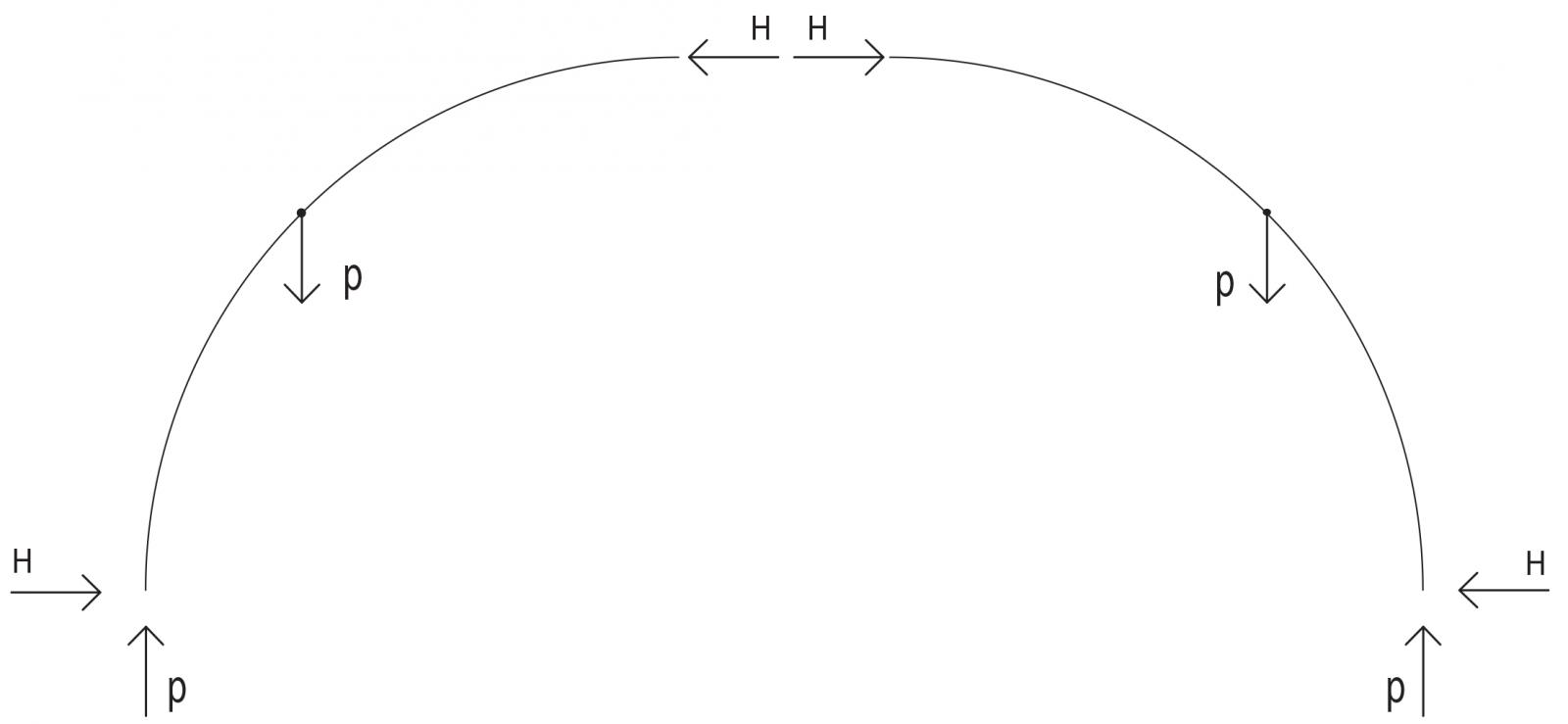
L’arco è una struttura spingente, caratterizzata da una forma particolare che gli permette di avere una ottimizzazione delle sollecitazioni, limitando il momento flettente, trasformandolo in sforzo normale.L’arco a tre cerniere è un sistema isostatico, che è tale per la posizione delle cerniere nello spazio: una nella sezione di chiave, e due nella sezione d’imposta.

 

L’arco è una struttura simmetrica, perciò essendo caricato di una forza pari al suo solo peso proprio, il suo meccanismo sarà il seguente:

Dovendo risolvere un arco sottoposto ad un carico ripartito esterno q, l’equilibrio sarà il seguente:

      

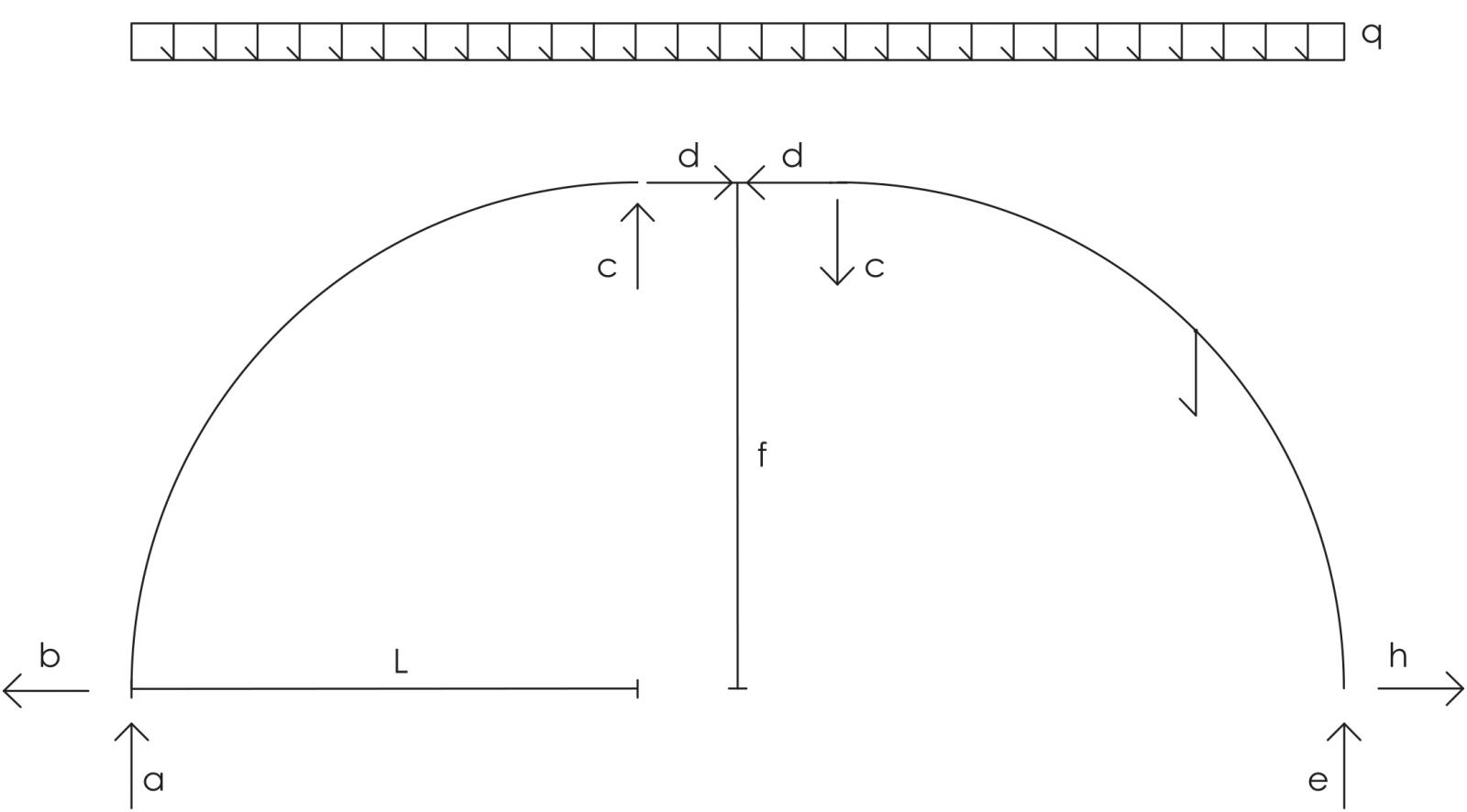
È necessario fare l’equilibrio del 1° corpo intorno ad A:

-ql²/2 – df +cl =0

Momento del 2° corpo intorno a C:

ql²/2 + df +cl =0

Mettendo le due equazioni a sistema:   

-ql²/2 – df +cl =0

ql²/2 + df +cl =0

------------------------

             2cl=0 -> c=0

Per la simmetria della struttura, è chiaro che non ci possano essere forze asimmetriche sull’asse stesso della simmetria. A questo punto si può ricavare il valore della spinta:

-ql²/2 – df = 0

H = -ql²/2f

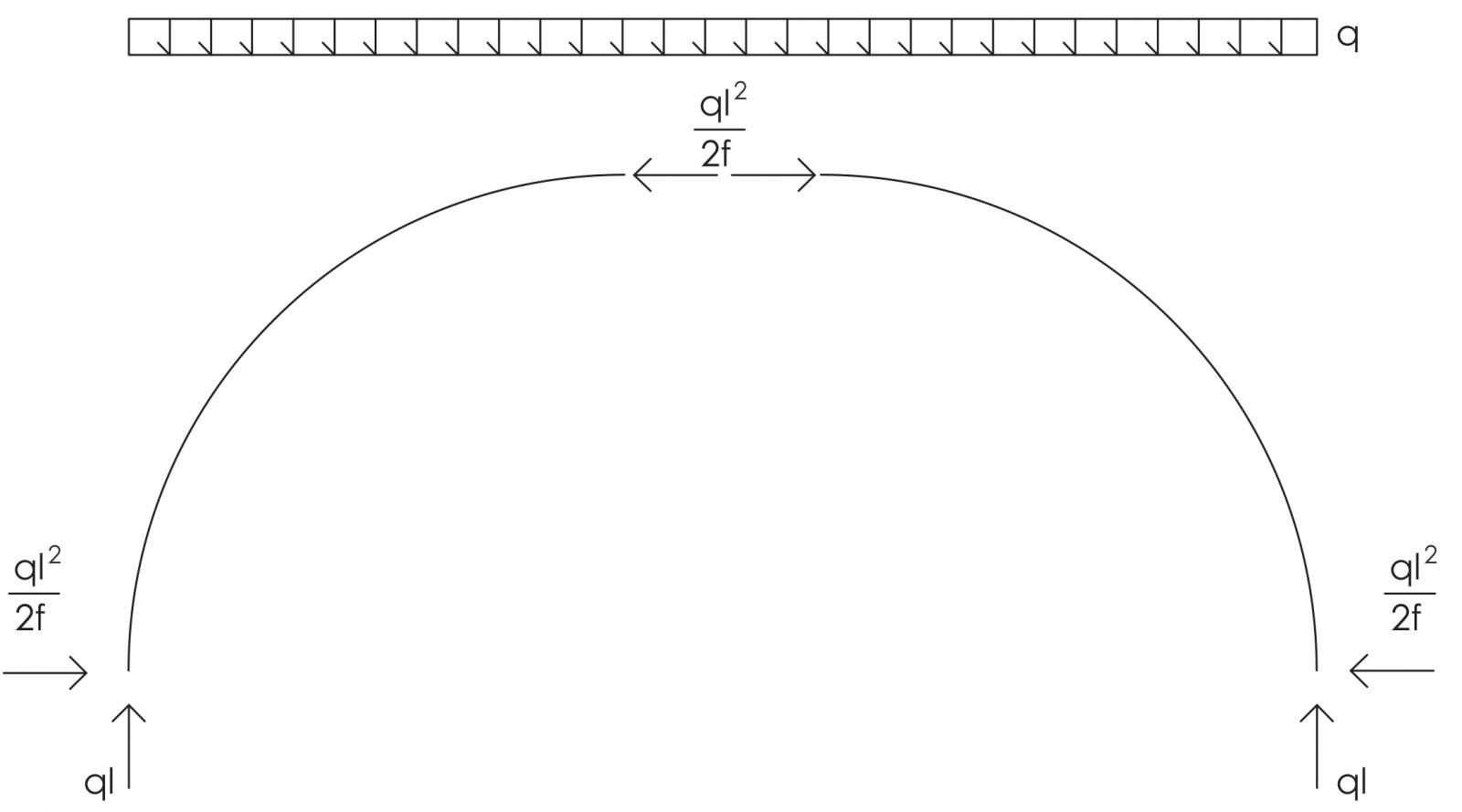
Dalla formula della spinta, si può notare come questa sia inversamente proporzionale alla freccia dell’arco: infatti più questa è di lunghezza inferiore, maggiore è la spinta dell’arco stesso.

È quindi necessario un confronto tra diversi tipi di arco: arco a tutto sesto, arco ribassato, arco parabolico.

1.ANALISI DI ARCO A TUTTO SESTO

 

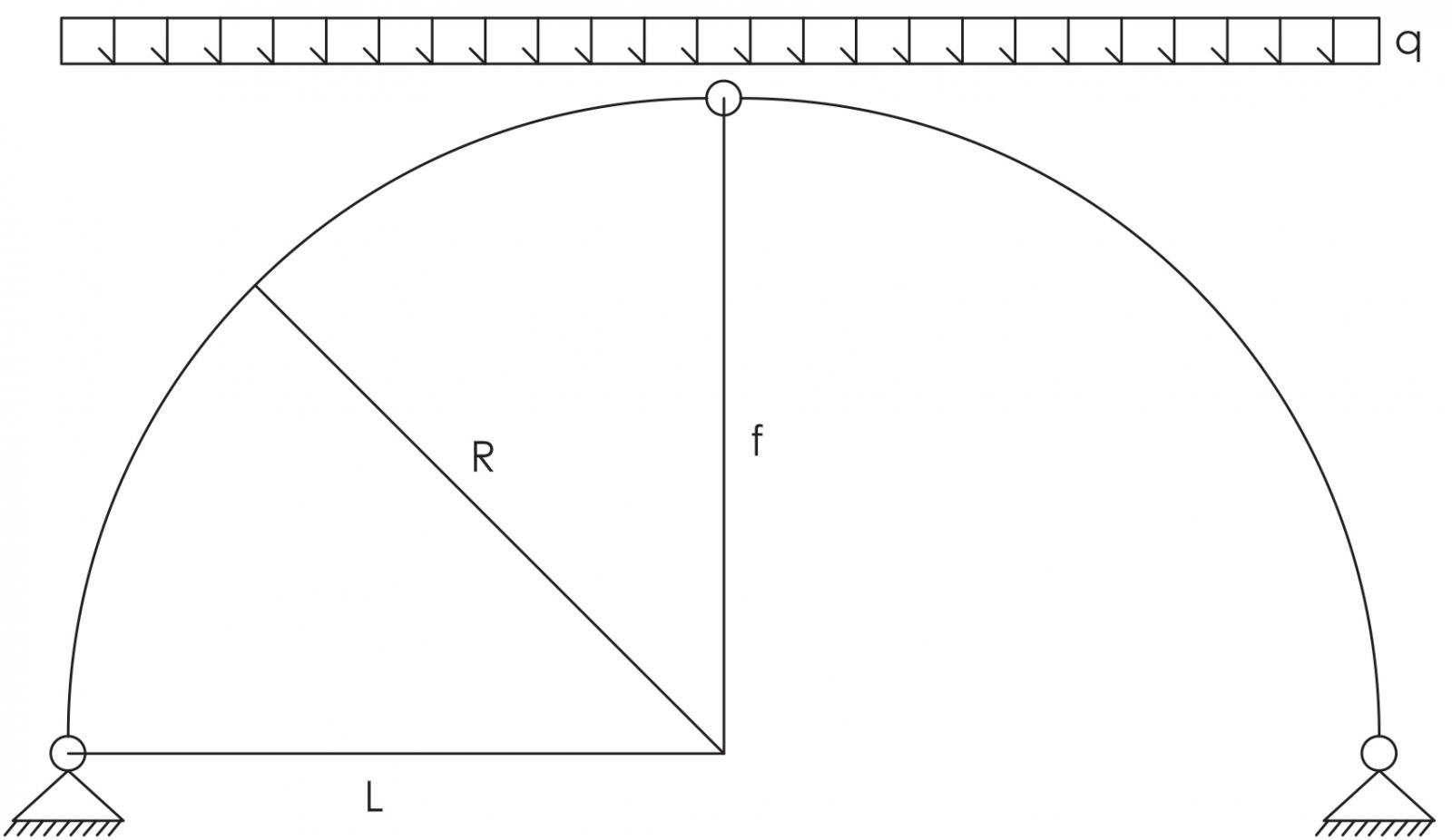
Arco caratterizzato geometricamente dalla coincidenza delle lunghezze del raggio, della freccia, e della luce.

L = R = F

Le sollecitazioni che avvengono nell’arco si verificano in una sezione che la la stessa direzione del raggio. In questo caso, le sollecitazioni vengono espresse non più con coordinate lineari, ma angolari (α è l’angolo al centro). N, T, M sono espresse in funzione di alfa:

-N è perpendicolare alla sezione;

- T è parallelo alla sezione;

- N e T hanno componenti sia orizzontali che verticali, che servono per le equazioni di equilibrio;

- il carico distribuito q, agisce solo sulla proiezione della parte della circonferenza che viene considerata

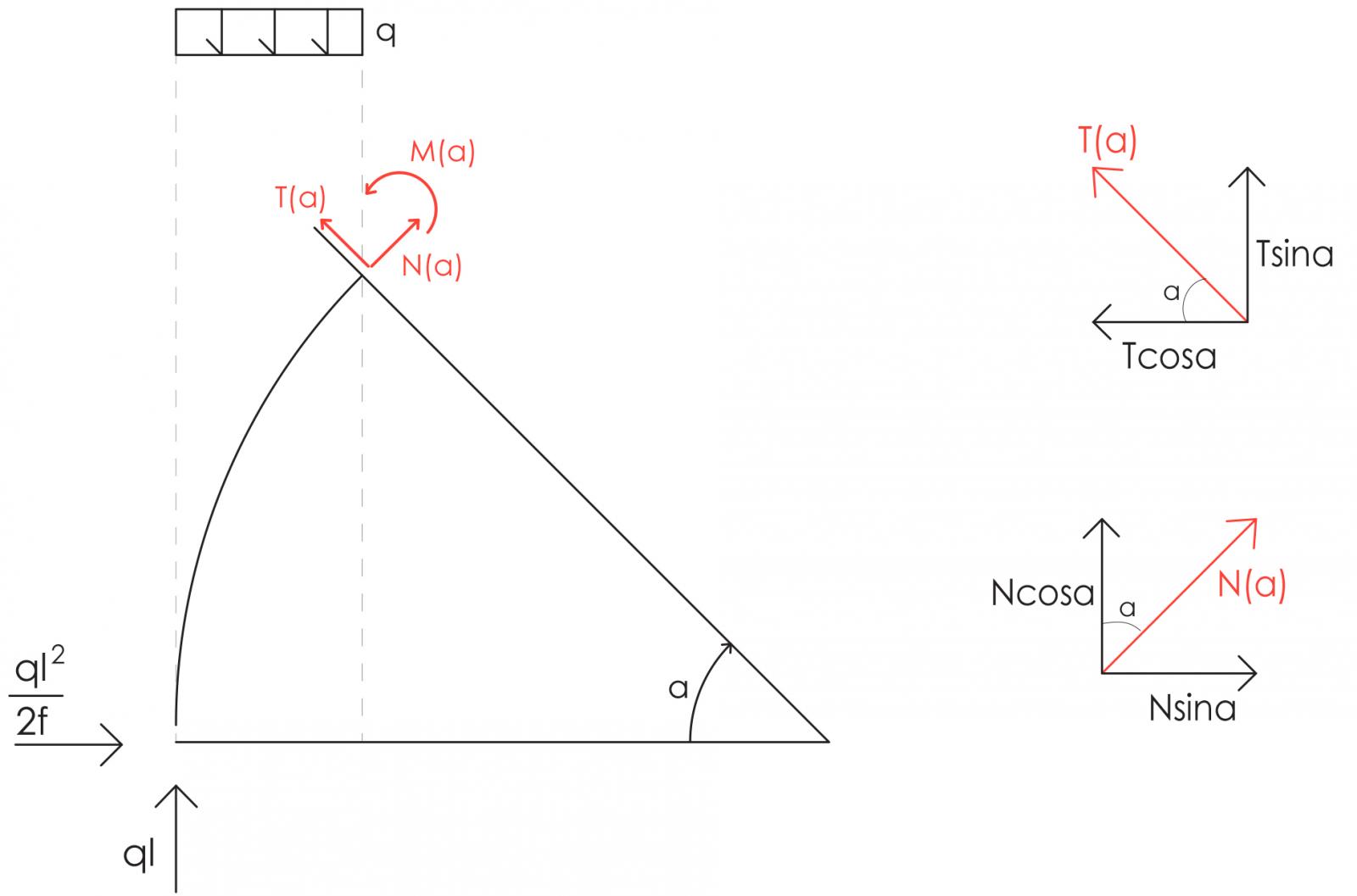
Equilibrio a traslazione orizzontale:

ql²/2f +Nsena – Tcosa =0

Equilibrio a traslazione verticale:

ql + Ncosa + Tsena – qR (1- cosa) =0

Equilibrio dei momenti:

ql²/2f * Rsenα – ql * R(1-cosa) + [qR²(1- cosa)²]/2 – qR²/2 * sena + M(a) = 0

Sapendo che f = L = R:

M(a) = qR² (1- cosa) – [qR²(1- cosa)²]/2 - qR²/2 * sena

M(a) = qR² [(1- cosa) - (1- cosa)²/2 – sena/2]

Questa funzione può essere analizzata in chiave, per avere conferma che la il momento sia nullo.

M (90°) = qR² (1-0) - qR²/2 (1-0)² - qR²/2 *1 =0

M (90°) = qR² - qR²/2 - qR²/2 = 0

Le equazioni di equilibrio orizzontale e verticale vengono messe a sistema, in modo che per sostituzione, si possano ricavare i valori di N e T:

1.qR²/2f +Nsena – Tcosa =0

2.qR + Ncosa + Tsena – qR (1- cosa) =0

 

1.N = Tcosa/sena –qR/2sena

2.qRcosa + Tcosa*cosa/ sena – qRcosa/2sena + Tsena =0

 

1.N = Tcosa/sena –qR/2sena

2.T(cos²a/sena + sena) = qRcosa/2sena -qRcosa

 

1.N = Tcosa/sena –qR/2sena

2.T(1/sena) = qRcosa/2sena –qRcosa -> T= qRcosa*sena/2sena –qRcosa*sena

 

1.N = [qRcosa/2 (1-2sena)]*cosa/sena –qR/2sena

2.T= qRcosa/2 (1-2sena)

 

1.N =  qRcos²a/2sena (1-2sena) –qR/2sena

2.T= qRcosa/2 (1-2sena)

 

1.N =  qR/2sena [cos²a(1-2sena)-1]

2.T= qRcosa/2 (1-2sena)

 

1.N =  -qR/2sena *sena[ sena + 2cos²a]

2.T= qRcosa/2 (1-2sena)

 

1.N =  -qR/2[ sena + 2cos²a]

2.T= qRcosa/2 (1-2sena)

Vengono analizzate queste due equazioni nelle sezioni di imposta e di chiave:

N(0°) = -qR/2 * [0 + 2*1] = -qR = -qL forza entrante nell’arco

T (0°) = qR*1/2 (1-2*0) = qR/2 spinta dell’arco (= qR²/2R)

N(90°) = -qR/2 [ 1 +2* 0 ]= -qR/2  spinta dell’arco entrante nella sezione

T(90°) = qR*0/2(0-2*1) = 0 l’arco è una struttura simmetrica: nella sezione di chiave (asse di simmetria) non possono esserci forze non simmetriche.

Si decide di studiare l’arco anche su SAP. Questo viene disegnato in precedenza su AUTOCAD, ruotato e posto in posizione 3D, e viene salvato in un formato compatibile con SAP (dxf 2004).

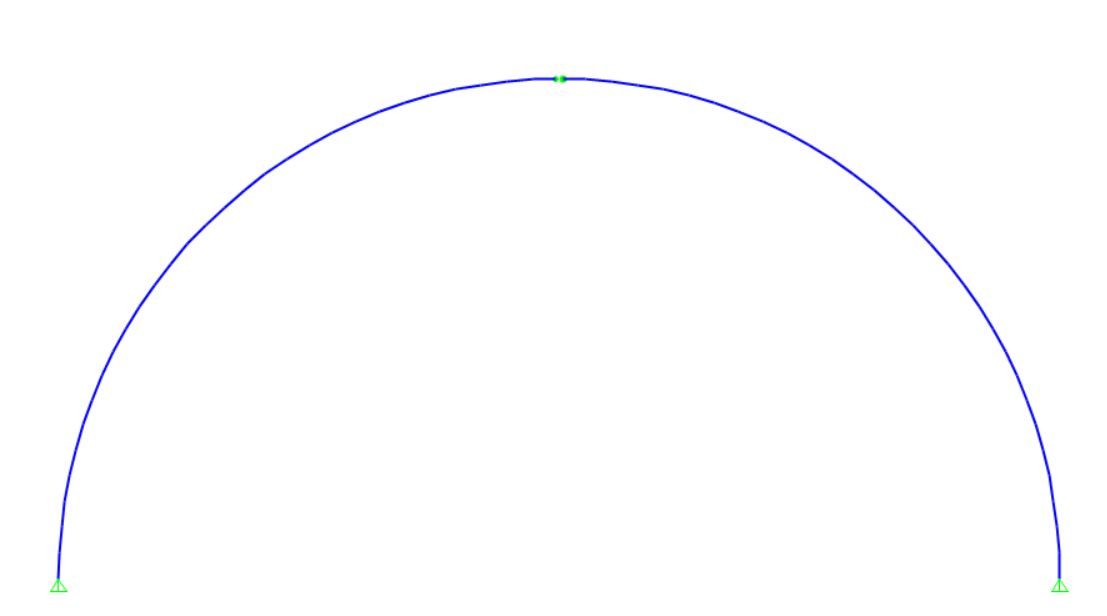
Per determinare il modello di arco a tre cerniere è necessario andare a mettere due cerniere esterne nei punti di imposta, mentre in chiave è necessario selezionare i segmenti della trave, e rilasciare il momento a destra e a sinistra, per creare una cerniera interna.

Successivamente è necessario stabilire la sezione della trave, che nel caso dell’arco è rettangolare e misura 0,3*0,2m.

A questo punto si può selezionare il carico distribuito, che deve essere mandato in maniera uniforme rispetto alla curvatura dell’arco, attraverso il comando “GRAVITY PROJECTED”.

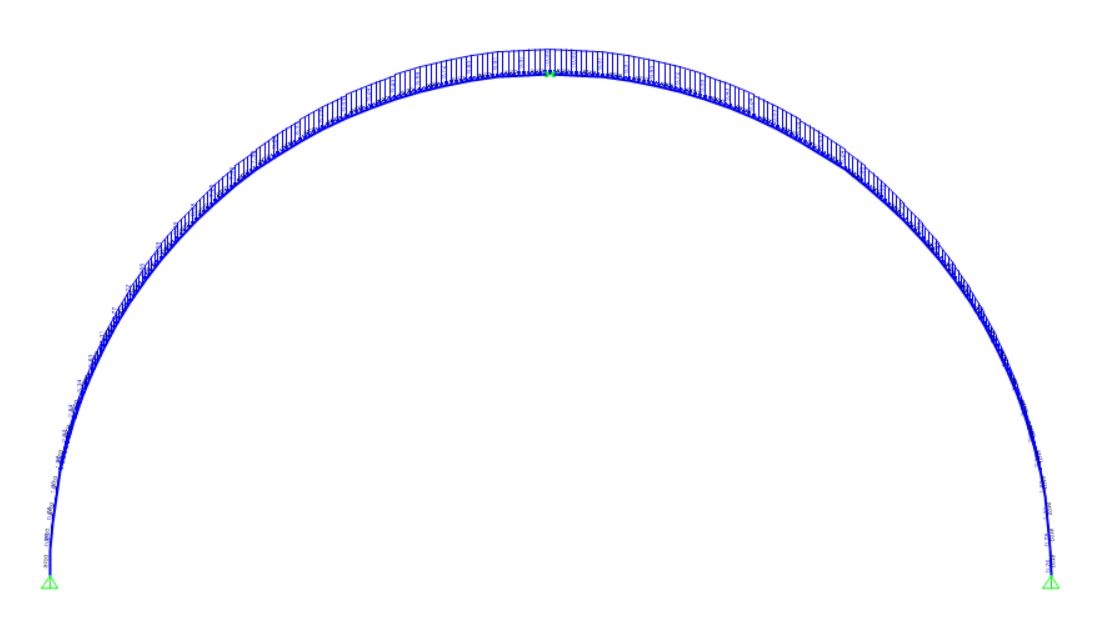
A questo punto è possibile fare l’analisi che da i seguenti risultati:

-le reazioni vincolari sono rispettivamente 30 di forza verticale e 15 di forza orizzontale, in quanto rappresentano uno la reazione vincolare al carico verticale, qR = 10 * 3 = 30 KN e una la spinta orizzontale dell’arco H= qR/2 = 10* 30/2 =15 KN.

-le reazioni risultano essere anche simmetriche rispetto alle due cerniere, in quanto la struttura dell’arco risulta essere completamente simmetrica;

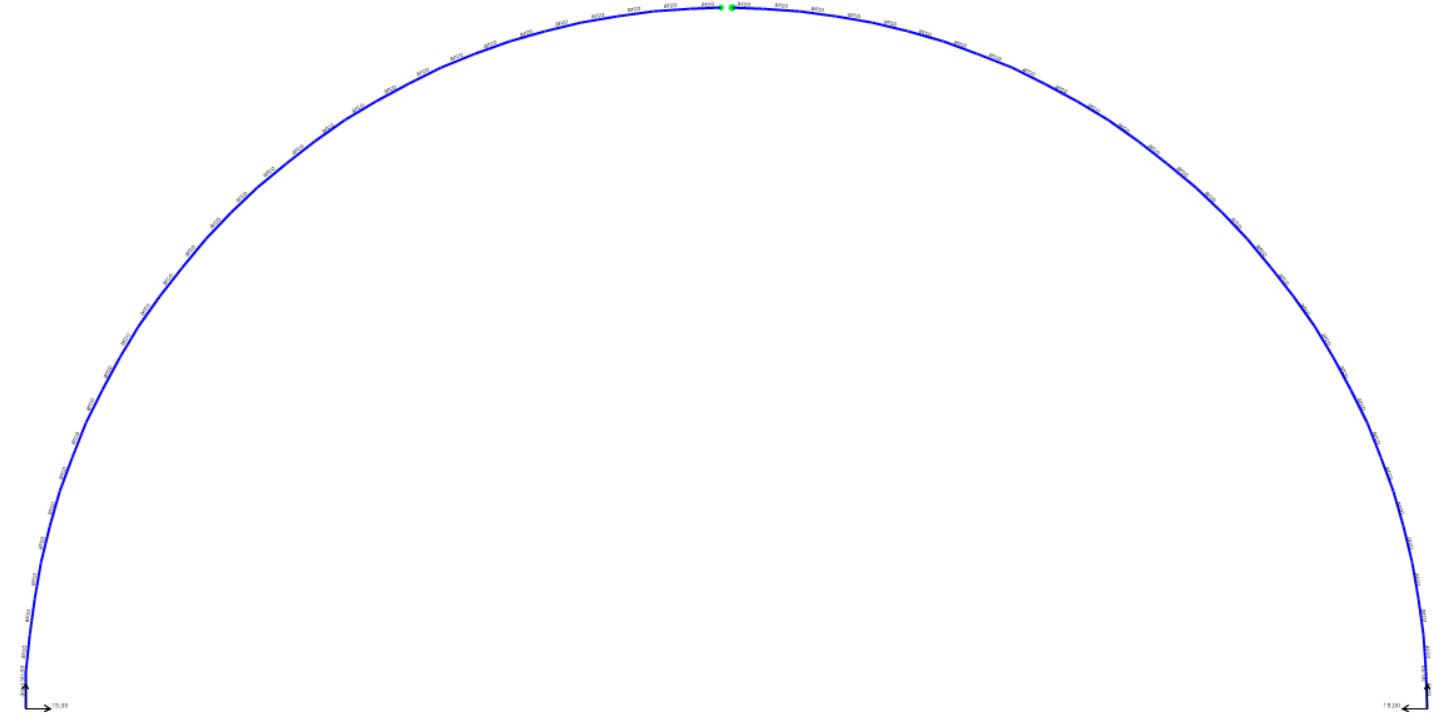
- dal grafico del momento si evince come questo sia nullo sia nelle imposte che in chiave.

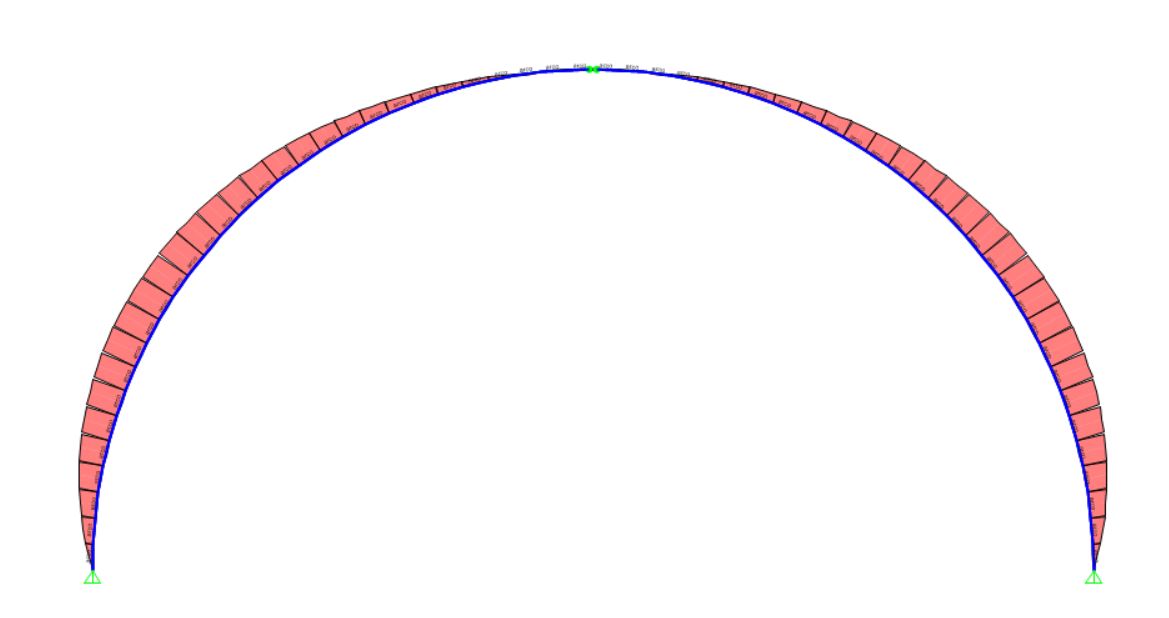
2.ANALISI DI ARCO PARABOLICO

L’arco parabolico è un arco dal comportamento funicolare, ovvero non presenta momento flettente ma solo sforzo normale, una volta in cui viene caricato con un carico uniforme.

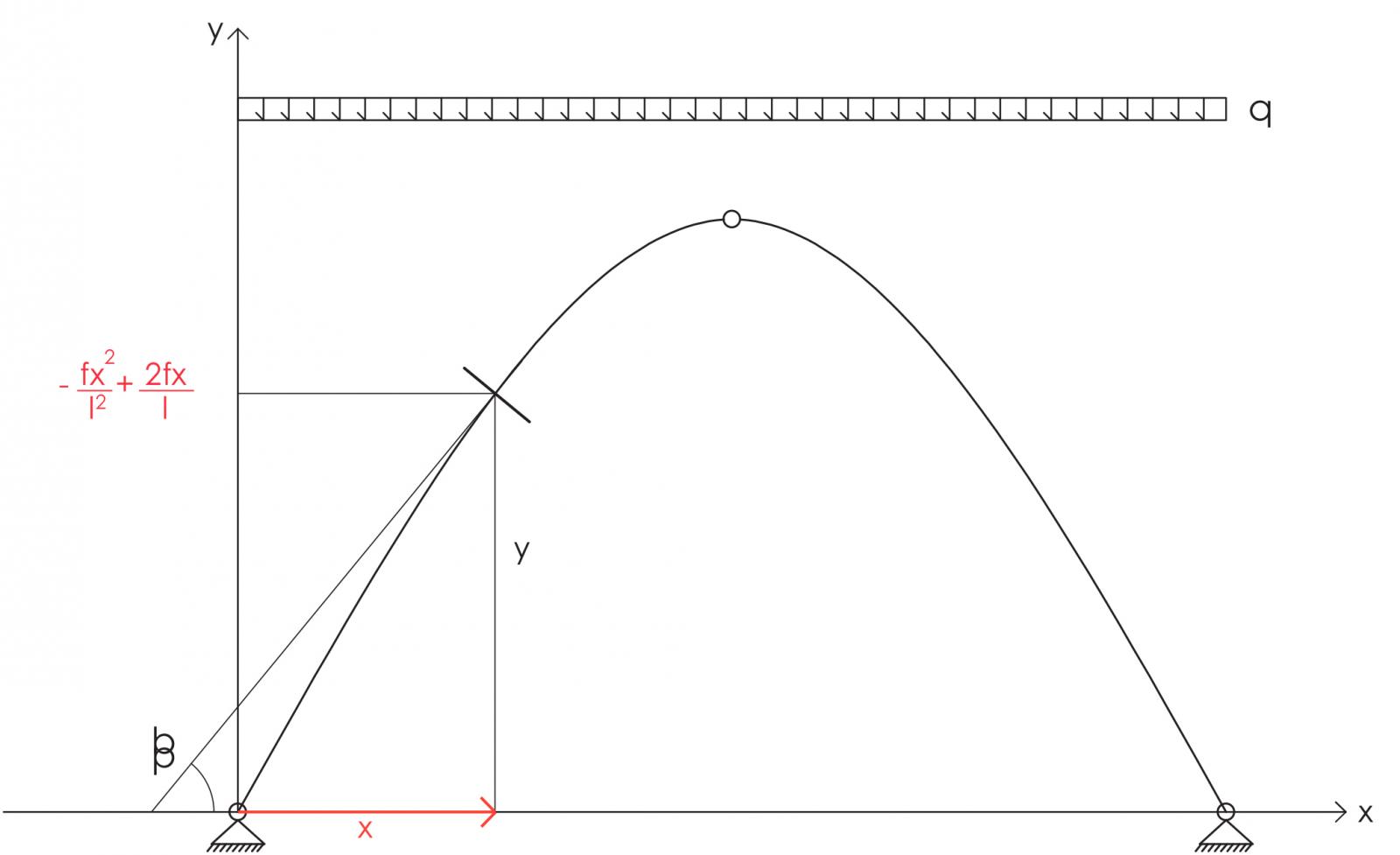
Questo è caratterizzato dalla forma di una parabola, che viene definita da un insieme di coordinate x,y, perciò in questo caso, a differenza che nell’arco a tutto sesto, nell’analisi le coordinate non sono angolari, ma possono essere utilizzate coordinate lineari.

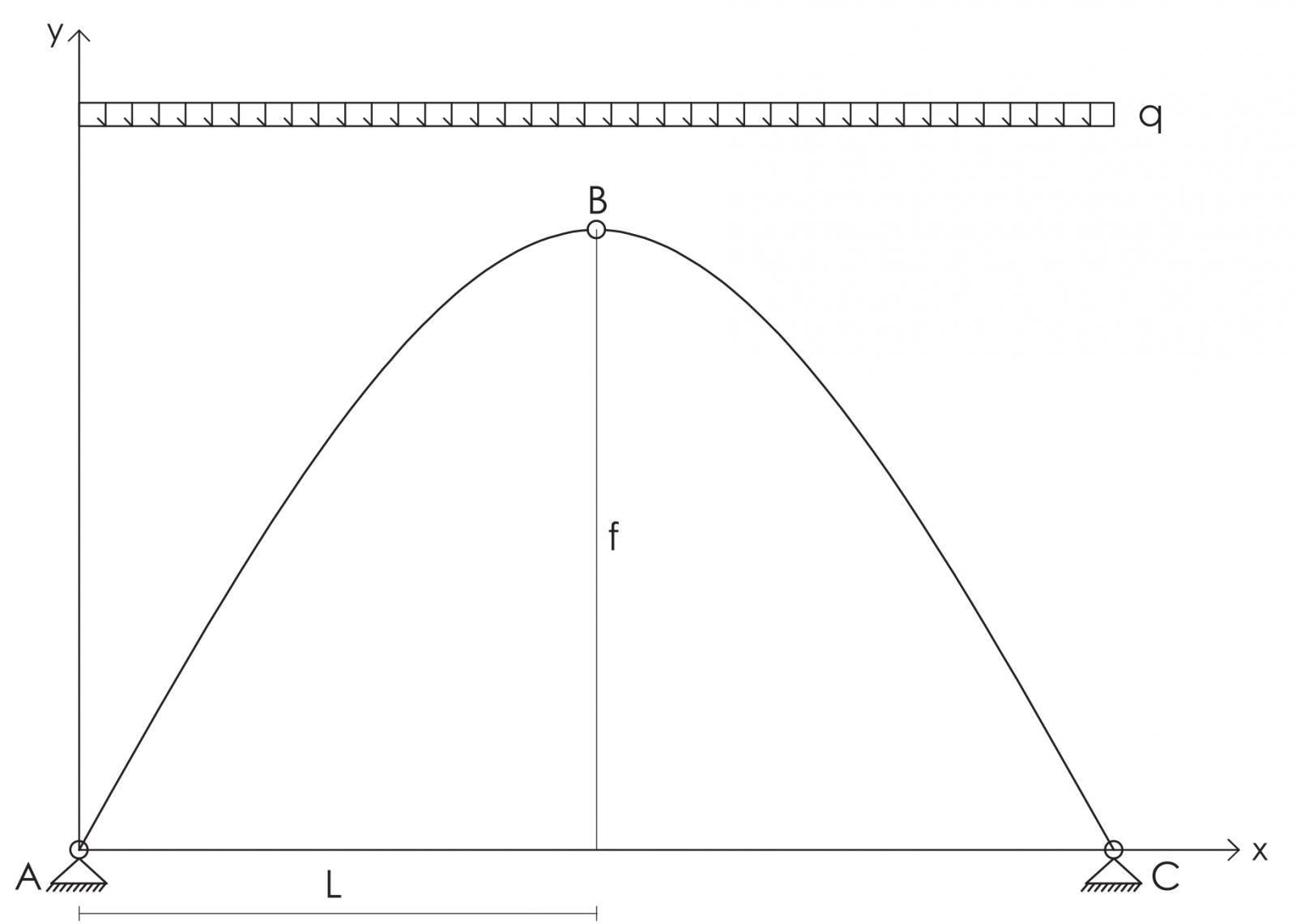
Per analizzare l’arco, è necessario comprendere l’equazione della parabola, quindi sarà necessario capire le coordinate dei punti in cui passa, e da queste, andare a determinare l’equazione:

A (0;0), B (l;f) , C (2l;0)

Sostituendo questi punti all’equazione generica della famiglia di parabole con asse parallelo all’asse y

 (f(x)= y= ax² + bx +c):

f (0;0) ->  0= a*0 + b*0 + c  -> c =0

f(l;f) -> f= al² + bl -> a= -f/l²

f(2l;0) -> 0= 4al² + 2bl -> b= -2al =2f/l

Ne deduciamo che l’equazione è y(x)= -fx²/l² + 2fx/l

Per l’analisi delle sollecitazioni si prende una sezione, tagliando la parabola in un punto (x; -fx²/l² + 2fx/l) e facendo passare per esso una sezione perpendicolare alla curva stessa. La tangente alla curva invece, individua sull’asse x un angolo ß, che è lo stesso che formano N e T all’altezza della sezione, e che serve per ricavare le componenti orizzontali e verticali.

 

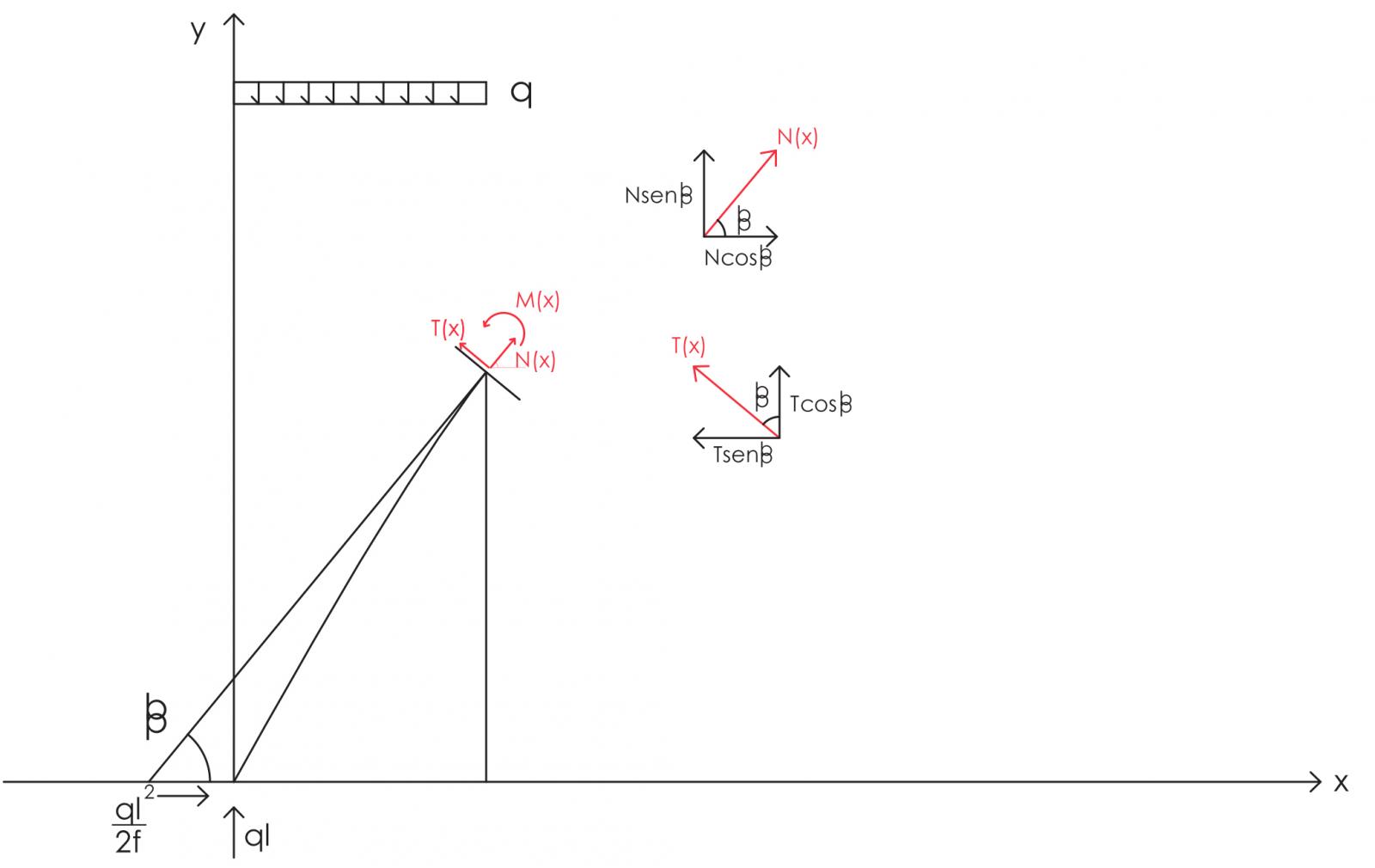
Anche in questo caso si ricorre alle equazioni di equilibrio;

Equazione di equilibrio a traslazione orizzontale:

ql²/2f + Ncosß – Tsinß=0

Equazione di equilibrio a traslazione verticale:

ql – qx + Nsinß + Tcosß=0

Equazione equilibro momenti:

-qlx + ql²/2f * y + qx²/2 + M(x)=0

-qlx - qx²/2 + qlx + qx²/2 + M(x) =0

M(x) =0     il momento è nullo per ogni x della parabola.

Vengono messe a sistema adesso le equazioni di equilibrio a traslazione sia orizzontale che verticale:

1.ql²/2f + Ncosß – Tsinß=0

2.ql – qx + Nsinß + Tcosß=0

 

1.N=TsinB/cosß –ql²/2f cosß -> N=tgß –ql²/2f cosß

2.q(l-x) + (Ttgß –ql²/2f cosß)*sinß + Tcosß=0

 

1.N=tgß –ql²/2f cosß

2.q(l-x) –ql²/2f*tgß +  T tgß*sinß + Tcosß =0

 

1. N=tgß –ql²/2f cosß

2.q(l-x) –ql²/2f*tgß +  T tgß*sinß + Tcosß =0

Sappiamo che tgß= dy/dx = -2fx/l² + 2f/l :

1.N=tgß –ql²/2f cosß

2.q(l-x) –ql²/2f*(-2fx/l² + 2f/l) + Tsin²ß/cosß + Tcosß =0

 

1.N=tgß –ql²/2f cosß

2.q(l-x) + qx – ql + T(sin²ß+cos²ß/cosß) =0

 

1.N=tgß –ql²/2f cosß

2.ql - qx+ qx – ql + T(1/cosß) =0 -> T(1/cosß) =0 -> T=0

Il taglio proprio come il momento è nullo su tutti I punti dell’arco parabolico: l’unica sollecitazione presente è lo sforzo normale, di conseguenza in tutte le sezioni dell’arco, la forza sarà sempre perpendicolare alla sezione stessa.

L’angolo ß dipende dall’ascissa del punto che viene preso sull’arco parabolico e cambia in conseguenza ad esso: nella sezione di imposta ß=0 -> cosß =1

N(0°)=-ql²/2f SPINTA DELL’ARCO.

 

Anche questa volta su SAP viene importato un file in formato dxf, di una parabola dotata di l= 3m e f= 2,425 m.

Questo viene dotato dei vincoli di cerniere esterne e interna come in precedenza.

Successivamente viene dotato di una sezione uguale a quella assegnata per l’arco a tutto sesto 0,3*0,2 m e viene caricato con un carico uniforme secondo la curvatura pari a 10 kN/m.

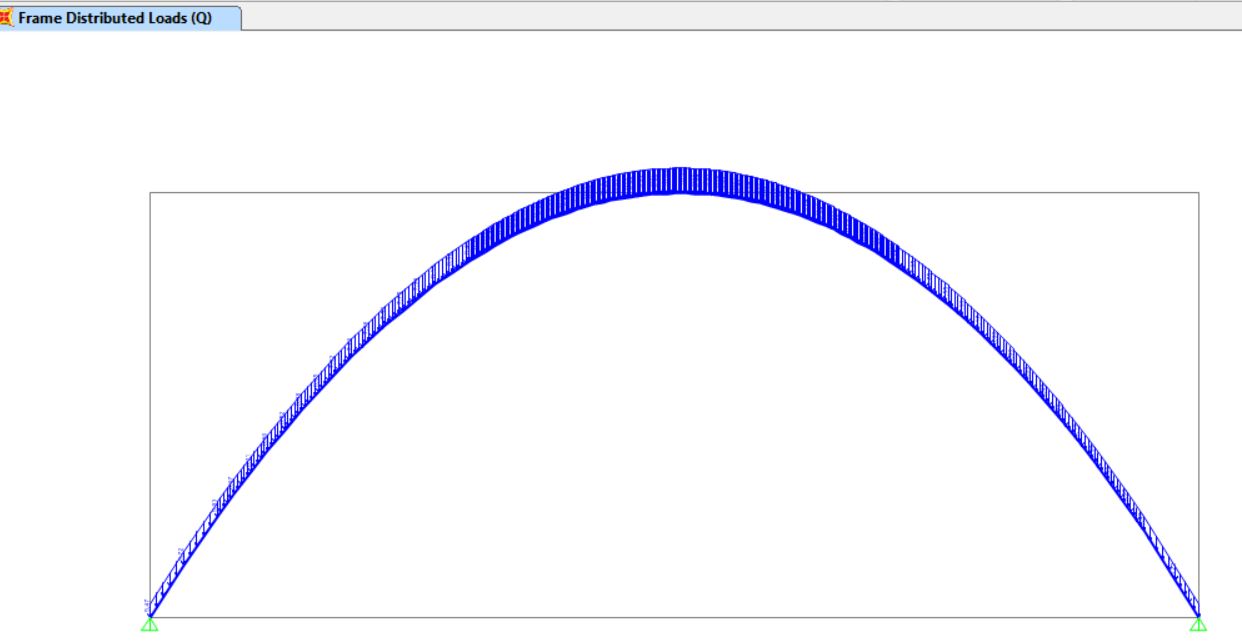
Infine dall’analisi effettuata si possono stabilire delle conclusioni:

-le reazioni vincolari ancora una volta sono congruenti in base ai dati di partenza con le formule precedentemente enunciate

Reazione verticale: ql = 10* 3 = 30 kN

Reazione orizzontale ql²/2f = 10* 9/ 2*2,425 = 18,55 kN

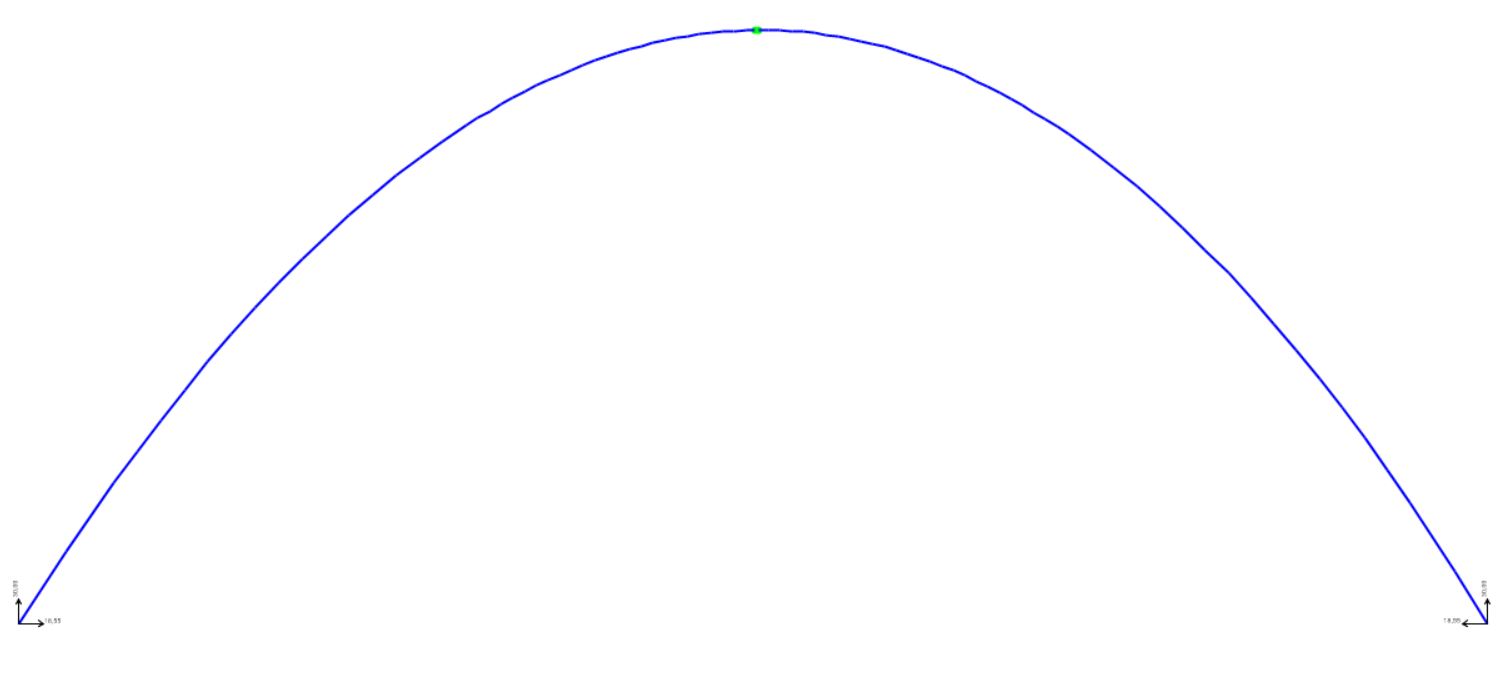
-Essendo questo arco parabolico, dotato di una freccia minore rispetto all’arco a tutto sesto precedentemente analizzato, è possibile osservare come il valore della spinta dell’arco aumenta, in quanto è inversamente proporzionale alla freccia.

Per risolvere una struttura ad arco con SAP dobbiamo utilizzare un programma come autocad o rhino poiché su SAP è impossibile disegnare linee curve (il programma infatti riconosce l’arco come un insieme di punti).

1. ARCO A TUTTO SESTO

Una volta disegnato l’arco su autocad e ruotato con autocad 3d lo importiamo in SAP (salvato in .dxf) 

L'arco è semi circolare (di raggio 6m), la freccia è di 3 m.

 

Per prima cosa mettiamo i vincoli di appoggio agli estremi (assign-joint-restrains) 

 

Dopodichè bisogna inserire una cerniera interna al concio di chiave

Assegniamo quindi la sezione all’arco (cemento 0,4x0,3)

A questo punto assegniamo un carico distributo da 10 kN (assign-frame loads-distribuited) , in direzione gravity projected (cosi il carico è distribuito lungo la lunghezza dei 6m della proiezione a terra dell'arco e non della sua effettiva lunghezza)

Avviamo quindi l'analisi

Le reazioni vincolari  sono verificate:

- reazione vincolare al carico verticale --> qR = 10 x 3 =30 kN 

-spinta orizzontale dell’arco --> qR/2 = 10 x 30/2 15 kN

2. ARCO RIBASSATO

A questo punto importiamo da CAD l'arco ribassato, di luce 3m 

  

Come sopra assegnamo la sezione, i carichi (due cerniera alle imposte e togliamo il momento al conchio di chiave , per simulare una cerniera interna) e mettiamo un carico distribuito , sempre di 10 kN.

A questo punto avviamo l'analisi

Reazioni vincolari:

- reazione vincolare al carico verticale --> qL= 10 x 3 =30 kN 

-spinta orizzontale dell'arco --> qL^2/2F = 10 x 9 / 2 x 2,05 = 21 kN

 

 

 

Esercitazione 5_Studio ripartizioni di forze sismiche in struttura controventata da telai

Scopo di questa esercitazione è quello di analizzare la ripartizione delle forze sismiche in una struttura di un edificio ad un piano. Le forze sismiche sono forze orizzontali e per far fronte a questo, è necessario dotar l’edificio di controventi; il telaio rappresenta un controvento “naturale”, adatto a far fronte a forze orizzontali.                         In questo caso si è scelto di dotare l’edificio di telai shear-type: questi sono un modello idealizzato, dotato di una trave molto resistente, che ha il compito di assorbire la grande parte del taglio e del momento.

 

Per svolgere l’analisi della struttura, è necessario delineare dei telai, sia in orizzontale che in verticale: in base a questo, è possibile andare ad analizzare le rigidezze del telaio, in quanto la rigidezza del telaio è la somma delle rigidezze dei pilastri che ne fanno parte.

Trattandosi di un telaio shear-type, la rigidezza del singolo pilastro è pari a 12EJ/l³ ; tuttavia, andando a considerare telai di più pilastri, la rigidezza sarà 12E/l³ *(J₁ + J₂ +…J_i).

È anche necessario notare come, a livello di pianta, i pilastri, essendo rettangolari saranno regolati in base a come sono tessuti i telai, per essere dotati di maggior momento d’inerzia (in pilastri rettangolari bh³/12) nella direzione utile al telaio; avendo scelto pilastri di sezione rettangolare 0,5*0,3, in cemento armato.

Una volta individuati i telai, questi vengono rappresentati con delle molle, che rappresentano la rigidezza del telaio nel piano dell’impalcato: questo simbolo rappresenta la natura intrinseca nel vincolo, che è un vincolo elastico: con questo si intende la capacità che ha di deformarsi sotto sforzo, e poi di tornare alla sua posizione una volta terminata la spinta della forza esterna.

Grazie lo strumento di excel, è possibile calcolare in modo veloce la ripartizione delle forze sismiche attraverso vari step: il primo è stato quello di inserire nelle tabelle i valori dei parametri per il calcolo delle rigidezze dei diversi telai; i parametri sono i seguenti:

-E (modulo di elasticità) = per la classe di calcestruzzo armato scelta C25/30 il valore del modulo di Young è 31500 MPa (N/mm²);

-J (momento di inezia) = bh³/12, calcolato in base all’orientamento dei telai: per i telai verticali J_x, per quelli orizzontali J_y;

-H (altezza dei pilastri) = molto influente nel calcolo perché viene inserita con l’esponente alla 3.

Vengono così calcolati direttamente i valori delle rigidezze dei telai che formano la struttura.

Sono poi riassunti nel secondo step tutte le rigidezze dei vari controventi, riportate insieme alle rispettive distanze dal punto di origine O, preso coincidente con il pilastro 1. Le distanze dei vari controventi serviranno per calcolare le coordinate del centro delle rigidezze.

Prima del calcolo del centro di rigidezze, che è il punto dove si concentrano idealmente le forze reattive di tutti i controventi, è necessario andare a trovare il centro di massa, o baricentro, che è invece il punto dove idealmente si concentrano tutte le forze esterne, che spingono il corpo a trasformarsi.

Per calcolare il centro di massa è necessario scomporre l’area totale in delle aree semplificate, andando a trovare i baricentri delle singole, per poi risalire a quello dell’intera struttura.

X_G=15,78 ; Y_G= 5,22

Una volta calcolato il baricentro, si può passare al calcolo del centro delle rigidezze: le coordinate vengono ottenute attraverso le seguenti formule:

X_c= K*/Ko_tot  ;   Y_c= K* / Kv_tot

Dove K*(momento risultante delle rigidezze)= k₁*d₁ + k₂*d₂ + k₃* d_{3 …}+k_i*d_i

Successivamente viene calcolata la rigidezza torzionale totale, grazie alla formula: ∑k_oi* d_oi² +∑ k_vi* d_vi²

Per l’analisi delle forze sismiche è necessario calcolare la risultante di queste forze: questa viene calcolata basandosi sui carichi sia di natura permanente G, sia di natura accidentale Q, che vengono moltiplicati per l’area dell’impalcato su cui agiscono; questi poi vengono moltiplicati per un coefficiente sismico, il coefficiente di contemporaneità Ψ (=0,80) ottenendo il fattore W(pesi sismici) il quale, moltiplicato per un altro coefficiente c (=0,10), di intensità sismica, dà il valore della forza sismica orizzontale F (KN).

Infine tramite il foglio excel è possibile anche osservare la ripartizione delle forze sismiche orizzontali lungo x e lungo y (F_x; F_y):i pilastri non effettuano traslazioni sulla base, in quanto questi sono incastrati, ma traslano nell’estremità opposta, ottenendo al contempo un momento torcente. Questo dipende dalla forza sismica orizzontale che viene moltiplicata per la differenza delle coordinate delle ordinate del centro di rigidezze – il centro di massa: M_x= F(Y_C-Y_G).

La traslazione lungo l’asse x (u_o) si ottiene dalla formula F= k*δ, dove δ= u_o= F/k_o_tot.

Un altro valore importante è la rotazione dell’impalcato, generata dal rapporto del momento torcente e della rigidezza torsionale totale. Φ= M_x/ K_tot.

Infine vengono poi indicate per ogni controvento, le forze che vi agiscono, queste sono ottenute dal prodotto della rigidezza del controvento, della sua distanza dall’origine e infine della rotazione dell’impalcato.

Lo stesso viene ottenuto anche per le forze sismiche che agiscono lungo l’asse y.

Si ricrea lo stesso modello su SAP, per verificare i risultati ottenuti: trattandosi di un impalcato infinitamente rigido ci si aspetta una semplice traslazione di tutto l’impalcato, ottenuta dalla deformazione dei pilastri ad “S”, secondo il modello sher-type, con il punto di nullo del momento a ½ dell’altezza.

-si ridisegna la struttura;

-vengono incastrati i pilastri a terra, secondo il modello shear-type;

-vengono definite le sezioni degli elementi: i pilastri 1-2-3-4-5-6 vengono dotati di una sezione di 0,5*0,3m, i pilastri 7-8-9-10 vengono dotati di una sezione di 0,3*0,5m, mentre le travi vengono realizzate di sezione 0,4*1,0m. Inoltre, sono state modificati i moduli di elasticità dei pilastri, per renderli conformi a il dato utilizzato in excel (31500 N/mmq), sia è stato cresciuto esponenzialmente il modulo E delle travi, per renderle infinitamente rigide, cercando di raggiungere il più possibile il modello ideale di shear-type.

-è poi necessario inserire il centro delle rigidezze, utilizzando le coordinate ottenute su excel:

X_c= 18,79  Y_c= 3,74

-si assegna un vincolo interno (diaphragm) in modo da rendere l’impalcato rigido;

-si assegna la forza sismica ottenuta su excel (F=170,64 KN), facendola agire sul centro delle rigidezze della struttura.

-si effettua l’analisi e si osservano i risultati:

come previsto, la deformata mostra una traslazione rigida dell’impalcato (la rotazione è praticamente irrisoria) e la deformazione dei pilastri avviene tramite la forma ad S;

-il grafico del momento mostra come questo nei pilastri sia lineare, e praticamente come si annulli, tralasciando piccolissimi errori decimali ad ½ dell’altezza dei pilastri;

 

Struttura in pianta:

Per lo sviluppo di questa esercitazione ho ripreso gli stessi pacchetti di solaio utilizzati per l'esercitazione precedente. Andrò a prendere in esame la trave centrale poiché quella più sottoposta a sollecitazione. L'area di influenza è evidenziata con il tratteggio. Nel file excel vado poi ad inserire i valori già precedentemente calcolati (nell'esercitazione 2) per i carichi per andare ad effetture la verica di abbassamento. Sappiamo che nel caso di una mensola il momento sarà uguale a M=ql²/2. La verifica che andremo ad effettuare sarà che il rapporto tra sbalzo ed abbassamento massimo sia maggiore o uguale a 250.

Vado a verificare per ogni singolo pacchetto di solaio:

LEGNO:

Nel secondo esempio vedendo che il rapporto non risultava verificato, vado a diminuire la base della trave in modo da avere un'altezza maggiore. Una trave più snella mostra maggiore resistenza a flessione.

ACCIAIO:

CLS:

Aggiunti i 5 cm di copriferro all'altezza della trave, normalizzo in base all'altezza di Design, e vado a soddisfare la verifica poiché v/lmax > di 250.

Per sviluppare la terza esercitazione mi sono basata sulla seconda, usando gli stessi pacchetti di solaio per il cls, l’acciaio ed il legno.Per sviluppare la terza esercitazione mi sono basata sulla seconda, usando gli stessi pacchetti di solaio per il cls, l’acciaio ed il legno.

 

Consideriamo la trave centrale, poiché è quella più sollecitata, e la sua area di influenza in azzurro.

Dopodiché inserisco i valori ottenuti dalla precedente esercitazione nel file excel per la verifica ad abbassamento.

Nel caso dalla trave appoggiata avevamo un momento uguale a qL^2/8, mentre ora avremo che M=qL^2/2.

In tutte le tipologie costruttive usate dobbiamo verificare che il rapporto tra lo sbalzo e l’abbassamento massimo deve essere maggiore o uguale a 250.

 

ACCIAIO

 

Basandomi sul modulo di resistenza Wx, decido di usare un’Ipe 330, la sezione della mensola è verificata.

 

LEGNO

La sezione della mensola è verificata.

 

CLS

L/vmax=359,12

La sezione è verificata.

Questa quinta esercitazione vuole mettere in mostra il diverso comportamento di tre strutture ad arco che coprono la stessa luce ( L=10 m; FIG.01), aventi la stessa sezione (30 x 50 cm, FIG 03), di forma diversa sottoposte all'azione di un carico distribuito q= 100kN (FIG.02).

La prima è rappresentata da un arco circolare in cui la fraccia è uguale alla metà della luce: (f=L/2)

La seconda è rappresentata da un arco ribassato in cui la freccia è un quarto della luce (f=L/4)

L'ultima é un arco parabolico in cui la frecca è pari alla lunghezza della luce (f=L)

FIG.01

 

FIG.02

FIG.03

FIG.04

La loro deformata è simile ma le loro reazioni vincolari sono molto diverse. La FIG. 05 mostra come l'arco ribassato rappresenti la struttura più spingete di tutte tanto che la reazione vincolare orizzontale è pari a circa 500 kN, la metà della reazione vincolare dell'aco circolare (250 kN) ed un quarto della reazione vincolare dell'arco parabolico ( 125 kN).

FIG.05

I diagrammi dello sfrozo normale confermano quel che già era stato visto dalle reazioni vincolari e ci permettono di fare ulteriori ragionamenti riguardanti lo sfrozo normale. 

Nell'arco circolare in corrispondeza delle cerniere esterne l'arco arriva a tangente verticale, di conseguenza lo sfrozo normale sarà pari alla reazione vincolare verticale.

Nell'arco ribassato e nell'arco parabolico, lo sforzo normale è inclinato secondo l'asse dell'arco e le sue componenti orizzontali e verticali possono essere rintracciate nelle reazioni vincolari che si generano nella cerniera esterna.

N₁²=(500,44)²+(500)²=> N₁=702,68 kN

N₂²=(125)²+(500)²=> N₂=514,30 kN

 

FIG.06

La quinta esercitazione prevede lo studio di un arco con il software SAP. L’arco rappresenta una tipologia di struttura che lavora a sforzo normale, grazie alla sua geometria, che gli permette di lavorare non per massa, ma per forma riuscendo a superare grandi luci dato che non funziona a flessione ottimizzando anche l’impiego di materiale.

Per il disegno di un arco a tutto sesto si è utilizzato il programma AUTOCAD, grazie al quale è stato possibile realizzare un arco con una luce di 6m.  Una volta realizzato il modello, si è salvato il file in formato DXF e poi lo si è importato direttamente sul programma SAP. 

Dato che il modello di riferimento, in tal caso, è un arco a tre cerniere, si è proceduto con l’assegnare in corrispondenza della linea d’imposta due cerniere esterne: dopo aver selezionato i due punti -> Assign -> Joint -> Cerniera

Per inserire la cerniera in chiave il procedimento prevede di selezionare il segmento precedente e quello successivo al punto che coincide con la chiave dell’arco e poi impostare il comando: Assign -> Release -> spuntare una volta la casella “end” e una volta la casella “start” in corrispondenza del Momento 33 per il rilascio del momento, che deve essere assente.

Successivamente si è assegnata una sezione alla struttura; si è optato per una sezione rettangolare in calcestruzzo pari a 0,3x0,4 m.

L’arco è stato, poi, sottoposto ad un carico uniformemente distribuito ed impostato attraverso i seguenti comandi: si è selezionato l’arco -> Assign -> Frame Loads -> Distributed -> impostare un carico Q trascurando il peso proprio della sezione dell’arco -> in corrispondenza della voce Direction si è impostata la condizione: Gravity Projected per indicare un carico pari a 10 KN/m non distribuito sulla lunghezza dell’arco, ma sulla sua proiezione a terra.

Si è avviata l’analisi e si è visto che il carico totale pari a 10 KN/m x 6m = 60 KN è stato ripartito equamente in corrispondenza dell’imposta; se si considera metà arco qxl = 10 KN/m x 3m (metà luce) = 30 KN pari alla metà del carico totale, mentre in chiave si ha qxl/2 = 10 KN/m x 3m /2 = 15 KN.

ARCO PARABOLICO

Dopo aver rappresentato sul programma SAP un arco a tutto sesto si è proceduto con la realizzazione di un modello di un arco parabolico (di equazione y= ax²+bx+c) con tre cerniere e caricato anche esso con un carico q uniforme. Dai risultati che fornirà il software SAP ci si aspetta che l’arco assuma un comportamento funicolare, per cui momento flettente e taglio sono nulli, mentre tutto il carico viene trasformato in sforzo normale.

Si è disegnato un arco usando il programma AUTOCAD con il comando “Spline” con luce pari a 6 metri, uguale a quella dell’arco a tutto sesto rappresentato precedentemente. Successivamente lo si è salvato in formato DXF ed importato su SAP.

Anche in questo caso sono stati applicati i vincoli cerniera all’imposta dell’arco.

In chiave è stata inserita una cerniera interna seguendo la stessa modalità descritta per l’arco a tutto sesto.

Si è selezionato l’intero arco ed è stata adottata una sezione in calcestruzzo di dimensioni pari a 30 cm x 40 cm.

È stato applicato un carico distribuito pari a 10 KN/m, senza considerare il peso proprio dell’arco, e non distribuito su tutta la lunghezza dell’arco stesso, ma solo sulla sua proiezione a terra.

Si è avviata l’analisi grazie alla quale è stato possibile notare che la reazione vincolare orizzontale, considerando metà arco (per una luce = 3m) risulta essere uguale a quella dell’arco a tutto sesto, ovvero 30KN, che deriva da: 10KN/m x 3m. Per ciò che riguarda la reazione verticale essa non è pari a ql/2, ma deriva da: ql²/2f dove f sta ad indicare la freccia dell’arco che nell’arco parabolico è diversa dalla luce l.

Per questa esercitazione ci viene richiesto di andare a risolvere una struttura ad arco con il software SAP.
Questo tipo di struttura, reagisce grazie alla propria geometria e tende a lavorare solo con sforzo normale, quindi in maniera omogenea su tutta la sezione, avendo così un’ottimizzazione del materiale (nel momento per esempio, le fibre al centro della sezione lavorano meno rispetto quelle esterne).
Data l’impossibilità di utilizzare il programma per disegnare linee curve, utilizzeremo un programma CAD (autoCAD, Rhino, etc.).
Una volta esportato il file (.dxf, .iges) importiamolo sul programma SAP.
Svolgiamo prima il caso dell’arco a tutto sesto, ovvero quando la freccia è pari a metà della luca (semicircolare), dimostrando che tra le reazioni vincolari (appoggiato-appoggiato) risulteranno anche azioni orizzontali, quindi spingenti lateralmente.
Una volta preso metà arco in considerazione (tenendo conto che il concio di chiave è rappresentabile come una cerniera interna), possiamo dimostrare come la reazione verticale sull’appoggio risulterà uguale a metà carico equamente distribuito sulla proiezione dell’arco (quindi q*l, dove l è metà luce), mentre tramite equilibrio dei momenti dimostriamo come la reazione orizzontale sull’appoggio (verso l’interno) risulterà uguale a ql/2.

Importiamo il disegno su SAP.

Mettiamo i vincoli di appoggio agli estremi.

Andiamo ad inserire una cerniera interna sul concio di chiave.

Applichiamo ora una sezione in cemento armato all’intero arco (ottimizzato già con la stessa sezione su tutta la lunghezza).

Andiamo a togliere il peso proprio della struttura e a applicare un carico distribuito q pari a 10 Kn/m sulla proiezione dell’arco a terra, non sulla lunghezza dell’arco (gravity projected).

Calcoliamo ora le reazioni.

I risultati corrispondono a quelli descritti nell’analisi spiegata sopra.

Analizziamo ora il caso di un arco parabolico, ovvero un arco il cui andamento corrisponde all’andamento di una parabola, quindi di equazione y(x)=ax^2+bx+c.

Dopo averlo disegnato tramite SpLine su autoCAD, importiamo il file su SAP.

Applichiamo i vincoli (appoggio - appoggio).

Applichiamo una cerniera interna nel concio di chiave.

Applichiamo la sezione come nel caso precedente,

e anche il carico distribuito sulla proiezione dell’arco.

Calcoliamo le reazioni vincolari.

Notiamo come mentre la reazione verticale rimane la stessa, l’orizzontale ovviamente sarà diversa, dato che in questo caso, non corrisponde allo sforzo normale.  Tale reazione sarà uguale a ql^2/2f (dove f corrisponde alla freccia dell’arco 6m nel nostro caso).

Proviamo ora ad eliminare le azioni spingenti lateralmente tramite l’addizione di due mensole esterne.
Provando a calcolare manualmente le razione di questa situazione, siamo riusciti a trovare che per eliminare totalmente queste spinte le mensole devono avere una lunghezza, in proiezione sull’asse X pari al prodotto della semiluce e la radice quadrata del rapporto tra carico q sull’arco e carico q sulla mensola:

b=l*sqrt(q1/q2)

Immaginando q1=q2, per eliminare lo sforzo orizzontale avrei dovuto inserire mensole di una lunghezza tale da avere una proiezione sull’asse X di 3m.

Ho riscontrato problemi nell’importazione del file cad, ho quindi disegnato direttamente su SAP le mensole inserendo le coordinate dei punti negli estremi.

Applichiamo ora lo stesso carico distribuito anche sulle mensole, sempre sulla proiezione di queste sull’asse X.

Applichiamo la sezione in cemento armato.

Dato che utilizziamo un carico distribuito agente sulla proiezione della struttura sull’asse orizzontale, l’inclinazione della mensola non influirà sulle reazioni vincolari (ovviamente influirà sulle sollecitazioni e  sulle deformazioni), dimostriamolo utilizzando due mensole di differenti inclinazioni ma uguale proiezione.

Il risultato della reazioni verticali sarà la somma tra q1*l e q2*b, mentre quelle orizzontali saranno uguali a 0 come immaginavamo.
In conclusione è quindi possibile eliminare le spinte orizzontali tramite alcune scelte già in fase progettuale.