Portale di Meccanica

Esercitazione realizzata da Rebecca Brock e Francesca Di Gregorio.

Abbiamo scelto un unico telaio per tutte e tre le differenti tecnologie:

 

ACCIAIO:

- Analisi dei carichi:

Qs: carico strutturale

• lamiera grecata + soletta = 1,65 kN/m²
• IPE 140 γ = 12,9 kN/m³, interasse = 2,3 m

Qs = 1,65 + (12,9 x 1/2,3) = 1,704 kN/m² 

Qp: carico permanente

• isolante termico γ = 7,97 kN/m³
• massetto γ = 21 kN/m³ 
• pavimentazione parquet γ = 7,2 kN/m³ 
• impianti 0,5 kN/m
• tramezzi 1 kN/m

Qp = (0,04 x 7,97) + (0,05 x 21) + (0,02 x 7,2) + 0,5 + 1 = 3,0128 kN/m²

Qa: carico accidentale

Qa = 2 kN/m²

- Dimensionamento travi

Su un foglio di calcolo Excel abbiamo inserito i valori trovati e calcolato la combinazione di carico al metro lineare. Poiché la struttura è iperstatica, abbiamo individuato il momento massimo, M_max, come se fosse una trave appoggiata-appoggiata (M=ql²/8). Stabilita la tensione di snervamento caratteristica f_yk e trovata la tensione di progetto f_yd, abbiamo individuato il modulo di resistenza a flessione minimo (W_x,min) e di conseguenza la sezione IPE.

- Dimensionamento pilastri

Per il predimensionamento dei pilastri abbiamo individuato l'area di influenza del pilastro più sollecitato e il carico agente su esso (peso del solaio e peso delle porzioni di travi portate). Da esso abbiamo calcolato lo sforzo normale massimo portato dal pilastro a terra.

Dallo sforzo nomale massimo (N_max) e dalla tensione di progetto (f_cd) abbiamo ricavato la sezione minima. Usando la luce libera di inflessione (l₀xβ) e il modulo di elasticità, abbiamo trovato la snellezza (λ) e da essa il valore minimo del raggio di inerzia minimo (ρ_min), necessario per evitare l'instabilità eulariana. Tenendo conto di A_min e ρ_min abbiamo scelto la sezione HE idonea.

Poiché per il dimensionamento della struttura sono state calcolate e sollecitazioni come se essa fosse isostatica, per la verifica è stato necessatio introddurre il telaio su SAP2000 per ricalcolare correttamente le sollecitazioni della struttura iperstatica.

- Analisi SAP 2000

- Verifica trave

σ = M/W < fd

Con i valori ottenuti da SAP abbiamo verificato che la tensione ottenuta (σ=M/W) fosse minore di quella di progetto (f_d). Poiché essa risultava notevolmente minore di quella progettata, abbiamo diminuito la sezione, scegliendo una sezione IPE più piccola che si avvicinasse maggiormente alla tensione ottenuta.

- Verifica pilastro

σ = N/A + M/W < fd

Confrontando la tensione ottenuta da SAP, la sezione del pilastro non risultava verificata (la tensione ottenuta era molto maggiore di quella di progetto), così abbiamo gradualmente modificato la sezione scegliendo profilati HE più grandi, fino ad ottenerne uno che risultava idoneo.

LEGNO:

- Analisi dei carichi:

Qs: carico strutturale

• fibrogesso γ = 11,5 kN/m³
• travetto legno lamellare γ = 3,8 kN/m³, interasse = 0,625 m

Qs = (11,5 x 0,03)x2 + (0,08 x 0,18 x 3,8 x 1/0,625) =  0,778 kN/m² 

Qp: carico permanente

• fibra di legno γ = 2,1 kN/m³
• malta di calce γ = 18 kN/m³ 
• pavimentazione parquet γ = 7,2 kN/m³ 
• impianti 0,5 kN/m
• tramezzi 1 kN/m

Qp = (0,06 x 2,1) + (0,054x 18) + (0,02 x 7,2) + 0,5 + 1 = 2,616 kN/m²

Qa: carico accidentale

Qa = 2 kN/m²

- Dimensionamento travi

Come per l'acciaio, abbiamo calcolato il momento massimo agente sulla trave. Dividendo quest'ultimo (M_max) per la tensione di progetto (f_d) abbiamo ricavato il modulo di resistenza a flessione minimo (W_x,min). Fissata la base, abbiamo ottenuto l'altezza minima necessaria a contrastare il momento, h=(6W/b)^1/2. Da questo valore abbiamo ricavato l'altezza della trave.

- Dimensionamento pilastri

E' stato calcolato lo sforzo normale portato a terra dal pilastro.

Dallo sforzo nomale massimo (N_max) e dalla tensione di progetto (f_cd) abbiamo ricavato la area di sezione minima. Usando la luce libera di inflessione (l₀xβ) e il modulo di elasticità, abbiamo trovato la snellezza (λ) e da essa il valore minimo del raggio di inerzia minimo (ρ_min) necessario per evitare l'instabilità eulariana. Da ρ_min abbiamo individuato la base, b=ρx12^1/2, e l'altezza minima, dalle quali abbiamo definito le dimensioni della sezione.

Poiché per il dimensionamento della struttura sono state calcolate e sollecitazioni come se essa fosse isostatica, per la verifica è stato necessatio introddurre il telaio su SAP2000 per ricalcolare correttamente le sollecitazioni della struttura iperstatica.

- Analisi SAP 2000

- Verifica trave

Con i valori ottenuti da SAP abbiamo verificato che la tensione ottenuta (σ=M/W) fosse minore di quella di progetto (f_d), come risulta.

- Verifica pilastro

Confrontando la tensione ottenuta da SAP, la sezione del pilastro non risultava verificata, così abbiamo modificato le dimensioni della sezione, ottenendo un valore della tensione più idoneo.

CALCESTRUZZO:

- Analisi dei carichi:

Qs: carico strutturale

• pignatta γ = 12 kN/m³
• calcestruzzo γ = 25 kN/m³, interasse = 0,5 m

Qs = (0,04 x 25) + (0,1 x 0,16 x 25) x 2 + (0,4 x 0,16 x 12) x 2 = 3,336 kN/m² 

Qp: carico permanente

• massetto γ = 18 kN/m³ 
• isolante acustico γ = 1 kN/m³ 
• pavimentazione cotto γ = 0,36 kN/m³ 
• impianti 0,5 kN/m
• tramezzi 1 kN/m

Qp = (0,04 x 18) + (0,013 x 1) + (0,025 x 0,36) + 0,5 + 1 = 1,86 kN/m²

Qa: carico accidentale

Qa = 2 kN/m²

- Dimensionamento travi

Come per il legno, abbiamo calcolato il momento massimo agente sulla trave. Quest'ultimo (M_max) è stato utilizzato per trovare l'altezza utile della trave, calcolata hu= r*(Mmax/b*fcd)^0.5, fissando precedentemente la base. Sommando questo valore al valore del copriferro è stata determinata l'altezza minima (hmin), successivamente ingegnerizzata. Trovata l'area della trave è stato calcolato il suo peso unitario ed è stato aggiunto questo valore al carico ultimo (qu). Il calcolo del peso proprio serve a capire se la base e l'altezza ingegnerizzata della propria trave resisterebbero anche sommando al carico ultimo il peso della stessa trave.

- Dimensionamento pilastri

E' stato calcolato lo sforzo normale portato a terra dal pilastro.

Dallo sforzo nomale massimo (N_max) e dalla tensione di progetto (f_cd) abbiamo ricavato la area di sezione minima. Usando la luce libera di inflessione (l₀xβ) e il modulo di elasticità, abbiamo trovato la snellezza (λ) e da essa il valore minimo del raggio di inerzia minimo (ρ_min) necessario per evitare l'instabilità eulariana. Da ρ_min abbiamo individuato la base, b=ρx12^1/2, e l'altezza minima, dalle quali abbiamo definito le dimensioni della sezione.

Poiché per il dimensionamento della struttura sono state calcolate e sollecitazioni come se essa fosse isostatica, per la verifica è stato necessatio introddurre il telaio su SAP2000 per ricalcolare correttamente le sollecitazioni della struttura iperstatica.

- Analisi SAP 2000

- Verifica trave

Con i valori ottenuti da SAP abbiamo verificato che la tensione ottenuta (σ=M/W) fosse minore di quella di progetto (f_d), come risulta.

- Verifica pilastro

Allo stesso modo risulta idonea la sezione scelta precedentemente in quanto la tensione ottenuta risulta minore rispetto a quella di progetto.

 

ESERCITAZIONE I_GRONDONA_PESCHIERA

 

L’ esercitazione 1 prevede il progetto di una struttura dimensionando gli elementi pilastri e travi; la struttura sarà studiata nei materiali: legno, acciaio, calcestruzzo.

 

Come prima cosa abbiamo definito il piano di carpenteria con:

-Luce: 6 m

-Interasse: 5 m

-Area di influenza: 30 m2

Il carico che imponiamo alla struttura è quello chiamato carico totale: Qu che è composta dalla somma del carico strutturale Qs ( carico dal peso proprio degli elementi portanti), il carico permanente Qp ( dato dal peso proprio degli elementi portati, non strutturali ) ed il carico accidentale Qa (carichi variabili nel tempo, accidentali, insieme ai carichi di esercizio).

Nel nostro caso avendo preso in esame un edificio con uffici avremo considerandolo aperto al pubblico.

• Qa=3[kn/m]​

​

Abbiamo anche definito subito il carico Qp come il carico somma di:

-intonaco: 0.3 kn/m2

-tramezzi: 1 kn/m2

-impianti: 0.5 kn/m2

-pavimento in rovere:peso per unità di volume=720kg/m3 che sappiamo equivalere a 7.2 kN/m3;

quindi qpavimento=7.2kn/m3*0.18m=1.3 kn/m2

- massetto: peso per unità di volume=1750kg/m3=17.5 kN/m3, lo spessore è di 0.04 m; quindi qmassetto=17.5kn/m3x0.04m=0.7 kn/m

•  Qp= (0.3+1+0.5+1.3+0.7)=3.8 [kN/m2]

Tutti questi carichi per Norma vengono moltiplicati da dei coefficienti a seconda che si studi la condizione di carico allo SLE (stato limite di esercizio) o allo SLU (stato limite ultimo). Nel caso di studio li consideriamo allo SLU e per la combinazione di carico fondamentale.

• Qu = γG1*Qs + γG2*Qp + γQ1*Qa

 

Questi dati ci servono per il dimensionamento degli elementi strutturali nei tre casi presi in esame: legno, acciao, calcestruzzo, che andremo ora ad analizzare.

CLS

Per calcolare il carico strutturale Qs del solaio in laterocemento calcoliamo il carico in un metro quadro di solaio:

[Vcls x γcls]x1/ i ={[(0.05 x 0.2)x 2 +(0.05 x 0.5)] x 2 }x 2.5 = 2.25 [kN/m² ]

[Vlat x γlat ]x1/ i =[(0.04 x 0.2)x 2 ]x 12= 1.92 [kN/m² ]

• Qs = 2.25 +1.92 = 4.17 [kN/m² ]
• Qu = 1.3 Qs + 1.5 Qp + 1.5 Qa = 5.42 +5.7 +4.5 = 15.62 [kN/m² ]

​1)TRAVI

Il foglio di calcolo relativo al cemento armato ha bisogno di più informazioni per dimensionare l’altezza della sezione rettangolare di una trave; questo può essere spiegato dal fatto che si tratta di un materiale non omogeneo, composto da calcestruzzo e da acciaio. Proprio per questo motivo in fase progettuale è necessario scegliere sia la resistenza caratteristica dell’acciaio (fyk) , che quella del calcestruzzo (fck).

**********

Una volta stabilite le tensioni di progetto abbiamo calcola l'altezza utile Hu e ẟ (la distanza fra il il baricentro dell’armatura e il filo del calcestruzzo teso) e la base per trovare l'altezza min di progetto.

• Hu =  r√Mmax/b

L'altezza min identifica la sezione min del calcestruzzo che va poi ingegnerizzata. Inoltre nel calcolo finale una volta trovata l'area della sezione di progetto va calcolato il peso della singola trave che andrà a modificare le soluzioni già trovate dei carichi e riverificati tutti i dati.

 

2)PILASTRI

Per dimensionare i pilastri abbiamo riportato i valori ottenuti su excel e calcolato lo sforzo Normale per tutti i piani del nostro telaio, considerando in questo calcolo il peso della trave stessa. In base al tipo di cls scelto abbiamo trovato la tensione di compressione caratteristica che ci permetterà di ricavare la tensione di design  dove αα è un fattore riduttivo che tiene conto degli effetti del tempo nel materiale pari a 0.85 e delle sue iterazioni con l'ambiente, mentre γm è un fattore di sicurezza che per le strutture in calcestruzzo è pari a 1.5.

• fck = 40 [Mpa]
• fcd = fck αα / γ m  

Una volta calcolato sforzo normale per la pilastrata e tensione di desing possiamo calcolare l'area e la base minima del pilastro. Infatti la tensione di design può essere considerata in fase di progetto uguale a Ϭ max 

• Ϭ max  = N/A   quindi    fd = N/A            Amin = N/ fd       

Abbiamo poi considerato l'instabilità euleriana a seguito dello sforzo di compressione che agisce sul pilastro e dunque anc la snellezza λ .

Dove

 

• N eul =(π² E Imin )/l₀²      l₀  =  β x l        I_min = A ρ²  min          λ = l₀ /ρmin

Possiamo quindi definire una tensione critica, poichè il carico critico è una forza di compressione che agisce sulla sezione, e metterla in relazione con la tensione massima

​ E' più sicuro pensare che la tensione all'interno dell'elemento raggiungerebbe per prima la resistenza a schiacciamento del materiale, poichè l 'instabilità euleriana è un fenomeno imprevedibile e dunque non si riesce a controllare.

Abbiamo poi verificato a presso-flessione il pilastro così ottenuto

• Ϭ_max= N/A + M/W_max   

 

_​Una volta calcolato la base e l'altezza del pilastro abbiamo verificato la struttura su sap2000

Dai diagrammi dello sforzo normale del telaio abbiamo ottenuto uno sforzo normale nel pilastro più sollecitato inferiore al volere ottenuto su excel e dunque la pilastrata è verificata.

 

LEGNO

In base alla composizione di questo solaio avremo per i travetti:

(V*γ )*1/i = {[(0.08*0.14) *1]*5.50 }*1/0.625 = 0.0616*1/0.625[kN/m²]

Per il pannello OSB:

(V*γ )*1/i = {[(0.03*0.625)*1*2]*8 }*1/0.625 = 0.3*1/0.625[kN/m²]

• Qs=0.578[kN/m²]
• Qu=1.3*Qs+1.5*Qp+1.5*Qa=10.95 [kN/m²]

1)DIMENSIONAMENTO DELLE TRAVI

Avendo definito il tipo di solaio ed i carichi li abbiamo riportati su excel utilizzandolo come foglio di calcolo; dopo aver definito il carico sull’interasse ed il momento massimo , in base al tipo di legno abbiamo trovato la tensione di progetto fd.

La tensione di progetto tiene conto delle azioni del tempo che influiscono sul materiale e sulla durata del carico , di un valore di sicurezza imposto dalla normativa e dalla classe di resistenza del legno scelto

• M_max= Qu*l²/8
• f_cd = K_mod f_yk  / γ _m  dove K_mod​ < 1

In fase di progetto una volta trovata la tensione di design f_cd ​è possibile ricavare H_min e modulo elastico di resistenza W_x

• H_min=[6*M_max*1000/(b*f_d)]^0.5
• Wx=b*h²/6

​

Per la verifica abbiamo controllato che la tensione massima Ϭ_max risultante sia minore di quella di progetto f_cd, risulta così verificata.

2)DIMENSIONAMENTO PILASTRI

Per quanto riguarda i pilastri abbiamo calcolato lo sforzo normale, definito la tensione di progetto, area minima della sezione.

Definiti modulo elastico e lunghezza libera di inflessione l_o = β x l  si calcolano: snellezza λ tenendo conto dell'instabilità euleriana , raggio d’inerzia e base minima ed altezza minima che ci aiutano a scegliere i valori che scegliamo per la base e l’altezza della sezione; calcoliamo anche l’area e inerzia di design come:

• A_design=b*h
• I_design=h*b³/12. 

La verifica si ottiene calcolando la tensione come lo sforzo normale sull’area, che deve essere minore della tensione di progetto: la sezione risulta verificata.

 

Abbiamo utilizzato SAP per verificare che i valori ottenuti sui fogli fossero corretti e per visualizzare gli schemi di carico sulla struttura ed i grafici dei carichi. Una volta disegnata la struttura, assegnato il materiale e definiti i carichi con la combinazione di carico finale, si vanno a definire le tipologie di sezioni; nel caso del legno le abbiamo definite come rettangolari in concrete ma abbiamo variato i valori per fare in modo che siano reali. Assegnate travi e pilastri abbiamo studiato la deformata ed i valori dei carichi e risulta che lo studio fatto in precedenza è corretto.

ACCIAIO

In base alla composizione del solaio abbiamo calcolato il carico strutturale sommando i carichi della soletta in calcestruzzo, della rete elettrosaldata e della lamiera grecata.

- Per la soletta in calcestruzzo :

•  γ_CLS=2300 [kg/m³]=23[kN/m³]
• V_CLS * γ_CLS = 23 *0.1 =2.3 [kN/m²]

- Per la rete elettrosaldata:

• γ_RETE=3.1 [kg/m²] = 0.031[kN/m²]

- Per la lamiera grecata:

• spessore = 1 mm
• γ_LAM = 9.58[kg/m²]=0.09[KN/m²]

Perciò il carico strutturale risulta:

• Qs=2.3 +0.031 +0.09 =2.421[KN/m²]

La combinazione di carico risulta quindi:

• Qu= 1.3Qs+1.5Qp+1.5Qa=13.35 [KN/m²]

​1)DIMENSIONAMENTO TRAVI

Per la verifica ci siamo calcolate sul foglio excel il momento massimo M_max

• M_max=Q_u*i*l²/8
• f_cd =  f_yk  / γ _m ​ dove  f_yk ​= 275 [N/mm²​]  γ _m=1.05
• Wx_min=M_max/fd

definita la tensione di progetto andiamo a calcolato il modulo elastico minimo: Wx_min=M_max/fd*1000. Da questo valore andiamo a scegliere una sezione IPE dal tabellario che rispetti il valore trovato; scegliamo la IPE400 e verifichiamo che la tensione, calcolata sostituendo al modulo elastico precedente quello di quest'ultima , sia minore di quella di progetto. Risulta perciò verificata.

2)DIMENSIONAMENTO PILASTRI

Per dimensionare i pilastri abbiamo calcolato lo sforzo normale dei pilastri ci calcoliamo la tensione di progetto e l’area minima.

• N=(Qs+Q_trave)*n_piani  
• A_min=N/f_yd
• λ=π*rad(E/f_yd)

​Ottenuto il raggio di inerzia minima è possibile ricavare il profilo HE corretto.

• ρ_MIN=β*l/λ
•  I_MIN=A_min* ρ_MIN ²

In base ai valori ottenuti scegliamo il profilato d’acciaio HEA260 e calcoleremo nuovamente la snellezza della trave sostituendo i valori:

• λ=β*l/ ρ_MIN

_​

La sezione è verificata avendo la tensione Ϭ_max=N/A_design<f_yd minore di quella di progetto.

​I risultati ottenuti sul modello di sap2000 danno uno sforzo normale sulla pilastrata inferiore rispetto a quelli ottenuti dunque i profili scelti sono verificati.

 

 

Esercitazione svolta da Rebecca Brock e Fracesca Di Gregorio.

Abbiamo scelto un unico telaio per le tre diverse tecnologie.

Acciaio

 

Calcolo dei carichi

Q_s: Carico strutturale

- Lamiera grecata + soletta
  q=1,65 kN/m²

- IPE 140
  γ = 12,9 kN/m
  N. travetti al metro: 3:7=0,42
  q = 0,42 x 12,9 = 5,418 kg/m² = 0,054 kN/m²

q_s=1,65+0,054=1,704 kN/m²

Q_p: Carico permanente

- Massetto
   γ =21 kN/m³
   q = 0,05 x 21 = 1,05 kN/m²

- Rivestimento Parquet
  γ = 7,2 kN/m3
  q = 0,02x 7,2 = 0,144 kN/m²

- Isolante
  γ =7,97 kN/m³
  q =0,04 x 7,97=0,3188  kN/m²

- Tramezzi
  q =1 kN/m²

- Impianti
  q = kN/m²

q_p= 3,0128 kN/m²

Q_a: Carico accidentale

q_a= 2 kN/m²

 

Dimensionamento travi

Su un foglio di calcolo Excel abbiamo inserito i valori trovati e calcolato la combinazione di carico al metro lineare, comprendente dei coefficienti di sicurezza. Poiché non ci è possibile trovare i valori delle azioni di carico per una struttura iperstatica coem questa, abbiamo individuato il momento massimo, M_max, come se fosse una trave appoggiata-appoggiata (M=ql²/8). Stabilita la tensione di snervamento caratteristica f_yke da qui trovata la tensione di progetto f_yd, abbiamo individuato il modulo di resistenza a flessione minimo (W_x,min) e di conseguenza la sezione IPE necessaria.

Dimensionamento pilastri

Per il predimensionamento dei pilastri abbiamo individuato l'area di influenza del pilastro più sollecitato (fig. 1) e il carico agente su esso (peso del solaio e peso delle porzioni di travi portate). Da esso abbiamo calcolato lo sforzo normale massimo, portato del pilastro a terra.

Dallo sforzo nomale massimo (N_max) e dalla tensione di progetto (f_cd) abbiamo ricavato la sezione minima. Usando la luce libera di inflessione (l₀xβ) e il modulo di elasticità, abbiamo trovato la snellezza (λ) e da essa il valore minimo del raggio di inerzia minimo (ρ_min) necessario per evitare l'instabilità eulariana. Tenendo conto di A_min e ρ_min abbiamo scelto la sezione HE idonea.

 

Calcolo SAP

Poiché per il dimensionamento della struttura sono state calcolate e sollecitazioni come se essa fosse isostatica, per la verifica è stato necessatio introddurre il telaio su SAP2000 per ricalcolare correttamente le sollecitazioni della struttura iperstatica.                                               

 Verifica Travi

Con i valori ottenuti da SAP abbiamo verificato che la tensione ottenuta (σ=M/W) fosse minore di quella di progetto (f_d). Poiché essa risultava minore di quella progettata, abbiamo diminuito la sezione, scegliendo una sezione IPE più piccola.

 

Verifica Pilastri

Confrontando la tensione ottenuta da SAP, somma di quella legata allo sforzo normale e di quella generata dal momento (σ=N/A+M/W), la sezione del pilastro non risultava verificata (la tensione ottenuta era molto maggiore di quella di progetto), così abbiamo gradualmente modificato la sezione scegliendo profilati HE man a mano più a grandi, fino ad ottenerne uno che risultava idoneo.

 

Legno

 

Calcolo dei carichi

Q_s: Carico strutturale

- Pannello di fibrogesso (x2)
   γ = 11,5 kN/m³
   q = 11,5 x 0,03 = 0,345 kN/m²

- Travetti
  γ = 3,8 kN/m³
  N. travetti al metro: 1:0,625=1,6
  q_t = 0,08 x 0,18 x 3,8 = 0,055 kN/m² per ogni travetto
  q =0,055 x 1,6 = 0,088  kN/m²

q_s=0,345+0,088 = 0,778 kN/m²

Q_p: Carico permanente

- Malta di calce
   γ = 18 kN/m³
   q =0,04 x 18 = 0,72 kN/m²

- Rivestimento Parquet
  γ = 7,2 kN/m3
  q = 0,02 x 7,2 = 0,144 kN/m²

- Fibra di legno
  γ = 2,1 kN/m³
  q = 0,06 x 2,1 =0,252  kN/m²

- Tramezzi
  q =1 kN/m²

- Impianti
  q =0,5 kN/m²

q_p= 2,616 kN/m²

Q_a: Carico accidentale

q_a= 2 kN/m²

 

Dimensionamento travi

Come per l'acciaio, abbiamo calcolato il momento massimo agente sulla trave. Dividendo quest'ultimo (M_max) per la tensione di progetto (f_d) abbiamo ricavato il modulo di resistenza a flessione minimo (W_x,min). Fissata la base, abbiamo ottenuto l'altezza minima necessaria a contrastare il momento, h=(6W/b)^1/2. Da questo valore abbiamo impostato l'altezza della trave.

Dimensionamento pilastri

Come già fatto per l'acciaio, abbiamo calcolato lo sforzo normale massimo, portato del pilastro a terra.

Dallo sforzo nomale massimo (N_max) e dalla tensione di progetto (f_cd) abbiamo ricavato la area di sezione minima. Usando la luce libera di inflessione (l₀xβ) e il modulo di elasticità, abbiamo trovato la snellezza (λ) e da essa il valore minimo del raggio di inerzia minimo (ρ_min) necessario per evitare l'instabilità eulariana. Da ρ_min abbiamo determinato la base (b=ρx12^1/2) e l'altezza minima, dalle quali abbiamo definito le dimensioni della sezione.

Calcolo SAP

Poiché per il dimensionamento della struttura sono state calcolate e sollecitazioni come se essa fosse isostatica, per la verifica è stato necessatio introddurre il telaio su SAP2000 per ricalcolare correttamente le sollecitazioni della struttura iperstatica.

 Verifica Travi

Con i valori ottenuti da SAP abbiamo verificato che la tensione ottenuta (σ=M/W) fosse minore di quella di progetto (f_d), come ci risulta.

 

Verifica Pilastri

Confrontando la tensione ottenuta da SAP, somma di quella legata allo sforzo normale e di quella generata dal momento (σ=N/A+M/W), la sezione del pilastro non risultava verificata, così abbiamo modificato le dimensioni della sezione, ottenendo un valore della tensione idoneo.

 

Calcestruzzo

 

Calcolo dei carichi

Q_s: Carico strutturale

- Pignatte
   γ = 12 kN/m³
   q = 2 x 0,4 x 12 = 1,536 kN/m²

- Travetti in calcestruzzo
  γ = 25 kN/m³
  q = 25 x 2 x 0,16 x 0,1 = 0,8  kN/m²

- Soletta in calcestruzzo
  γ = 25 kN/m³
  q = 25 x 0,4 = 10 kN/m²

q_s =3,336 kN/m²

Q_p: Carico permanente

- Massetto
   γ = 18 kN/m³
   q =0,04 x 18 = 0,72 kN/m²

- Isolamento acustico
  γ = 1 kN/m³
  q = 0,013 x 1 = 0,013 kN/m²

- Rivestimento
  q = 0,36 kN/m²

- Tramezzi
 q =1 kN/m²

- Impianti

  q =1,86 kN/m²

q_p= 2,616 kN/m²

Q_a: Carico accidentale

q_a= 2 kN/m²

 

Dimensionamento travi

Dopo aver calcolato il momento massimo agente sulla trave, abbiamo ricavato i valori delle tensioni di progetto del calcestruzzo (f_cd) e dell'acciaio di armatura (f_ck). Con questi è stato ricavato α, attraverso il quale abbiamo ottenuto r. Fissata la base della sezione, con r, il momento massimo M_max e la tensione di progetto del calcestruzzo f_cd, è stata calcolata l'altezza utile h_u, alla quale abbiamo aggiunto d, la distanza dei ferri dal bordo della sezione, per conoscere l'alteza minima H_min. Regolarizzata l'altezza (H), abbiamo calcolato l'area della sezione e, conoscendo il peso specifico del calcestruzzo, è stato determinato il peso unitario. Quest'ultimo è poi stato aggiunto (con un margine di sicurezza) al carico ultimo q_u per verificare che la sezione fosse in grado di sostenere il carico del solaio e quello del peso proprio (considerevole nel caso del calcesruzzo armato).

Dimensionamento pilastri

Come precedentemente, si è calcolato lo sforzo normale massimo, portato del pilastro a terra.

Così come per il pilastro in legno, dallo sforzo nomale massimo (N_max) e dalla tensione di progetto (f_cd) abbiamo ricavato la area di sezione minima. Usando la luce libera di inflessione (l₀xβ) e il modulo di elasticità del calcestruzzo E, abbiamo trovato la snellezza (λ) e da essa il valore minimo del raggio di inerzia minimo (ρ_min) necessario per evitare l'instabilità eulariana. Da ρ_min abbiamo determinato la base (b=ρx12^1/2) e l'altezza minima, dalle quali abbiamo definito le dimensioni della sezione.

Calcolo SAP

 

Verifica travi

Con i valori ottenuti da SAP la tensione ottenuta (σ=M/W) risultava maggiore di quella di progetto (f_d), così è stata aumentata l'altezza della sezione (dimensione che più influisce sul modulo di resistenza a flessione) ed è stata ricavata una tensione idonea.

Verifica pilastri

Confrontando la tensione ottenuta da SAP, somma di quella legata allo sforzo normale e di quella generata dal momento (σ=N/A+M/W), la sezione del pilastro risultava verificata.

 

 

 

La prima esercitazione prevede l’analisi di un telaio a pilastrata con una tecnologia in cemento armato, acciaio e legno. Le immagini che seguono descrivono il telaio preso in esame: 

Fig. 01 Pianta

Fig. 02 Prospetto 

Abbiamo realizzato due analisi parallele, una sul progetto della trave e una sul progetto del pilastro attraverso i fogli di calcolo Excel, in entrambe i casi scegliendo quello più sollecitato, per poi inserire i dati ottenuti su SAP2000.

Definito l’interasse, abbiamo analizzato la combinazione di carico q_u, ottenuta come somma delle singole componenti di carico q_s, q_p e q_a, che sono rispettivamente il peso della struttura a mq (che dipende dalla tecnologia usata), il peso dei sovraccarichi permanenti e il carico accidentale dovuto alla destinazione d’uso (uffici aperti al pubblico), ognuno di essi moltiplicato per un fattore di sicurezza, preso dalla normativa.

In figura illustriamo i tre solai che abbiamo scelto per le diverse tecnologie.

Solaio in Cemento armato

Solaio in acciaio

Solaio in legno 

 

Nel primo foglio Excel di calcolo della trave abbiamo quindi una prima pagina in cui abbiamo portato parallelamente l’analisi delle tre tecnologie per arrivare alla combinazione di carico che ha la seguente formula:

q_u=γ_sq_s+γ_pq_p+γ_aq_a 

_dove
γ_s=1.3 
γp = 1.5 
γ_a=1.5

Questo carico ci fornisce un dato al mq, ma per effettuare l’analisi lungo la trave moltiplichiamo questa grandezza per l’interasse per ottenere quindi una grandezza espressa in kN/m. Come risultato di questa prima pagina abbiamo il momento massimo su questa trave, per cui aggiungiamo l’informazione relativa alla luce e, ipotizzando il modello di funzionamento a trave appoggiata, calcoliamo il valore di M_max con la seguente formula:

M_max=ql²/8

Con questo dato di partenza abbiamo sviluppato tre fogli di calcolo per le tre tecnologie per  il progetto della trave ed abbiamo ottenuto come dato in uscita il valore di base e altezza, quindi definito la sezione.

In particolare per il cemento armato abbiamo stabilito una tensione caratteristica f_y,k di 450 MPa, l’abbiamo divisa per il coefficiente di sicurezza per ottenere la tensione di progetto f_y,d per i tondini di acciaio; abbiamo poi preso f_c,k, cioè la tensione caratteristica del calcestruzzo, moltiplicandola per il coefficiente αα, che tiene conto dell’interazione del tempo e dell’ambiente con la struttura, e dividendolaper il coefficiente γ di sicurezza, otteniamo la tensione f_c,d di progetto.

Per la definizione della sezione effettuiamo i seguenti passaggi:

• Calcoliamo il valore di β come:
  β =  f_c,d / ( f_c,d + ( f_c,d / 15)) 
• Calcoliamo il valore di r come:
  r = (2/ β (1 - (β/3))  ^0.5
• Ipotizziamo una base b pari a 30 cm 
• Calcoliamo l'altezza utile con la seguente formula:
  h_u = r (M_max / f_c,d b) ^ 0.5
• Inseriamo un copri ferro δ pari a 5 cm 
• Calcoliamo l’altezza effettiva della sezione sommando l’altezza utile con la dimensione del copriferro ed otteniamo un’altezza ingegnerizzata pari a 40 cm
• Calcoliamo l’area della sezione della trave e il suo peso unitario moltiplicando l’area per il peso specifico del calcestruzzo (30 x 40 cm). 

Per quanto riguarda l’acciaio siamo partite dal momento massimo agente sulla trave, abbiamo stabilito la f_y,k pari a 275 MPa, la tensione caratteristica di snervamento, da dividere per il coefficiente di sicurezza pari a 1.05 che ci permette di ottenere la tensione di progetto dell’acciaio, f_y,d. Abbiamo successivamente calcolato il modulo di resistenza a flessione con la seguente formula:

W_x,min = M_max / f_y,d

Con questo dato possiamo rintracciare nel sagomario una IPE che abbia un W_x,min maggiore (IPE 330).  

Allo stesso modo per il legno siamo partite dal momento massimo agente, per poi stabilire la tensione caratteristica f_m,k (C30). Abbiamo poi moltiplicato quest'ultima per il coefficiente di sicurezza k_mod, che tiene conto dell’umidità e dell’effetto della durata del carico, e divisa per un coefficiente di sicurezza pari a 1.50 al fine di ottenere la tensione di progetto fd. 

f_d = ( f_m,k / γ_m ) k_mod

Ipotizzando anche in questo caso una base, calcoliamo l'altezza utile con la seguente formula: 

h_u = ( 6 M_max / b f_d )

Ingegnerizzando questo valore otteniamo il valore finale dell'altezza della sezione (30 x 40 cm). 

 

Concluso il progetto delle travi, abbiamo affrontato il progetto dei pilastri nelle tre tecnologie.

 Come prima analisi abbiamo realizzato un foglio di calcolo per stabilire lo sforzo normale agente sul pilastro, dato che poi diventerà nelle successive tre pagine di calcolo il dato di partenza per la definizione della sezione. In particolare abbiamo definito:

• L’area di influenza A_inf , che otteniamo con la formula
  A_inf = ((L_a + L_b) / 2) + ((L_c + L_d) / 2)
• Fissiamo i tre γ pari a 25 kN/m³ per il calcestruzzo, 78.5 kN/m³ per l’acciaio e  6 kN/m³ per il legno. 
• Calcoliamo l’area della trave e quindi il peso, moltiplicando l’area della trave per la luce maggiore (per ottenere il peso delle travi principali) e la stessa area per la luce minore (per ottenere il peso delle travi secondarie), questa somma, moltiplicata per il peso specifico, ci fornisce il peso delle travi su un mq di solaio. 
• Calcoliamo la combinazione di carico, come abbiamo fatto precedentemente nelle travi con la formula 
  q_u=γ_sq_s+γ_pq_p+γ_aq_a 
• Calcoliamo il valore di sforzo normale agente su un piano moltiplicando l’area di influenza per la combinazione di carico allo stato limite ultimo e lo sommiamo al peso delle travi, ottenendo il valore concentrato di N (kN)
  N = (A_inf q_u) + qt
• Stabilito il numero dei piani della nostra struttura (4) otteniamo il valore di massima sollecitazione a compressione agente sul pilastro moltiplicando l’N agente su un piano per il numero di piani. Con questo dato entriamo nel foglio di calcolo della progettazione dei pilastri nelle tre tecnologie. 

La progettazione della sezione di un pilastro in calcestruzzo prevede oltre la progettazione a compressione anche una verifica a pressoflessione. Riportato il valore di N_max:

• Stabiliamo la classe di resistenza del calcestruzzo (C50/60) e moltiplicando il valore della resistenza caratteristica per un coefficiente αα (0.85), che tiene conto degli effetti del tempo, e dividendolo per il coefficiente di sicurezza che tiene conto del processo produttivo γ_m pari a 1.5 otteniamo la resistenza di progetto. 
• Calcoliamo l’area minima considerando la formula inversa di 
  σ = N / A  
  quindi  A_min = N_max / f_c,d
• Stabiliamo il modulo elastico E, l’altezza del pilastro L e il coefficiente β che tiene conto della condizione di vincolo della struttura.
• Calcoliamo la snellezza come
  λ = ((π² E) / f_c,d ) ^ 0.5
• Calcoliamo il ρ_min cioè il raggio giratore d’inerzia come
  ρ_min = Lβ / λ
• Stabiliamo la base minima 
  b_mim = ρ_min (12) ^ 0.5
• Quindi otteniamo l’altezza minima dividendo l’area minima per la base minima; ingegnerizziamo le dimensioni ottenute, calcoliamo l’area della sezione, il momento d’inerzia I e il modulo di resistenza W pari a 
  W_max = (bh²) / 6 
• Per la sezione in calcestruzzo effettuiamo la verifica a pressoflessione confrontando la σ_max  con la tensione di progetto f_cd 
  σ_max = (N_max / A) + (M_max​ / W_max)  < f_cd  

Il valore di M_max è calcolato come M_t = (q_t L_p²) / 12 e q_t è il valore uscente dal progetto della trave in calcestruzzo e che è pari alla combinazione di carico per l’interasse principale. 

​

Per quanto riguarda il progetto del pilastro in acciaio siamo partite dallo sforzo di compressione massimo, la definizione della classe di resistenza f_y,k (235 MPa), che moltiplicato per il coefficiente di sicurezza (1.05) ci consente di calcolare la tensione di progetto f_y,d. Successivamente: 

• Calcoliamo l’area minima dividendo lo sforzo N massimo per la tensione di progetto  A_min = N_max / f_y,d
• Stabiliamo il modulo elastico E (210000 MPa), il β che descrive i vincoli e l’altezza del pilastro (3.50 m).  
• Calcoliamo la snellezza minima λ_min
  λ = ((π² E) / f_y,d ) ^ 0.5
• Calcoliamo il ρ_min 
  ρ_min = Lβ / λ 
• A differenza del calcestruzzo, nell’acciaio non calcoliamo l’altezza utile, ma cerchiamo il valore d’inerzia minimo che possiamo usare per definire sui sagomari una sezione HEA, con la condizione che il valore dell'inerzia della sezione scelta sia maggiore di quella di progetto
  I_min = A ρ_min² 
• Stabilito il profilo HEA (200) inseriamo nella tabella i valori che ne descrivono la sezione, quindi l’area, l’inerzia e il raggio giratore d’inerzia. Verifichiamo poi che la snellezza che otteniamo sia minore della snellezza minima che abbiamo calcolato precedentemente. 

Il progetto del pilastro in legno segue le seguenti fasi.

• Riportato il valore di sforzo normale massimo, scegliendo la classe di resistenza (C24), riportiamo il valore della tensione caratteristica, che moltiplicata per il coefficiente k_mod,  che tiene conto dell’umidità e dell’effetto della durata del carico, e diviso per il coefficiente di sicurezza γ_m, ci fornisce la tensione di progetto.
• Dividendo lo sforzo normale agente per la tensione di progetto otteniamo l’area minima della sezione.
• Stabilito il modulo elastico E, il coefficiente β e l’altezza del pilastro L, calcoliamo quindi la snellezza massima λ_max, il ρ_min e otteniamo
  b_mim = ρ_min (12) ^ 0.5
• Stabiliamo una base ingegnerizzata, ricaviamo, dividendo l’area minima per quest’ultima base, un'altezza ed ingegnerizziamo anch’essa. Stabilita quindi la sezione otteniamo l’area di progetto e il valore dell’inerzia.

   

Finita la fase di calcolo su Excel abbiamo impostato questo stesso telaio, nelle tre tecnologie, nel software SAP2000, che ci consente di poter confrontare le sezioni progettate e i relativi diagrammi delle sollecitazioni con ciò che abbiamo ottenuto dai fogli di calcolo.

I diagrammi che abbiamo ottenuto sono i seguenti per il cemento armato:  

Schema strutturale 

Diagramma del Momento sulle travi (combinazione che considera il vento) 

Diagramma dello sforzo normale sui pilastri (combinazione che considera il vento) 

 

I diagrammi seguenti illustrano il comportamento del telaio con travi e pilastri in acciaio: 

Schema strutturale

Diagramma del Momento sulle travi (combinazione che considera il vento)  

Diagramma dello sforzo Normale sui pilastri (combinazione che considera il vento)  

 

I diagrammi seguenti illustrano il comportamento del telaio con travi e pilastri in legno.  

Schema strutturale

Diagramma del momento sulle travi (combinazione che considera il vento)  

Diagramma dello sforzo normale sui pilastri (combinazione che considera il vento)  

 

Le immagini precedenti mostrano la combinazione di carico che include anche la componente di carico orizzontale dovuta alla presenza del vento, che  aggiungiamo su SAP200 come carico orizzontale nella direzione Y (perpendicolare alla struttura) pari a:
F_vento = 0.70 i
dove i è Dove i è l’interasse sul prospetto minore, illustrato in figura (dimensione di una pressione kN/m, carico lineare) 

Abbiamo considerato le sollecitazioni di momento e compressione per le tre tecnologie in presenza di vento. Analizzando ciò che accade escludendo l'azione del vento possiamo osservare che i valori che otteniamo si avvicinano di più a quelli che risultano dal foglio di calcolo Excel, soprattutto per il legno e l’acciaio. Un’altra differenza è l’approssimazione che sul foglio di calcolo consideriamo per definire i vincoli, che su SAP diventano più rigorosi.

Esercitazione eseguita con Jessica Sordi 

L'esercitazione prevede il dimensionamento della Trave e del Pilastro più sollecitati di un telaio, considerando tre soluzioni tecnologiche differenti: Legno, Acciaio e Cls armato.

LEGNO

Dopo aver scelto la tipologia di solaio, iniziamo calcolando i carichi che agiscono su di esso.

Questi si dividono in:

qs, carichi strutturali, dati da tutti gli elementi che hanno funzione strutturale

qp, carichi permanenti, dati da tutti gli elementi presenti nel solaio ma che non hanno funzione strutturale

qa, carichi accidentali, dati dalla normativa, in questo caso qa=2kN/m² perchè si considera la destinazione d'uso abitativa

il valore dei carichi si ottiene moltiplicando il volume di tutti gli elementi, a m², per il loro peso specifico, in particolare:

qs:

Travetto in legno: 0,16 kN/m²

Tavolato in legno: 0,20 kN/m²

Gettata in CLS: 1,00 kN/m²

TOT: 1,36 kN/m²

qp:

Pavimento: 0,02mx0,6kN/m³=0,012 kN/m² 

Allettamento: 0,06mx19kN/m³=1,14 kN/m²

In questo caso si tiene conto anche dell'incidenza dei tramezzi e degli impianti, per un valore pari a 2,5 kN/m²

TOT: 2,68 kN/Mm²

TRAVE

Fissata la luce il foglio calcola il momento massimo della trave, pari a q_ul²/8

 

Ora scelgo la classe di resistenza del materiale, in questo caso C24, dove F_mk=24 N/mm² .

conoscendo F_mk, il foglio calcola la tensione di progetto che è pari a F_md .

K_mod è un fattore che tiene conto del degrado del materiale.

Trovata la resistenza di progetto posso fissare una base, presa da un profilario e trovo il profilo con resistenza subito maggiore a quella trovata.

Fissata la base, i dati mi permettono di trovare l'altezza minima, infine la ingegnerizzo.

PILASTRO

Parto calcolando l'area d'influenza del pilastro e inserendo l'area della trave precedentemente trovata.

Assegnato il peso specifico del materiale, in particolare 6 kN/m³ (Abete rosso) posso calcolare il peso delle travi agenti sul pilastro.

Avendo il carico ed il peso delle travi agenti sul pilastro, il foglio calcola inizialmente lo sforzo normale per un piano.

Poi aggiungendo il numero dei piani trovo lo sforzo normale massimo, N_max 

Dato N_max e F_md posso trovare l'area minima che il pilastro deve avere per sopportare i carichi agenti.

Fissati E ( dato dalla classe di resistenza) , la luce e ß (coefficente che dipende dalla condizione di vincolo) posso trovare: la snellezza, il raggio d'inerzia minimo che mi permetteranno poi di trovare la base e l'altezza minima della sezione del pilastro. 

Ora posso ingegnerizzare, ovvero dare alla base e all'altezza dei valori reali che si possono trovare sul mercato.

Ora calcolo A_design , ovvero l'area della sezione progettata che, per essere verificata deve essere maggiore dell'area minima trovata in precedenza.

In questo caso A_min < A_design , quindi la sezione è verificata.

 

ACCIAIO

Si procede con il calcolo dei carichi 

qs: 1,8 kN/m²

qp: 2,15 kN/m²

TRAVE

Trovo il momento massimo della trave come q_ul²/8.

Scelta la classe di resistenza del materiale, S275, avrò f_yk=275 N/mm²

Il foglio calcola la tensione massima di progetto f_yd

Nel caso dell'acciaio è necessaria una verifica a flessione della trave e solo trovando il modulo di resitenza a flessione minima, W_min, potrò scegliere il profilo in grado di sopportare i carichi agenti

Trovata W_min, la ingegnerizzo, andando sul tabulario e prendendo il profilo con resistenza a flessine subito maggiore a quella trovata. 

In questo caso si tratta di un IPE400

PILASTRO

Come visto in precedenza, il foglio calcola l'area d'influenza del pilastro, inserendo le luci, e il peso delle travi, inserendo il peso specifico del materiale e l'area della trave.

Successivamente il foglio calcolerà il carico ultimo q_u 

Con i dati inseriti il foglio calcolerà prima lo sforzo normale per un piano, poi per tutti i piani della struttura (Nmax)

Dato Nmax e f_yk il foglio calcolerà f_yd e A_min

Fissati E, la luce e ß posso trovare: la snellezza, il raggio d'inerzia minimo che mi permetteranno poi di trovare il momento l'inerzia minimo della sezione del pilastro.

Con i dati ottenuti dal profilario delle travi HE trovo il profilo con I_min appena superiore a quello trovato, facendo attenzione che l'area della sezione sia comunque superiore a quella trovata in precedenza.

In base a queste considerazioni il profilo trovato per il pilastro è HEA120

CALCESTRUZZO

Trovo i carichi

qs:2,5 kM/m²

qp:3,85 kN/m²

TRAVE

Il foglio calcolerà il carico ultimo q_u e, successivamente, inserendo la luce, M_max

 Nel caso del calcestruzzo il dimensionamento è diverso perchè nella trave abbiamo due materiali, il calcestruzzo e l'acciaio (i tondini d'armatura), quindi nella progettazione della trave bisogna tener conto di due resistenze:

f_yk la resistenza caratteristica a flessione dell'acciaio

f_ck la resistenza caratteristica a compressione del calcestruzzo

Il foglio calcolerà le due resistenze di progetto f_yd e f_cd

Successivamente calcolerà due fattori: r e alfa , che sono due coefficenti che ci permettono di calcolare l'altezza utile, cioè l'altezza reagente della sezione, che si basa sull'ipotesi della conservazione delle sezioni piane e sul fatto che il calcestruzzo reagisca solo a compressione.

Fissata la base il foglio calcolerà h_u.

Si troverà infine l'altezza minima della trave, aggiungendo ad h_u il contributo del copriferro e del raggio del tondino.

Infine la ingegnierizziamo.

PILASTRO

Il procedimento iniziale del pilastro è uguale agli altri materiali presi in considerazione in precedenza.

Calcolati A_inf,P_travi e q_u il foglio calcolerà, prima N1piano (relativo ad un piano solo) e, successivamente, Nmax.

Con N_max e f_cd il foglio calcola A_min

Fissati E, la luce e ß, il foglio calcolerà, prima la snellezza ed il raggio d'inerzia minima, con i quali, successivamente, il foglio calcolerà la base e l'altezza minime della sezione del pilastro.

Ora si ingegnerizza la sezione, trovando b_design, h_design ed infine A_design

Il pilastro deve essere sottoposto alla verifica di presso-flessione, per questo motivo, inserendo il momento massimo generato dalla struttura precedentemente analizzata, 

si procede al calcolo del modulo di resistenza a flessione massimo e, successivamente, della tensione massima ammissibile, che per essere verificata non deve essere maggiore della tensione di progetto del materiale.

 

 

.

TELAIO IN ACCIAIO

 

1)

Disegno il telaio della mia struttura, che avrà una luce massima di 8 m e un'altezza di tre piani. 

Scelgo la tecnologia del solaio, composta da travetti in travi di acciaio IPE140, sormontati da una pacchetto composto da una lamiera gregata e da una soletta. Il carico strutturale sarà calcolato dal prodotto tra volume e peso specifico dei materiali del solaio a metro quadro. 2)

                     qs=(V1* γ1 + ... + Vn* γn)*1/i 

Il carico permanente sarà calcolat con lo stesso criterio, considerando la pavimentazione del solaio, isolante, massetto, pavimentazione, a cui saranno aggiunti i carichi di 1kN/m2 per i tramezzi, e di 0,5 kN/m2 per gli impianti.

Il dato del carico accidentale lo leggo sempre nella normativa vigente, e nel nostro caso è pari a 2 kN/m2

Posso trovare il qu, dalla seguente somma

                     qu=(1,3*qs+1,5*qp+1,5*qa)

il peso sarà maggiorato da coefficenti di sicurezza che mi obbligano ad aumentare il valore del mio peso considerato.

 

3) 

Il peso a metro quadro del solaio, mi serve nel predimensionamento della trave, in quanto questo, moltiplicato per l'interasse di interessa e poi spalmato per la lunghezza della trave mi fornisce il carico distribuito sulla mia trave.

Per cui la prima operazione da fare sarà quella di trovare q, espresso in kN/m. Per calcolare il Momento massimo della trave, che considero come se fosse una trave doppiamente appoggiata, applicherò la formula

                         M=(q*l2)/8 (kN*m)

Una volta trovato M max, per scegliere il profilo più adeguato da utilizzare per predimensionare la mia trave, utilizzerò la formula fd=M/W , dove fd, è la tensione di progetto che io scelgo dal materiale. Nello specifico fd si calcola conoscendo la tensione di snervamento dell’acciaio prescelto,considerando di un coefficiente parziale di sicurezza γs,  pari a 1,05.

                         fd=fk/1,05

In questo modo posso ricavare il modulo di resistenza a flessione

                         W=M/fd

scegliendo un W uguale o maggiore da una tabella di profilati IPE, avrò ottenuto un primo dimensionamento della mia trave. 

4)

Il dimensionamento del pilastro parte da ragionamenti simili, in questo caso conosco già il peso del mio solaio e metro quadro, e devo fissare altri valori. Primo tra tutti l'area di influenza del solaio sul pilastro più sollecitato, che per l'appunto sarà quello su cui grava un'area di influenza maggiore. Avendo poi scelto una trave, aggiungo al peso qu, anche il peso lineare della trave scelta, moltiplicato per i metri degli interassi all'interno sempre dell'area di influenza interessata.

Ora, conoscendo anche il numero dei piani, posso calcolare lo sforzo N del pilastro più sollecitato con la seguente formula    

                       Nmax=((qu*Ainf)*qt)*np

Trovato lo sforzo normale, posso trovare una prima area minima con la seguente formula 

                       Amin=Nmax/fd

Tuttavia, l'area di questo pilastro terrebbe conto solo della compressione esercitata sul pilastro, e non della flessione a cui questo viene sottoposto con un carico verticale. Per non ovviare a questo problema, dovrò quindi tenere conto anche del carico critico Euleriano, e di conseguenza non avrò solo un'area minima, ma anche un'altro valore, cioè, quello del momento di inerzia minimo affinché la sezione del pilastro consenta a quest'ultimo di resistere a flessione.

Sapendo che la formula del momento di inerzia minimo è la seguente, posso calcolarlo, sapendo che y è un coefficiente di sicurezza, E il modulo elastico, e l0, la lunghezza libera di inflessione, che conosco conoscenso i vincoli agli estremi del mio pilastro.

                     Jmin > N*l0/γ*π^2*E

Altro valore da tenere in considerazione è il raggio di inerzia minimo che ricavo conoscendo l0 e la snellezza, in quanto la snellezza λ è il raggorto tra la lunghezza libera di inflessione e il raggio di inerzia minimo. E sapendo che la normativa mi impone di porre λ non minore di 200, scrivo:

                     imin > 200/l0

Dalla scelta del momento di inerzia minimo, scelgo nella tabella, il pilastro HEA con le caratteristiche corrispondenti ai tre valori minimi che devo soddisfare.

Il primo pilastro scelto, HEA140, tuttavia non soddisfa uno dei valori richiesti, come si vede nella figura 04.

Si passa alla scelta di un secondo pilastro, HEA200, che apparentemente soddisfa le nostre richieste prestazionali.

 

5)

Passo alla fase in cui devo verificare se effettivamente gli elementi strutturali predimensionati soddisfano o meno le reali richieste prestazionali.

per la trave utilizzo la formula 

                    σ=Mmax/W 

La trave è verificata se fd, cioè la tensione di progetto è maggiore della tensione trovata 

                    fd>σ

Nel nostro caso la trave è stata sovradimensionata, avendo considerato un momento massimo, quello della trave doppiamente appoggiata, di molto superiore al momento massimo reale trovato su sap, corrispondente al modello di una trave a doppio incastro.

La verifica per il pilastro utilizza invece la seguente formula dovendo tener conto sia dello sforzo normale sia della flessione

                   σ=(Nmax/Ad)+(Mmax/W)

Il pilastro preso in considerazione non soddisfa la verifica, in quanto  σ>>fd

 

Si cambiano quindi i paramenti presi in considerazione per il dimensionamento del pilastro, fino a trovare uno adeguato.

 

TELAIO IN LEGNO

 

1) Disegno il mio telaio, che avrà una luce massima di 7 m e un'altezza di tre piani.

2) Scelgo la tecnologia del mio solaio come fatto precedentmente e calcolo il suo carico 

                    qs=(V1* γ1 + ... + Vn* γn)*1/i 

Vi aggiungo i carichi permanenti e accidentali, e trovo qu sommando.

                    qu=(1,3*qs+1,5*qp+1,5*qa) 

3) Con il qu, moltiplicato per l'interasse, posso trovare M max della trave, considerandola sempre come se fosse una trave doppiamente appoggiata

                    M=(q*l2)/8 (kN*m)

4) Per dimensionare la sezione della trave necessaria, devo applicare al seguente formula 

                    h= l * ((3/4)*q/(b*fd))^0,5

Ho tutte i dati, la base la inserisco io come variabile, mentre fd, è la tensione di progetto, che ricavo dalla scelta del materiale. Nello specifico dalla sua tensione caratteristica, con la seguente formula:

                   fd=kmod*fk/γ

dove kmod è un coefficiente che tiene conto del tempo, quindi dell'agire di alcune condizioni quali l'umidità sulla resistenza del materiale, pari a 0,8, mentre gamma è un'altro coefficiente di sicurezza, pari a 1,5.

Fissata la mia base, trovo la rispettiva altezza, e le ingegnerizzo per ricavare una trave reale.

5) Per il dimensionamento dei pilastri, si seguono gli stessi criteri di cui ci siamo serviti per predimensionare il pilastro in acciaio, quindi considereremo la resistenza sia a compressione, sia a presso/flessione. 

Considero quindi l'area minima necessaria ricavando lo sforzo N massimo, che trovo con la somma:

                    Nmax = ((qu*Ainf) + qt)* np

Dove qt è il peso delle travi, e np, il numero di piani del mio edificio.

Da qui trovo l'Area minima per resistere alla compressione 

Diverso è il caso, analogamente per il primo calcolo che abbiamo considerato per la struttura in acciaio, per determinare l'area necessaria, in funziona del momento di inerzia minimo della sua sezione, nel caso in cui consideriamo il pilastro flettersi per effetto della compressione di punta esercitato su di esso.

considero per ricavare il mio momento di inerzia necessario, il raggio minimo di inerzia, che desumo dalla formula:

                      ρmin=l0/λ

dove l0 è la lunghezza libera di inflessione, seguendo gli stessi ragionamenti per l'acciaio.

Posso allora ricavare λ dalla seguente formula:

                     λ=π *(E/fd)^0,5

I restanti dati, sono dati che conosco e che determino io.

conoscendo quindi il raggio minimo di inerzia, posso desumere la base, quindi il lato più corto del pilastro, necessario per raggiungere l'area interessata.

                     b=2*((3)^0,5)*ρmin

Ora posso trovare l'altro lato, mettendo in rapporto tra loro l'area trovata inizialmente e la base.

6)

Una volta trovati su sap i momenti massimi reali, faccio la verifica tensionale, utilizzando le stesse formule usate per il dimensionamento del telaio in acciaio, e se le sezioni non sono verificate, le cambio fino ad ottenere un risultato corretto.

 

TELAIO IN C.A.

1) Si parte come nei casi precedenti dal disegno del telaio, che in pianta avrà le seguenti dimensioni.

2) Scelgo la tecnologia del mio solaio come fatto precedentmente e calcolo il suo carico 

                    qs=(V1* γ1 + ... + Vn* γn)*1/i 

Vi aggiungo i carichi permanenti e accidentali, e trovo qu sommando.

                    qu=(1,3*qs+1,5*qp+1,5*qa) 

3) Con il qu, moltiplicato per l'interasse, posso trovare M max della trave, considerandola sempre come se fosse una trave doppiamente appoggiata

                    M=(q*l2)/8 (kN*m)

4) Il dimensionamento della trave, cambia di impostazione rispetto a quella applicata nel caso del telaio di legno Nel caso del calcestruzzo, ho più variabili da considerare, date dal fatto anche che sono in presenza di due materiali aventi caratteristiche differenti tra loro, e tensioni caratteristiche peculiari. 

La formula dell'altezza di una sezione di trave in calcestruzzo è infatti la seguente:

                  h=( M/(r*fcd*b/2))^0,5

dove M è il momento massimo, fcd la tensione di progetto, che nel caso del calcestruzzo armato calcolo con la seguente:

                  fcd=fck*0,85/1,5 

mentre r è un valore adimensionale dato dalla seguente formula:

                  r =α*(1-(α/3))

e α, è un altro valore adimensionale dato da uno specifico rapporto tra le tensioni di progetto dei materiali componenti il c.a.

                  α= (fcd/E)/(fcd/E)+(fyd/E)

Conoscendo i seguenti valori, e imponendo una base, posso ricavare un'altezza per la mia sezione a cui dovrò aggiungere lo spessore del copriferro, e ingegnierizzando i valori avrò ottenuto il predimensionamento della trave.

5) Per il dimensionamento dei pilastri, si seguono gli stessi criteri di cui ci siamo serviti per predimensionare il pilastro in legno, quindi considereremo la resistenza sia a compressione, sia a presso/flessione. 

Considero quindi l'area minima necessaria ricavando lo sforzo N massimo, che trovo con la somma:

                    Nmax = ((qu*Ainf) + qt)* np

Dove qt è il peso delle travi, e np, il numero di piani del mio edificio.

Da qui trovo l'Area minima per resistere alla compressione 

Diverso è il caso, analogamente per il primo calcolo che abbiamo considerato per la struttura in legno, per determinare l'area necessaria, in funziona del momento di inerzia minimo della sua sezione, nel caso in cui consideriamo il pilastro flettersi per effetto della compressione di punta esercitato su di esso.

considero per ricavare il mio momento di inerzia necessario, il raggio minimo di inerzia, che desumo dalla formula:

                      ρmin=l0/λ

dove l0 è la lunghezza libera di inflessione, seguendo gli stessi ragionamenti per l'acciaio.

Posso allora ricavare λ dalla seguente formula:

                     λ=π *(E/fd)^0,5

I restanti dati, sono dati che conosco e che determino io.

conoscendo quindi il raggio minimo di inerzia, posso desumere la base, quindi il lato più corto del pilastro, necessario per raggiungere l'area interessata.

                     b=2*((3)^0,5)*ρmin

Ora posso trovare l'altro lato, mettendo in rapporto tra loro l'area trovata inizialmente e la base.

6) Una volta trovati su sap i momenti massimi reali, faccio la verifica tensionale, utilizzando le stesse formule usate per il dimensionamento del telaio in acciaio, e se le sezioni non sono verificate, le cambio fino ad ottenere un risultato corretto.

 

L’esercitazione prevede il dimensionamento delle travi di un telaio, considerando tre soluzioni tecnologiche diverse (in legno, acciaio e calcestruzzo armato). Il procedimento di progetto prevede di uguagliare la tensione massima (sigma max) presente nelle travi con la tensione di progetto (Fyd), definita dalla normativa  e tipica di ogni materiale.

Prendo in considerazione un generico piano di carpenteria di un edificio a telai piani. Disegno l’orditura del solaio, distinguendo le travi principali (vincolate ai pilastri attraverso appoggi semplici) e secondarie, e individuo la trave più sollecitata (ossia quella con l’aria d’influenza maggiore).

TELAIO

Per il dimensionamento di una struttura portante, che dipende dalle dimensioni dell’edificio, si fa fede in Italia alle NTC (Norme Tecniche di Costruzione) del 2008. La normativa prevede la progettazione della struttura portante, per la "vita utile" dell'edificio", in due stati:

- Stati Limite di Esercizio (SLE): sono associati ad una perdita di funzionalità dell’opera, ad esempio danneggiamenti locali di fessurazione. Lo SLE considera la struttura in fase elastica (fase in cui un corpo soggetto ad un’azione temporanea, mantiene la sua geometria senza deformarsi al termine dell’Azione).

- Stati Limite Ultimo (SLU): sono legati al collasso di un’intera opera oppure di una sua parte. Lo SLU considera la struttura in fase plastica (fase in cui un corpo soggetto ad una azione temporanea, al termine di essa rimane deformato, cambiando le sue proprietà meccaniche).

Il superamento dello stato limite ultimo genera il collasso della struttura e nel caso in esame la struttura portante verrà dimensionata allo SLU.

Nella figura sottostante è disegnata una struttura a telaio composta da un sistema di elementi verticali (pilastri) ed elementi orizzontali (travi) che successivamente verrà dimensionata nel  punto in cui la trave è più caricata con 3 materiali e tecniche costruttive diverse: Cemento Armato (CA), Acciaio e Legno.

I numeri rappresentano i singoli pilastri, il simbolo nella campata segna l’andamento dei travetti che scaricano il peso sulle travi principali che a loro volta scaricano il peso sull’esterno. La travi secondarie collegano le travi principali e collaborano alla stabilità della struttura. Le quote esterne ci permettono di calcolarci l’area d’influenza del probabile pilastro più sollecitato.

Procedo con il dimensionamento del pilastro 07 e della trave principale 03-11 che risentono di una maggiore area d’influenza di carico. Il dimensionamento di travi e pilastri verrà eseguito usando un modello semplificato di struttura.

Tramite l’analisi dei carichi si determina un’area di un metro quadro tipo di solaio. Moltiplicando l’area tipo di solaio per l’interasse della trave si ottiene il carico distribuito.

ANALISI DEI CARICHI

Prendo in considerazione tre tipologie differenti di solaio: solaio in latero-cemento, solaio in acciaio e solaio in legno.

La Normativa suddivide il solaio in tre differenti carichi: carico strutturale Gk1, carico permanente Gk2 e carico variabile Qk.

Lo SLU considera la possibilità che i carichi siano superiori a quelli effettivamente agenti e che le resistenze dei materiali siano inferiori a quelle considerate. Le resistenze sono determinate da prove sperimentali secondo un metodo probabilistico, quindi non avendo sempre la certezza che il materiale si comporti allo stesso modo, vengono introdotti dei coefficienti di sicurezza che amplificano il carico e dei coefficienti che riduco le resistenze. Seguendo le tabelle della normativa il carco ultimo risulta Qu= γg1*Gk1 + γg2*Gk2 + γqi*Qk  dove Gk1 è il carico strutturale (peso proprio della struttura), Gk2 è il carico permanente non strutturale (carico degli elementi non strutturali), e Qk sono i carichi variabili, dettati nella Tabella 3.1.II delle NTC 2008.

CEMENTO ARMATO trave

Prendiamo in considerazione 1 mq di solaio in latero-cemento. La figura mostra una sezione perpendicolare all'orditura dei travetti di cemento armato per mostrare i singoli materiali. Il carico ultimo che se ne ricava è uguale a Qu= 10,7 KN/m^2

Per il dimensionamento della trave è stato utilizzato un foglio elettronico che ci permette di ricavare l’altezza utile della sezione. Essendo il cemento un materiale che resiste bene a compressione e quasi niente a trazione ha bisogno dell’aiuto dell’acciaio per colmare questo gap. Il Cls e l’Acciaio hanno un comportamento meccanico diverso ma la deformazione deve essere la stessa per via del fattore di omogeneizzazione. Dato che i moduli elastici sono differenti viene introdotto questo coefficiente definito come il rapporto tra i moduli elastici dei due materiali. Dato che con il tempo il Cls abbassa la rigidezza per effetto della viscosità si accorcia e quindi n=15.

Tralasciando la dimostrazione diamo per buono che l’altezza utile della sezione è la radice quadrata del momento fratto una la base e diversi coefficienti.

Inserendo i dati relativi:

-alle geometrie del telaio (La;Lb;luce)

-ai risultanti dell’analisi dei carichi (qs;qp;qa; con qu=luce*10,7)

-al momento massimo in mezzeria pari a ql^2/8

-a dei valori che troviamo (fyk;fyd;fcd;Es;Ec) e scegliamo (fck) in linea di massima dalla normativa

Troviamo un’altezza utile di 428mm, considerando un copriferro di 40 mm per coprire le barre d'acciaio risulta necessaria una trave principale alta almeno 468mm.
Per una facilità di realizzazione della trave, la sezione viene ingegnerizzata, quindi verrà utilizzata una trave con un’altezza pari a 500mm.
 

ACCIAO trave

Prendiamo in considerazione 1 mq di solaio con lamiera grecata che moltiplicato per la luce e l'interasse della Trave Principale ci darà il carico dell'Area di influenza (qu). La figura mostra una sezione perpendicolare all'orditura della lamiera grecata il carico ultimo ricavato è Qu= 12,25 KN/m^2

Anche per il dimensionamento della trave d’acciaio è stato utilizzato un foglio elettronico, ma stavolta non dobbiamo ricavarci l’altezza utile ma il procedimento è più veloce. Si considera al posto della tensione σ(y) la resistenza di progetto (Fyd) che serve per ricavarci attraverso il rapporto tra Momento massimo (ql^/8) e Fyd stesso il modulo di resistenza a flessione Wpl. Esso è il rapporto tra Mmax e Fyd, ma bisogna stare attenti alle equivalenze. Trovato il valore minimo Wpl=316,5 cm^3 della trave si prende il sagomario delle Ipe e si ricerca il valore Wx che supera quello trovato.

Dalla tabella si sceglie un’IPE 240 con Wx=366,65cm^3.

 

LEGNO trave

Come nei casi precedenti prendiamo in considerazione 1mq di solaio ma in legno. La figura mostra una sezione perpendicolare all’orditura dei travetti in legno ed il carico ultimo risultante è Qu= 7,6 KN/m^2

Ricorrendo sempre al foglio elettronico per il dimensionamento della trave il procedimento è simile a quello utilizzato per la trave in acciaio. Si parte dalla formula di Navier dove la tensione σ(y) è il rapporto tra il Momento Massimo (Mmax) e il modulo di resistenza a flessione (Wx). Da questa formula si ricava la Wx=3441cm^3 e poi si trova facilmente l’altezza utile della sezione facendo la radice quadrata del rapporto tra 6Wx e la base sapendo che il modulo di resistenza a flessione per una sezione rettangolare è Wx=bh^2/6. I valori non ancora citati(Fc0,k;kmod,γ) si ricavano dalla normativa.

Il risultato ottenuto mostra che l'altezza minima devo essere di 35,9 cm, che ingegnerizzato da un'altezza della trave di 40 cm.

PILASTRI

Nella costruzione del telaio, dopo aver determinato l’altezza della trave più sollecitata si dimensionano i pilastri. Per semplificare considero soltanto l’area d’influenza segnalata, ma per un dimensionamento più accurato dovrei dimensionare anche le altre campate. In ogni caso basterebbe aggiungere i dati ai fogli excel che li calcolerebbero automaticamente. Dunque così come nella trave si prende in esame l’area d’influenza maggiore (ricavata dividendo a metà le luci delle campate più grandi) che risente del maggior carico.

La sollecitazione principale a cui è sottoposto il pilastro è lo sforzo normale, ma nel nostro caso considereremo anche la flessione dovuta alle forze che esercita il vento sulle facciate.
Per dimensionare il pilastro bisogna verificare che lo sforzo normale non superi la resistenza del materiale.
Prendendo in esempio il modello di trave di Eulero-Bernoulli la relazione del legame costitutivo è σ = N/A.
Per ottenere l'area minima, sostituisco alla tensione σ la resistenza del materiale ( ovvero la resistenza caratteristica fk se sto progettando allo Stato Limite di Esercizio altrimenti la resistenza di progetto fd  per lo Stato Limite Ultimo).

Il problema principale dei pilastri è la possibilità per elementi snelli di potersi inflettere,  per questo bisogna verificare l’instabilità. L'acciaio è il materiale che tra i tre proposti ha la resistenza più alta e permette di avere elementi molto snelli. Più è snello un elemento più risente dell’instabilità. L'elemento snello sottoposto a un carico verticale può inflettersi in diversi modi a seconda della condizioni ai bordi del pilastro (vincoli). La snellezza viene definita come il rapporto tra la luce libera di inflessione (distanza tra due flessi della deformata) e il raggio di inerzia minimo (definisce come le componenti di un oggetto sono distribuite attorno al suo asse di rotazione). Avendo scelto una struttura isostatica con cerniera e carrello come attacco a terra, dalla normativa troviamo che β=1.

CEMENTO ARMATO

Per progettare e verificare i pilastri si utilizza nuovamente excel, questa volta si creano 6 fogli relativi allo sforzo Normale e al dimensionamento per ogni tipologia costruttiva. Il procedimento per trovare la Nmax dipende dal numero di piani (n) e lo sforzo Normale relativo ad ogni piano (che si ottiene dal prodotto dell’area d’influenza (Ainf) per il peso delle travi espresso in KN per il carico ultimo (qu) derivante dall’analisi dei carichi). Trovato Nmax=359,5KN si riporta nella tabella relativa al dimensionamento. Anche qui, l’obiettivo è raggiungere la base e l’altezza di design per passare poi alla verifica della struttura. Dai fogli elettronici risulta che il pilastro al piano terra deve avere un’area minima di 264cm^2 e di conseguenza la base (ricavata moltiplicando ρmin*radice di 12) e l’altezza devono essere superiori rispettivamente a 8,4cm e 31,4cm. Scelgo un pilastro avente base e altezza uguali pari a 35cm evitando i problemi di inflessione poiché l’Area di design= 1225cm^2 supera l’Area minima=264cm^2.

ACCIAIO

Per il dimensionamento dei pilastri in acciaio utilizzo i profili HE in quanto più tozzi ed adatti di quelli IPE usati per la trave. Come per il Cemento Armato trovo lo Sforzo Normale Massimo=542,2KN che mi serve per trovare la geometria del pilastro. Essendo molto simile il procedimento, anche se nell’acciaio come detto in precedenza va considerato che avendo sezioni snelle c’è rischio di instabilità, mi limito a dire che nei fogli elettronici rispetto al c.a. cambiano i valori delle resistenze del materiale e per scegliere il profilato dal sagomario ho bisogno di trovare un’Inerzia minima che si ricava Imin=ρmin^2*Amin=235cm^4.

La resistenza molto elevata dell’acciaio permette di utilizzare un HEA140 che ha ovviamente un’inerzia maggiore di quella minima; inoltre per l’instabilità è verificato che λ<λc.

LEGNO

Il dimensionamento del legno ha lo stesso procedimento dell’acciaio in quanto anch’esso ha delle sezioni molto snelle. La Nmax=235,5KN è più bassa rispetto alle altre perché chiaramente il legno è un materiale che peso molto meno degli altri due 6KN/m^3 e addirittura pesa anche meno dell’acqua. Dalla tabella si evince chiaramente che il procedimento e simile e la sezione verificata viene di 15cmX15cm.

Dopo aver eseguito il predimensionamento della struttura si crea il tealio su SAP2000 dove si inseriscono per ogni tipologia costruttiva utilizzata i carichi linearmente distribuiti Qu al fine di ricavarci i diagrammi delle sollecitazioni e quindi i punti in cui sono massimi lo sforzo Normale e il Momento. Ottenuti questi valori si passa alla verifica a presso-flessione perché va considerata anche la pressione che il vento esercita sulle facciate. 
 

 

 

 

 

 

 

 

 

Il progetto proposto ha una destinazione d’uso di tipo residenziale ed è composto da 6 piani con il medesimo schema strutturale.
Considerando come dati di progetto la pianta e la sezione della nostra struttura, progetteremo tre differenti solai da associare al progetto dimensionale di travi e pilastri in tre differenti tecnologie costruttive: calcestruzzo armato, acciaio e legno.
Per prima cosa analizziamo la pianta, individuando le travi e i pilastri evidenziati nel disegno. Per ognuna delle tecnologie costruttive procederemo con l’analisi dei carichi agenti sul solaio, che si dividono in carichi strutturali (q_s), carichi permanenti (q_p) e carichi accidentali (q_a).

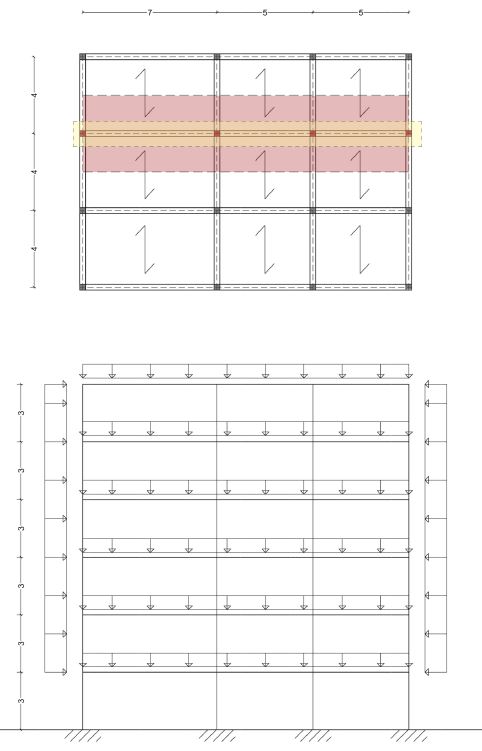
SOLAIO IN CLS ARMATO

Dimensionamento travi

E’ stato scelto un solaio in latero cemento. Di seguito è rappresentato graficamente, completo di tutte le sue parti costruttive.

 

 

 

 

 

 

 

 

 

 

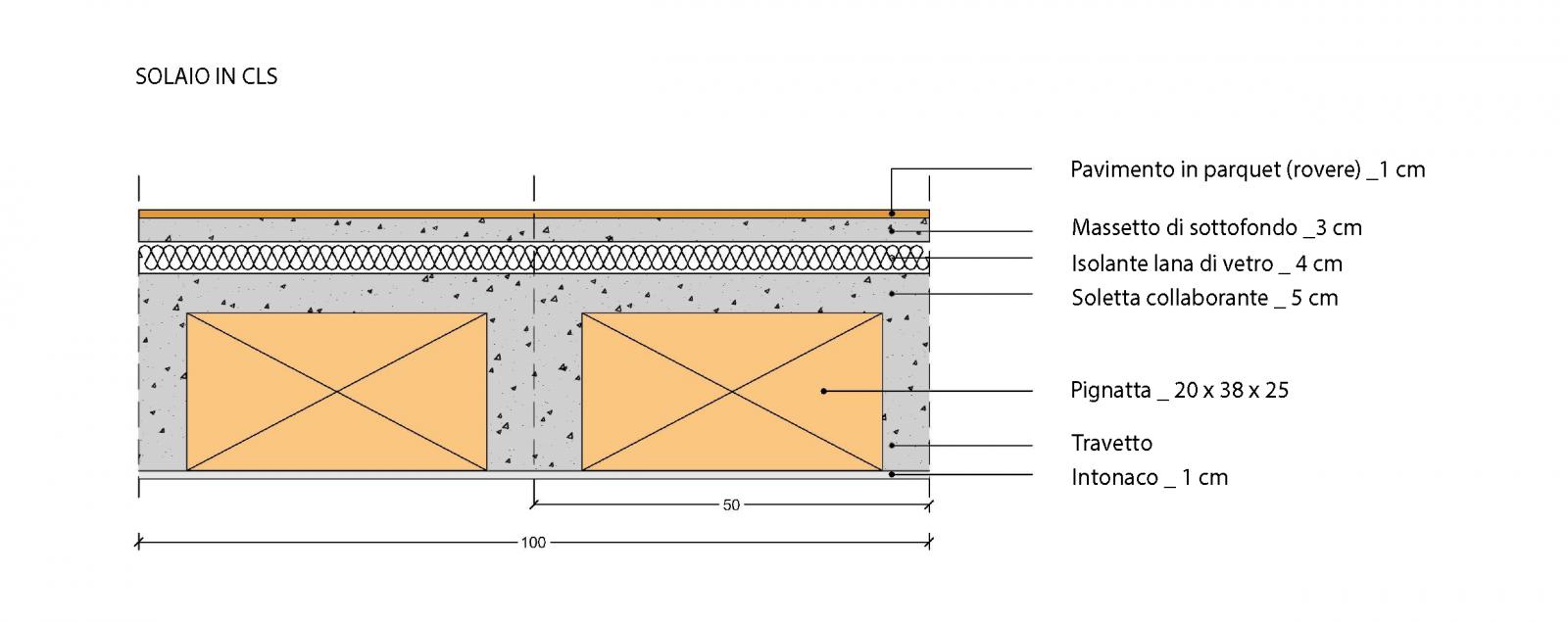
Conoscendo la stratigrafia del solaio, possiamo ricavare il volume e il peso al metro quadro di ciascun componente. 

Carico strutturale q_s:

• Travetti in cls:

Dimensioni: (12 x 20) cm
Peso specifico: 25 KN/m³
Volume: (0,12 x 0,20 x 1) m x 2 = 0,048 m³
Peso al metro quadro: 0,048 m³/m² x 25 KN/m³ = 1,2 KN/m²

• Soletta in cls (Caldana):

Dimensioni: 5 cm
Peso specifico: 25 KN/m³
Volume: (0,05 x 1 x 1) m = 0,05 m³
Peso al metro quadro: 0,05 m³/m² x 25 KN/m³ = 1,25 KN/m²

• Pignatte:

Dimensioni: (20 x 38 x 25) cm
Peso specifico: 9,8 Kg
Peso al metro quadro: 9,8 Kg x 8 1/m² = 0,784 KN/m²

 

q_s = (1,2+1,25+0,784) KN/ m2 = 3,23 KN/m²

 

Carico permanente q_p:

• Pavimentazione in parquet:

Spessore: 1 cm
Peso specifico: 7,2 KN/m³
Volume: (0,01 x 1 x 1) m =0,01 m³
Peso al metro quadro: 0,01 m³/m² x 7,2 KN/m³ = 0,072 KN/m²

• Massetto di sottofondo:

Spessore: 3 cm
Peso specifico: 20 KN/m²
Volume: (0,03 x 1 x 1) m = 0,03 m³
Peso al metro quadro: 0,03 m³/m² x 20 KN/m² = 0,6 KN/m²

• Isolante in lana di vetro:

Spessore: 4 cm
Peso specifico: 0,2 KN/m³
Volume: (0,04 x 1 x 1) m = 0,034 m³
Peso al metro quadro: 0,04 m³/m² x 0,2 KN/m² = 0,08 KN/m²

• Intonaco:

Spessore: 1 cm
Peso specifico: 18 KN/m²
Volume: (0,01 x 1 x 1) m = 0,01 m³
Peso al metro quadro: 0,01 m³/m² x 18 KN/m² = 0,18 KN/m²

Il peso va incrementato con due coefficienti, definiti dalla normativa:

• Incidenza impianti: 0,5 KN/m²
• Incidenza tramezzi: 1,0 KN/m²

 

q_p = (0,072+0,6+0,008+0,18+0,5+1) KN/ m2 = 2,36 KN/m²

 

Carico accidentale q_a:

Questo valore varia in base alla destinazione d’uso dell’edificio che, in questo caso, è residenziale.

q_a = 2 KN/m²

Avendo inserito nella tabella Excel tutti i valori trovati, possiamo procedere con il calcolo di q_u, il carico allo stato limite ultimo, sommando q_s, q_p e q_a, aumentati ciascuno del loro coefficiente di sicurezza Ɣ_G1, Ɣ_G2, Ɣ_Q1(rispettivamente pari a 1,3 – 1,5 – 1,5). Adesso, per trovare il valore del carico lineare incidente sulla trave, basta moltiplicare il risultato per l’interasse i (nel nostro caso 4 m):

q_u = (Ɣ_G1 x q_s + Ɣ_G2 x q_p + Ɣ_Q1 x q_a) x Interasse = (3,23 x 1,3 + 2,36 x 1,5 + 2 x 1,5) KN/m² x 4 m = 42,46 KN/m

 

 

A questo punto possiamo passare al calcolo del momento flettente massimo agente sulla trave. Essendo una trave doppiamente appoggiata, la formula è nota come: M_max = ql²/8

M_max = [42,46 KN/m x (7 m)²]/8 = 263,11 KNm

Ora scegliamo il tipo di calcestruzzo e di acciaio che vogliamo utilizzare per sviluppare il nostro progetto, ricavando la loro tensione di progetto:

Acciaio:

F_yd = f_yk/Ɣ_s

Dove:
F_yk: Tensione caratteristica di snervamento dell’acciaio, che risulta, da normativa, pari a 450 N/mm² per quanto riguarda gli acciai da armatura.
Ɣ_s: Coefficiente parziale di sicurezza pari a 1,15.

Quindi avremo: F_yd = 450 N/mm² / 1,15 = 391,30 N/mm²

Calcestruzzo:

F_cd = α_cc x (f_ck/Ɣ_c)

Dove:
α_cc: Coefficiente riduttivo per le resistenze di lunga durata, pari a 0,85
f_ck: Resistenza caratteristica a compressione del cls, data dal tipo di cls scelto. In questo caso sarà 50 N/mm²
Ɣ_c: Coefficiente parziale di sicurezza pari a 1,5 per il cls.

Quindi avremo: F_cd = 0,85 x (50 N/mm² / 1,5) = 28,33 N/mm²

 

 

Definendo arbitrariamente la base della sezione, noti i valori delle tensioni di progetto, calcoliamo h_u, l'altezza utile della sezione, la cui formula risulta essere:

h_u = r √ (M_max/b) = 41,55 cm

Sommando a questo valore, quello dell'altezza del copriferro δ (5 cm), è possibile ottenere h_min:

h_min = h_u + δ = (41,55 + 5) cm = 45,55 cm 

Tale valore viene ingegnerizzato, portano l'altezza alla decima immediatamente superiore al valore minimo ottenuto: 
H = 50 cm

Il foglio di calcolo excel, a questo punto, individua quale sia il peso proprio della trave appena determinata.

 

 

Terminata la fase di progetto, si passa alla fase di verifica. Andremo adesso ad aggiungere il peso proprio della trave alla somma dei carichi portati dalla trave stessa, calcoleremo il momento massimo e verificheremo se la sezione scelta sarà adatta anche a queste nuove caratteristiche di carico. 

Peso unitario = 3,13 KN/m viene moltiplicato per Ɣ_G1 = 1,3 ed il nuovo carico diventerà:

q'_u = q_u + (3,13 KN/m x 1,3) = 42,46 KN/m + 4,069 KN/m = 47,02 KN/m

Sostituendo questo nuovo valore per i calcoli successivi, verrà che:

M'_max = [47,02 KN/m x (7 m)²]/8 = 287,99 KNm

h'_u = 43,47 cm

h_min = (43,47 + 5) cm = 47,47 cm   Quindi: H = 50 cm

La sezione scelta è verificata in quanto H' < H

 

 

 

Gli stessi passaggi vengono seguiti per le altre luci (entrambe di 5 m) e si avranno i seguenti risultati:

 

 

 

 

 

 

 

Inserimento della struttura in SAP

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

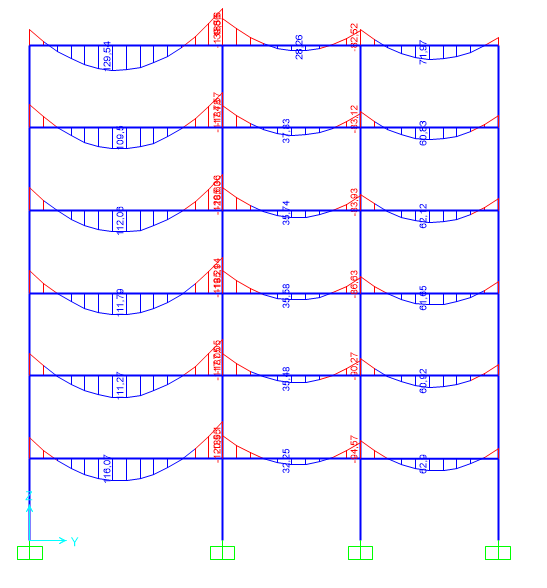
Verifica

Una volta individuato su SAP il momento flettente massimo della trave maggiormente sollecitata, lo riportiamo sul file di calcolo per verificare che questo sia minore di M_max trovato nei nostri calcoli precedenti. 

 

 

 

 

 

 

 

Dimensionamento pilastri

Dopo aver individuato i pilastri maggiormente sollecitati, attraverso il file excel, inserisco i dati. Quelli iniziali da cui partire sono, innanzitutto, L₁ e L₂, i due lati dell'area di influenza del pilastro in esame. Ottengo, così, il valore dell'area di influenza (il cui peso è portato dal pilastro). Partendo dal pilastro A, si avrà:

 

 

 

Avendo il valore dell'area della trave, precedentemente calcolata, e del peso specifico del materiale considerato, è possibile ottenere il peso della trave stessa:

 

 

 

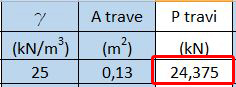
Riprendendo i risultati precedenti, individuiamo q_u, sommando q_s, q_p, q_a aumentati ciascuno del loro coefficiente di sicurezza Ɣ_G1, Ɣ_G2, Ɣ_Q1:

q_u = (Ɣ_G1 x q_s + Ɣ_G2 x q_p + Ɣ_Q1 x q_a) = (3,23 x 1,3 + 2,36 x 1,5 + 2 x 1,5) KN/m² = 10,739 KN/m²

Riusciamo, così, ad individuare lo sforzo normale di un solo piano agente sul pilastro:

N = (q_u x A_inf) + P_travi = 10,739 KN/m x 14 m² + 24,375 KN = 174,721 KN

Considerando il nostro edificio costituito da 6 piani, avremo: 

N_max = N x Num_piani = 174,721 KN x 6 = 1048,33 KN

 

 

 

Per i pilastri B, C, D verranno seguiti gli stessi passaggi:

 

 

 

 

 

Procediamo ora con il predimensionamento della sezione del pilastro, a partire dalla resistenza caratteristica del cls, trovando la sua tensione di progetto e l'area minima necessaria alla sezione affinchè il materiale non giunga a rottura:

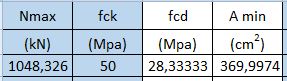
f_ck = 50 MPa
f_cd = 0,85 x (50 MPa / 1,5) = 28,33 MPa
A_min = N_max / f_cd = 1048,33 KN / 28,33 MPa x 10 = 369,99 cm²

 

 

 

Considerando alcuni dati, quali: 
E = modulo elastico in percentile = 21000 MPa
I = altezza del pilastro = 3 m
β = influenza dei vincoli = 1 nel caso del doppio incastro

Si ricavano: 

Valore della snellezza: λ =  π x √(E/f_cd) = π x √ (21000 MPa / 28,33 MPa) = 85,52 

 ρ_min = (β x l) / λ = (1 x 3 m) / 85,52 x 100 = 3,50 cm

Sapendo che per i pilastri in cemento armato ρ_min = √ (1/12) x b , con la formula inversa si può trovare una delle dimensioni della sezione:

b_min = ρ_min x √ 12 = 3,50 cm x 3,46 = 12,15 cm

L'altra dimensione della sezione si ottiene dividendo l'area per la base trovata:

h_min = A_min / b = 369,99 cm²  / 12,15 cm = 30,45 cm

Tali risultati vanno ingegnerizzati, diventando:
b_design = 25 cm
h_design = 45 cm

 

 

 

Per i pilastri B, C, D verranno seguiti gli stessi passaggi:

 

 

 

 

 

Inserimento della struttura in SAP

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

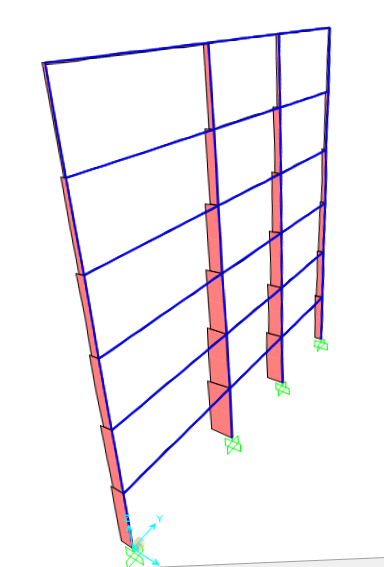
Verifica

Una volta individuato su SAP il momento flettente massimo e lo sforzo normale del pilastro maggiormente sollecitato, lo riportiamo sul file di calcolo, utilizzando la formula di verifica a pressoflessione. Quindi avremo:

W_max = modulo di resistenza a flessione = b_design x h_design² / 6 = (25 cm x 2025 cm² ) / 6 = 8437,50 cm³

Da qui troviamo la Tensione massima (sigma) = (N/A) + (M/W_max) = (836 KN / 1125 cm²) x (10) + (47 KNm / 8437,50 cm³) = 13,00 MPa

Tensione massima < f_cd  ----> verificata.

 

 

 

 

 

SOLAIO IN ACCIAIO

Per questo tipo di tecnologia è stato scelto un solaio in lamiera grecata. Di seguito è rappresentato graficamente, completo di tutte le sue parti costruttive.

 

 

 

 

 

 

 

 

 

 

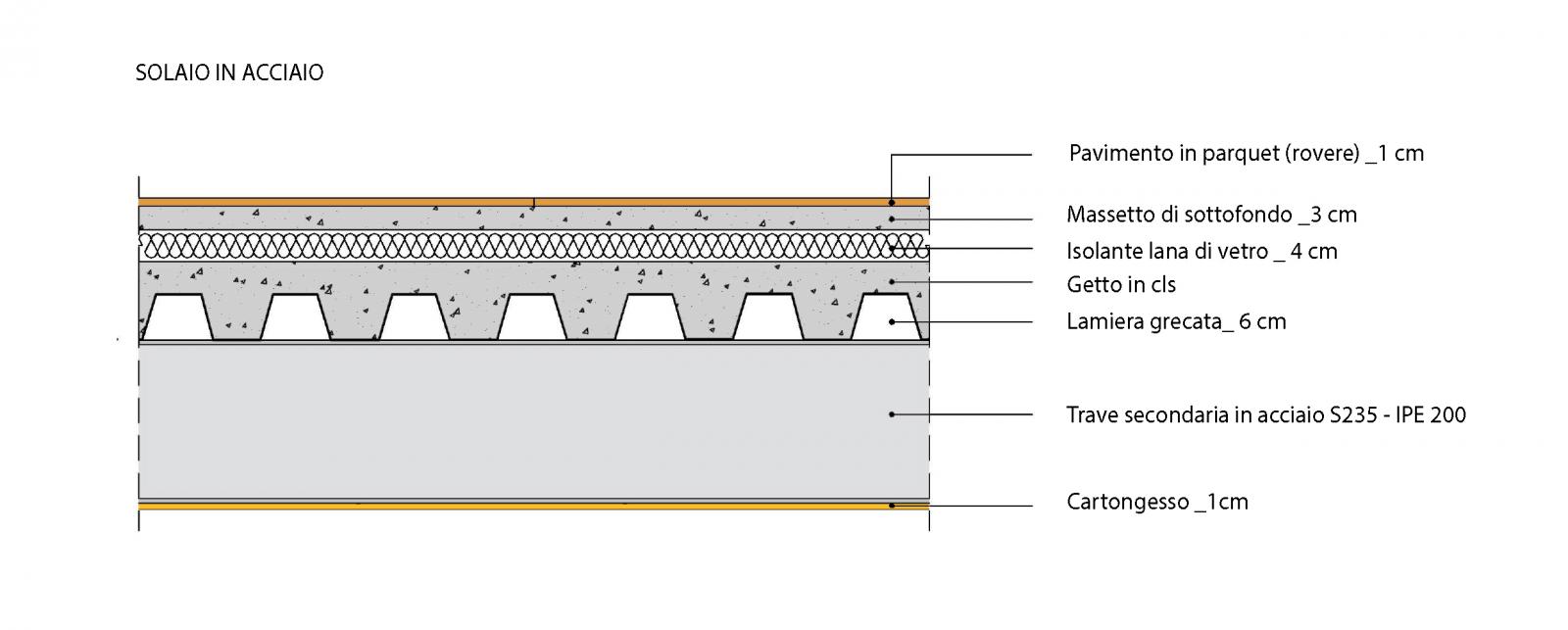
Dimensionamento travi

Carico strutturale q_s:

• Travetti IPE 200 in acciaio S235:

Area: 28,48 cm² = 0,0028 m²
Peso: 22,4 Kg/m = 0,224 KN/m
Peso al metro quadro: 0,224 KN/m²

• Soletta in cls (Caldana):

Area: 0,07 m²
Peso specifico: 25 KN/m³
Volume: (0,07 x 1 x 1) m = 0,07 m³
Peso al metro quadro: 0,07 m³/m² x 25 KN/m³ = 1,75 KN/m²

 

q_s = (0,0024 + 1,75) KN/ m2 = 1,97 KN/m²

 

Carico permanente q_p:

• Pavimentazione in parquet:

Spessore: 1 cm
Peso specifico: 7,2 KN/m³
Volume: (0,01 x 1 x 1) m =0,01 m³
Peso al metro quadro: 0,01 m³/m² x 7,2 KN/m³ = 0,072 KN/m²

• Massetto di sottofondo:

Spessore: 3 cm
Peso specifico: 20 KN/m²
Volume: (0,03 x 1 x 1) m = 0,03 m³
Peso al metro quadro: 0,03 m³/m² x 20 KN/m² = 0,6 KN/m²

• Isolante in lana di vetro:

Spessore: 4 cm
Peso specifico: 0,2 KN/m³
Volume: (0,04 x 1 x 1) m = 0,034 m³
Peso al metro quadro: 0,04 m³/m² x 0,2 KN/m² = 0,08 KN/m²

• Cartongesso: 

Spessore: 1 cm
Peso specifico: 9 KN/m³
Volume: (0,01 x 1 x 1) m = 0,01 m³
Peso al metro quadro: 0,09 KN/m²

• Intonaco:

Spessore: 1 cm
Peso specifico: 18 KN/m²
Volume: (0,01 x 1 x 1) m = 0,01 m³
Peso al metro quadro: 0,01 m³/m² x 18 KN/m² = 0,18 KN/m²

• Incidenza impianti: 0,5 KN/m²
• Incidenza tramezzi: 1,0 KN/m²

q_p = (0,072+0,6+0,008+0,18+0,09+0,5+1) KN/ m2 = 2,45 KN/m²

 

Carico accidentale q_a:

Questo valore varia in base alla destinazione d’uso dell’edificio che, in questo caso, è residenziale.

q_a = 2 KN/m²

q_u = (Ɣ_G1 x q_s + Ɣ_G2 x q_p + Ɣ_Q1 x q_a) x Interasse = (1,97 x 1,3 + 2,45 x 1,5 + 2 x 1,5) KN/m² x 4 m = 36,94 KN/m

 

 

A questo punto possiamo passare al calcolo del momento flettente massimo agente sulla trave. Essendo una trave doppiamente appoggiata, la formula è nota come: M_max = ql²/8

M_max = [36,94 KN/m x (7 m)²]/8 = 226,28 KNm

Ora scegliamo il tipo di acciaio che vogliamo utilizzare per sviluppare il nostro progetto, ricavando la sua tensione di progetto:

F_d = f_yk/Ɣ_s

Dove:
F_yk: Tensione caratteristica di snervamento dell’acciaio, che risulta, da normativa, pari a 235 N/mm² per quanto riguarda l'acciaio scelto.
Ɣ_s: Coefficiente parziale di sicurezza pari a 1,05.

Quindi avremo: F_d = 235 N/mm² / 1,05 = 223,81 N/mm²

 

 

Calcolata la tensione di progetto, applichiamo la formula di Navier per ricavare il modulo di resistenza a flessione, per sapere quale sia il valore minimo che la nostra sezione può avere:

W_x,min = M_max/f_d = 226,28 KNm / 223,81 N/mm² x 1000 = 1011,05 cm³

Avendo utilizzato nei calcoli il valore di resistenza massima a flessione, sceglieremo nel profilario la sezione IPE con un valore W_x subito maggiore di quello da noi trovato. 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

In questo caso una trave IPE 400 con W_x = 1156,00 cm³

Gli stessi passaggi vengono seguiti per le altre luci (entrambe di 5 m) e si avranno i seguenti risultati:

 

 

 

 

Inserimento della struttura in SAP

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

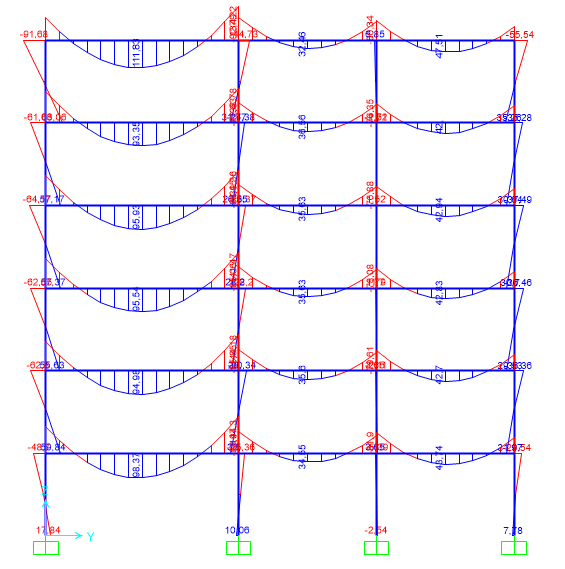
Verifica

Una volta individuato su SAP il momento flettente massimo della trave maggiormente sollecitata, lo riportiamo sul file di calcolo per verificare che questo sia minore di M_max trovato nei nostri calcoli precedenti. 

 

 

 

Dimensionamento pilastri

Ripeto quanto già fatto nel caso del cemento armato, partendo da L₁ e L₂, i due lati dell'area di influenza del pilastro in esame. Ottengo, così, il valore dell'area di influenza (il cui peso è portato dal pilastro). Partendo dal pilastro A, si avrà:

 

 

 

Individuiamo q_u:

q_u = (1,97 x 1,3 + 2,45 x 1,5 + 2 x 1,5) KN/m² = 9,236 KN/m²

Riusciamo, così, ad individuare lo sforzo normale di un solo piano agente sul pilastro:

N = (q_u x A_inf) + P_travi =9,236 KN/m x 14 m² + 4,97 KN = 134,27 KN

Quindi, avremo: 

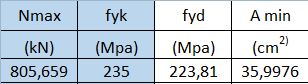
N_max = N x Num_piani = 134,27 KN x 6 = 805,65 KN

 

 

 

Per i pilastri B, C, D verranno seguiti gli stessi passaggi:

 

 

 

 

 

 

Procediamo ora con il predimensionamento della sezione del pilastro, avendo come dato:

f_yk = tensione di snervamento caratteristica = 235 MPa

Trovando:

f_yd = f_yk / Ɣ_s = 235 MPa / 1,05 = 223,81 MPa
A_min = N_max / f_yd = 805,65 KN / 223,81 MPa x 10 = 35,99 cm²

 

 

 

Considerando: 
E = 21000 MPa
I = 3 m
β = 1 

Si ricavano: 

λ = π x √ (21000 MPa / 223,81 MPa) = 96,23 

 ρ_min = (1 x 3 m) / 96,23 x 100 = 3,117 cm

Attraverso la abella dei profili HEA, ricavo i valori di A_design, I_design e ρ_min maggiori di quelli minimi ottenuti:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Il profilo individuato è un HEA160.

Per i pilastri B, C, D verranno seguiti gli stessi passaggi:

 

 

 

 

 

Inserimento della struttura in SAP

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

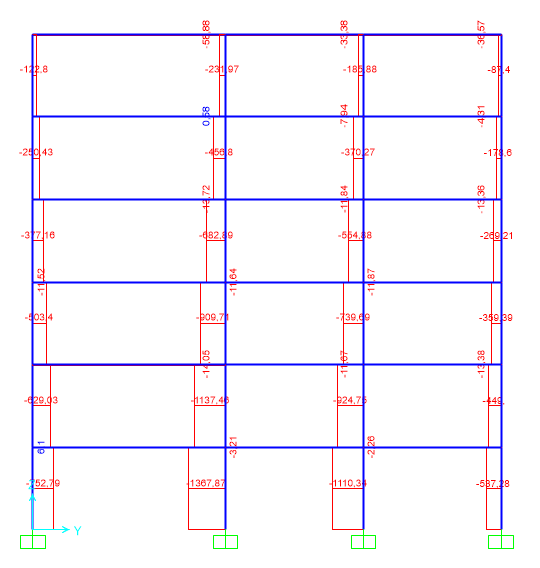
Verifica

Una volta individuato su SAP il momento flettente massimo e lo sforzo normale del pilastro maggiormente sollecitato, lo riportiamo sul file di calcolo, utilizzando la formula di verifica a pressoflessione. Quindi avremo:

Tensione massima (sigma) = (N/A) + (M/W_max) = (752 KN / 76,84 cm²) x (10) + (48,7 KNm / 675,10 cm³) = 170,003 MPa

N.B. La sezione dei pilastri risultano verificate a pressoflessione, modificandole rispetto alle ipotesi di progetto iniziali:

 

 

 

 

 

 

SOLAIO IN LEGNO

E’ stato scelto un solaio in legno con pannelli osb. Di seguito è rappresentato graficamente, completo di tutte le sue parti costruttive.

 

 

 

 

 

 

 

 

 

 

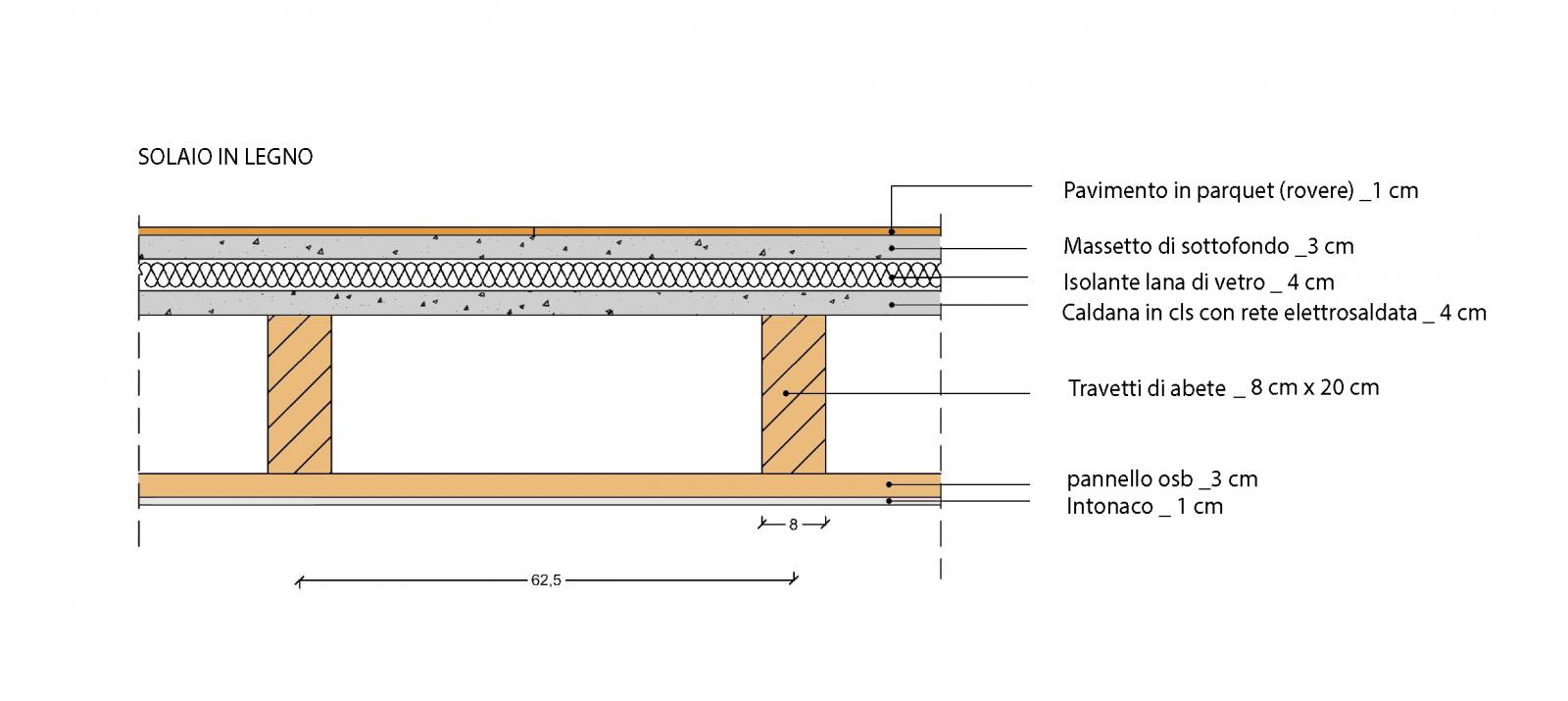
Carico strutturale q_s:

• Pannello OSB:

Spessore: 3 cm
Peso specifico: 6,5 KN/m³
Volume: (0,03 x 1 x 1) m = 0,03 m³
Peso al metro quadro: 0,03 m³/m² x 6,5 KN/m³ = 0,195 KN/m²

• Travetto in legno lamellare di abete:

Dimensioni: (8 x 20) cm
Peso specifico: 5,50 KN/m³
Volume: (0,08 x 0,2 x 1) m = 0,016 m³ --> 0,016 x (1/62,5) = 0,000256 m³
Peso al metro quadro: 0,000256 m³/m² x 5,50 KN/m³ = 0,0014 KN/m²

 

q_s = (0,195 KN/m² x 2) +0,0014 KN/ m2 = 0,39 KN/m²

 

Carico permanente q_p:

• Pavimentazione in parquet:

Spessore: 1 cm
Peso specifico: 7,2 KN/m³
Volume: (0,01 x 1 x 1) m =0,01 m³
Peso al metro quadro: 0,01 m³/m² x 7,2 KN/m³ = 0,072 KN/m²

• Massetto di sottofondo:

Spessore: 3 cm
Peso specifico: 20 KN/m²
Volume: (0,03 x 1 x 1) m = 0,03 m³
Peso al metro quadro: 0,03 m³/m² x 20 KN/m² = 0,6 KN/m²

• Isolante in lana di vetro:

Spessore: 4 cm
Peso specifico: 0,2 KN/m³
Volume: (0,04 x 1 x 1) m = 0,034 m³
Peso al metro quadro: 0,04 m³/m² x 0,2 KN/m² = 0,008 KN/m²

• Caldana in cls con rete elettrosaldata:

Spessore: 4 cm
Peso specifico: 25 KN/m²
Volume: (0,04 x 1 x 1) m = 0,04 m³
Peso al metro quadro: 0,04 m³/m² x 25 KN/m² = 1 KN/m²

• Intonaco:

Spessore: 1 cm
Peso specifico: 18 KN/m²
Volume: (0,01 x 1 x 1) m = 0,01 m³
Peso al metro quadro: 0,01 m³/m² x 18 KN/m² = 0,18 KN/m²

Il peso va incrementato con due coefficienti, definiti dalla normativa:

• Incidenza impianti: 0,5 KN/m²
• Incidenza tramezzi: 1,0 KN/m²

 

q_p = (0,072+0,6+0,008+1+0,18+0,5+1) KN/ m² = 3,36 KN/m²

 

Carico accidentale q_a:

Questo valore varia in base alla destinazione d’uso dell’edificio che, in questo caso, è residenziale.

q_a = 2 KN/m²

Avendo inserito nella tabella Excel tutti i valori trovati, possiamo procedere con il calcolo di q_u, il carico allo stato limite ultimo, sommando q_s, q_p e q_a, aumentati ciascuno del loro coefficiente di sicurezza Ɣ_G1, Ɣ_G2, Ɣ_Q1(rispettivamente pari a 1,3 – 1,5 – 1,5). Adesso, per trovare il valore del carico lineare incidente sulla trave, basta moltiplicare il risultato per l’interasse i (nel nostro caso 4 m):

q_u = (Ɣ_G1 x q_s + Ɣ_G2 x q_p + Ɣ_Q1 x q_a) x Interasse = (0,39 x 1,3 + 3,36 x 1,5 + 2 x 1,5) KN/m² x 4 m = 34,19 KN/m

 

A questo punto possiamo passare al calcolo del momento flettente massimo agente sulla trave. Essendo una trave doppiamente appoggiata, la formula è nota come: M_max = ql²/8

M_max = [34,19 KN/m x (7 m)²]/8 = 209,40 KNm

Procediamo inserendo il valore di f_mk, la resistenza caratteristica a flessione del legno prescelto: nel nostro caso utilizziamo il valore del legno lamellare. 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Lo stesso facciamo per K_mod, il coefficiente diminutivo dei valori di resistenza del materiale. E' definito dalla normativa e tiene conto dell'effetto della durata del carico e delle condizioni in cui la struttura si andrà ad inserire:

 

 

 

 

 

 

 

 

 

 

 

 

Troviamo, inoltre, il coefficiente parziale di sicurezza del legno lamellare Ɣ_m:

 

 

 

 

 

 

 

 

I tre valori, combinati, ci permettono di ricavare la tensione di progetto, secondo la formula:

f_d = (K_mod x f_mk) / Ɣ_m

 

 

Definendo arbitrariamente la base della sezione (nel nostro caso 26 cm), calcoliamo h_min, l'altezza minima della sezione, la cui formula risulta essere:

h_min = √ [(6 x M_max x 1000) / (b x f_d)] = 56,96 cm

Tale valore viene ingegnerizzato, portano l'altezza alla decima immediatamente superiore al valore minimo ottenuto: 
H = 60 cm

 

 

La trave adottata avrà dimensioni 26 x 60 cm

Gli stessi passaggi vengono seguiti per le altre luci (entrambe di 5 m) e si avranno i seguenti risultati:

 

 

 

Inserimento della struttura in SAP

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Verifica

Una volta individuato su SAP il momento flettente massimo della trave maggiormente sollecitata, lo riportiamo sul file di calcolo per verificare che questo sia minore di M_max trovato nei nostri calcoli precedenti. 

 

 

Dimensionamento pilastri

Ripeto quanto già fatto nei casi precedenti, partendo da L₁ e L₂, i due lati dell'area di influenza del pilastro in esame. Ottengo, così, il valore dell'area di influenza (il cui peso è portato dal pilastro). Partendo dal pilastro A, si avrà:

 

 

Individuiamo q_u:

q_u = (0,39 x 1,3 + 3,36 x 1,5 + 2 x 1,5) KN/m² = 8,54 KN/m²

Riusciamo, così, ad individuare lo sforzo normale di un solo piano agente sul pilastro:

N = (q_u x A_inf) + P_travi =8,54 KN/m x 14 m² + 7,605 KN = 127,263 KN

Quindi, avremo: 

N_max = N x Num_piani = 127,263 KN x 6 = 763,578 KN

 

 

Procediamo ora con il predimensionamento della sezione del pilastro, avendo f _mk, k_mod, Ɣ_m :

f_d = (0,80 x 27 MPa) / 1,45 = 14,90 MPa

 

 

Considerando alcuni dati, quali: 
E = 8000 MPa
I = 3 m
β = 1 

Si ricavano: 

λ =  π x √(E/f_cd) = π x √ (8000 MPa / 14,90 MPa) = 72,80  

ρ_min = (1 x 3 m) / 72,80 x 100 = 4,12 cm

Sapendo che per i pilastri in legno ρ_min = √ (1/12) x b , con la formula inversa avremo le dimensioni della sezione:

b_min = 4,12 cm x 3,46 = 14,27 cm

L'altra dimensione della sezione si ottiene dividendo l'area per la base trovata:

h_min = 703,73 cm²  / 14,27 cm = 49,30 cm

Tali risultati vanno ingegnerizzati, diventando:
b_design = 30 cm
h_design = 55 cm

Ultimo dato necessario per arrivare alla tensione massima è il modulo di resistenza a flessione W_max, la quale per sezioni rettangolari è: 

W_max = (b x h²) / 6 = (30 cm x 3025 cm²) / 6 = 15125,00 cm³ 

 

 

Per i pilastri B, C, D verranno seguiti gli stessi passaggi:

 

 

 

 

Inserimento della struttura in SAP

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

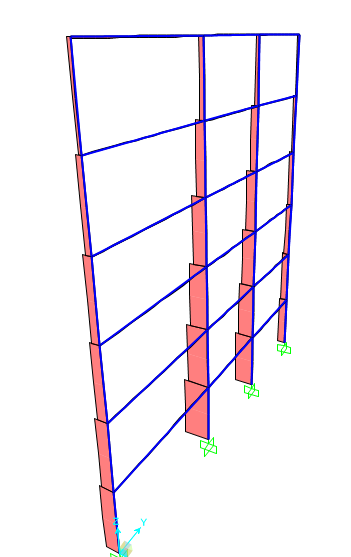
Verifica

Una volta individuato su SAP il momento flettente massimo e lo sforzo normale del pilastro maggiormente sollecitato, lo riportiamo sul file di calcolo, utilizzando la formula di verifica a pressoflessione. Quindi avremo:

W_max = modulo di resistenza a flessione = b_design x h_design² / 6 = (30 cm x 3025 cm² ) / 6 = 15125 cm³

Da qui troviamo la Tensione massima (sigma) = (N/A) + (M/W_max) = (663 KN / 1650 cm²) x (10) + (39,62 KNm / 15125 cm³) = 6,637 MPa

Tensione massima < f_d  ----> verificata.

 

 

 

 

 

CONSEGNA IN GRUPPO: Pasqualino, Pellegrini, Rossi