Esercitazione

 

 Lo scopo di questa esercitazione è quello di calcolare come viene ripartita una forza orizzontale, che sia essa considerata come la forza del vento o quella di un sisma, che agisce su una stuttura in cemento armato, costituita da telai Shear-Type, attraverso il metodo delle rigidezze.

La struttura si compone di sette telai, quattro paralleli all'asse x, e tre paralleli all'asse y:

- telaio 1v     pilastri 1-5

- telaio 2v     pilastri 2-6

- telaio 3v     pilastri 3-7-9

- telaio 4v     pilastri 4-8-10

- telaio 1o     pilastri 1-2-3-4

- telaio 2o     pilastri 5-6-7-8

- telaio 3o     pilastri 9-10

Poichè questi telai sono modellati come telai Shear-Type, è possibile calcolare la loro rigidezza in questo modo:  

                                                                       

                  

I controventi, che per il solaio rappresentano vincoli cedevoli elasticamente, possono essere schematizzati nel piano dell'impalcato come molle, aventi un’adeguata rigidezza.

Facendo riferimento ai risultati ottenuti nella quarta esercitazione EXE4 - Dimensionamento di un pilastro, i momenti d'inerzia dei pilastri saranno i seguenti:

                                    

 

Nello STEP 1 del file excel viene calcolata la rigidezza traslante associata a tutti i controventi

 

Nello STEP 2 vengono riportate tutte le rigidezze traslanti calcolate nello STEP 1, e le distanze dei controventi da un'origine arbitratria considerata come origine del sistema di riferimento O.

 

Lo STEP 3 prevede il calcolo del centro di massa che, nel caso di un impalcato con densità di massa uniforme, coincide con il centro d'area. Esso corrisponde al punto in cui verrà applicata la forza sismica.

Per rendere possibile questa operazione è necessario suddividere l'impalcato in due figure geometriche elementari, calcolarne il valore delle aree e la distanza di ognuno dei due centri d'area dall'origine O.

 

A questo punto, attraverso lo STEP 4, è possibile calcolare:

- le rigidezze totali, sia verticali che orizzontali;

- il centro delle rigidezze, con rispettive coordinate;

- la rigidezza torsionale, necessaria per il successivo calcolo della rotazione 

In questa esercitazione è previsto il dimensiomaneto e la verifica di deformabilità della mensola più sollecitata di un solaio in tre diverse tecnologie, legno, acciaio e cemento armato.
Come nelle esercitazioni precedenti sarà utilizzato un foglio excel, diviso prima nella parte di Stato Limite Ultimo (SLU) e poi in Stato Limite di Esercizio (SLE) che si usa per i valori di spostamento e deformabilità della mensola.

CALCESTRUZZO ARMATO

 

Nella mia struttura di ipotesi, la mensola maggiormento sollecitata è quella al centro con luce 6m e un interasse 6m.
Il solaio utilizzato è lo stesso con l'esercitazione di prima, quindi i valori dei carichi (strutturale, permanente, accidentale) sono gli stessi.
Per trovare il valore di carico limite ultimo dobbiamo moltiplicare ogni carico con il suo coefficiente di sicurezza.
Ottenuto il valore del carico ultimo, è ora possibile trovare il momento massimo, utilizzando la formula ql2/2, per una mensola di lunghezza l sottoposta ad un carico q.

Per progettare la trave scegliamo un calcestruzzo con resistenza fck= 60 MPa insieme con un acciaio di armatura caratterizzato da una resistenza a flessione caratteristica fyk= 450 MPa.
Fatto questo possiamo calcolare le tensioni di progetto dell'acciaio fyd e del cls fcd. Dobbiamo poi impostare la base della trave da calcolare e la dimensione del copriferro per ricavare l'altezza utile e l'altezza minima.
Scegliamo una base di 30 cm e un copriferro di 5 cm, arrivando ad una altezza minima di 35 cm.
Dato che questa sia l'altezza minima, scegliamo un'altezza di 40 cm, ottenendo una trave di sezione 30 x 40 cm.

L'utilizzo di questi dati permette di ricavare l'area e il peso della trave, valori che servono per il calcolo del carico nello SLE, dove il cemento armato ha un peso non trascurabile.
Inserendo i dati e il modulo elastico E otteniamo il valore del carico allo SLE qe, il momento d'inerzia Ix e lo spostamento massimo Vmax = 0.27 cm.
Questo valore conferma il progetto, sapendo che il rapporto tra il momento d'inerzia e lo spostamento è maggiorte di 250
 Ix/ Vmax >250

 

ACCIAIO

Per progettare la nostra trave in acciaio viene scelto un'acciaio S235 con resistenza a flessione caratteristica fyk= 235 MPa
Dato questo è possibile calcolare la tensione ammissibile di progetto fd e il modulo di resistenza Wx minimo 452 cm3.
Scegliamo una IPE 300 con modulo di resistenza Wx= a 557.1 cm3, momento d'inerzia Ix = 8356 cm4 e peso = 42.2 kg/m.
Inserendo i dati e il modulo elastico E = 210000 MPa, otteniamo i valori del carico allo SLE che tiene conto anche del peso proprio della trave e dello spostamento massimo Vmax= 0.171 cm.

        
Questo valore conferma il progetto, sapendo che il rapporto tra il momento d'inerzia e lo spostamento è maggiorte di 250
 Ix/ Vmax >250

 

LEGNO

Per il progetto della nostra trave scegliamo un legno lamellare GL24H, con resistenza a flessione caratteristica fmk= 24 MPa. Scegliamo anche un coefficiente kmod= 0.8 e come coefficiente parziale di sicurezza del materiale γm= 1.45 
Fatto questo è possibile calcolare la tensione ammissibile di progetto fd.

Dobbiamo poi impostare la base della nostra trave per ottenere l'altezza minima.
Scegliamo una base di 25 cm e otteniamo un'altezza minima di 38.73 cm. Dato che questo sia il valore minimo dell'altezza della trave otteniamo una trave di sezione 25 x 40 cm.
Dopo aver fatto la parte relativa allo SLE, inseriamo il valore del modulo elastico del legno E= 8000 MPa, che non tiene però in considerazione il peso proprio della trave (il legno è un materiale leggero), del momento d'inerzia Ix e dello spostamento massimo Vmax= 0.41 cm.
Questo valore conferma il progetto, sapendo che il rapporto tra il momento d'inerzia e lo spostamento è maggiorte di 250
 Ix/ Vmax >250

 

 

Scopo della terza esercitazione è progettare e verificare una mensola soggetta a flessione utilizzando sezioni in legno, acciaio e cls.a e verificare allo SLE che l'abbassamento massimo sia inferiore uguale al limite indicato dalla normativa.

La mensola evidenziata in figura è la più sollecitata dell'impalcato ed ha un'area di influenza di 1,80m x 3,80m = 6,84m²

Utilizzo la stessa tecnologia per i solai utilizzata nell'esercitazione precedente.

http://design.rootiers.it/strutture/node/2163

1. LEGNO

Carichi permanenti strutturali: q_s= 1,36KN/m²

Carichi permanenti non strutturali: q_p=2,6KN/m²

Carichi accidentali:Per i balconi il carico accidentale q_a = 4KN/m²

 

Inserendo tutti i dati ricavati nel foglio di calcolo excel ricavo il carico q_u = 44,34KN/m agente sulla trave.

Compilando la cella relativa alla luce ottengo invece il valore del M_max = 71,82KN*m           

Scelgo la tipologia di legno GL24h, inserisco il valore caratteristico di resistenza f_m,K=24N/mm², il coefficiente diminutivo K_mod=0,8 e il coefficiente parziale di sicurezza γ_m=1,45 in modo che il foglio di calcolo mi restituisca la tensione di progetto f_d=13,24N/mm².

Come passo successivo scelgo la base della trave b=25cm e ricavo l'altezza minima h_min=36,08cm. Ingegnerizzando la sezione ricavata ne scelgo una 25x40cm.

Inserendo ora il modulo elastico E=8GPa il foglio di calcola l'abbassamento massimo.

Infine per verificare calcolo il rapporto luce-abbassamento che deve essere maggiore di 250. VERIFICATA

1. Acciaio

Carico strutturale totale: q_s = 2,14KN/m²

Carico permanente non strutturale totale a cui aggiungo l'incidenza di impianti e tramezzi: q_p = 2,64KN/m²

Carichi accidentali: Per i balconi il carico accidentale q_a = 4KN/m²

Inserendo tutti i dati ricavati nel foglio di calcolo excel ricavo il carico q_u = 48,42KN/m agente sulla trave.

Compilando la cella relativa alla luce ottengo invece il valore del M_max = 78,43KN*m           

Scelgo la tipologia di acciaio S275, inserisco il suo valore di tensione di snervamento f_y,K=275MPa, quindi ricavo il modulo di resistenza elastico minimo W_x,min = 299,50cm³

e sul profilario scelgo una IPE con W_x>W_x,min : IPE240 con W_x= 324,3cm³

Scelta la trave inserisco nella tabella excel il momento d'inerzia I_x= 3892cm⁴ ed il peso proprio p=0,307KN/m, perché in questo caso non posso trascurare l'incidenza del peso della trave.

Dopo aver inserito anche il modulo di elasticità dell'acciaio E=210GPa.

Infine per verificare calcolo il rapporto luce-abbassamento che deve essere maggiore di 250.

VERIFICATA

 

 

1. Calcestruzzo armato

Il carico strutturale totale: q_s = 3,5KN/m²

Il carico permanente non strutturale totale a cui aggiungo l'incidenza di impianti e tramezzi: q_p = 2,94KN/m²

Carichi accidentali: Per i balconi il carico accidentale q_a = 4KN/m²

 

Inserendo tutti i dati ricavati nel foglio di calcolo excel ricavo il carico q_u = 56,85KN/m agente sulla trave.

Compilando la cella relativa alla luce ottengo invece il valore del M_max = 92,09KN*m           

Scelgo la tipologia di acciaio dei tondini B450C, inserisco il suo valore di tensione di snervamento f_y,K=450MPa, quindi ricavo la tensione di progetto f_yd=391,30MPa;

scelgo la tipologia di cemento C35/45 con resistenza caratteristica f_cK=35MPa, quindi ricavo la resistenza di progetto f_cd=19,83MPa.

Il passaggio successivo è la scelta di una dimensione per la base della sezione b=30cm che, insieme a resistenza di progetto f_cd e parametri β e r serve per trovare l'altezza utile h_u=28,94cm che addizionata al coprifilo δ=4cm determina l'altezza minima H_min=32,94cm.

Una volta ricavata l'altezza minima andiamo ad ingegnerizzare la sezione e scegliamo un'altezza di design H_design=40cm.

Il foglio calcola in automatico il peso della trave e dopo aver inserito anche il modulo di elasticità E=21GPa.

Infine per verificare calcolo il rapporto luce-abbassamento che deve essere maggiore di 250.

VERIFICATA

Il peso della trave viene aggiunto al carico totale che diventa q_u=60,75KN/m in modo da ricavare di nuovo H_min=33,91cm e se quest'ultima dimensione è inferiore a H_design la sezione è verificata.

H_min=33,91cm < H_design=40cm   VERIFICATA

 

 

Scopo dell'esercitazione è progettare e verificare una trave appoggiata soggetta a flessione utilizzando sezioni in legno, acciaio e cls.a.

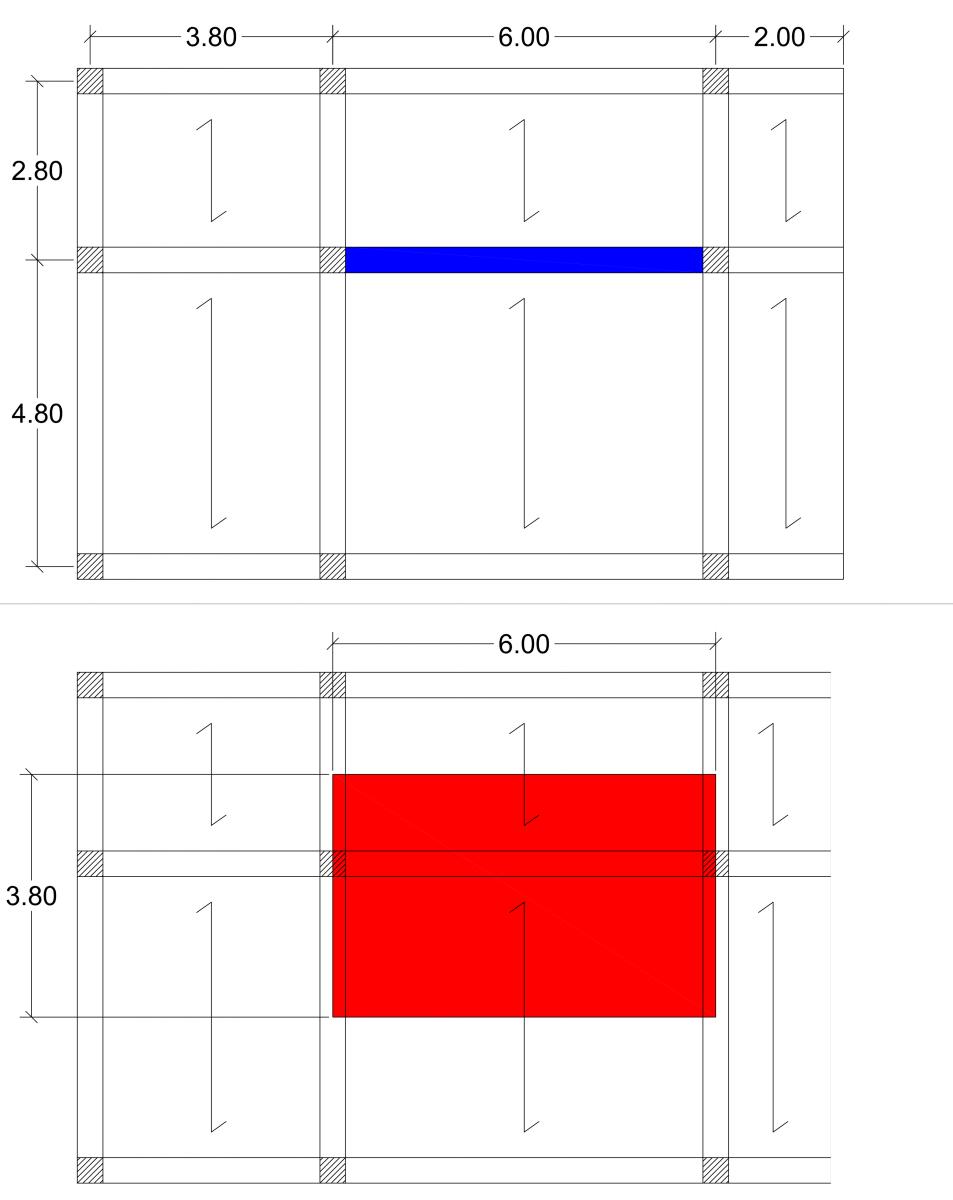
La trave evidenziata in figura è la più sollecitata dell'impalcato ed ha un'area di influenza di 6,00m x 3,80m = 22,80m²

1. Legno

Come prima operazione calcolo i carichi permanenti strutturali(trascurando il peso proprio della trave), permanenti non strutturali ed accidentali

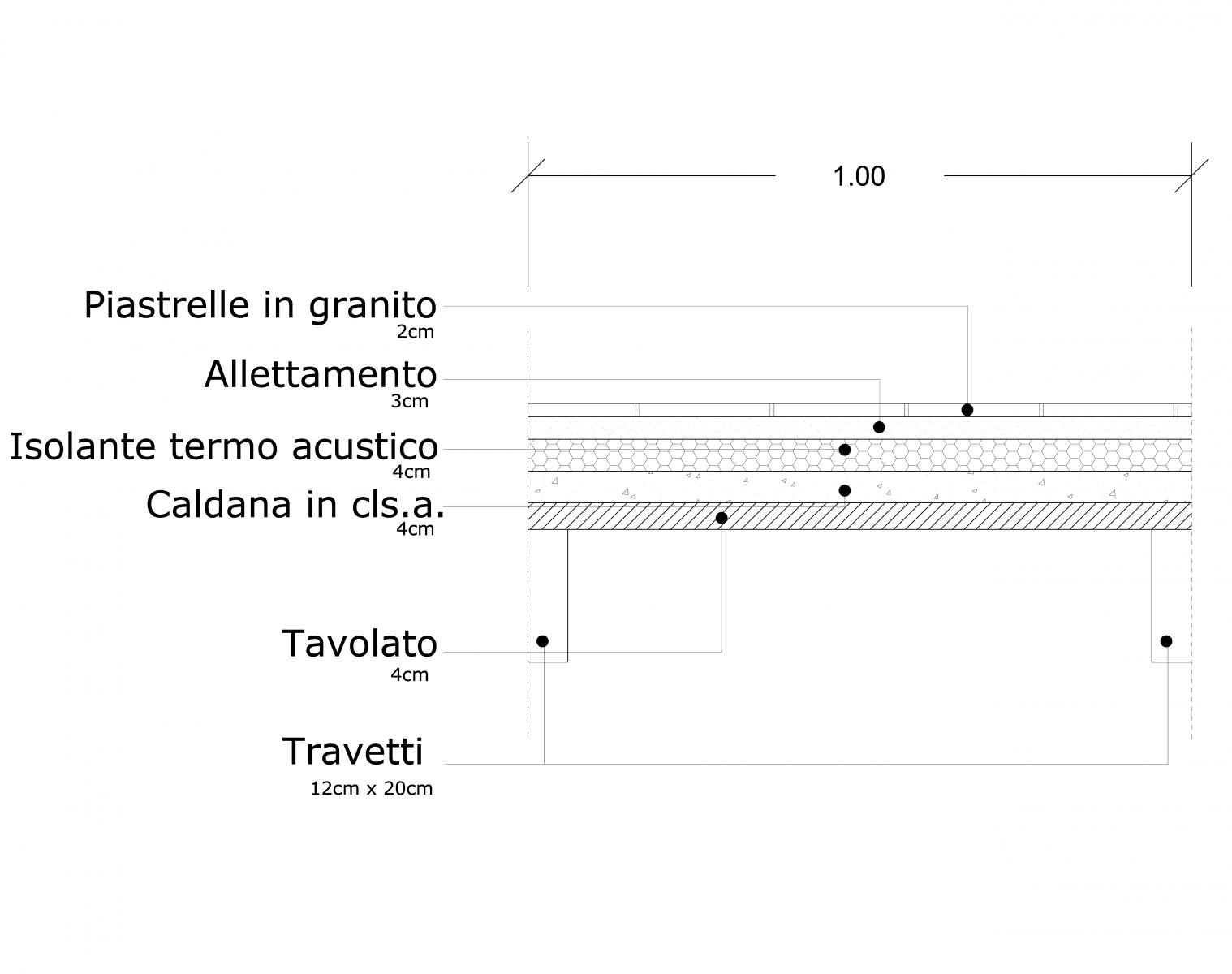
Carichi permanenti strutturali:

-Travetto in legno: (12x22)cm, peso specifico 6KN/m³, interasse 1m

q_s,tr = (0,12m x 0,22m x 1m)/m² x 6KN/m³ = 0,16KN/m²

-Tavolato in legno: spessore 4 cm, peso specifico 5KN/m³

q_s,ta = 0,04m x 5KN/m³ = 0,20KN/m²

-Caldana in cls.a.: spessore 4cm, peso specifico 25KN/m³

q_s,ca = 0,04m x 25 KN/m³ = 1,00KN/m²

Il carico strutturale totale:

q_s = q_s,tr + q_s,ta + q_s,ca  = (0,16+0,20+1,00)KN/m²  = 1,36KN/m²

Carichi permanenti non strutturali:

-Isolante termo-acustico: spessore 4cm, peso specifico 0,50KN/m³

q_p,is = 0,04m x 0,50KN/m³ = 0,02KN/m²

-Massetto di allettamento: spessore 3cm, peso specifico

q_p,ma = 0,03m x 18KN/m³ = 0,54KN/m²

-Pavimento in granito: spessore 2cm, peso specifico

q_p,pa = 0,02m x 27KN/m³ = 0,54KN/m²

Il carico permanente non strutturale totale a cui aggiungo l'incidenza di impianti e tramezzi:

q_p = q_p,is + q_p,ma + q_p,pa + q_p,im  + q_p,tr  = (0,02+0,54+0,54+0,5+1)KN/m²  = 2,6KN/m²

Carichi accidentali:

-Ipotizzo che la destinazione d'uso sia quella della categoria D1 negozio, quindi il carico accidentale q_a = 4KN/m²

• Inserendo tutti i dati ricavati nel foglio di calcolo excel ricavo il carico q_u = 44,34KN/m agente sulla trave.

Compilando la cella relativa alla luce ottengo invece il valore del M_max = 199,52KN*m        

Scelgo la tipologia di legno GL24h, inserisco il valore caratteristico di resistenza f_m,K=24N/mm², il coefficiente diminutivo K_mod=0,8 e il coefficiente parziale di sicurezza γ_m=1,45 in modo che il foglio di calcolo mi restituisca la tensione di progetto f_d=13,24N/mm²

Come passo successivo scelgo la base della trave b=30cm e ricavo l'altezza minima h_min=49,32cm. Ingegnerizzando la sezione ricavata dovrei sceglierne una 30x55cm, ma avendo trascurato il peso proprio della trave ne scelgo una 30x60cm.

Anche se non strettamente necessario calcolo il peso proprio della trave e lo aggiungo al carico permanente strutturale q_s: 

q_s,trave = (0,30m x 0,55m x 1m)/m² x 6KN/m³ = 0.99KN/m²

quindi

q_s = q_s,tr + q_s,ta + q_s,ca + q_s,trave = (0,16+0,20+1,00+0.99)KN/m²= 2,35KN/m²

inserendo il nuovo q_s verifico che il nuovo h_min=57,84cm<h=60cm  VERIFICATA

 

1. Acciaio

Come prima operazione calcolo i carichi permanenti strutturali(trascurando il peso proprio della trave), permanenti non strutturali ed accidentali

Carichi permanenti strutturali:

-Trave secondaria IPE180: area 23,95cm², peso specifico 78,5KN/m³, interasse 0,5m

q_s,tr = (0,0024m² x 1m)/m² x 78,5KN/m³ = 0,1884KN/m²

-Lamiera grecata: altezza 9 cm, spessore 1,2mm, peso 0,15KN/m²

q_s,la = 0,15 KN/m²

-Caldana in cls.a.: volume: (0,05m² x 1m)+(0,005m² x 1m) x 4 = 0,072m³/m², peso specifico 25KN/m³

q_s,ca = 0,072m³/m² x 25 KN/m³ = 1,8KN/m²

Il carico strutturale totale:

q_s = q_s,tr + q_s,la + q_s,ca  = (0,1884+0,15+1,8)KN/m² = 2,1384KN/m² ≈ 2,14KN/m²

Carichi permanenti non strutturali:

-Isolante termo-acustico: spessore 4cm, peso specifico 0,50KN/m³

q_p,is = 0,04m x 0,50KN/m³ = 0,02KN/m²

-Massetto di allettamento: spessore 4cm, peso specifico 18KN/m³

q_p,ma = 0,04m x 18KN/m³ = 0,72KN/m²

-Pavimento in gres: spessore 2cm, peso specifico 0,4KN/m²

q_p,pa = 0,4KN/m²

Il carico permanente non strutturale totale a cui aggiungo l'incidenza di impianti e tramezzi:

q_p = q_p,is + q_p,ma + q_p,pa  + q_p,im  + q_p,tr  = (0,02+0,72+0,4+0,5+1)KN/m² = 2,64KN/m²

Carichi accidentali:

-Ipotizzo che la destinazione d'uso sia quella della categoria D1 negozio, quindi il carico accidentale q_a = 4KN/m²

 

Inserendo tutti i dati ricavati nel foglio di calcolo excel ricavo il carico q_u = 48,42KN/m agente sulla trave.

Compilando la cella relativa alla luce ottengo invece il valore del M_max = 217,89KN*m         

Scelgo la tipologia di acciaio S275, inserisco il suo valore di tensione di snervamento f_y,K=275MPa, quindi ricavo il modulo di resistenza elastico minimo W_x,min = 831,94cm³

e sul profilario scelgo una IPE con W_x>W_x,min : IPE360 con W_x= 903,6cm³

Calcolo il peso proprio della trave e lo aggiungo al carico permanente strutturale q_s:

q_s,trave = (0,0073m² x 1m)/m² x 78,5KN/m³ = 0, 57KN/m²

quindi

q_s = q_s,tr + q_s,la + q_s,ca + q_s,trave = (0,1884+0,15+1,8+0,57)KN/m²=2.7KN/m²

 inserendo il nuovo q_s verifico che il nuovo W_x,min=879,47cm³<W_x=903,6cm³ VERIFICATA

 

1. Calcestruzzo armato

Come prima operazione calcolo i carichi permanenti strutturali(trascurando il peso proprio della trave), permanenti non strutturali ed accidentali

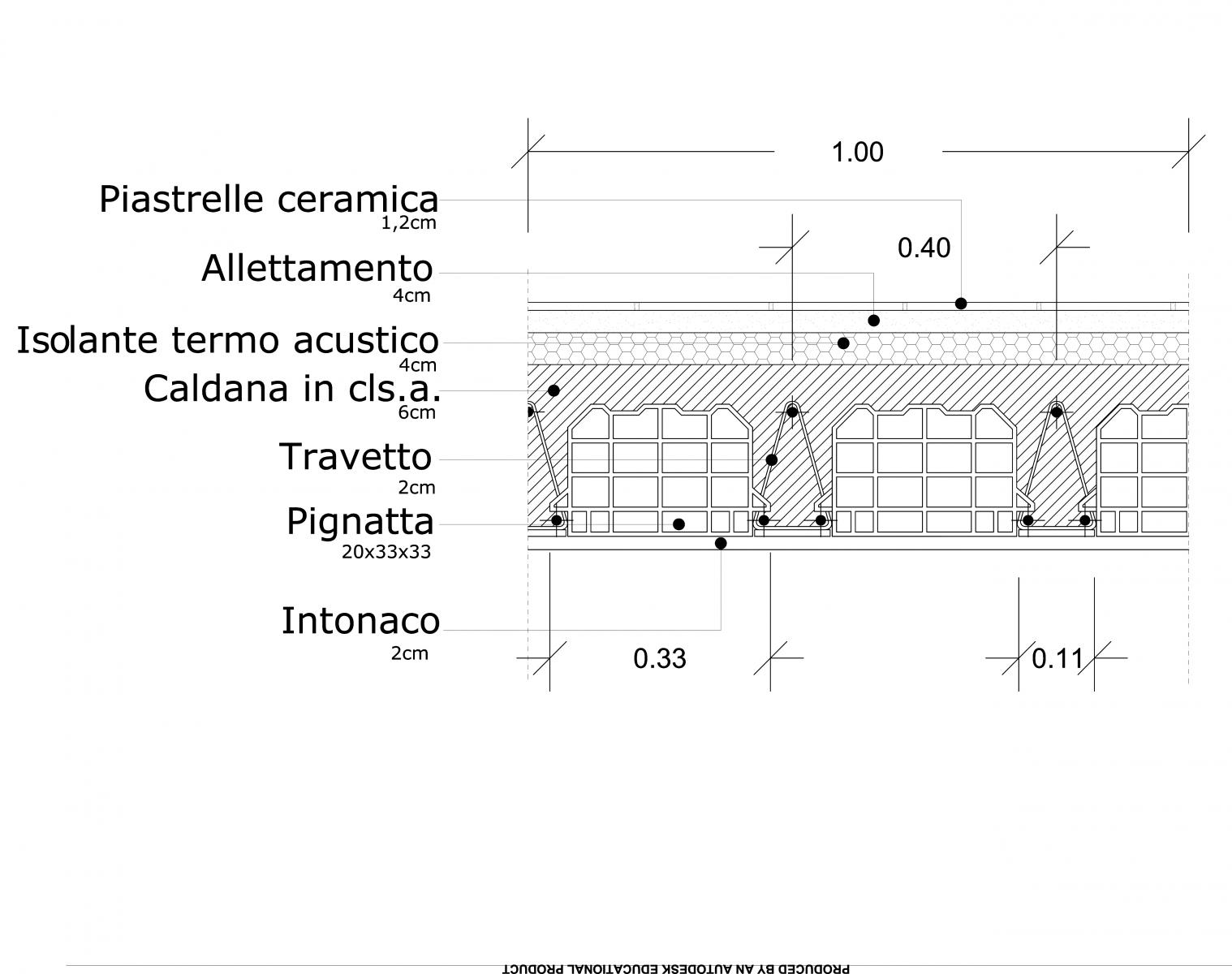
Carichi permanenti strutturali:

-Travetto prefabbricato: dim 20cm x 11 cm, peso specifico 24N/m³, interasse 0,4m:

2,5 travetti/m²

q_s,tr =n_tr x (0.2x0.11x1)m³/m² x 24KN/m³ =2,5 x  0,53KN/m²=1,325KN/m²

-Pignatta in laterizio: dim 20cm x 33cm x 33cm, peso al pz 9,2Kg ≈ 0,092KN/m², interasse 0,4m: 7,5 pignatte/m²

q_s,pi = n_pi x 0,092KN/m²=7,5 x 0,092KN/m² = 0,69KN/m²

-Caldana in cls.a.: spessore 6cm, peso specifico 25KN/m³

q_s,ca = 0,06m x 25 KN/m³ = 1,50KN/m²

Il carico strutturale totale:

q_s = q_s,tr + q_s,pi + q_s,ca  = (1,325+0,69+1,5)KN/m² = 3,515KN/m² ≈ 3,5KN/m²

Carichi permanenti non strutturali:

-Isolante termo-acustico: spessore 4cm, peso specifico 0,50KN/m³

q_p,is = 0,04m x 0,50KN/m³ = 0,02KN/m²

-Massetto di allettamento: spessore 4cm, peso specifico 18KN/m³

q_p,ma = 0,04m x 18KN/m³ = 0,72KN/m²

-Pavimento in ceramica: spessore 1,2cm, peso specifico 0,2KN/m²

q_p,pa = 0,2KN/m²

-Intonaco: spessore 2cm, peso specifico 16 KN/m³

q_p,in = 0,02m x 16KN/m³ = 0,32KN/m²

Il carico permanente non strutturale totale a cui aggiungo l'incidenza di impianti e tramezzi:

q_p = q_p,is +q_p,ma+q_p,pa + q_p,in+ q_p,im +q_p,tr =(0,02+0,72+0,32+0,2+0,5+1)KN/m²=2,94KN/m²

Carichi accidentali:

-Ipotizzo che la destinazione d'uso sia quella della categoria D1 negozio, quindi il carico accidentale q_a = 4KN/m²

 

Inserendo tutti i dati ricavati nel foglio di calcolo excel ricavo il carico q_u = 56,85KN/m agente sulla trave.

Compilando la cella relativa alla luce ottengo invece il valore del M_max = 255,82KN*m         

Scelgo la tipologia di acciaio dei tondini B450C, inserisco il suo valore di tensione di snervamento f_y,K=450MPa, quindi ricavo la tensione di progetto f_yd=391,30MPa;

scelgo la tipologia di cemento C35/45 con resistenza caratteristica f_cK=35MPa, quindi ricavo la resistenza di progetto f_cd=19,83MPa.

Il passaggio successivo è la scelta di una dimensione per la base della sezione b=30cm che, insieme a resistenza di progetto f_cd e parametri β e r serve per trovare l'altezza utile h_u=48,23cm che addizionata al coprifilo δ=4cm determina l'altezza minima H_min=52,23cm.

Una volta ricavata l'altezza minima andiamo ad ingegnerizzare la sezione e scegliamo un'altezza di design H_design=60cm. 

Il foglio excel in automatico calcola il peso della trave, prima trascurato, e lo aggiunge carico totale che diventa q_u=62,70KN/m in modo da ricavare di nuovo H_min=54,65cm e se quest'ultima dimensione è inferiore a H_design la struttura è verificata.

H_min=54,65cm< H_design=60cm   VERIFICATA

Per questa esercitazione modifico la struttura dell'esercitazione precedente in modo da ottenere una trave a sbalzo, mantengo gli stessi solai con gli stessi materiali in modo da ottenere una comparazione più diretta con l'esercitazione precedente.

INTERASSE: 3m

LUCE: 3m

AREA DI INFLUENZA: 9mq

In questa esercitazione dovrò dimensionare una trave a sbalzo nei tre materiali con una verifica a deformabilità (similmente alla seconda esercitazione) dopodichè dovrò controllare l'abbassamento minimo dell'elemento effettuando le verifiche allo SLE.

La prima parte dell'esercizio riguardante il dimensionamento sarà pressochè uguale alla seconda esercitazione tranne che per due valori, il momento massimo non sarà più quello di una trave appoggiata appoggiata ma quello di una mensola  Mmax=q_ul²/2

Inoltre il carico accidentale qua è pari a 4 KN/mq come da normativa per carichi accidentali su balconi.

legno- Sezione 25x45

acciaio- IPE 330

calcestruzzo armato- Sezione 30x40

Una volta dimensionate le sezioni allo SLU passiamo alla verifica a deformabilità allo SLE (poichè è una verifica finalizzata a controllare che non vi siano spostamenti e deformazioni che ne compromettano l'uso) con le conseguenti diverse combinazioni di carico incidenti.

Inoltre in questa verifica per quanto riguarda l'acciaio verrà presa in considerazione l'influenza del suo peso proprio (per una IPE 330 è di 0,49 KN/m) all'interno del calcolo del carico totale.

Anche per la verifica del calcestruzzo viene presa in considerazione l'influenza del peso, nel legno invece continua a essere ignorato.

Per il calcolo dello spostamento oltre al momento massimo ho bisogno di altre due informazioni: il modulo di elasticità dipendente dal materiale e il momento di inerzia dipendente dalla sezione.

Questi mi servono per potermi ricavare in primis la curvatura χ = (qx²/2) (1/EI), da cui mi ricaverò la rotazione   ϕ = (qx³/6) (1/EI) + C₁ da cui mi posso infine ricavare (sostituendo le costanti di integrazione) l' abbassamento massimo Vmax=ql⁴/8EI

Una volta trovato il valore dell'abbassamento massimo posso verificare che il rapporto tra questo e la luce della trave sia maggiore di 250, come imposto dalla normativa.

legno= verificato

acciaio=verificato

calcestruzzo armato=verificato

 

Dato questo telaio dimensioniamo la mensola, che ha un aggetto di 2,50 m

 

 

 

 

 

 

 

 

 

 

 

ANALISI DEI CARICHI PER SOLAIO IN ACCIAIO 

 

 

 

 

 

Elementi del Solaio

Lamiera Grecata – spessore: 0.9 mm; altezza: 7 cm; Peso: 0,11 KN/m²

Getto di cls – altezza: 7 cm nella lamiera + 4 cm esterni; Peso Specifico: 25 KN/m³

Isolante – altezza 3 cm; Peso Specifico: 1,8 KN/m³

Massetto – altezza: 5 cm; Peso Specifico: 19 KN/m³

Pavimento – altezza: 3 cm; Peso Specifico: 20 KN/m³

 

Calcolo Carichi Strutturali

Lamiera Grecata: 0,11 KN/m²

Getto di cls: (25 KN/m³ x 0,04 m) + (25 KN/m³ x 0,07m) / 2 = 1 KN/m² + 0,875 KN/m² = 1,875 KN/m²

q_s= 0,11 KN/m² + 1,875 KN/m² = 1,985 KN/m²

 

Calcolo Carichi Permanenti

Isolante: 1,8 KN/m³ x 0,03m = 0,054 KN/m²

Massetto: 19 KN/m³ x 0,05 m = 0,95 KN/m²

Pavimento: 20 KN/m³ x 0,03 m = 0,6 KN/m²

Tramezzi: 1 KN/m²

Impianti: 0,5 KN/m²

q_p= 0,054 KN/m² + 0,95 KN/m² + 0,6 KN/m² + 1 KN/m² + 0,5 KN/m² = 3,104 KN/m²

 

Calcolo Carichi Accidentali

I carichi accidentali sono dati dalla normativa: essendo ad uso residenziale abbiamo che

q_a = 2 KN/m² 

DIMENSIONAMENTO A FLESSIONE

Una volta trovati tutti i carichi inserisco nella tabella excel (nella sezione acciaio) i valori dei carichi ricavati, l'interasse, la luce della trave e scelgo una classe di acciaio (S275), in modo che moltiplicando i carichi per i loro coefficenti di sicurezza, moltiplicandoli per l'interasse e sommandoli, ottengo il mio carico ripartito sulla trave q_u.

So che il Momento massimo di una mensola sottoposta a un carico ripartito equivale a qL²/2; sapendo tutti i valori lo calcolo e grazie a questo mi trovo il W_{x min} (=M_max/f_yd).

Grazie a questo valore trovo un profilato industralizzato adeguato, ovvero con un W_x > W_{x min}: una IPE 270.

Dal profilario vedo i valori del peso e del Momento d'inerzia e li inserisco nella tabella insieme al modulo elastico E del materiale in modo da calcolare allo SLE l'abbassamento massimo della mensola e il rapporto luce-abbassamento che deve essere maggiore di 250 per avere condizioni vivibili.

 

 

 

 

 

ANALISI DEI CARICHI PER SOLAIO IN LATEROCEMENTO

 

 

 

 

 

Elementi del Solaio

Calcestruzzo armato – altezza: 5 cm + 25x10 cm dei travetti; Peso Specifico: 25 KN/m³

Pignatte – 12x50x25 cm; Peso: 1,05 KN/m² con travetti di interasse 60 cm

Isolante – altezza 3 cm; Peso Specifico: 1,8 KN/m³

Massetto – 5 cm; Peso Specifico: 19 KN/m³

Pavimento – 3 cm; Peso Specifico: 20 KN/m³

 

Calcolo Carichi Strutturali

Cls armato: 25 KN/m³ x 0,05m + [(0,025 m³ x 2) x 25 KN/m³] / m² = 1,25 KN/m² + 1,25 KN/m² = 2,5 KN/m²

Pignatte: 1,05 KN/m²

q_s= 2,5 KN/m² + 1,05 KN/m² = 3,55 KN/m²

 

Calcolo Carichi Permanenti

Isolante: 1,8 KN/m³ x 0,03m = 0,054 KN/m²

Massetto: 19 KN/m³ x 0,05 m = 0,95 KN/m²

Pavimento: 20 KN/m³ x 0,03 m = 0,6 KN/m²

Tramezzi: 1 KN/m²

Impianti: 0,5 KN/m²

q_p= 0,054 KN/m² + 0,95 KN/m² + 0,6 KN/m² + 1 KN/m² + 0,5 KN/m² = 3,104 KN/m²

 

Calcolo Carichi Accidentali

I carichi accidentali sono dati dalla normativa: essendo ad uso residenziale abbiamo che

q_a = 2 KN/m² 

 

DIMENSIONAMENTO A FLESSIONE

Trovo q_u nuovamente grazie ai carichi, i coefficenti e l'interasse e di conseguenza il Momento massimo. Inserisco le tensioni caratteristiche f_k di cls e acciaio (C60 e S450) e trovo le tensioni caratteristiche di progetto f_cd e f_yd grazie ai coefficenti.

A questo punto scelgo una dimensione per la base della mia trave (30 cm) e per il mio copriferro (5 cm) e grazie alla tabella excel ottengo un'altezza minima di 41,28 cm. Quindi ho scelto una trave 30x45, verificata anche aggiungendo il peso proprio. Inserendo il modulo elastico E del materiale calcolo l'abbassamento massimo ed il rapporto l/v_max > 250

 

 

 

 

ANALISI DEI CARICHI PER SOLAIO IN LEGNO

 

 

 

 

 

Elementi del Solaio

Travetti – altezza: 10x20cm con 50cm di interasse; Peso Specifico: 4 KN/m³ (abete rosso)

Tavolato – altezza: 3 cm; Peso Specifico: 4 KN/m³ (abete rosso)

Isolante – altezza 3 cm; Peso Specifico: 1,8 KN/m³

Massetto – 5 cm; Peso Specifico: 19 KN/m³

Pavimento – 3 cm; Peso Specifico: 20 KN/m³

 

Calcolo Carichi Strutturali

Travetti: [(0,02 m³ x 2) x 4 KN/m³] / m² = 0,16 KN/m²

Tavolato: 4 KN/m³ x 0,03 m = 0,12 KN/m²

q_s= 0,16 KN/m² + 0,12 KN/m² = 0,28 KN/m²

 

Calcolo Carichi Permanenti

Isolante: 1,8 KN/m³ x 0,03m = 0,054 KN/m²

Massetto: 19 KN/m³ x 0,05 m = 0,95 KN/m²

Pavimento: 20 KN/m³ x 0,03 m = 0,6 KN/m²

Tramezzi: 1 KN/m²

Impianti: 0,5 KN/m²

q_p= 0,054 KN/m² + 0,95 KN/m² + 0,6 KN/m² + 1 KN/m² + 0,5 KN/m² = 3,104 KN/m²

 

Calcolo Carichi Accidentali

I carichi accidentali sono dati dalla normativa: essendo ad uso residenziale abbiamo che

q_a = 2 KN/m² 

 

DIMENSIONAMENTO A FLESSIONE

Nuovamente, trovati i diversi carichi trovo il carico distribuito q_u e calcolo il Momento massimo. A questo punto inserisco la tensione caratteristica del materiale da me scelto (Abete rosso) f_mk = 24 MPa, che moltiplicato per il fattore di umidità k_mod e diviso per il coefficente di sicurezza dà la tensione caratteristica di progetto  f_md.

Fatto questo scelgo un valore per la mia base, scegliendo tra i valori industrializzati (24 cm), trovo un'altezza minima pari a 44,24 cm, dunque scelgo un profilato 24x48 cm (sempre controllando tra i valori industrializzati).

Inserisco il modulo elastico E del materiale e calcolo l'abbassamento massimo ed il solito rapporto luce-abbassamento che deve sempre essere maggiore di 250.