Blog

Step 1:

Dato un impalcato in calcestruzzo armato come in figura con pilastri 400x600, calcolo le ripartizione delle forze orizzontali attraverso il metodo delle rigidezze.

Si identificano nell' impalcato tutti i telaio che fungono da controventi per le forze orizzontali che agiscono sulla struttura, quindi:

v1 - pilastri: 1-4-7-9

v2 - pilastri: 2-5-8-10

v3 - pilastri: 3-6

 

o1 - pilastri: 1-2-3

o2 - pilastri: 4-5-6

o3 - pilastri: 7-8

o4 – pilastri: 9-10

---

Il Modulo di Yang è pari a 21000 N/mm² per il calcestruzzo, l' altezza dell' impalcato è 3,00m, successivamente calcolo i due momenti di inerzia negli assi x e y del profilo rettangolare pari a Ix = bh³/12  e Iy = b³h/12 (72000 cm⁴ e 32000 cm⁴). Faccio delle semplificazioni e  considero l’ impalcato come una struttura a telaio Shear-Type con infinita rigidità assiale. Questo ci permette di calcolare la rigidezza traslante K_T di ogni telaio:

k= (12 EI) / h³

Calcolando la somma delle rigidezze dei singoli pilastri, riusciamo a determinare la rigidezza traslante di tutto il telaio, poiché il telaio Shear-Type ha una rigidezza pari a:

K_telaio= (12 E) / h³ x sommatoria dei Momenti di Inerzia

---

Step 2:

Si riportano in tabella tutte le rigidezze calcolate prima, con relative distanze tra esse e l’origine degli assi posto in basso a sinistra dell’impalcato:

---

Step 3:

Data la difficoltà nel trovare il centro di massa G(Xg;yg) si scompone, come in figura, la struttura in due parti.

Troviamo le coordinate del centro d’area dell’ impalcato facendo il rapporto tra la somma delle aree moltiplicate per le rispettive coordinate dei propri centro d’ area e l’ area totale dell’ impalcato.

---

Step 4:

La tabella si divide in due parti:

• Prima calcoliamo le rigidezze totali sia in direzione verticali che orizzontali sommando tutte le rigidezze dei controventamenti nello step 1.
• Poi viene calcolata “Kφ” la rigidezza torsionale che si ricava tramite la sommatoria di tutte le rigidezze ricavate nello step-1 per la loro distanza dal centro delle rigidezze, ricavato nello step-4.

---

Step 5:

A questo punto si ricavano i carichi G(kN) e Q(kN), in accordo con le norme tecniche vigenti, dalle seguenti formule:

G = (Qs + Qp) x A_tot

Q = Qa x A_tot

Si distinguono due carichi differenti per il calcolo:

 W(kN)= peso sismico: poiché il carico G rappresenta il carico strutturale e il sovraccarico permanente, mentre il carico Q racchiude tutti i carichi accidentali moltiplicati con un coefficiente di contemporaneità ψ dato da normativa.

W = G + (Q x ψ)

Questo carico W rappresenta il peso sismico e poiché ha un’accelerazione più piccola di quella di gravità, si moltiplica alla forza peso con un coefficiente riduttivo da normativa (c) secondo la sismicità del luogo:

F = W x c 

---

Step-6-7:

Si dovrà ora quantificare la ripartizione, per ogni singolo controvento, della forza sismica F lungo l’asse x e lungo quello y. L’impalcato scelto ha il centro di massa non coincidente con il centro delle rigidezze: questo comporta, nel momento che la forza sismica agisce, una traslazione e una rotazione.

Per poter conoscere il valore di questa rotazione, si calcola:

•  Momento Torcente M per l’asse x, moltiplicando la forza sismica F per il suo braccio, ovvero la differenza tra l’ordinata del centro delle rigidezze e quella del centro di massa, e per l’asse y, utilizzando come braccio la differenza tra le ascisse dei due centri.
• Traslazione orizzontale, facendo il rapporto tra F e la rigidezza totale orizzontale;
• Traslazione verticale, facendo il rapporto tra F e la rigidezza totale verticale,
• Le conseguenti Rotazioni, dividendo i rispettivi Momenti Torcenti per la rigidezza torsionale totale “Kφ” (kN/m):

L’obiettivo di questa quinta esercitazione è quello di calcolare come viene ripartita una forza orizzontale, come ad esempio quella sismica o quella del vento, su un telaio che compone una struttura, applicando il metodo delle rigidezze. 

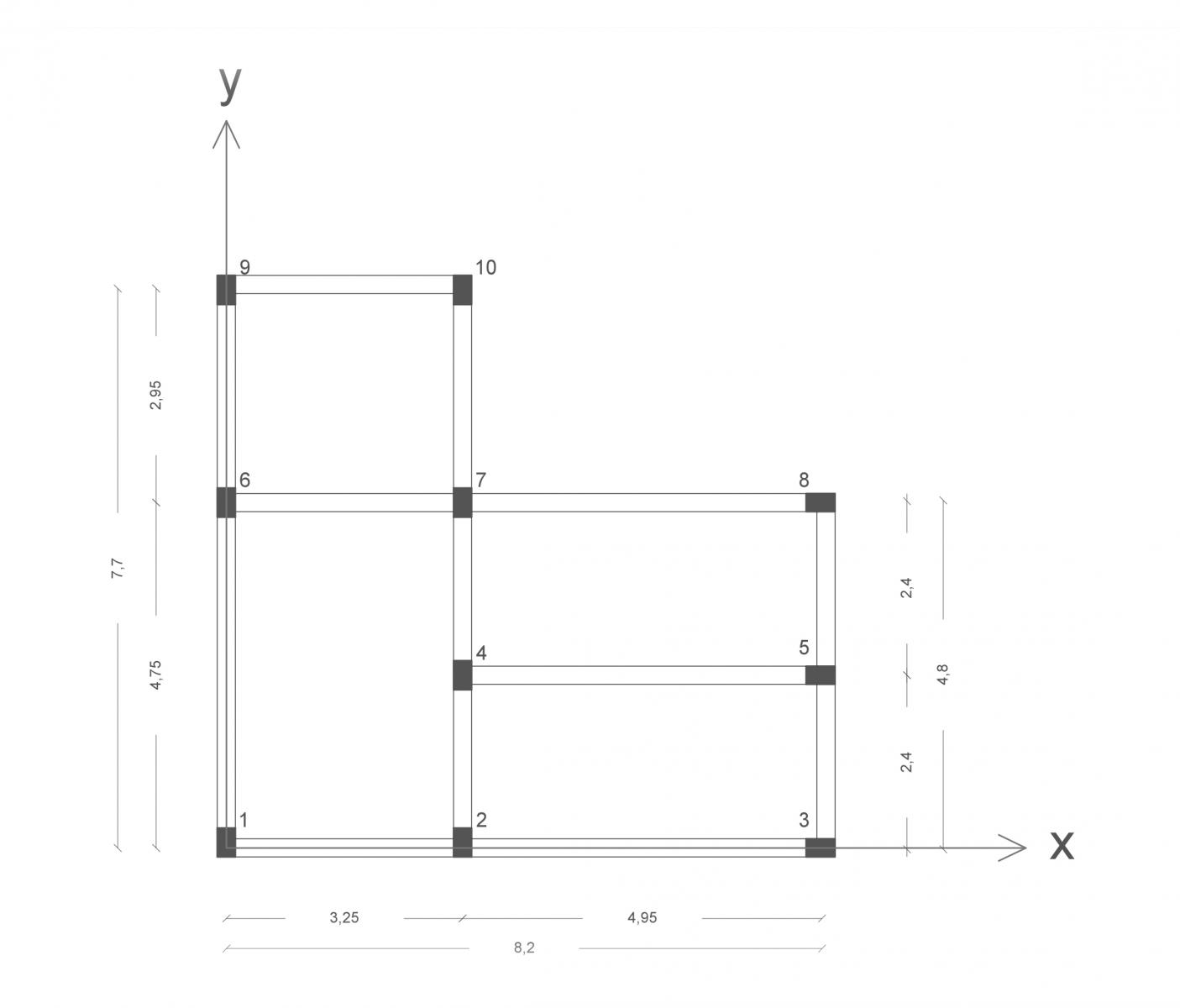
Si prende in considerazione un edificio in calcestruzzo armato ad un solo piano la cui struttura è composta da telai piani. Questi elementi strutturali, oltre a trasmettere i carichi verticali alle fondazioni, possono svolgere il ruolo di controventi poiché sono in grado di sopportare anche le azioni orizzontali.

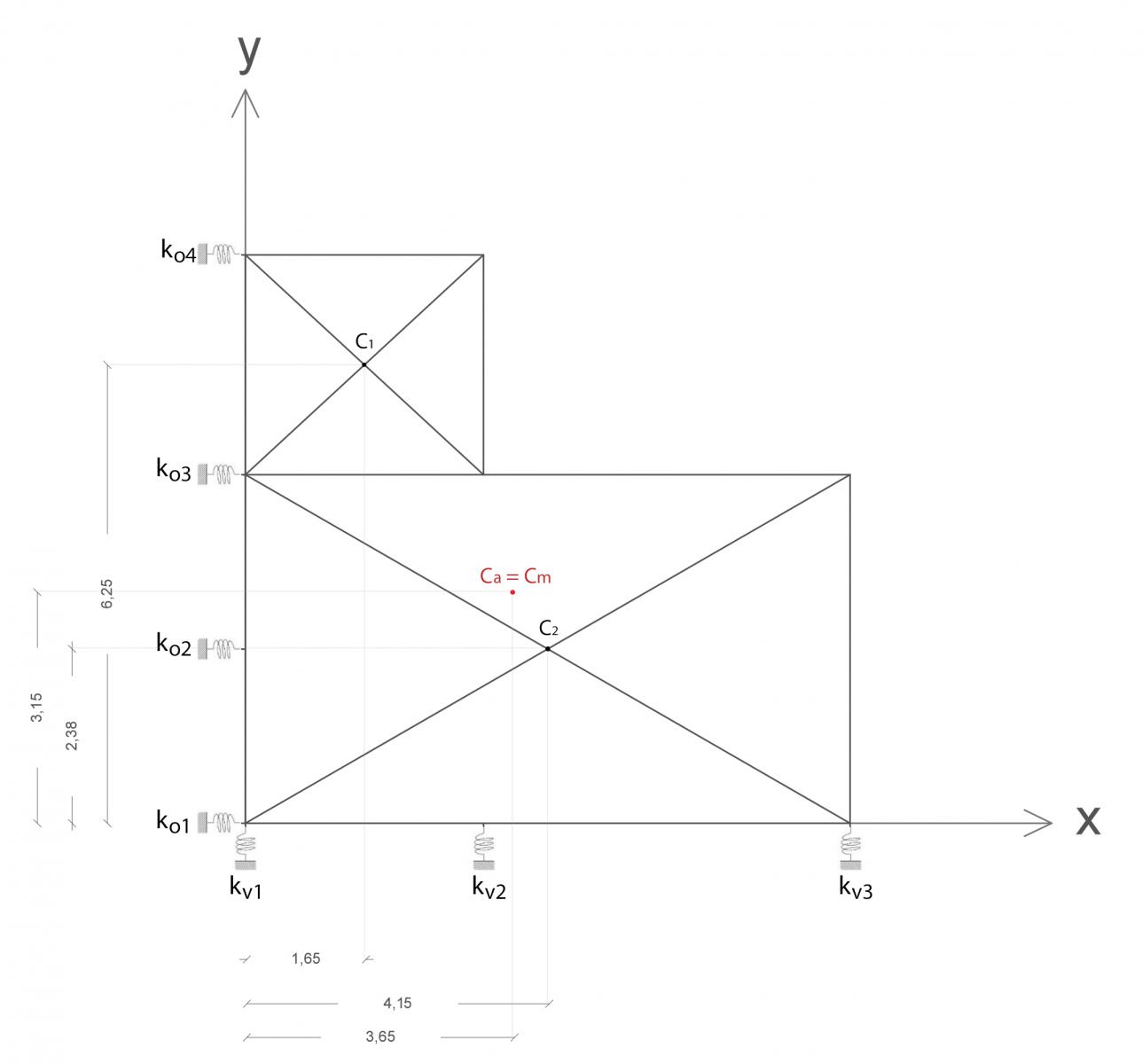
Nella pianta strutturale si possono individuare 7 telai, 3 paralleli all’asse y e 4 paralleli all’asse x:

1v --> pilastri  1-6-9                             1o --> pilastri  1-2-3-4

2v --> pilastri  2-4-7-10                        2o --> pilastri 4-5

3v --> pilastri 3-5-8                              3o --> pilastri 6-7-8

                                                            4o --> pilastri 9-10

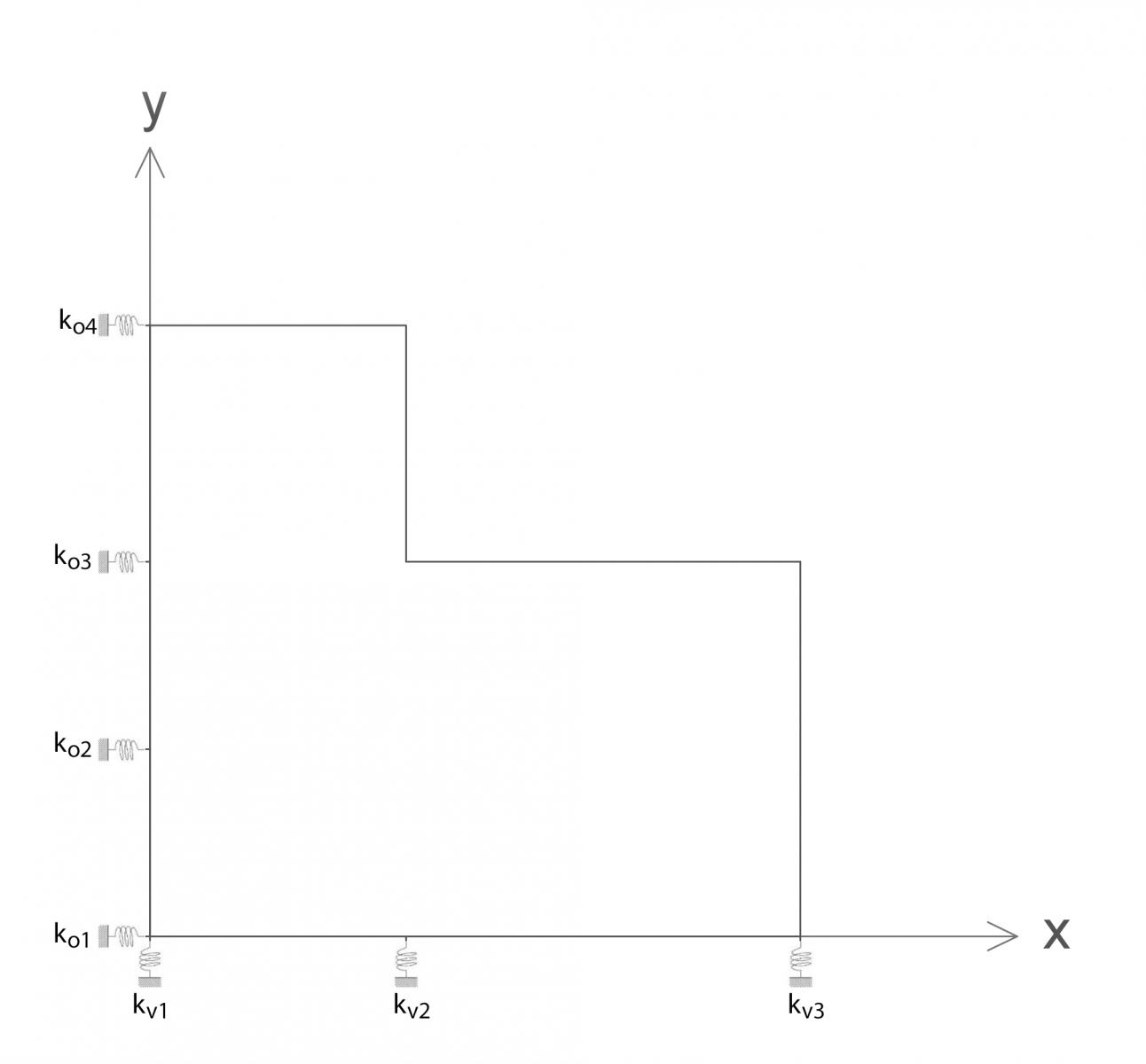
I controventi, essendo vincoli cedevoli elasticamente, possono essere schematizzati nel piano dell'impalcato come molle, aventi ognuno una propria rigidezza.

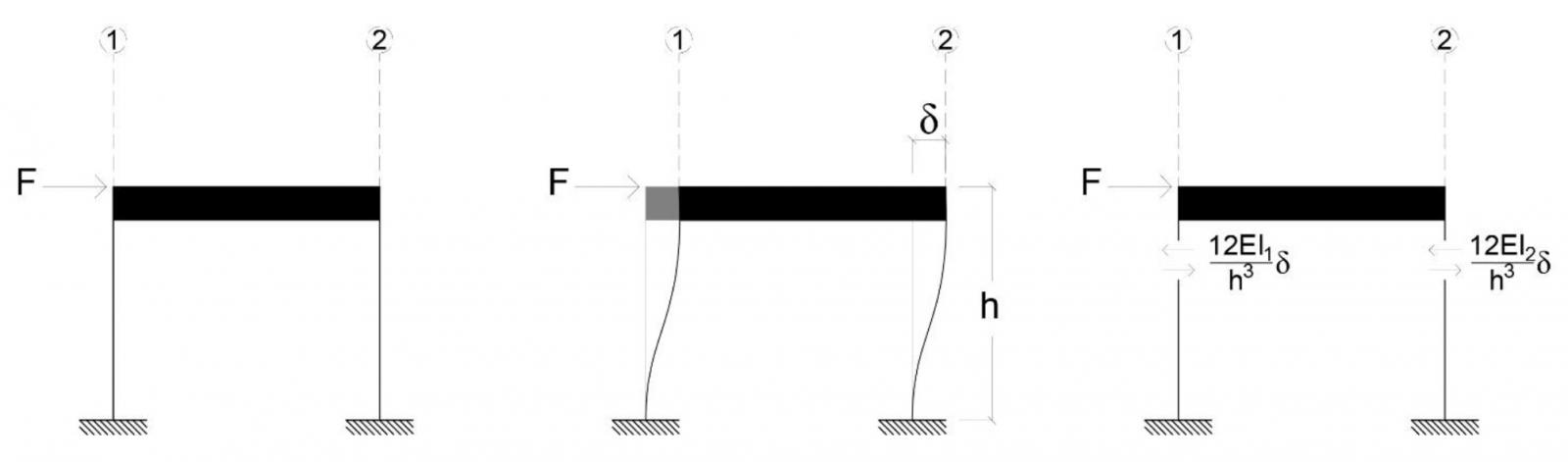
Ipotizzando che ogni telaio sia modellato come Shear-Type, la rigidezza si calcola come segue:

F = (12EI₁ / h³ + 12EI₂ / h³) d

F = k d

k = (12EI₁ / h³ + 12EI₂ / h³)

E’ possibile dunque calcolare la rigidezza traslante associata ad ogni controvento sommando le rigidezze dei singoli pilastri che lo compongono.

 

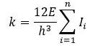
E = modulo elastico cls armato = 21000 Mpa                         

I = momento d’inerzia del pilastro che varia a seconda dell’orientamento -->       I_x = bh³ / 12                  I_y = b³h / 12

       

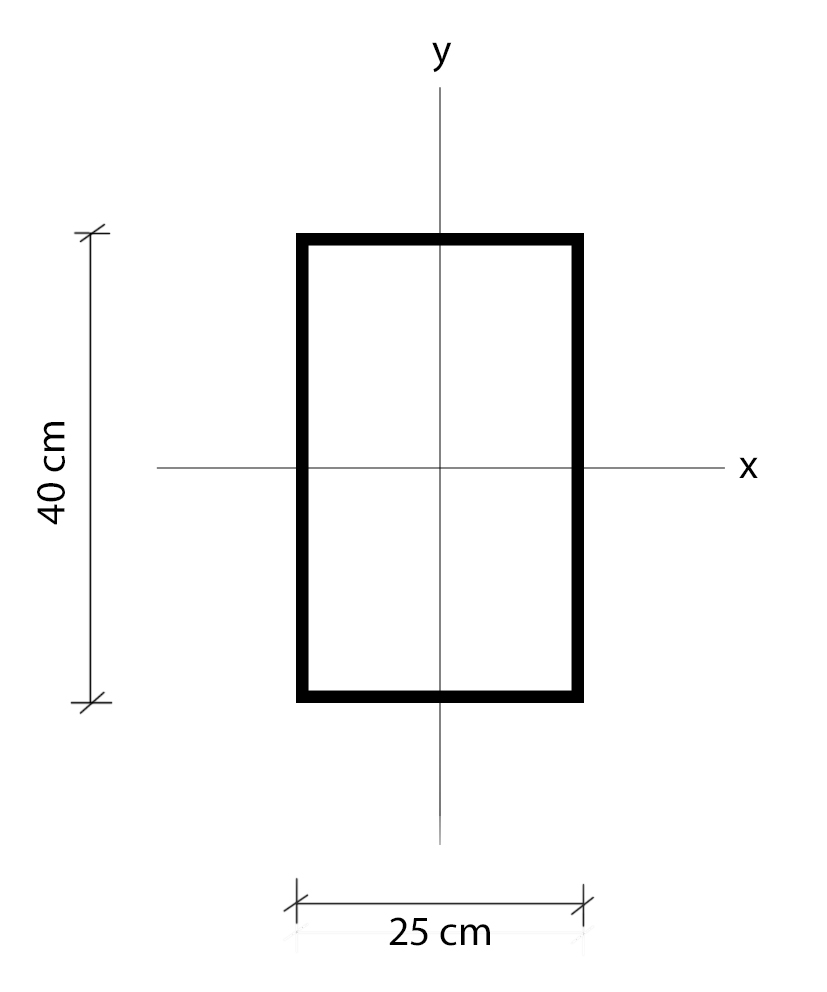
    Sezione del pilastro

    b = 25 cm

    h = 40 cm

    Ix = 133333,33 cm⁴

    Iy = 52083,33 cm⁴  

 

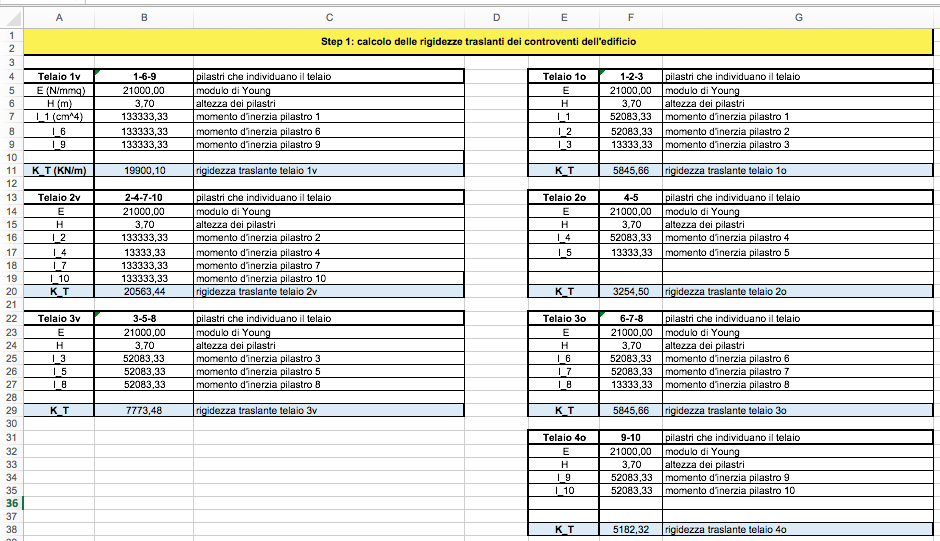
Di seguito sono riportati, in una tabella riassuntiva, i valori delle rigidezze dei controventi e le relative distanze dall’ origine.

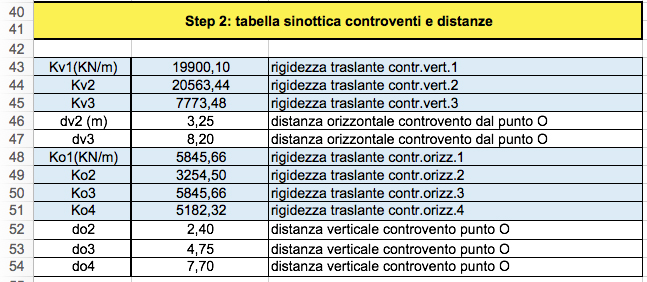
A questo punto è necessario calcolare le coordinate del centro di massa. In questo caso quest’ ultimo coincide con il centro d’area perché si ipotizza che la densità di massa sia uniforme su tutto l’impalcato.

Si suddivide l’impalcato in figure elementari e vengono indicati i centri d’area di ognuna di queste figure. A questo punto le coordinate del centro di massa valgono:

xC_m = A₁ xC₁ + A₂ xC₂ / A_tot  = 3,65

yC_y = A₁ yC₂ + A₂ yC₂ / A_tot = 3,15

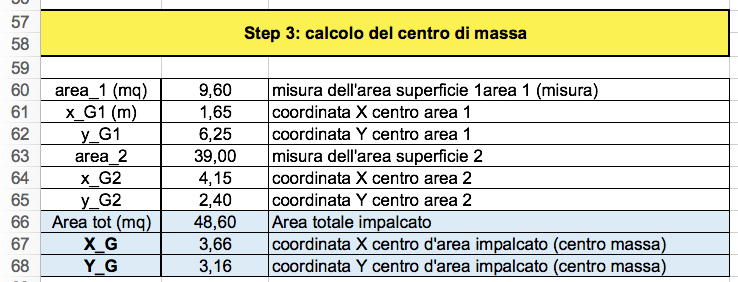
Ora è possibile calcolare:

• rigidezza totale orizzontale, somma delle rigidezze dei singoli controventi orizzontali;
• rigidezza totale verticale, somma delle rigidezze dei singoli controventi verticali;
• coordinate del centro delle rigidezze;
• rigidezza torsionale totale.

 

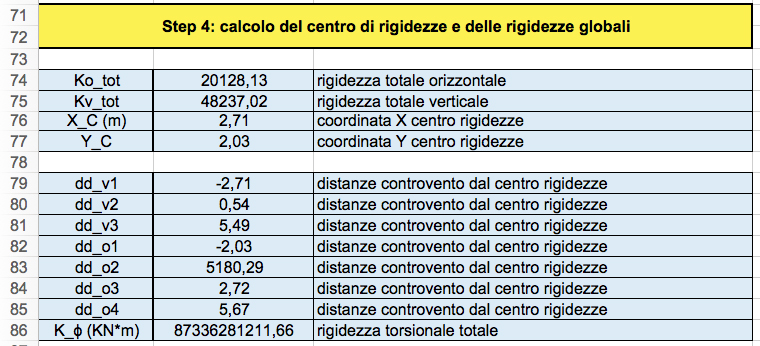
Le coordinate del centro di rigidezza valgono:

x_c = k_v1 d_v1 + k_v2 d_v2 + k_v3 d_v3 / k_v,tot = 2,71

y_c = k_o1 d_o1 + k_o2 d_o2 + k_o3 d_o3 + k_o4 d_o4 = 2,03

Ora si possono posizionare il centro di massa ed il centro delle rigidezze all’interno del sistema di riferimento in cui si è disegnato l’impalcato.

 

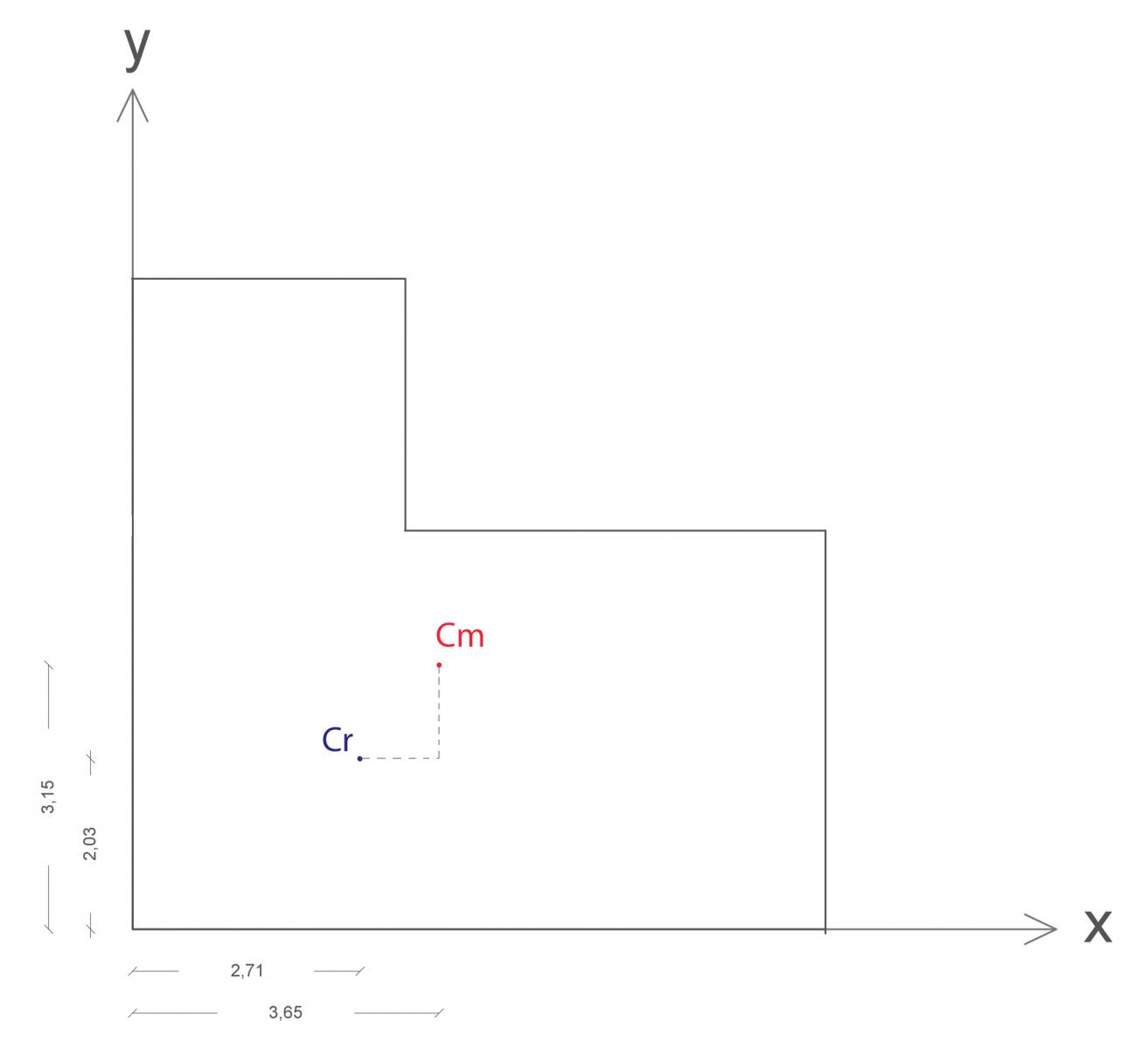
Come si nota dall’ immagine, i due punti in questo caso non coincidono. Dunque, applicando una forza in direzione orizzontale o verticale nel centro di massa dell’impalcato, oltre alla traslazione si verificherà una rotazione indotta dal momento prodotto dalla forza esterna rispetto al centro delle rigidezze.

Calcolando tutte le distanze dei controventi dal centro delle rigidezze, è possibile ricavare anche il valore della rigidezza torsionale:

k_{j =} k_v1 dd²_v1 + k_v2 dd²_v2 + k_v3 dd²_v3 + k_o1 dd²_o1 + k_o2 dd²_o2 + k_o3 dd²_o3 + k_o4 dd²_o4­ = 87336281211,66

Ora bisogna effettuare l’analisi dei carichi sismici per ricavare la forza sismica che agisce nel centro di massa, considerando i carichi strutturali, permanenti ed accidentali di un solaio in cls armato di una civile abitazione.

 

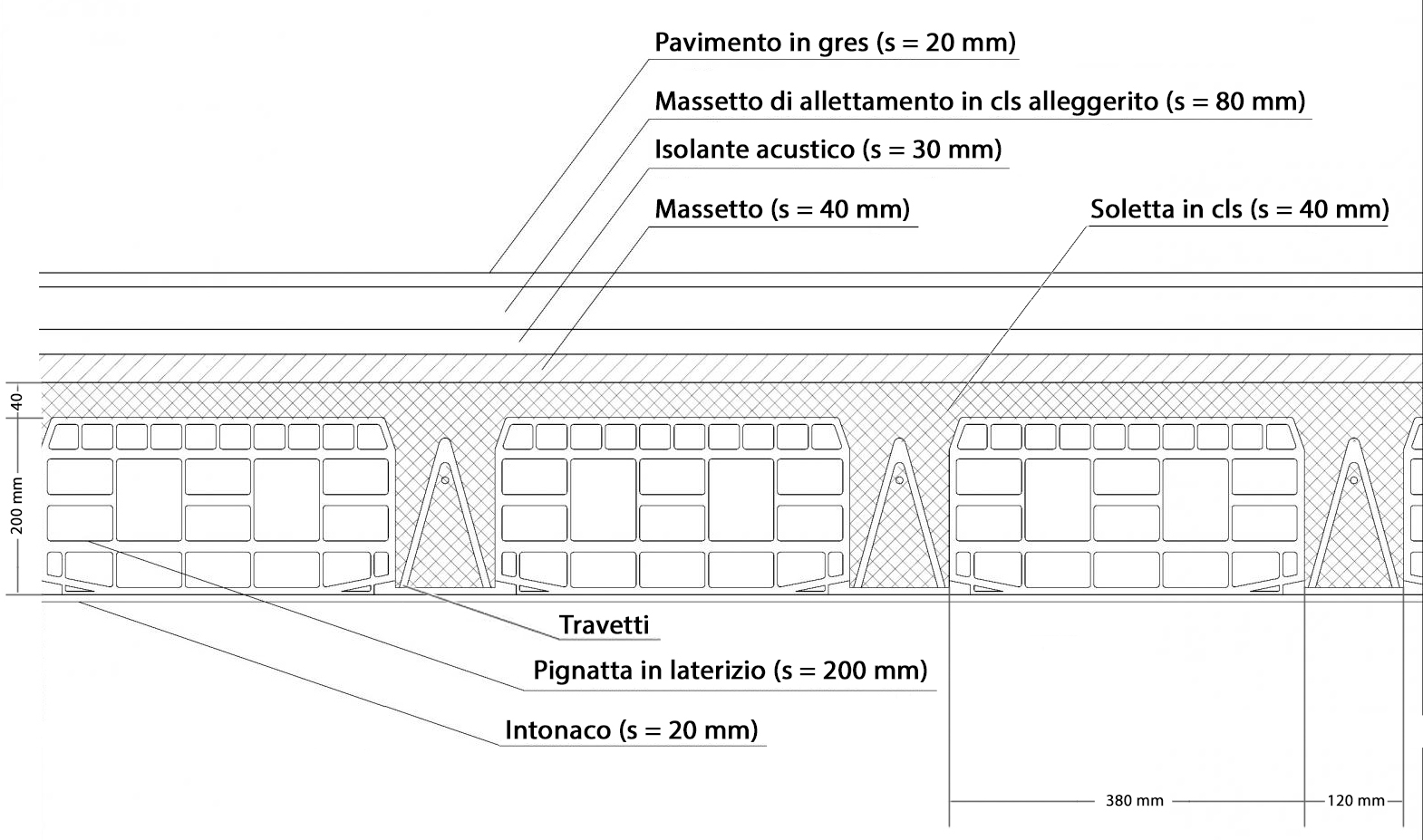
CARICHI STRUTTURALI

 

• Soletta in cls -->  γ = 25,00 KN/mc

                                       s = 40 mm = 0,04 m

                                       p.p. =  25 x 0,04 = 1 KN/mq

 

• Travetti -->  γ = 25,00 KN/mc

                              Smedio = 0,12 x 0,2 / 0,50 = 0,048 m

                              p.p. =  25 x 0,048 = 1,20 KN/mq

 

• Pignatte -->  γ = 8,00 KN/mc

                               Smedio = 0,38 x 0,2 / 0,50 = 0,152 m

                               p.p. =  8 x 0,152 = 1,22 KN/mq

 

TOTALE CARICHI STRUTTURALI = 3,42 KN/mq

 

CARICHI PERMANENTI

• Pavimento in gres (s = 20 mm)  à p.p. =0,40 KN/mq
• Massetto di allettamento in cls alleggerito --> γ=20,00 KN/mc

                                                                                    s = 80 mm = 0,08 m

                                                                                    p.p. =  20 x 0,08 = 1,6 KN/mq 

• Isolante acustico (s = 30 mm) --> p.p. =0,30 KN/mq
• Massetto in malta di cemento -->  γ = 25,00 KN/mc

                                                                  s = 40 mm = 0,04 m

                                                                 p.p. =  25 x 0,04 = 1 KN/mq 

• Intonaco (s = 20 mm)  --> γ = 18,00 KN/mc

                                                     s = 20 mm = 0,02 m

                                                     p.p. =18 x 0,02 = 0,36 KN/mq

• Incidenza impianti --> 0,5 KN/mq
• Incidenza tramezzi --> 1,60 KN/mq

TOTALE CARICHI PERMANENTI = 5,76 KN/mq

 

CARICHI ACCIDENTALI

• Cat. A _ Civile abitazione à 2 KN/mq

 

Vengono calcolati il carico totale permanente G ed il carico totale accidentale Q a partire dal valore dei carichi per unità di superficie [kN/mq].

G = (q_s + q_p) A_tot = 446,15 kN

Q = q_a A_tot = 97,20 kN

In accordo con le norme tecniche per le costruzioni (NTC2008), utilizziamo la combinazione sismica per calcolare i pesi sismici.

W = G + y_2j Q = 475,31 kN                        y_2j = coeff. di contemporaneità indicato dalla norma

Il peso sismico W rappresenta la forza peso dell’edificio, data dal prodotto tra la massa dell’edificio e l’accelerazione di gravità. Dato che il sisma  produce un’accelerazione mediamente più piccola dell’accelerazione di gravità, si introduce un coefficiente di intensità sismica cche tiene conto della sismicità del luogo di progettazione dell’edificio.

F = W c =  47,53 kN

Infine è necessario ripartire la forza sismica sui controventi ed i relativi effetti dinamici sull’ impalcato in termini di traslazione e di rotazione rigida.

Si considerano 2 casi:

1_ Forza sismica agente in direzione x, traslazione orizzontale e rotazione rigida;

2_ Forza sismica agente in direzione y, traslazione verticale e rotazione rigida.

 

Spostamento orizzontale -->  u = F / k_o,tot

Spostamento verticale --> v = F / k_v,tot

Rotazione --> j = M / k_j                           

Determinati i valori dei gradi di libertà è possibile ricavare la forza sui singoli controventi nei due casi di carico.

1 _ F // x

 Controventi orizzontali --> F_{o_n} = k_{o_n} (u + j dd_{o_n})

 Controventi verticali --> F_{v_n} = k_{v_n}  j dd_{v_n}

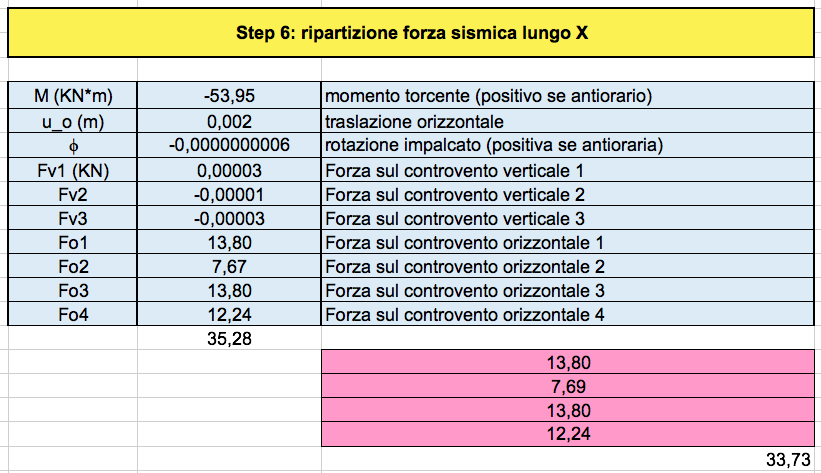
2_ F // y

Controventi verticali --> F_{v_n} = k_{v_n} (v +  j dd_{v_n})

Controventi orizzontali --> F_{o_n} = k_{o_n}  j dd_{o_n}

cari ragazzi e ragazze, con l'aiuto del vostro collega Tommaso ho stilato il seguente programma.. e' in allegato. Mi raccomando soprattutto di andarvi a rivedere l'introduzione al corso..

intelligenti pauca..

buon lavoro
la prof

 

 

 

 

INTRODUZIONE:

In questa esercitazione vedremo come si ripartisce una forza orizzontale (di natura sismica o atmosferica) sui telai che compongono la struttura intelaiata, che in questa esercitazione sarà di un solo piano.

Il sistema trave-pilastro permette, oltre che trasmettere i carichi verticali alle fondazioni, di sopportare le forze orizzontali rendendo i sistemi pilastro-trave dei controventi. La struttura esaminata sarà in cemento armato, e la tipologia dei controventi è chiamata telaio SHEAR-TYPE, che presenta tutti nodi all'incastro e la trave è ipotizzata infinitamente rigida a flessione rispetto ai pilastri, che vengono dotati di rigidezza k.

N.B.: Affinchè un sistema di controventamento sia efficace, gli impalcati vengono considerati corpi rigidi sul proprio piano (mentre al di fuori si inflettono) perciò i controventi reagiscono alla forza orizzontale che tende a spostarli, con la loro elasticità, ciò impone che un controvento, nel piano impalcato, sia un appoggio cedevole elasticamente.

Nella figura sopra è rappresentato un telaio shear-type a due ritti, dove la forza F sposta il traverso, che di conseguenza trascina con se i pilastri (si comportano come una trave doppiamente appoggiata). Il legame tra F e sigma (spostamento) è esplicitato nella formula F= [(12EI₁/h³) + (12EI₂/h³)]sigma (valevole per un telaio shear-type a due piedritti), dalla quale si ricava che k (rigidezza traslante di ogni pilastro)=12EI/h³,poichè F=k*sigma. Nel caso generale:

Grazie a questa esercitazione saremo in grado di determinare la reazione elastica di ogni controvento che sarà uguale ed opposta alla forza orizzontale che ogni singolo controvento è chiamato a ricevere attraverso il solaio (secondo il principio di azione-reazione).

DISEGNO:

Telai // all'asse y

Telaio 1v pilastri 1-5-9 ; Telaio 2v pilastri 2-6-10 ; Telaio 3v pilastri 3-7 ; Telaio 4v pilastri 4-8

Telai // all'asse x

Telaio 1o pilastri 1-2-3-4 ; Telaio 2o pilastri 5-6-7-8 ; Telaio 3o pilastri 9-10

Trattandosi di vincoli cedevoli elasticamente, i controventi vengono assimilati a molle.

DIMENSIONAMENTO:

Apro il file Excel, inserisco i dati di cui dispongo:

E=Modulo Elastico di Young (in Mpa o N/mm²); per cls con classe di resistenza C20/25

H=altezza dei pilastri (nel mio caso 3,5 m)

I=momento di inerzia di ciascun pilastro (calcolato lungo le due direzioni principali) che collabora alla formazione di ogni telaio.

Momento d'inerzia dei pilastri:

Pilastro m 0,5*0,3                     b=30 cm      h=50 cm       I_x= bh³/12 = 312500 cm4            I_y= hb³/12 = 112500 cm⁴                                                      

Inserisco i risultati nei calcoli e ottengo la rigidezza traslante dei miei 7 telai.

Nella seconda tabella riassumo le rigidezze dei controventi e inseriamo la distanza  dei rispettivi controventi dal punto di origine del sistema di riferimento da me adottato.

Nella terza tabella calcolo il centro di massa dell'impalcato, suddividendo l'area in forme geometriche  semplice delle quali mi ricaverò i singoli centri d'area.

Una volta trovate le coordinate rispetto a O dei singoli centri di massa, il file Excell mi calcola l'area totale dell'impalcato e il centro di massa totale grazie alle formule:

N.B. Le formule adottate si riferiscono ad un impalcato la quale densità sia omogenea su tutta l'area, trovandomi così sia il centro d'area che quello di massa, poichè coincidenti. Se la densità non fosse omogenea le formule adottate non sarebbero più valide.

Nella quarta tabella troviamo:

K_o=rigidezza totale orizzontale (somma delle rigidezze dei singoli controventi orizzontali)

K_v=rigidezza totale verticale (somma delle rigidezze dei singoli controventi verticali)

X_c e Y_c=coordinate dei centri di rigidezze dell'impalcato

K_phi=rigidezza torsionale totale.

Il centro delle rigidezze viene calcolato con la somma delle combinazioni tra le rigidezze e le rispettive distanze dal punto di origine. il tutto diviso per la rigidezza totale.

N.B.: La forza sismica deve essere applicata nel centro di massa G.

Dopodichè, posiziono i punti G e C (centro delle rigidezze) nello schema del mio impalcato, potendo così intuire se esso sarà soggetto solo a traslazione o anche a rotazione, ciò dipenderà dalla coincidenza o meno dei due punti.

In questo caso C e G non coincidono, anche se per poco, perciò in presenza di una forza orizzontale l'impalcato sarà soggetto sia a traslazione che a una rotzione, quest'ultima dovuta al braccio tra forza e centro delle rigidezze, creando un momento.

Con la quinta tabella effettuo l’analisi dei carichi sismici per ricavare la forza sismica che agisce nel centro di massa.

Riprendo i valori ottenuti nell'esercitazione per il dimensionamento della trave.

A partire da questi valori, il file calcola:

• G= il carico totale permanente, dato dal prodotto fra l’area totale e la somma dei carichi strutturali e permanenti
• Q= il carico totale accidentale, dato dal prodotta fra l’area totale e il carico accidentale
• W= Peso sismico o forza peso, calcolato attraverso la combinazione sismica, che richiede l’uso di ψ*²
• F= Forza sismica, data dal prodotta fra il peso sismico e c (coefficiente di intensità sismica in base alla localizzazione dell’edificio)

*² trattasi di un coefficiente di contemporaneità che tiene conto della funzione/categoria dell’impalcato; nel mio caso ho preso il valore riferito agli ambienti ad uso residenziale.

Le ultime due tabelle indicano come si ripartisce la forza sismica ai vari controventi, a seconda che essa agisca lungo l’asse x o l’asse y, e gli effetti cinematici (traslazione e rotazione rigida) sull’impalcato.

La sesta tabella ricava la forza sismica agente lungo X, la quale causa una traslazione orizzontale u ed una rotazione ϕ.

Il file di calcolo elabora i seguenti dati:

• M= momento torcente dato dalla formula F ^. (Y_c - Y_g)*³
• U_o= traslazione orizzontale dove u=F/ k_{o_tot}
• ϕ= rotazione cui è sottoposto l’impalcato; vale f= M/k_ϕ *⁴

*³ Nel mio caso è un valore positivo, quindi implica un momento antiorario.

*⁴ k_ϕ  è la rigidezza torsionale totale ricavata nella tabella 4.

La settima tabella ricava, invece, la forza sismica agente lungo Y, la quale, a sua volta, causa una traslazione verticale u ed una rotazione ϕ.

Nella tabella successiva, viene ripetuto lo stesso ragionamento, considerando la traslazione verticale:

• U_v= traslazione verticale dove u=F/ k_{v_tot}

Una volta determinati i valori dei gradi di libertà, posso ricavare la forza agente sui singoli controventi nei due casi di carico (verticale e orizzontale).

Noti u_{_o}, v_{_o}, ϕ, posso determinare le reazioni elastiche di ogni controvento attraverso le seguenti formule:

CASO 1 – Forza // all’asse X

• Fo_n=ko_n(u+ϕ∙ddo_n)       per i controventi orizzontali
• Fv_n=kv_n∙ϕ∙ddv_n            per i controventi verticali

CASO 2 – Forza // all’asse Y

• Fv_n=kv_n(v+ϕ∙ddv_n)       per i controventi verticali
• Fo_n=ko_n∙ϕ∙ddo_n            per i controventi orizzontali

Come già detto, si considera la forza nel piano dell’impalcato prima agente in direzione orizzontale e poi agente in direzione verticale; perciò analizziamo i due casi.

 

L’esercitaione prevede il dimensionamento di una travea sbalzo di un impalcato strutturale a telaio nella tre diverse teconologie: C.A., ACCIAIO E LEGNO.

Nella figura è rappresentato un impalcato strutturale 

Procedo con l’analisi dei carichi qs, qp , qa per ciascuna tecnologia:          

 

1) Dimensionamento di una trave a sbalzo in legno.

1.Sovraccarico strutturale qs

-travetto in legno: 2x (0,25*0,4)mq x 6KN/mc= 1,2 KN/mq

-tavolato: (0,03+*1*1)mq  x 6KN/mc = 0,18 KN/mq

Tot.  qs 1,38 KN/mq

2.Sovraccarico permanente qp

-piastrelle in ceramica: 0,01 x 0,2kN/mq = 0,002 KN/mq

-malta di allettamento: 0,02 x 20KN/mq = 0,4 KN/mq

-isolante: 0,04 x 1KN/mq = 0,04 KN/mq

-massetto: 0,08 x 18KN/mq = 1,44 KN/mq

 -Incidenza tramezzi 1 KN/mq  

 -incidenza impianti 0,5 KN/mq

 Tot. qp 3,382 KN/mq

3.Sovraccarico accidentale

 Da normativa per edifici a uso residenziale 2 KN/mq

4.Ora andiamo ad inserire i dati nella tabella excel  inserendo i qs, qp , qa e mi trovo il qu.                                     Inserisco la il valore della luce della trave per trovare quanto vale il Mmax.

5.Ho scelto il legno lamellare. Inserisco la tensione caratteristica a flessione fmk del legno che equivale a 24 MPa. La normativa mi fornisce la tensione di progetto fmd attraverso il coefficiente diminutivo dei valori di resistenza del materiale kmod = 0,80  ed il coefficiente parziale di sicurezza γm = 1,45 in base al materiale da me scelto. Trovo il valore della tensione di progetto fd.

6.Fisso la base b della trave per trovare hmin della sezione. Scelgo il valore di H che deve essere maggiore di hmin.

7.Dopo aver dimensionato la trave devo controllare l'abbassamento v_max e  verificare  che il rapporto tra la luce della mensola ed il suo spostamento sia  l/v_max >250 come imposto dalla normativa.

 

2) Dimensionamento di una trave a sbalzo in acciaio.

Visto che non era stato possibile pubblicare l'esercizitazione direttamente sul portale, si può trovare il file pdf con la presentazione in allegato.

L'esercitazione consiste nel dimensionamento delle travi a sbalzo di un solaio arbitrario.

Il dimensionamento delle travi è calcolato nelle tre differenti tipologie di solaio: Legno, Acciaio e Calcestruzzo armato.

L'altezza ammissibile della trave sollecitata sarà determinata come nell'esercitazione precedente, però successivamente sarà necessario effettuare la verifica a deformabilità, controllando l'abbassamento massimo dell'elemento strutturale in relazione alla sua luce.

Legno

1_Individuare nel solaio la trave a sbalzo più sollecitata e riferirsi ad essa per il dimensionamento. Nel caso ipotizzato l'interasse è di 4m, con una luce di 2,5m. Dunque ha un'area di influenza è di 10 m²

Analizzare i carichi che deve portare la struttura Qs, Qp, Qa, calcolare il momento massimo, tenendo in conto che lo schema strutturale di riferimento è quello della mensola. Nella sezione d'incastro si avrà il momento massimo che corrisponde a: M_max = qu x l²/2 = 76,11 KNm

Successivamente trovare l'altezza minima che sopporta la tensione di progetto e di conseguenza ingegnerizzarla, trovando così il profilo della trave 30cmx35cm

2_Effettuare la verifica a deformabilità della trave. Si controllerà che non vi siano spostamenti e deformazioni che possano compromettere l'efficienza della costruzione. Per questo i carichi che incidono sulla struttura sono calcolati seguendo la combinazione per gli stati limite di esercizio reversibili.

Qe = (qs + qp + 0,5qa) x 4 (interasse)= 14 kN/m

Per calcolare l'abbassamento massimo inserire nella tabella il modulo elastico E e il momento d'inerzia I_x

v_max = qe l⁴/ 8E I_x

Affinchè la sezione della trave sia verificata, il rapporto tra la luce della trave e il suo spostamento massimo deve essere maggiore di 250, come imposto dalla normativa in base al tipo di elemento strutturale considerato. L/v_max > 250

Acciaio

1_Individuare nel solaio la trave a sbalzo più sollecitata e riferirsi ad essa per il dimensionamento. Nel caso ipotizzato l'interasse è di 4m, con una luce di 2,5m. Dunque ha un'area di influenza è di 10 m²

Analizzare i carichi che deve portare la struttura Qs, Qp, Qa, calcolare il momento massimo, tenendo in conto che lo schema strutturale di riferimento è quello della mensola. Nella sezione d'incastro si avrà il momento massimo che corrisponde a: M_max =qu x l²/2 = 111,5 KNm

Successivamente trovare il modulo di resistenza a flessione minimo W_x che sopporta la tensione di progetto e di conseguenza ingegnerizzare la sezione, trovando così il profilo della trave IPE 300 con I_x 12,46 cm⁴ e peso proprio 0,422 KN/m.

2_Effettuare la verifica a deformabilità della trave. Si controllerà che non vi siano spostamenti e deformazioni che possano compromettere l'efficienza della costruzione. Per questo i carichi che incidono sulla struttura sono calcolati seguendo la combinazione per gli stati limite di esercizio reversibili.

Qe = (qs + qp + 0,5qa) x 4 (interasse) + peso trave = 21 kN/m

Nel caso dell'acciaio è stato aggiunto anche il peso proprio della trave, che a confronto con il legno ha un contributo significativo.

Per calcolare l'abbassamento massimo inserire nella tabella il modulo elastico E e il momento d'inerzia I_x

v_max = qe l⁴/ 8E I_x

Affinchè la sezione della trave sia verificata, il rapporto tra la luce della trave e il suo spostamento massimo deve essere maggiore di 250, come imposto dalla normativa in base al tipo di elemento strutturale considerato. L/v_max > 250

Calcestruzzo armato

1_Individuare nel solaio la trave a sbalzo più sollecitata e riferirsi ad essa per il dimensionamento. Nel caso ipotizzato l'interasse è di 4m, con una luce di 2,5m. Dunque ha un'area di influenza è di 10 m²

Analizzare i carichi che deve portare la struttura Qs, Qp, Qa, calcolare il momento massimo, tenendo in conto che lo schema strutturale di riferimento è quello della mensola. Nella sezione d'incastro si avrà il momento massimo che corrisponde a: M_max =qu x l²/2 = 139,16 Knm

Successivamente trovare l'altezza minima che sopporta la tensione di progetto e di conseguenza ingegnerizzarla, trovando così la sezione della trave 30cmx40cm che però dovrà essere verificata allo stato limite ultimo ovvero, considerando anche il suo peso proprio.

2_Dopo aver ottenuto la dimensione corretta della trave, effettuare la verifica a deformabilità. Si controllerà che non vi siano spostamenti e deformazioni che possano compromettere l'efficienza della costruzione. Per questo i carichi che incidono sulla struttura sono calcolati seguendo la combinazione per gli stati limite di esercizio reversibili.

Qe = (qs + qp + 0,5qa) x 4 (interasse) + peso trave = 30,3 KN/m

Per calcolare l'abbassamento massimo inserire nella tabella il modulo elastico E e il momento d'inerzia I_x

v_max = qe l⁴/ 8E I_x

Affinchè la sezione della trave sia verificata, il rapporto tra la luce della trave e il suo spostamento massimo deve essere maggiore di 250, come imposto dalla normativa in base al tipo di elemento strutturale considerato. L/v_max > 250