Blog

Per fare il dimensionamento e la verifica a deformabilità delle due travi a sbalzo indicate nel disegno, innanzitutto determino le aree di influenza. La luce è uguale a 8,2 m per tutte e due, invece gli interassi sono 1,49 m e 1,71m. Supponiamo che si tratti di un edificio ad uso residenziale.

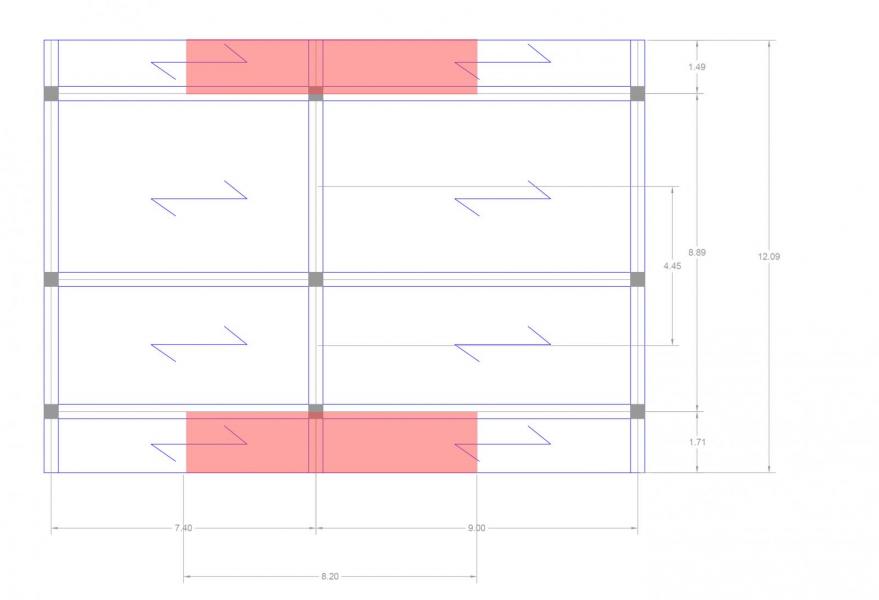
Metto i dati relativi alle travi nelle tabelle excel per i tre materiali per calcolare le sezioni minime necessarie, per poi ingegnerizzarle e fare la verifica. Per semplicità userò gli stessi solai dell'esercitazione 2 in legno, acciaio e cls.

 L'obiettivo è sempre dimensionare la trave e verificare che I / Vmax ( il momento d'inerzia diviso l'abbassamento massimo) non superi un 250esimo della luce. La base (b) è 40 cm per tutte e due travi. 

• LEGNO 

M max = (qu * l^2 )/ 8  - Momento massimo sulla trave
Fm,k - resistenza caratteristica a flessione da scegliere tra 24, 28, 32, 36 seguendo la normativa
Kmod - coefficiente diminutivo dei valori di resistenza del materiale (clima, umidità, durata del carico ecc) media= 0.8
γm- il coefficiente parziale di sicurezza relativo al materiale, tra 1 e 1,50.

E: modulo elastico del materiale

Peso: per il legno non viene considerato

qe: la combinazione dei carichi incidenti sulla struttura (qs + qp+ ψ11 * qa) * luce + peso 
(ψ11: 0,5) 

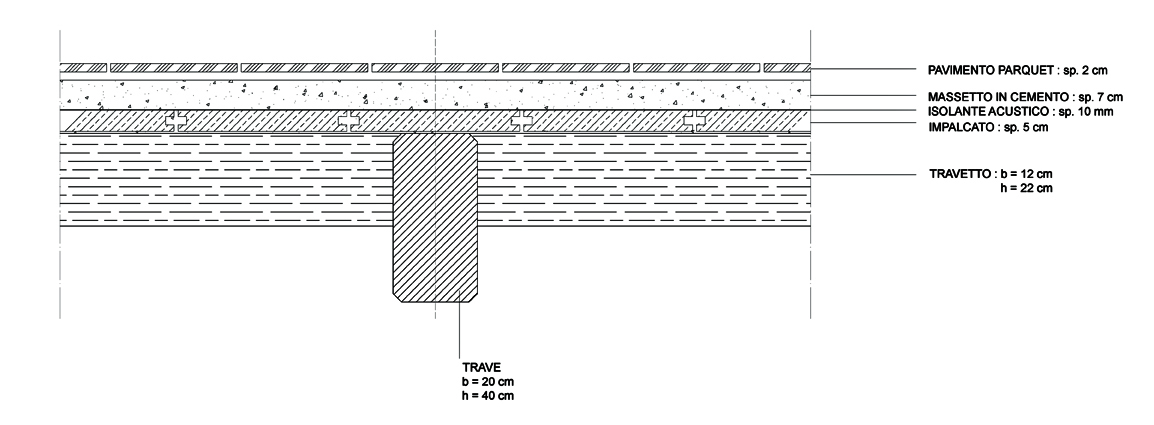
• Carichi strutturali (qs): 

Impalcato in legno di noce:                                                                                                                  

peso specifico : 600 kg/mc 
volume tavolato (per 1 mq) : 0,05 m x 1,00 m x 1 ,00 m = 0,05 mc                                              

peso tavolato (per 1 mq) : 600 kg/mc x 0,05 mc = 30 kg/mq = 0,30 kN/m

Carichi permanenti (qp) :
Massetto in cemento :                                                                                                                          

massa volumica : 2000 kg/mc                                                                                                        

volume massetto (per 1 mq) : 0,07 m x 1,00 m x 1 ,00 m = 0,07 mc                                            

peso massetto (per 1 mq) : 2000 kg/mc x 0,07 mc = 140 kg/mq = 1,40 kN/mq 

Isolante acustico : 
peso isolante (per 1 mq) : 7 kg/mq = 0,07 kN/mq
Parquet in rovere:                                                                                                                                

peso specifico : 750 kg/mc                                                                                                          

volume parquet (per 1 mq) : 0,02 m x 1,00 m x 1 ,00 m = 0,02 mc                                              

peso parquet (per 1 mq) : 750 kg/mc x 0,02 mc = 15 kg/mq = 0,15 kN/mq

Incidenza impianti: 0,5 kN/mq
Incidenza tramezzi: 1 kN/mq

• Sovraccarichi accidentali (qa): 

in ambiente residenziale: 2,0 kN/m2

CARICO TOTALE : (qs+qp+qa) x interasse
(0,30 + 3,12 + 2) x 1 = 5,42 kN/m

Hmin della prima trave viene 73,74 cm, ingegnerizzando 75 cm. 

Hmin della seconda trave viene 68,83 cm, ingegnerizzando 70 cm. 

I/vmax è minore a 1/250, quindi le travi sono verificate. 

• ACCIAIO 

Fy,k- snervamento caratteristico  che varia tra 235- 355- 375 (N/mm2)
Fyd- tensione di snervamento - Fyk / 1,05 (snervamento caratteristico diviso coefficiente parziale di sicurezza)
Wx min - resistenza a flessione minimo : Mmax / Fyd

E: modulo elastico del materiale 

Peso: per l'acciaio si trova dal profilario in kg/m e si converte in KN/m

qe: la combinazione dei carichi incidenti sulla struttura (qs + qp+ ψ11 * qa) * luce + peso 
(ψ11: 0,5) 

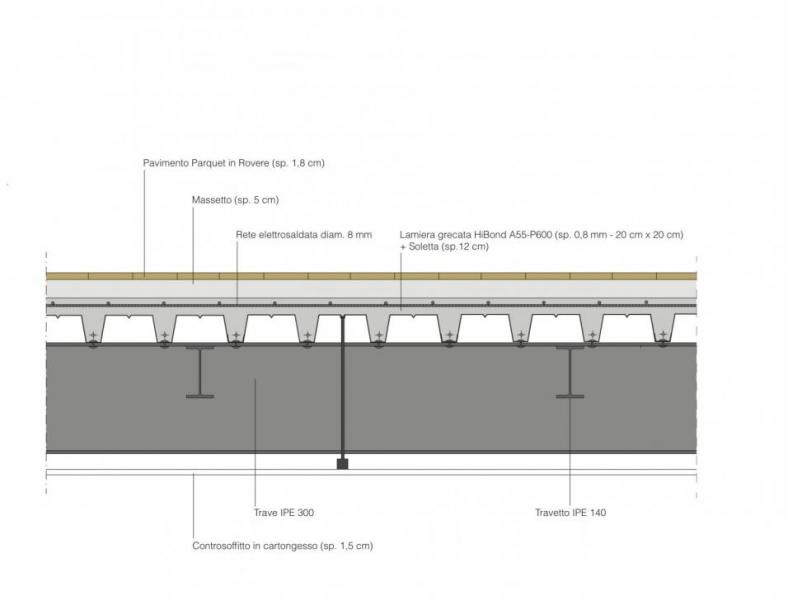
• Carichi strutturali (qs): 

Composti da : travi, travetti, lamiera grecata, soletta

Lamiera grecata mod. A55-P600-G5 HiBond (sp. 0,8 mm):
Peso al mq = 0,105 KN/mq
 
Soletta in cemento (sp. 12 cm):
 Peso Specifico = 2100  Kg/mc
Volume  al mq =  0,12 m x 1m x 1m = 0,12 mc
Peso al mq = 0,12 mc x 2100 Kg/mc = 252 Kg/mq = 2,52 KN/mq
 qs = 2,63 KN/mq
 

• Carichi permanenti (qp) : 

Composti da: pavimento in parquet, massetto, rete elettrosaldata, controsoffitto, impianti, tramezzi

Pavimento in Parquet di Rovere (sp. 1,8 cm): 
Peso Specifico = 750  Kg/mc
Volume  al mq =  0,018 m x 1m x 1m = 0,018 mc
Peso al mq = 0,018 mc x 750 Kg/mc = 13,5 Kg/mq = 0,135 KN/mq
 
Massetto (sp. 5 cm):
 Peso Specifico = 2100  Kg/mc
Volume  al mq =  0,05 m x 1m x 1m = 0,05 mc
Peso al mq = 0,02 mc x 2100 Kg/mc = 105 Kg/mq = 1,05 KN/mq
 
Rete elettrosaldata  820/2 AD (diam. 8mm; 20 cm x 20 cm) :
Peso al mq = 0,04 KN/mq
 
Controsoffitto in cartongesso (sp. 1,5 cm):
 Peso Specifico = 1325  Kg/mc
Volume  al mq =  0,015 m x 1m x 1m = 0,015 mc
Peso al mq = 0,015 mc x 1325 Kg/mc = 19,875 Kg/mq = 0,2 KN/mq
 
Incidenza Impianti:
0,5 KN/mq
 
Incidenza Tramezzi:
1 KN/mq
 
qp = 2,93 KN/mq
 

• Sovraccarichi accidentali (qa):

in ambiente residenziale: 2,0 kN/m2

CARICO TOTALE : (qs + qp + qa) x interasse = (2,63 + 2,93 + 2) KN/mq  x 1m = 7,56 KN/m

 
Scelgo di utilizzare un acciaio con valore di snervamento fy,k = 275 N/mmq e, inserendo i dati nel foglio excel, ottengo un Modulo di Resistenza Wx (Momento max/ Resistenza a flessione di progetto) pari a 2373,76 cm3 per la prima trave e 2068,36 cm3 per la seconda:
 Scelgo quindi di utilizzare un profilo IPE (55 cm x 21 cm) con Wx 2441,00 cm3 per tutte e due. Il peso di questo profilo è pari a 106 kg/m, facendo la conversione 1,03 kN/m. 

I/vmax è minore a 1/250, quindi le travi sono verificate.

• CLS ARMATO

Fck- resistenza caratteristica del cls tra 60 e 70 N/mm2.
Fyk- resistenza caratteristica dell'acciaio per l'armatura  = 450 Mpa
Fyd - la tensione del progetto dell'acciaio = Fyk/  γs ( γs: coefficiente parziale di sicurezza). 
Fcd- la tensione del progetto del cls= acc * Fck/ γc (γc: 1,5, acc: 0,85 coefficiente riduttivo per resistenza di lunga durata). 
qe: la combinazione dei carichi incidenti sulla struttura (qs + qp+ ψ11 * qa) * luce + peso 
(ψ11: 0,5) 

Peso: per cls è pari 25 kN/m3

E: modulo elastico del materiale 

• Carichi strutturali (qs): 

caldana in calcestruzzo: [(0,04*1,00*1,00)m3 + (0,16*0,20*1,00)m3]/m2 * 2300kg/m3 = 165,60 kg/m2 = 1,66 kN/m2
rete elettrosaldata (maglia 15cm*15cm  ø8): 5,3 kg/m2 = 0,053 kN/m2
travetti: 2,00ml/m2 * 10,50kg/ml = 21,00 kg/m2 = 0,21 kN/m2
pignatte : 66,4 kg/m2 = 0,66 kN/m2
totale:    qs = 2,58 kN/m2

• Carichi permanenti (qp) :

pavimento in cotto (10 pz/m2): 42,0 kg/m2 = 0,42 kN/m2
massetto in sabbia e cemento: (0,04*1,00*1,00)m3/m2 * 1800kg/m3 = 72,0 kg/m2 = 0,72 kN/m2
isolamento acustico: 5 kg/m2 = 0,05 kN/m2
intonaco: 13,3kg/m2 = 0,13 kN/m2
incidenza tramezzi: 0,5 kN/m2
incidenza impianti: 1,0 kN/m2
totale:    qp = 2,82 kN/m2

• Sovraccarichi accidentali (qa): 

in ambiente residenziale: 2,0 kN/m2

CARICO TOTALE : (qs+qp+qa) x interasse
(2,82 + 2,58+ 2) x 1 = 7,4 kN/m

Hmin della prima trave viene 49,15, ingegnerizzando 50 cm. 

Hmin della seconda trave viene 46,21 cm, ingegnerizzando 50 cm. 

I/vmax è minore a 1/250, quindi le travi sono verificate. 

Dopo aver disegnato un solaio a scelta selezionare la trave più sollecitata, definire il dimensionamento di essa con diverse tipologie di solaio ed eseguire le verifiche degli abbassamenti massimi.

1. DIMENSIONAMENTO DELLE MENSOLE

Come nella precedente esercitazione, per dimensionare la trave, calcolare i carichi che agiscono su di essa          (Qu= (Qs x γ_G1 + Qp x γ_G2  + Qa x γ_G3  x interasse) e calcolare il momento massimo. La trave in questo caso non è più appoggiata ma si comporta come una mensola. Quindi il momento massimo non sarà più M_max= Q_u x l²/8 ma si prenderà in considerazione per i calcoli l’espressione:

        → M_max=Q_u x l²/2

• DIMENSIONAMENTO TRAVE IN LEGNO

Scelta la tipologia di solaio e studiata la stratigrafia con un analisi dei carichi si ottiene un M_max

In seguito scegliendo una tipologia di legno (lamellare GL28h), tenendo conto di alcuni coefficienti di sicurezza e impostando una base predefinita trovare l’altezza minima della trave.Cercare su un formulario l’altezza di progetto prendendo un altezza che superi l’altezza minima.In questo caso si otterrà una trave 25x50.

• DIMENSIONAMENTO TRAVE CLS ARMATO

Scelta la tipologia di solaio e studiata la stratigrafia con un analisi dei carichi si ottiene un M_max

Essendo un materiale non omogeneo (acciaio S450 e calcestruzzo C50) calcolare le due tensioni di progetto: dell’acciaio f_yk e del calcestruzzo f_ck. In seguito definire una base e trovare un’altezza, sempre considerando un ‘altezza maggiore dell’H_min trovata. Infine verificare che il peso proprio della trave non influisca il dimensionamento iniziale con il carico Q_u. In questo caso si ottiene una trave 30x40.

• DIMENSIONAMENTO TRAVE IN ACCIAIO

Scelta la tipologia di solaio e studiata la stratigrafia con un analisi dei carichi si ottiene un M_max

In seguito scegliendo una tipologia di acciaio (acciaio S235), grazie alla tensione di progetto f_yk, trovare il modulo di resistenza a flessione minimo. Infine trovare una tipologia di IPE che abbia un Wd>Wxmin (in questo caso IPE360).

2. CALCOLO E VERIFICA ABBASSAMENTI MENSOLA

Calcolare l’abbassamento massimo di ogni mensola con la formula

        → V_max = (q_e x l⁴)/(8EI_x)

Considerando che non deve superare 1/250 della luce (che in questo caso è 4m)

        → (l/V_max)>250

• CALCOLO E VERIFICA TRAVE IN LEGNO

Applicare la combinazione di carico agli SLE per la combinazione ad uso frequente qe ed inserire il modulo di elasticità E del legno per ottenere il momento d’inerzia I_x.

       → qe= (qs + qp + ψ1j) x i = 8KN/m

       → Ix= (b x h^3)/ 12 = 260417cm⁴

Quindi calcolare l'abbassamento massimo con la formula:

       → V_max = (q_e x l⁴)/(8EI_x)= 1,20cm

e verificare come da normativa che (l/V_max)>250 →  (l/V_max)= 334>250 a questo punto l'asta è dimensionata e verificata.

• CALCOLO E VERIFICA TRAVE IN CALCESTRUZZO ARMATO

Conoscendo base e altezza calcolare l'area della sezione ( A= b x H ) e il peso di essa, moltiplicando il peso specifico del materiale per l'area della sezione.Nel calcestruzzo deve essere considerato nel calcolo anche il peso proprio della trave poichè è un materiale molto pesante e potrebbe influire con i calcoli del dimensionamento e della verifica.

Applicare la combinazione di carico agli SLE per la combinazione ad uso frequente qe ed inserire il modulo di elasticità E per ottenerei il momento d’inerzia I_x.

       → qe=(qs + qp + ψ1j) x i + peso = 15.44Kn/m

       → Ix= (b x h^3)/ 12 = 160000cm⁴

Quindi calcolare l'abbassamento massimo con la formula:

       → V_max = (q_e x l⁴)/(8EI_x)= 1,47cm

e verificare come da normativa che (l/V_max)>250 →  (l/V_max)=272>250 a questo punto l'asta è dimensionata e verificata.

• CALCOLO E VERIFICA TRAVE IN ACCIAIO

Applicare la combinazione di carico agli SLE per la combinazione ad uso frequente qe (considerando il peso della trave) ed inserire il modulo di elasticità E e il momento d’inerzia Ix. Nel caso della trave in acciaio non è necessario calcolare il momento d'inerzia poichè è tabellato: trovato Wx si sceglie una IPE e si trova un momento d'inerzia predefinito.

       → qe=(qs + qp + ψ1j) x i + peso =12.451Kn/m

Quindi calcolare l'abbassamento massimo con la formula:

       → V_max = (q_e x l⁴)/(8EI_x)= 1.166cm

e verificare come da normativa che (l/V_max)>250 →  (l/V_max)=343>250 a questo punto l'asta è dimensionata e verificata.

La terza esercitazione consiste nel dimensionamento di una mensola considerando le tre principali tecnologie, ossia acciaio, legno e calcestruzzo, e nella verifica dell’abbassamento verticale massimo v_max. Il rapporto tra la luce e l'abbassamento deve essere minore di 1/250 della luce in esame.

Come prima cosa è necessario disegnare l’impalcato strutturale di un solaio (travi principali, secondarie e travetti) e individuare la mensola con la maggiore area di influenza –a parità di area di influenza consideriamo la trave con la luce maggiore-.

In questo caso abbiamo una trave di luce 2,5m e un interasse di 3,5m, pertanto l’area di influenza è di 8,75m².

Dimensioniamo la mensola utilizzando lo stesso procedimento utilizzato nella precedente esercitazione, tuttavia in questo caso il momento (non essendo una trave biappoggiata) sarà M_max = q_ul²/2.

SOLAIO IN ACCIAIO

• Peso proprio strutturale (qs) =  1,47 kN/m²
• Carico permanente (qp) = 2,69 kN/m²
• Carico accidentale (qa) = 4kN/m² (per normativa)

A questo punto è possibile inserire i dati ottenuti per il dimensionamento della trave all’interno del foglio Excel (compresi luce e interasse) in modo da ottenere la combinazione a stato limite ultimo q_u, il momento Mmax e il modulo di resistenza W_xmin.

Si ottiene una trave IPE 300

Verifichiamo ora l’abbassamento verticale

V_max = q_el⁴/8EI_x             l/v_max > 250

In cui qe è lo SLE q_e= (q_s+ q_p+ psi₁₁ x q_a) x i

SOLAIO IN LEGNO

• Peso proprio strutturale (qs) =  0,29 kN/m²
• Carico permanente (qp) = 2,69 kN/m²
• Carico accidentale (qa) = 4kN/m² (per normativa)

A questo punto è possibile inserire i dati ottenuti per il dimensionamento della trave all’interno del foglio Excel (compresi luce e interasse) in modo da ottenere la combinazione a stato limite ultimo q_u, il momento Mmax e la resistenza di progetto f_d.

Da questo valore, fissando una base si determina l’altezza minima che la sezione della trave deve avere.

Si ottiene una trave in legno di 30x50 cm

Verifichiamo ora l’abbassamento verticale

SOLAIO IN LATEROCEMENTO

• Peso proprio strutturale (qs) =  3 kN/m²
• Carico permanente (qp) = 2,69 kN/m²
• Carico accidentale (qa) = 4kN/m² (per normativa)

A questo punto è possibile inserire i dati ottenuti per il dimensionamento della trave all’interno del foglio Excel (compresi luce e interasse) in modo da ottenere la combinazione a stato limite ultimo q_u, il momento Mmax e la resistenza di progetto sia dell’acciaio che compone l’armatura sia del calcestruzzo.

Da questo valore, fissando una base si determina l’altezza minima che la sezione della trave deve avere fino al centro delle aree dell’armatura, a cui bisogna aggiungere un certo delta che rappresenta la distanza tra il centro delle aree dell’armatura e la “fibra” maggiormente tesa.

Verifichiamo ora l’abbassamento verticale

La geometria che utilizzerò per il dimensionamento della mensola, nelle tre tecnologie: cls armato, acciaio e legno è la seguente

La trave maggiormente sollecitata ha una luce di 1,5m e un interasse di 5m

MENSOLA IN CLS ARMATO

Definisco la stratigrafia del mio solaio, in questo caso latero cementizio, e calcolo tutti i carichi che vi gravano, come nella precedente esercitazione.

Carico strutturale (qs)

- soletta collaborante :                      (0,04m x 1m x 1m)/mq x 24KN/mc = 0,96 KN/mq
- travetti:                                        2(0,10m x 0,16m x 1m)/mq x 24KN/mc = 0,768 KN/mq
- pignatta:                                       8 x 9,1 Kg/mq = 72,8 Kg/mq = 0,728 KN/mq

Q_s = (0,96 + 0,768 + 0,728 ) KN/mq = 2,456 KN/mq

Carico permanente (qp)

- pavimento in cotto:                        24Kg/mq = 0,24KN/mq
- malta di sottofondo:                       (0,02m x 1m x 1m)/mq x 18KN/mc = 0,36KN/mq
- strato di allettamento in cls             (0,03m x 1m x 1m)/mq x 24KN/mc= 0,72KN/mq
- isolante in lana di vetro                  (0,08m x 1m x 1m)/mq x 0,2KN/mc = 0,016KN/mq
- massetto delle pendenze                 (0,04m x 1m x 1m)/mq x 18KN/mc = 0,72KN/mq intonaco                                       (0,01m x 1m x 1m)/mq x 13KN/mc = 0,13KN/mq

Q_p= (0,24 + 0,36 + 0,72 + 0,016 + 0,72 + 0,13 ) KN/mq = 2,186 KN/mq

Carico accidentale (qa)

Anche qui ho ipotizzato un uso residenziale, seguendo la tabella della normativa quindi ho:

Qa = 2 KN/mq

Dopo aver inserito nel file anche la luce, viene calcolato automaticamente il Mmax agente sulla trave.

In seguito imposto le proprietà sia dell’acciaio (fyk) che del calcestruzzo (fck) che vengono automaticamente moltiplicati per i loro coefficienti di sicurezza (1,15 e 1,5).

Essendo la trave composta da due materiali diversi, le proprietà del materiale devono essere omogenizzate secondo un coefficiente (n=15) in modo da ottenere ß e r. 

Ora posso impostare la larghezza della trave (b=40 cm) così che Excel mi calcola l’altezza utile della trave (Hu=21,38), che sommata alla distanza dal baricentro del ferro teso al lembo teso (δ=4) e mi da l’altezza minima(Hmin=25,38). 

Ingegnerizzo scegliendo una sezione alta 30 cm.

A questo punto è possibile ottenere il peso unitario della trave e il Qe;

Automaticamente quindi Excel svolge un’altra volta tutta la riga con i nuovi dati (è cambiato il qu) così posso sapere se la trave progettata è verificata o meno.

È verificata

Il procedimento per il dimensionamento della mensola è molto simile a quello per la trave doppiamente appoggiata, ma in più anche per il cemento armato sarà necessario fare la verifica ad abbassamento dove Vmax=qel^4/8EIx e l/ Vmax ≥ 250

MENSOLA IN ACCIAIO

Carico strutturale (qs)

- IPE 200: 2 (0,00285 mq x 1 m) / 78,5 KN/mc = 0,447 KN/mq

- Getto in calcestruzzo e lamiera grecata: (21 kN/mc x 0,075 mc) / 1 mq = 1,86 KN/mq

Qs = 0,447 kN/mq + 1,86 kN/mq = 2,307 kN/mq

Carico permanente (qp)

-pavimento, 0,3 KN/mq

-massetto, (0,03 m x 1 m x 1 m) /mq x 19 KN/mc = 0,57 KN/mq

-isolante, (0,06 m x 1 m x 1 m) /mq x 14 Kn/mc = 0,84 KN/mq

Qp = 0,3 KN/mq +  0,57 KN/mq + 0,84 KN/mq = 1,71 KN/mq

Carico accidentale (qa)

Anche qui ho ipotizzato un uso residenziale, seguendo la tabella della normativa quindi ho:

Qa = 2 KN/mq

Compilo il foglio Excel con i tre carichi così da calcolare il qu.

In seguito aggiungo la luce della trave (3m) così da ottenere il M_max (M =ql^2/2)

Aggiungo le caratteristiche del materiale fyk che verrà moltiplicato per il coefficiente di sicurezza γ=1,05 per ottenere il Wxmin (215,24).

Dato Wxmin, scelgo sul sagomario un'IPE 220 e di conseguenza inserisco il valore del momento di inerzia in tabella Ix=2772cm^4

Con questi ultimi dati posso verificare se la sezione scelta rispetta i limiti di abbassamento. Il foglio infatti mi calcolerà il Qe (che in questo caso tiene in considerazione anche il peso della trave, a differenza del legno che è considerato un materiale leggero ), con cui sarà possibile calcolare l'abbassamento max (Vmax) e verificare che il rapporto tra la luce della trave e il suo spostamento max sia maggiore di 250, come da normativa.

Vmax=qel^4/8EIx                                 l/ Vmax ≥ 250

la sezione è verificata ed idonea

MENSOLA IN LEGNO

Carico strutturale (qs)

-tavolato, (0,03 m x 1 m x 1 m) /mq x 7 KN/mc = 0,21 KN/mq

-travetti, 2(0,1 m x 0,14 m x1 m) /mq 6 KN/mq = 0,168 KN/mq

Qs = 0,21 KN/mq + 0,168 KN/mq = 0,378 KN/mq

Carico portato (qp)

-pavimento, 0,3 KN/mq

-massetto, (0,03 m x 1 m x 1 m) /mq x 19 KN/mc = 0,57 KN/mq

-allettamento, (0,06 m x 1 m x 1 m) /mq x 14 Kn/mc = 0,84 KN/mq

Qp = 0,3 KN/mq + 0,57 KN/mq + 0,84 KN/mq = 1,71 KN/mq

Carico accidentale (qa)

Prendendo la tabella dalla normativa ho ipotizzato un uso residenziale quindi ho:

Qa = 2 KN/mq

Compilo il foglio Excel con i tre carichi così da calcolare il qu, che è la somma dei tre carichi moltiplicati per dei coefficienti di sicurezza x l’interasse.

In seguito posso aggiungere la luce della trave, in modo da ottenere il M_max.

Fino a questo punto il l’iter di progetto utilizzato è lo stesso per quella della trave doppiamente appoggiata, ma il M_max è differente poiché dobbiamo far riferimento al modello di mensola, quindi

M =ql^2/2 

Inserisco i dati relativi al tipo di legno scelto per la trave da progettare.

Imposto una base di 30 cm ottenendo una H_min pari a 20,14.

Ingegnerizzo questa misura prendendo H = 25 cm

Per la mensola è necessario calcolare e verificare l’abbassamento della trave.

Determino quindi il modulo elastico  (E=8000) e il momento d'inerzia (Ix=(b*h³) /12) e carico totale qe (combinazione di carico frequente per SLE reversibili), necessario per il calcolo dello spostamento.

Qe = (G1 + G2 + Ψ1 x  Q1) x i

A questo punto è possibile calcolare l'abbassamento max (Vmax) e verificare che il rapporto tra la luce della trave e il suo spostamento max sia maggiore di 250, come da normativa.

Vmax=qel^4/8EIx                                 l/ Vmax ≥ 250

E' Verificata

I calcoli riportati di seguito descrivono il dimensionamento della trave più sollecitata di un balcone ad uso residenziale con tre materiali differenti, acciaio, legno e calcestruzzo armato.

Poiché il seguente dimensionamento riprende in parte il procedimento della seconda esercitazione già pubblicata, dove necessario saranno fatti dei riferimenti alla stessa.

L’elemento preso come oggetto di studio è la mensola con area di influenza maggiore di un impalcato strutturale che rispecchia il balcone di un livello di edificio ad uso residenziale meglio descritto dagli elaborati allegati di seguito: 

Step-1: Vengono analizzate tutte le aree di influenza delle travi principali dell’impalcato strutturale per evidenziare l’elemento oggetto del dimensionamento;

LUCE = 1,50 m

AREA DI INFLUENZA = 8,60 m

Step-2: Il calcolo dei carichi strutturali (qs) e permanenti (qp) viene ripreso dalla seconda esercitazione e come descritto nella stessa, questo varierà a seconda della tecnologia dei solai che si sono scelti per il calcolo da effettuare.

Il carico accidentale (qa) differenzia dal valore di 2 KN/mq, presente nell’esercitazione precedente, poiché la normativa (D.M. 14.01.2008) definisce un differente valore di carico qa per gli ambienti suscettibili di affollamento, come nel caso che segue di un balcone che rientra in categoria C2 con valore di carico accidentale pari a:

qa = 4 KN/mq

Le tipologie tecnologiche dei solaio sono state scelte in base all’abaco dei modelli UNI10355

SOLAIO-15  PROFILATI ACCIAIO E TAVELLONI – dimensionamento in acciaio;

SOLAIO-12  SOLAIO IN LEGNO – dimensionamento in legno;

SOLAIO-04  LATERO CEMENTO CON BLOCCHI COLLABORANTI – dimensionamento in calcestruzzo armato.

ACCIAIO

Step-3 acciaio: Si procede al dimensionamento della sezione della mensola tramite lo stesso procedimento dell’esercitazione precedente, ricavandoci i dati necessari per la scelta del profilo da appositi sagomari, con la sola eccezione del calcolo del M_max poiché essendo una mensola anziché una trave doppiamente appoggiata analizzata nell’esercitazione precedente, questo M_max avrà un valore pari a ql²/2

(link esercitazione 2: http://design.rootiers.it/strutture/node/2069) 

Step-4 acciaio: Dimensionata la sezione (IPE 240) si procede alla verifica dell’abbassamento massimo (v_max), poiché essendo questo un elemento mensola, il suo abbassamento sarà oggetto di dimensionamento, così come anche il calcolo del peso proprio dell’elemento che in quanto acciaio, in questo caso, non potrà essere trascurato durante il carico di qe;

qe identifica la combinazione di carico per le analisi allo Stato Limite di Esercizio (SLE) che terranno conto dell’abbassamento da verificare:

qe = qs + qp + 0,5 * qa + peso proprio dell’elemento

ABBASSAMENTO MASSIMO: v_max

Dovendo verificare che la sezione dimensionata tramite lo stesso approccio dell’esercitazione precedente sia efficace per la verifica dell’abbassamento massimo, come prescritto da normativa, si procede con il calcolo del v_max , per poi operare con:

l/v_max > 250         come nel testo della normativa.

Per ricavare il valore di v_max si ha bisogno di effettuare i calcoli mediante il metodo della linea elastica che di seguito sarà sintetizzato per il caso dell’elemento mensola:

- si ricava il momento M_s tramite il taglio virtuale che si opera sull’elemento:

M_s = -ql²/2 + qls – qs²/2

- dall’equazione di legame costitutivo: M = EI χ si ricava la curvatura:

χ_s = -ql²/2EI + qls/EI – qs²/2EI

- integrando secondo l’equazione di congruenza χ = dϕ/ds:

ϕ_s = -ql²s/2EI + qls²/2EI – qs³/6EI + c1

- integrando ϕ_s d_s si ricava l’abbassamento in funzione di s:

v_s = -ql²s²/4EI + qls³/6EI – qs⁴/24EI + c1s + c2

poiché si deve ricavare l’abbassamento massimo, allora v_s sarà calcolato per s=l, dove “l”è la luce della mensola poiché li si avrà l’abbassamento massimo.

Quindi:

v_max = v_(l) = -ql⁴/4EI + ql⁴/6EI – ql⁴/24EI = -ql⁴/8EI = ql⁴/8EI

Step-4 acciaio: Si ricava quindi v_max = ql⁴/8EI e si confronta con il limite in normativa per verificare che la sezione sia ben dimensionata:

LEGNO

Step-3 legno: come per l’acciaio si dimensiona la sezione della mensola come nell’esercitazione precedente con l’inserimento dei dati relativi al materiale dalle tabelle riportate di seguito: 

Step-4 legno: una volta ricavati i dati relativi al dimensionamento della sezione in legno, come per l’acciaio si procede con il calcolo dell’abbassamento massimo (SLE), trascurando nel caso del legno il paso proprio della trave poiché il peso specifico di questo materiale è molto basso;

CALCESTRUZZO ARMATO

Step-4 c.a.: Si ripetono gli step analizzati precedentemente per il dimensionamento della sezione in c.a., per poi arrivare a calcolare anche per questa sezione l’abbassamento massimo v_max ;

TRAVE IN CLS ARMATO

Per il dimensionamento di una trave in cls armato, riutilizzo una carpenteria disegnata per il laboratorio di architettura tecnica fatto anni fa.

Dimensiono la trave 2 C-D

Luce: 4m

Interasse: 4m

Area di influenza : 16m

Il solaio in latero cemento:

pignatte 400x140mm e travetti da 100x140mm posti a 50cm di interasse. In un metro di solaio abbiamo perciò due pignatte e due travetti in quanto il rapporto 1/interasse, cioè 1/0,50 m= 2.

Carico strutturale (qs)

- soletta collaborante :                      (0,04m x 1m x 1m)/mq x 24KN/mc = 0,96 KN/mq
- travetti:                                        2(0,10m x 0,16m x 1m)/mq x 24KN/mc = 0,768 KN/mq
- pignatta:                                       8 x 9,1 Kg/mq = 72,8 Kg/mq = 0,728 KN/mq

Q_s = (0,96 + 0,768 + 0,728 ) KN/mq = 2,456 KN/mq

Carico permanente (qp)

- pavimento in cotto:                        24Kg/mq = 0,24KN/mq
- malta di sottofondo:                       (0,02m x 1m x 1m)/mq x 18KN/mc = 0,36KN/mq
- strato di allettamento in cls             (0,03m x 1m x 1m)/mq x 24KN/mc= 0,72KN/mq
- isolante in lana di vetro                  (0,08m x 1m x 1m)/mq x 0,2KN/mc = 0,016KN/mq
- massetto delle pendenze                 (0,04m x 1m x 1m)/mq x 18KN/mc = 0,72KN/mq                                              - -intonaco                                       (0,01m x 1m x 1m)/mq x 13KN/mc = 0,13KN/mq

Q_p= (0,24 + 0,36 + 0,72 + 0,016 + 0,72 + 0,13 ) KN/mq = 2,186 KN/mq

Carico accidentale (qa)

Ipotizzo un uso residenziale, seguendo la tabella della normativa quindi ho:

Qa = 2 KN/mq

Dopo aver inserito nel file anche la luce, viene calcolato automaticamente il Mmax agente sulla trave. In seguito imposto le proprietà sia dell’acciaio (fyk) che del calcestruzzo (fck) che vengono automaticamente moltiplicati per i loro coefficienti di sicurezza (1,15 e 1,5).

Essendo la trave composta da due materiali diversi, le proprietà del materiale devono essere omogenizzate secondo un coefficiente (n=15) in modo da ottenere ß e r.

Ora posso impostare la larghezza della trave (b=30 cm) così Excel mi calcola direttamente l’altezza utile della trave, che sommata alla distanza dal baricentro del ferro teso al lembo teso (δ=4) e mi da l’altezza minima

L’altezza minima è 24 cm, che ingegnerizzo scegliendo una sezione alta 25 cm.

E' verificata.

TRAVE IN ACCIAIO S235

Ipotizzo lo stesso schema geometrico anche per la carpenteria in acciaio e procedo con il calcolo dei carichi.

Carico strutturale (qs)

- IPE 200: 2 (0,00285 mq x 1 m) / 78,5 KN/mc = 0,447 KN/mq

- Getto in calcestruzzo e lamiera grecata: (21 kN/mc x 0,075 mc) / 1 mq = 1,86 KN/mq

Qs = 0,447 kN/mq + 1,86 kN/mq = 2,307 kN/mq

Carico permanente (qp)

-pavimento, 0,3 KN/mq

-massetto, (0,03 m x 1 m x 1 m) /mq x 19 KN/mc = 0,57 KN/mq

-isolante, (0,06 m x 1 m x 1 m) /mq x 14 Kn/mc = 0,84 KN/mq

Qp = 0,3 KN/mq +  0,57 KN/mq + 0,84 KN/mq = 1,71 KN/mq

Carico accidentale (qa)

Anche qui ho ipotizzato un uso residenziale, seguendo la tabella della normativa quindi ho:

Qa = 2 KN/mq

Compilo il foglio Excel con i tre carichi così da calcolare il qu (la somma dei tre carichi moltiplicati per dei coefficienti di sicurezza x l’interasse).

L’impalcato è lo stesso che ho utilizzato per il dimensionamento della trave in cls armato, quindi mantengo lo stesso interasse di 4 m e la luce di 4. In più devo assegnare un tipo di acciaio: S235. Con i dati assegnati, il file mi calcola automaticamente il M_max e fd, così da ottenere un Wx minimo.

Scelgo quindi dalla tabella dei profilati IPE la sezione con un Wx maggiore.

Sclego un IPE 360X170

TRAVE IN LEGNO

Carico strutturale (qs)

-tavolato, (0,03 m x 1 m x 1 m) /mq x 7 KN/mc = 0,21 KN/mq

-travetti, 2(0,1 m x 0,14 m x1 m) /mq 6 KN/mq = 0,168 KN/mq

Qs = 0,21 KN/mq + 0,168 KN/mq = 0,378 KN/mq

Carico portato (qp)

-pavimento, 0,3 KN/mq

-massetto, (0,03 m x 1 m x 1 m) /mq x 19 KN/mc = 0,57 KN/mq

-allettamento, (0,06 m x 1 m x 1 m) /mq x 14 Kn/mc = 0,84 KN/mq

Qp = 0,3 KN/mq + 0,57 KN/mq + 0,84 KN/mq = 1,71 KN/mq

Carico accidentale (qa)

Prendendo la tabella dalla normativa ho ipotizzato un uso residenziale quindi ho:

Qa = 2 KN/mq

Compilo il foglio Excel con i tre carichi così da calcolare il qu, che è la somma dei tre carichi x dei coefficienti di sicurezza x l’interasse.

In seguito aggiungo la luce del solaio, in modo da ottenere il M_max.

Inserisco i dati relativi al tipo di legno scelto per la trave da progettare in modo tale da ottenere la tensione di progetto

 imposto una base di 30 cm ottenendo una H_min pari a 27,05

Ingegnerizzo questa misura prendendo H = 35

La seconda esercitazione consiste nel dimensionamento di una trave inflessa considerando le tre principali tecnologie, ossia acciaio, legno e calcestruzzo.

Come prima cosa è necessario disegnare l’impalcato strutturale di un solaio (travi principali, secondarie e travetti) e individuare la trave principale con la maggiore area di influenza –a parità di area di influenza consideriamo la trave con la luce maggiore-.

In questo caso abbiamo una trave di luce 4,5m e un interasse di 3,5m, pertanto l’area di influenza è di 15,75m².

Per poter dimensionare una trave, dobbiamo tener conto di tre distinte tipologie di carico:

1. Il peso proprio (qs) rappresenta il peso della struttura portante;
2. I sovraccarichi permanenti (qp) sono tutti quelli che scaricano costantemente sul solaio (intonaco, controsoffitto, massetto di allettamento, pavimento, incidenza dei tramezzi, incidenza degli impianti);
3. Il sovraccarico accidentale (qa) è rappresentato dal sovraccarico d’uso, che varia in funzione della destinazione d’uso dell’edificio, più un sovraccarico del sottotetto per la manutenzione.

Di conseguenza la combinazione a stato limite ultimo è q_u = 1,3·q_s + 1,5·q_p + 1,5·q_a  in cui 1,3 e 1,5 sono coefficienti di sicurezza imposti dalla normativa per cautelarci da eventuali collassi.

SOLAIO IN ACCIAIO

1.Calcolo peso proprio strutturale (qs)

• Lamiera grecata = 0,12 kN/m²
• Cls alleggerito = (0,075mx12kN/m³ + 0,15mx12kN/m³)/2 = 1,35 kN/m²
• TOT = 1,47 kN/m²

2.Calcolo carico permanente (qp)

• Pavimentazione = 0,4kN/m²
• Massetto = 0,035mx21kN/m³ = 0,73kN/m²
• Isolante in fibra di legno = 0,04mx1,6 kN/m³ = 0,064kN/m²
• Incidenza impianti = 0,5kN/m²
• Incidenza tramezzi = 1kN/m²
• TOT = 2,69 kN/m²

3.Calcolo carico accidentale (qa)

• Uso residenziale = 2kN/m²

A questo punto è possibile inserire i dati ottenuti per il dimensionamento della trave all’interno del foglio Excel (compresi luce e interasse) in modo da ottenere la combinazione a stato limite ultimo q_u, il momento Mmax e il modulo di resistenza W_xmin.

Carico distribuito q_u

qu = (1,3 qs + 1,5 qp + 1,5 qa) x interasse

M max

Si tratta di una trave doppiamente appoggiata il cui momento massimo si trova alla mezzeria della luce e equivale a ql²/8, in cui “l” è la luce dell’elemento e “q” il carico qu distribuito.

W_x min

Utilizzando la formula di Navier σ_max = (M_max/I_x) y_max in cui I_x è il momento d’inerzia della sezione secondo l’asse x e y è la distanza massima delle fibre dall’asse baricentrico, si ricava W_min = M_max/f_d in cui fd è la resistenza di progetto dell’acciaio scelto.

Wmin < Wdesign

trave scelta :IPE 240

SOLAIO IN LEGNO

1.Calcolo peso proprio strutturale (qs)

• Travetti in legno = [(0,08mx0,12m)·6kN/m³ ]n_travetti = 0,11 kN/m²
• Tavolato in legno = 0,03mx6kN/m³= 0,18 kN/m²
• TOT = 0,29 kN/m²

2.Calcolo carico permanente (qp)

• Pavimentazione = 0,4kN/m²
• Massetto = 0,035mx21kN/m³ = 0,73kN/m²
• Isolante in fibra di legno = 0,04mx1,6 kN/m³ = 0,064kN/m²
• Incidenza impianti = 0,5kN/m²
• Incidenza tramezzi = 1kN/m²
• TOT = 2,69 kN/m²

3.Calcolo carico accidentale (qa)

• Uso residenziale = 2kN/m²

A questo punto è possibile inserire i dati ottenuti per il dimensionamento della trave all’interno del foglio Excel (compresi luce e interasse) in modo da ottenere la combinazione a stato limite ultimo q_u, il momento Mmax e la resistenza di progetto f_d.

Da questo valore, fissando una base si determina l’altezza minima che la sezione della trave deve avere.

SOLAIO IN LATEROCEMENTO

1.Calcolo peso proprio strutturale (qs)

• Pignatte = 0,12 kN/m²
• Travetti = [(0,14mx0,25m)·25kN/m³ ]n_travetti = 1,75 kN/m²
• Gettata in cls = 0,05m·25kN/m³= 1,25 kN/m²
• TOT = 3 kN/m²

2.Calcolo carico permanente (qp)

• Pavimentazione = 0,4kN/m²
• Massetto = 0,035mx21kN/m³ = 0,73kN/m²
• Isolante in fibra di legno = 0,04mx1,6 kN/m³ = 0,064kN/m²
• Incidenza impianti = 0,5kN/m²
• Incidenza tramezzi = 1kN/m²
• TOT = 2,69 kN/m²

3.Calcolo carico accidentale (qa)

• Uso residenziale = 2kN/m²

A questo punto è possibile inserire i dati ottenuti per il dimensionamento della trave all’interno del foglio Excel (compresi luce e interasse) in modo da ottenere la combinazione a stato limite ultimo q_u, il momento Mmax e la resistenza di progetto sia dell’acciaio che compone l’armatura sia del calcestruzzo.

Da questo valore, fissando una base si determina l’altezza minima che la sezione della trave deve avere fino al centro delle aree dell’armatura, a cui bisogna aggiungere un certo delta che rappresenta la distanza tra il centro delle aree dell’armatura e la “fibra” maggiormente tesa.

SOLAIO IN LEGNO (Impalcato di una casa unifamiliare)

CARICO ACCIDENTALE (valido per tutte e tre le tipologie di solaio)

dipende dalla tipologia edilizia, abitativa: qa=200kg/mp ----> 2 KN/mq

Prendo in esame la trave 4-7 perche è quella maggiormente sollecitata.

Interasse di 4,75m 

Area di influenza di 23,75mq

CARICO STRUTTURALE   (Trave + Travetti + Regolo)

qs= 0,7KN/mq

CARICO PERMANENTE (Pavimento + Malta di allettamento + Massetto + Tavolato + Controsoffitto)

-Pavimento: -Peso specifico: Yp= 400KN/mc

                    -Area: Ap= (25*3)*2= 150cmq =  0,015mq

                    -Carico strutturale: qpp= Ap * 1 * Yp=0,015*1*400=6Kg/m

-Malta di Allettamento: -Peso specifico: Ya= 1700Kg/mc

                                     -Area: Aa=2*50= 100cmq = 0,01mq

                                     -Carico strutturale: qpa = Aa*1*Ya = 0,01*1*1700 = qpa= 17Kg/m

-Massetto: -Peso specifico: Ym = 1400 Kg/mc

                  -Area: Am=5*50= 250 cmq = 0,025mq

                  -Carico strutturale: qpm = Am*1*Ym = 0,025*1*1400 = 35Kg/m

-Tavolato: -Peso specifico: Yt= 600Kg/mc

                 -Area: At=5*50= 250 cmq= 0,025mq

                 -Carico strutturale: qpt = At*1*Yt = 0,025*1*600 = 15 Kg/m

-Cpntrosoffitto: -Peso specifico: Yc = 2000Kg/mc

                         -Area: Ac=1,5*50 = 75 cmq = 0,0075mq

                         -Carico strutturale: qpc = Ac*1*Yc = 0,0075*1*2000 = 15 Kg/m

Carico permanente totale --> qp = qpp + qpa + qpm + qpt + qpc = 6+17+35+15+15 = 88Kg/m --> 0,88KN/m 

                                         -->qp = 1,76 KN/mq

SOLAIO IN ACCIAIO (Impalcato di una casa unifamiliare)

CARICO ACCIDENTALE (valido per tutte e tre le tipologie di solaio)

dipende dalla tipologia edilizia, abitativa: qa=200kg/mp ----> 2 KN/mq

Prendo in esame la trave 4-7 perche è quella maggiormente sollecitata.

Interasse di 4,75m 

Area di influenza di 23,75mq

CARICO STRUTTURALE (Travetto IPE + Lamiera grecata + Getto di CLS)

qs = 1,7 KN7Mq

CARICO PERMANENTE (Pavimento + Malta di allettamento + Isolante + Controsoffitto)

-Pavimento: -Peso specifico: Ya = 400 Kg/mc

                    -Area: Ap = (25*3)*2 = 150cmq = 0,015 mq

                    -Carico strutturale: qpp= Ap*1*Yp = 0,015*1*400 = 6Kg/m

-Malta di allettamento: -Peso specifico: Ya = 1700Kg/mc

                                    -Area: Aa =2*50 = 100cmq = 0,01mq

                                    -Carico strutturale: qpa = Aa*1*Ya = 0,01*1*1700= 17Kg/m

-Isolante: -Peso specifico: Yi=600Kg/mc

                -Area: Ai = 0,3*50 = 15 cmq = 0,0015mq

                -Carico strutturale: qpi = Ai*1*Yi = 0,0015*1*600 = 0,9Kg/m

-Cpntrosoffitto: -Peso specifico: Yc = 2000Kg/mc

                         -Area: Ac=1,5*50 = 75 cmq = 0,0075mq

                         -Carico strutturale: qpc = Ac*1*Yc = 0,0075*1*2000 = 15 Kg/m

Carico permanente totale ---> qp = qpp + qpa + qpi + qpc = 6+17+0,9+15 = 38,9 kG7m ---> 0,38 KN/m

                                         ---> qp = 0,778 KN/mq

Wx = 422,94 cmc   --->    scelgo quindi un IPE 300

SOLAIO IN LATERO-CEMENTO

CARICO ACCIDENTALE (valido per tutte e tre le tipologie di solaio)

dipende dalla tipologia edilizia, abitativa: qa=200kg/mp ----> 2 KN/mq

Prendo in esame la trave 4-7 perche è quella maggiormente sollecitata.

Interasse di 4,75m 

Area di influenza di 23,75mq

CARICO STRUTTURALE (Calcestruzzo + Pignatta)

-Calcestruzzo: -Peso specifico: Yc = 2500 kg/mc

                        -Area: Ac = (50*22)-(18*40) = 0,038mq

                        -Carico strutturale: qps = Ac*1*Yc = 0,038*1*2500 = 95Kg/m

-Pignatta: -Peso specifico laterizio: YL = 800Kg/mc

                -Area: AL = (20*18)*2 = 0,072 mq

                -Carico strutturale: qsL = AL*1*YL = 0,072mq*1*800 = 57,6 Kg/m

Carico strutturale totale: qs = qsc + qsL = 95+57,6 = 152,6 Kg/m ---> 1,526 KN/m 

                                       ----> qs=3,05 KN/mq

CARICO PERMANENTE (Pavimento + Malta di allettamento + Isolante + Massetto + Intonaco)

-Pavimento: -Peso specifico: Yp = 400 Kg/mc

                     -Area: Ap = (25*3)*2 = 150 Kg/cmq = 0,015 mq

                     -Carico struttirale: qpp = Ap*1*Yp = 0,015*1*400 = 6Kg/m

-Malta di allettamento: -Peso specifico: Ya = 1700 Kg/mc

                                    -Area: Aa=2*50 = 100cmq = 0,01mq

                                    -Carico strutturale: qpa = Aa*1*Ya = 0,01*1*1700 = 17 Kg/m

-Isolante: -Peso specifico: Yi = 600 Kg/mc

                -Area: Ai = 0,3*50=15cmq =0,0015 mq

                -Carico strutturale: qpi = Ai*1*Yi = 0,0015*1*600 = 0,9 Kg/m

-Massetto: -Peso specifico: Ym: 1400 Kg/mc

                  -Area: Am = 5*50 = 250 cmq = 0,025 mq

                 -Carico strutturale: qpm = Am*1*Ym = 0,025*1*1400 = 35 Kg/m

-Intonaco: -Peso specifico: Yin = 2000 Kg/mc

                 -Area: Ain=1,5*50 = 75 cmq = 0,0075 mq

                 -Carico strutturale: qpin = Ain*1*Yin = 0,0075*1*2000 = 15 Kg/m

Carico permanente totale: qp = qpp + qpa + qpi + qpm + qpin = 6+17+0,9+35+15 = 73,9 Kg/m __> 0,75 KN/m

                                          ----> qp = 1,478 KN/mq

In questa esercitazione ci troviamo davanti al problema di dimensionare la sezione di una trave a sbalzo in legno, calcestruzzo armato e acciao.

L’impalcato di riferimento si rifà a quello dell’esercitazione precedente modificato per realizzare l’aggetto: questo grazie l’arretramento della fila di pilastri di destra di 2,5 metri.

INTERASSE = 3,5 m

LUCE = 2,5 m

AREA INFLUENZA = 8,75 m²

Passo 1: Trovata l’area d’influenza maggiore tra le travi a sbalzo il procedimento di dimesionamento iniziale è lo stesso utilizzato nell’esercitazione precedente (link) con due modifiche sostanziali:

• Il momento massimo M_MAX sarà quello di una mensola quindi uguale a q_ul²/2 ;
• Il carico accidentale q_a sarà equivalente a 4 kN/m² , coefficiente dato dalla Normativa per carici accidentali su balconi (categoria C2).

Passo 2: Dopo aver dimensionato la sezione, dobbiamo effettuare la verifica a deformabilità controllando che l’abbassamento massimo della trave in rapporto con la sua luce deve essere maggiore di 250 (valore dato da Normativa):

                                            l/ v_max > 250

Dove :

                                            v_max = ql⁴/8EI

Per trovare v_max è necessario utilizzare il metodo della linea elastica, vediamo i passaggi:

• Il momento flettente nella generica sezione x è uguale a M = -qx²/2
• Ci troviamo la curvatura χ = (qx²/2) (1/EI)
• Integriamo χ e troviamo la rotazione ϕ = (qx³/6) (1/EI) + C₁
• Integriamo nuovamente trovando lo spostamento v = (qx⁴/24) (1/EI) + C₁x + C₂
• Osserviamo che in corrispondenza dell’incastro B (x=l) devono essere nulli tanto l’abbassamento quanto la rotazione.
• Quindi per x=l si ottiene  C₁ = -ql³/6  e C₂ = ql⁴/8
• Infine sostituendo le due costanti d’integrazione a v ci troviamo l’abbassamento massimo v_max = ql⁴/8EI

Questo procedimento vale per tutte e tre le tecnologie e si effettua allo SLE quindi i carichi sulla struttra verrano ricombinati con la combinazione di carico agli SLE data da normativa.

Andiamo ora a dimensionare le tre tecnologie strutturali ( i solai sono gli stessi dell’esercitazione precedente)

CALCESTRUZZO ARMATO

Fatto il passo 1 la sezione della mia trave in calcestruzzo armato equivale a 30x50 cm.

Come nell’esercitzione precedente riverifico che la sezione sia verificata aggiungendo nel q_u il peso della trave.

Applico la combinazione di carico agli SLE ed inserisco il modulo di elasticità del cls armato in modo da trovarmi il momento d’inerzia I_x .

Ora abbiamo tutti gli elementi per calcolarci il v_max

LEGNO

Fatto il passo 1 la sezione della mia trave in legno equivale a 25x45 cm.

Non c’è bisogno di verificare il peso proprio della trave poichè il legno ha peso specifico basso.

Applico la combinazione di carico agli SLE ed inserisco il modulo di elasticità del cls armato in modo da trovarmi il momento d’inerzia I_x .

Ora abbiamo tutti gli elementi per calcolarci il v_max

ACCIAIO

Fatto il passo 1 il profilato preso è di un IPE 300.

Successivament controllo che la sezione sia verificata aggiungendo nel q_u il peso della trave.

Applico la combinazione di carico agli SLE ed inserisco il modulo di elasticità del cls armato in modo da trovarmi il momento d’inerzia I_x .

Ora abbiamo tutti gli elementi per calcolarci il v_max