Blog

Prendendo in considerazione i dati calcolati nella precedente esercitazione (carichi deI solai) , vado a ricavarmi l'altezza minima della trave per quanto riguarda il cemento armato ed il legno e la resistenza a flessione minima per l'acciaio. Dovendo progettare una trave a sbalzo l'unica differenza di calcolo che si può riscontrare rispetto alla precedente esercitazione è  nella formula del momento massimo ,infatti la formula non saraà più  q_ul²/8  poichè il sistema equivale a quello di una mensola per cui in corrispondenza della sezione ad incastro avremo:

M= q_ul²/2 

 

MENSOLA IN CALCESTRUZZO

Riporto i dati che mi servono per il calcolo dei carichi q_s (carichi strutturali) e q_p (carichi portati):

MATERIALE                                                                                                        SPESSORE[m]                                                                                                      

- pavimento in cotto                                                   24 Kg/mq                                        0,02
- malta di sottofondo                                                  18 KN/mc                                        0,02
- strato di allettamento in cls                                       24 KN/mc                                        0,03
- isolante in lana di vetro                                            20 Kg/mc                                         0,08
- cls alleggerito                                                         18 KN/mc                                        0,04
- pignatta                                                                 9,1 Kg        
- intonaco in gesso                                                     13 KN/mc                                        0,01

q_s_carico strutturale (soletta collaborante, travetti, pignatta)

- soletta collaborante:              (0,04m x 1m x 1m)/mq x 24KN/mc = 0,96 KN/mq
- travetti:                             2(0,10m x 0,16m x 1m)/mq x 24KN/mc = 0,768 KN/mq
- pignatta:                            8 x 9,1 Kg/mq = 72,8 Kg/mq = 0,728 KN/mq

q_s = (0,96 + 0,768 + 0,728) KN/mq = 2,45 KN/mq

q_p_carico portato (pavimento, malta, allettamento, isolante, massetto delle pendenze, intonaco)

- pavimento in cotto:                        24Kg/mq = 0,24KN/mq
- malta di sottofondo:                       (0,02m x 1m x 1m)/mq x 18KN/mc = 0,36KN/mq
- strato di allettamento in cls             (0,03m x 1m x 1m)/mq x 24KN/mc= 0,72KN/mq
- isolante in lana di vetro                  (0,08m x 1m x 1m)/mq x 0,2KN/mc = 0,016KN/mq
- massetto delle pendenze                 (0,04m x 1m x 1m)/mq x 18KN/mc = 0,72KN/mq
- intonaco                                       (0,01m x 1m x 1m)/mq x 13KN/mc = 0,13KN/mq
- impianti + tramezzi                        1,5KN/mq

q_p = (0,24 + 0,36 + 0,72 + 0,016 + 0,72 + 0,13 + 1,5)KN/mq = 3,68 KN/mq

q_a_carico accidentale

Prendendo la tabella della normativa ho ipotizzato un uso residenziale e quindi:

q_a = 2KN/mq

 

MENSOLA IN ACCIAIO

Riporto i dati che mi servono per il calcolo dei carichi q_s (carichi strutturali) e q_p (carichi portati):

MATERIALE                                                                                                      SPESSORE[m]                                                                                                                  

- pavimento in cotto                                                   24 Kg/mq                                      0,02
- malta di sottofondo                                                  18 KN/mc                                      0,02
- massetto in cls alleggerito                                         18 KN/mc                                      0,03
- isolante in lana di roccia                                            90 Kg/mc                                      0,04
- lamiera grecata                                                        9 Kg/mq                                         
- soletta + metà trapezi                                               18 KN/mc                                     0,0925
  rimepiti in cls alleggerito                                                                              
- cartongesso                                                             20 Kg/mq                                     0,015
- IPE 160                                                                   77,1 KN/mc                          0,00201 m²  
                                                                                                             (Area della sezione)
                                                                                                                           

Per semplificarmi i calcoli, quando andrò a calcolare il peso del riempimento in cls della lamiera grecata,
immagino di dividere in due la parte dei trapezi. Così facendo avrò la parte piena che perdo pari a quella vuota,
così posso sommare direttamente lo strato della soletta (6,5 cm) con metà trapezio (5,5cm/2), evitando il 
calcolo del singolo trapezio.

q_s_carico strutturale (lamiera grecata, getto in cls, IPE 160)

- lamiera grecata:                                       9Kg/mq = 0,09 KN/mq 
- getto in cls alleggerito                               (0,0925m x 1m x 1m)/mq x 18KN/mc = 1,665KN/mq
- IPE 160                                                   2(0,00201mq x 1m)/mq x 77,1KN/mc = 0,31KN/mq

q_s = (0,09 + 1,665 + 0,31)KN/mq = 2,065 KN/mq

q_p_carico portato (pavimento, malta di allettamento, massetto in cls alleggerito, isolante, cartongesso)

-pavimento in cotto:                                 24Kg/mq = 0,24 KN/mq
- sottofondo in malta:                               (0,02m x 1m x 1m)/mq x 18KN/mc = 0,36KN/mq
- massetto in cls alleggerito                       (0,03m x 1m x 1m)/mq x 18KN/mc = 0,54KN/mq
- isolante lana di roccia                             (0,04m x 1m x 1m)/mq x 0,9KN/mc = 0,036KN/mq
- cartongesso                                          20Kg/mq = 0,2KN/mq
- impianti + tramezzi                                1,5KN/mq

q_p = (0,24 + 0,36 + 0,54 + 0,036 + 0,2 + 1,5)KN/mq = 2,876KN/mq 

q_a_carico accidentale

Prendendo la tabella della normativa ho ipotizzato la costruzione di uffici aperti al pubblico:

q_a = 3KN/mq

 

MENSOLA  IN LEGNO

 

Riporto i dati che mi servono per il calcolo dei carichi qs (carichi strutturali) e qp (carichi portati):

MATERIALE                                                                                                        SPESSORE[m]                                                                                                                   

- pavimento in cotto                                                   24 Kg/mq                                         0,02
- malta di sottofondo                                                  18 KN/mc                                         0,02
- pannello isolante + tubi radianti                                 14,5 KN/mc                                      0,04
- isolante in fibra di legno                                           0,18 KN/mc                                       0,06
- caldana in cls alleggerito                                           18 KN/mc                                         0,03
- tavolato in legno di Rovere                                        7,0 KN/mc                                        0,03
- travetti in legno                                                       6 KN/mc                                 0,12 x 0,16

q_s_carico strutturale (tavolato, travetti)

- tavolato:                 (0,03m x 1m x 1m)/mq x 7KN/mc = 0,21KN/mq
- travetti                   2(0,12m x 0,16m x 1m)/mq x 6KN/mc = 0,23KN/mq

q_s = (0,21 + 0,23)KN/mq = 0,44KN/mq

q_p_carico portato (pavimento, malta, pannello radiante, isolante, caldana)

-pavimento in cotto:                                 24Kg/mq = 0,24 KN/mq
- sottofondo in malta:                               (0,02m x 1m x 1m)/mq x 18KN/mc = 0,36KN/mq
- isolante + tubi radianti                           (0,04m x 1m x 1m)/mq x 14,5KN/mc = 0,58KN/mq
- isolante fibra di legno                             (0,06m x 1m x 1m)/mq x 0,18KN/mc = 0,0108 KN/mq
- caldana in cls alleggerito                         (0,03m x 1m x 1m)/mq x 18KN/mc = 0,54 KN/mq
- impianti + tramezzi                                1,5KN/mq

q_p = (0,24 + 0,36 + 0,58 + 0,0108 + 0,54 + 1,5)KN/mq = 3,328KN/mq 

q_a_carico accidentale

Prendendo la tabella della normativa ho ipotizzato un uso residenziale e quindi:

q_a = 2KN/mq

La q_m², ossia la combinazione di carico per lo stato limite ultimo, non nasce dalla somma dei tre carichi (q_a,q_p,q_s) ma dalla moltiplicazione di questi con dei coefficienti moltiplicativi utilizzati nella combinazione:

q_m²=γ_g1*q_s+ γ_g2*q_p + γ_g3*q_a

q_m²=1,3*q_s+ 1,5*q_p +1,5*q_a

Trovato quindi il carico che si riferisce ad 1 m² di solaio bisognerà trovare il valore del caricoq_solaio che nasce dalla moltiplicazione dell' Area di influenza della trave per la combinazione di carico

q_solaio = A*q_m²  dove A = interasse* luce della trave

CEMENTO

 

ACCIAIO

Nel nostro caso abbiamo un W_xmin= 1004,92 cm³, per questo motivo andiamo a scegliere un profilato IPE400 con un W_x= 1156 cm³

 

LEGNO

 

DEFORMABILITA'

Dopo aver progettato la sezione della mia trave in tutte le tecnologie, per questo sistema statico si considera  un altro fattore: la deformabilità. La verifica a deformabilità  si basa sul rapporto della luce della mia trave (sbalzo) e l'abbassamento massimo, che deve essere >250. Essa non viene effettuata allo SLU (stato limite ultimo -collasso), ma allo SLE (stato limite di esercizio-funzionalità ed efficienza), poichè la verifica mira a controllare che non ci siano spostamenti e deformazioni che possano diminuire l' efficienza e l' aspetto della costruzione.

Per questo motivo i carichi sulla trave a sbalzo vengono riconsiderati utilizzando una combinazione utilizzata per gli stati limiti di eserzio reversbili:

q_e= (G1 + G2 + ψ_11*Q₁) _* i dove

G1 rappresenta il valore caratteristico del peso proprio di tutti gli elementi strutturali; G2 è il valore caratteristico del peso proprio di tutti gli elementi non strutturali (q_p); ψ₁₁ rappresenta il coefficiente che definisce il valore frequente dell’azione variabile Q1 che invece è il valore caratteristico dell’azione variabile (q_a);mentre i equivale al nostro interasse.

Nel caso della mensola in legno, che è un materiale leggero, il peso proprio della trave viene trascurato mentre al contrario, nella trave in acciaio e in cemento, questo ragionamento non viene preso in esame dato che il peso di entrambi i materiali ha un contributo significativo.

Prendendo in esame la mensola in acciaio abbiamo detto precedentemente che abbiamo trovato un                       W_xmin = 1004,92 cm³, per ingegnerizzare la sezione si sceglierà  un  I_x che avrà come Modulo di Resistenza  un valore maggiore a quello minimo trovato, infatti  avendo scelto una trave IPE400 il W_x= 1156 cm³ > W_xmin = 1004,92 cm³.

Avendo scelto il profilo possiamo adesso aggiungere il peso espresso in Kn/m a seconda del tipo di profilato scelto.

 

 

 

Per quanto riguarda il cemento il peso proprio della struttura era già stato calcolato poichè era necessario verificare allo SLU che la sezione scelta potesse sopportare i carichi anche dopo aver aggiunto il peso proprio, in questo modo possiamo arrivare a calcolare il carico totale sulla trave q_e .

q_e cemento= 41,65 kN/m

 

q_e acciaio=30,36 kN/m

 

q_e legno=24 kN/m

 

Per poterci calcolare lo spostamento abbiamo bisogno di altri due parametri: il modulo elastico E e  il momento di Inerzia I_x.

E_cemento = 2100 N/mm²

E_acciaio = 210000 N/mm²

Elegno= 8000 N/mm²

I_x cemento = 720000 cm⁴ 

I_x acciaio = 23130 cm⁴ ( che precedenemente avevamo calcolato una volta scelta la sezione della trave)

I_x legno = 554583 cm⁴ (che nasce come prodotto tra b*H³/12 ossia nel nostro caso I_{x legno}= 30*55³ /12 )

In questo modo possiamo andarci a calcolare l' abbassamento di una trave a sbalzo sottoposta ad un carico uniformemente distribuito:

 v_max= - (q_e*l⁴)/8_*E_*I_x

_CEMENTO

ACCIAIO    

                       

LEGNO

 

Come ultimo procedimento dobbiamo verificare che il rapporto tra la luce della trave e il suo abbassamento massimo sia > 250 che varia da normativa a seconda del tipo di elemento strutturale, nel nostro caso possiamo parlare di solai generici quindi : 

l/ v_max > 250

             

Nel nostro caso 

l/ v_max,cemento = 1075,63

l/ v_max,acciaio = 474,045

l/ v_max,legno = 551,18 

Possiamo notare che la verifiche effettuate sono andate tutte a buon fine.

CEMENTO

 

ACCIAIO

LEGNO

L'obiettivo dell'esercitazione è analizzare la deformabilità di una trave a sbalzo maggiormente sollecitata attraverso l'utilizzo di tre tecnologie costruttive differenti: ACCIAO - LEGNO - CLS.

Si prende in esame una pianta destinata ad uso residenziale e tramite l'orditura del solaio si trova:

• Area di Influenza    = 20 mq
• Luce                        = 4 m
• Interasse                 = 5 m

Per prima cosa bisogna trovare le stesse informazioni come nell'esercitazione 2, ovvero, calcolare il dimensionamento della trave. In questo caso però il momento flettente massimo, M_max,  sarà calcolato non più con l'equazione di una trave doppiamente appoggiata ma con l'equazione di una mensola ad incastro:

                                                      M_max = (q_u l²)/2                            

                             

Dopo aver dimensionato la sezione si deve effettuare la verifica a deformabilità controllando l'abbasamento massimo della trave in rapporto alla sua luce. Questo si effettua allo Stato Limite di Esercizio SLE, stato subito dopo il quale la struttura non si rompe, ma a causa di spostamenti e deformazioni cambia nella sua conformazione limitando la possibilità d’utilizzo dell’edificio. 

Si calcolano perciò nuovamente i carichi incidenti sulla struttura moltiplicando il coefficiente di combinazione ψ al q_a :

                                                    q_e = (q_{s +} q_{p +} q_a x ψ) x i 

Nel caso dell'acciaio e del cemento armato si tiene conto del peso propro della trave, dunque si moltiplica al q_e, mentre nel caso del legno no pechè è un materiale leggero e quindi viene trascurato il valore del peso proprio.

Si trova il modulo elastico E ed il momento di Inerzia I_x per poter calcolare successivamente l'abbassamento massimo ν_max :

                                                     ν_max = (q_e l⁴)/8EI_x   

                         

Si può così verificare se il rapporto tra la luce della trave e il suo abbassamento massimo sia maggiore a 250, come imposto dalla normativa. 

Si riprende la stessa tecnologia del solaio studiati nell'esercitazione 2:

SBALZO TRAVE ACCIAIO

q_P =  0,19 + 0,6 + 0,03 + 1,0 + 0,5 =  2,32 KN/m²

• pavimentazione in gres porcellanato: 0,19 KN/m²
• massetto di tipo tradizionale: 0,03 m x 20 KN/m³ = 0,6 KN/m²
• isolamento acustico ACUSTIC SYSTEM 7: 0,03 KN/m²
• tramezzi: 1,0 KN/m²
• impianti: 0,5 KN/m²

q_s = 2,44  + 0,188 = 2,628 KN/m²

• lamiera grecata mod. E/S 4000 e getto di calcestruzzo h 12 cm :  2,44 KN/m²
• travetto IPE 180 :  0,188 KN/m > 0,188 (KN/m)  / 1 (m_interasse) = 0,188 KN/m²

^​q_a =  2 KN/m²   ambienti ad uso residenziale

Calcolo il q_u e trovo M_{max .} 

Scelgo la classe di resistenza dell'acciaio f_yk = 275 MPa e trovo  f_yd e W_xmin .

Il valore W_xmin è 1511,45 cm³, dunque trovo sulla tabella dei profilati IPE il valore successivamente maggiore a quest'ultimo per definire il W_x di design, che è uguale a 1930,0 cm³ IPE 500.

Si aggiunge il peso della trave al q_s:

q_s = 2,44  + 0,188 + 0,181 = 2,8 KN/m²

• lamiera grecata mod. E/S 4000 e getto di calcestruzzo h 12 cm :  2,44 KN/m²
• travetto IPE 180 :  0,188 KN/m > 0,188 (KN/m)  / 1 (m_interasse) = 0,188 KN/m²
• trave IPE 300 :  0,907 KN/m > 0,907 (KN/m)  / 5 (m_interasse) = 0,181 KN/m²

​Calcolo ora il q_e  e nonostante il carico sia stato modificato, il rapporto tra la luce di libera inflessione e l'abbassamento massimo è maggiore di 250.

l/νmax=412,846 > 250  

            

Il dimensionamento risulta corretto.

 

SBALZO TRAVE LEGNO

q_P =  0,216 + 0,6 + 0,03 + 1,0 + 0,5 + 0,9 =  3,306 KN/m²

• pavimentazione in parquet di rovere:  0,03 m x 7,2 KN/m³  = 0,216 KN/m²
• massetto di tipo tradizionale: 0,03 m x 20 KN/m³ = 0,6 KN/m²
• isolamento acustico ACUSTIC SYSTEM 7: 0,03 KN/m²
• caldana: 0,04 m x 24 KN/m³ = 0,96 KN/m²
• tramezzi: 1,0 KN/m²
• impianti: 0,5 KN/m²

^​q_s =  0,21 + 0,036 =  0,246  KN/m²

• assito:  0,21 KN/m²
• travetti :  1m x 0,20m x 0,30m x 0,6 KN/m³ = 0,036 KN/m²

 q_a =  2 KN/m²   ambienti ad uso residenziale

 

Calcolo il q_u e trovo M_{max .} 

Scelgo il legno lammellare GL24h con f_mk = 24 con k_mod= 0,60 e γ_m= 1,45.

Posso calcolare la tensione di progetto f_d = 9,93

Imposto una base di 40 cm trovando così un h_min = 70,72 cm e la ingegnerizzo portandola a un H = 75 cm. Ottengo una trave 40x70cm.

In questo caso, come già detto, il legno è un materiale leggero e quindi il peso proprio della trave viene trascurato.

Calcolo il q_e = 23 KN/m e il rapporto tra la luce l e l'abbassamento risulta  > 250.

l/vmax= 617,86 >250.

Il dimensionamento risulta corretto.

 

SBALZO TRAVE C.A.

q_P =  0,19 + 0,6 + 0,03 + 0,13 + 1,0 + 0,5 =  2,45 KN/m²

• pavimentazione in gres porcellanato: 0,19 KN/m²
• massetto di tipo tradizionale: 0,03 m x 20 KN/m³ = 0,6 KN/m²
• isolamento acustico ACUSTIC SYSTEM 7: 0,03 KN/m²
• intonaco: 0,13 KN/m²
• tramezzi: 1,0 KN/m²
• impianti: 0,5 KN/m²

q_s = 3,19  +  0,053 = 3,243 KN/m²

• pignatta 20x40x25 + caldana 5 cm :  3,19 KN/m²
• rete elettrosaldata (maglia 15cmx15cm  ø8): 5,3 Kg/m² = 0,053 KN/m²

^​q_a =  2 KN/m²   ambienti ad uso residenziale

Calcolo il q_u e trovo M_{max .} 

Per l'acciaio scelgo la classe B450C che ha una resistenza di snervamento f_yk = 450 MPa e trovo: f_yd = 391,30 N/mm²

Per trovare invece la tensione di progetto del calcestruzzo scelgo come classe di resistenza f_ck (C 40/50) e trovo: f_cd = 17 N/mm²

Si trova  h_u, impostando una base di 45 cm, si aggiunge il valore δ per trovare H_min =62,65 cm. 

Questo valore si ingegnerizza portandolo alla decina superiore dunque : H = 70 cm.

Calcolo il q_e = 41,34 KN/m e il rapporto tra la luce l e l'abbassamento risulta  > 250.

l/vmax= 816,74 >250.

Il dimensionamento risulta corretto.

 

 

In questa esercirazione andiamo a dimensionare la trave appoggiata più sollecitata di un solaio, dimensionandola a flessione dunque e comparando diversi materiali: acciaio, legno e laterocemento.

Il solaio analizzato è il seguente e mette in evidenza la trave più sollecitata con la sua area d'influenza, ovvero di quale parte del solaio questa si fa carico.

 

 

 

 

 

 

 

 

 

 

 

 

 

ANALISI DEI CARICHI PER SOLAIO IN ACCIAIO 

 

 

 

 

Elementi del Solaio

Lamiera Grecata – spessore: 0.9 mm; altezza: 7 cm; Peso: 0,11 KN/m²

Getto di cls – altezza: 7 cm nella lamiera + 4 cm esterni; Peso Specifico: 25 KN/m³

Isolante – altezza 3 cm; Peso Specifico: 1,8 KN/m³

Massetto – altezza: 5 cm; Peso Specifico: 19 KN/m³

Pavimento – altezza: 3 cm; Peso Specifico: 20 KN/m³

 

Calcolo Carichi Strutturali

Lamiera Grecata: 0,11 KN/m²

Getto di cls: (25 KN/m³ x 0,04 m) + (25 KN/m³ x 0,07m) / 2 = 1 KN/m² + 0,875 KN/m² = 1,875 KN/m²

q_s= 0,11 KN/m² + 1,875 KN/m² = 1,985 KN/m²

 

Calcolo Carichi Permanenti

Isolante: 1,8 KN/m³ x 0,03m = 0,054 KN/m²

Massetto: 19 KN/m³ x 0,05 m = 0,95 KN/m²

Pavimento: 20 KN/m³ x 0,03 m = 0,6 KN/m²

Tramezzi: 1 KN/m²

Impianti: 0,5 KN/m²

q_p= 0,054 KN/m² + 0,95 KN/m² + 0,6 KN/m² + 1 KN/m² + 0,5 KN/m² = 3,104 KN/m²

 

Calcolo Carichi Accidentali

I carichi accidentali sono dati dalla normativa: essendo ad uso residenziale abbiamo che

q_a = 2 KN/m² 

 

DIMENSIONAMENTO A FLESSIONE

Una volta trovati tutti i carichi inserisco nella tabella excel del dimensionamento a flessione (nella sezione acciaio) i valori dei carichi ricavati, l'interasse, la luce della trave e scelgo una classe di acciaio (S275), in modo che moltiplicando i carichi per i loro coefficenti di sicurezza, moltiplicandoli per l'interasse e sommandoli, ottengo il mio carico ripartito sulla trave q_u.

So che il Momento massimo di una trave appoggiata sottoposta a un carico ripartito equivale a qL²/8; sapendo tutti i valori lo calcolo e grazie a questo mi trovo il W_{x min} (=M_max/f_yd).

 

 

Grazie a questo valore trovo un profilato industralizzato adeguato, ovvero con un W_x > W_{x min}: una IPE300

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ANALISI DEI CARICHI PER SOLAIO IN LATEROCEMENTO

 

 

 

 

 

Elementi del Solaio

Calcestruzzo armato – altezza: 5 cm + 25x10 cm dei travetti; Peso Specifico: 25 KN/m³

Pignatte – 12x50x25 cm; Peso: 1,05 KN/m² con travetti di interasse 60 cm

Isolante – altezza 3 cm; Peso Specifico: 1,8 KN/m³

Massetto – 5 cm; Peso Specifico: 19 KN/m³

Pavimento – 3 cm; Peso Specifico: 20 KN/m³

 

Calcolo Carichi Strutturali

Cls armato: 25 KN/m³ x 0,05m + [(0,025 m³ x 2) x 25 KN/m³] / m² = 1,25 KN/m² + 1,25 KN/m² = 2,5 KN/m²

Pignatte: 1,05 KN/m²

q_s= 2,5 KN/m² + 1,05 KN/m² = 3,55 KN/m²

 

Calcolo Carichi Permanenti

Isolante: 1,8 KN/m³ x 0,03m = 0,054 KN/m²

Massetto: 19 KN/m³ x 0,05 m = 0,95 KN/m²

Pavimento: 20 KN/m³ x 0,03 m = 0,6 KN/m²

Tramezzi: 1 KN/m²

Impianti: 0,5 KN/m²

q_p= 0,054 KN/m² + 0,95 KN/m² + 0,6 KN/m² + 1 KN/m² + 0,5 KN/m² = 3,104 KN/m²

 

Calcolo Carichi Accidentali

I carichi accidentali sono dati dalla normativa: essendo ad uso residenziale abbiamo che

q_a = 2 KN/m² 

 

DIMENSIONAMENTO A FLESSIONE

Trovo q_u nuovamente grazie ai carichi, i coefficenti e l'interasse e di conseguenza il Momento massimo. Inserisco le tensioni caratteristiche f_k di cls e acciaio (C60 e S450) e trovo le tensioni caratteristiche di progetto f_cd e f_yd grazie ai coefficenti.

A questo punto scelgo una dimensione per la base della mia trave (25 cm) e per il mio copriferro (5 cm) e grazie alla tabella excel ottengo un'altezza minima di 34,14 cm, dunque inizialmente ho scelto una trave 25x35 cm, in seguito però analizzando il carico con aggiunta del peso proprio, la trave non era verificata e l'altezza minima era di 35,4 cm, dunque ho scelto una trave 25x40 cm, in questo modo la sezione risulta verificata.

 

 

 

ANALISI DEI CARICHI PER SOLAIO IN LEGNO

 

 

 

 

 

Elementi del Solaio

Travetti – altezza: 10x20cm con 50cm di interasse; Peso Specifico: 4 KN/m³ (abete rosso)

Tavolato – altezza: 3 cm; Peso Specifico: 4 KN/m³ (abete rosso)

Isolante – altezza 3 cm; Peso Specifico: 1,8 KN/m³

Massetto – 5 cm; Peso Specifico: 19 KN/m³

Pavimento – 3 cm; Peso Specifico: 20 KN/m³

 

Calcolo Carichi Strutturali

Travetti: [(0,02 m³ x 2) x 4 KN/m³] / m² = 0,16 KN/m²

Tavolato: 4 KN/m³ x 0,03 m = 0,12 KN/m²

q_s= 0,16 KN/m² + 0,12 KN/m² = 0,28 KN/m²

 

Calcolo Carichi Permanenti

Isolante: 1,8 KN/m³ x 0,03m = 0,054 KN/m²

Massetto: 19 KN/m³ x 0,05 m = 0,95 KN/m²

Pavimento: 20 KN/m³ x 0,03 m = 0,6 KN/m²

Tramezzi: 1 KN/m²

Impianti: 0,5 KN/m²

q_p= 0,054 KN/m² + 0,95 KN/m² + 0,6 KN/m² + 1 KN/m² + 0,5 KN/m² = 3,104 KN/m²

 

Calcolo Carichi Accidentali

I carichi accidentali sono dati dalla normativa: essendo ad uso residenziale abbiamo che

q_a = 2 KN/m² 

 

DIMENSIONAMENTO A FLESSIONE

Nuovamente, trovati i diversi carichi trovo il carico distribuito q_u e calcolo il Momento massimo. A questo punto inserisco la tensione caratteristica del materiale da me scelto (Abete rosso) f_mk = 24 MPa, che moltiplicato per il fattore di umidità k_mod e diviso per il coefficente di sicurezza dà la tensione caratteristica di progetto  f_md.

Fatto questo scelgo un valore per la mia base, scegliendo tra i valori industrializzati (24 cm), trovo un'altezza minima pari a 45,21 cm, dunque scelgo un profilato 24x48 cm (sempre controllando tra i valori industrializzati).

 

 

Questa terza esercitazione prevede il dimensionamento della sezione di una trave a sbalzo nei tre materiali: legno, acciaio e calcestruzzo armato. I solai che si andranno ad utilizzare sono già stati indicati nella seconda esercitazione, in cui è stato eseguito il dimensionato della trave maggiormente sollecitata.

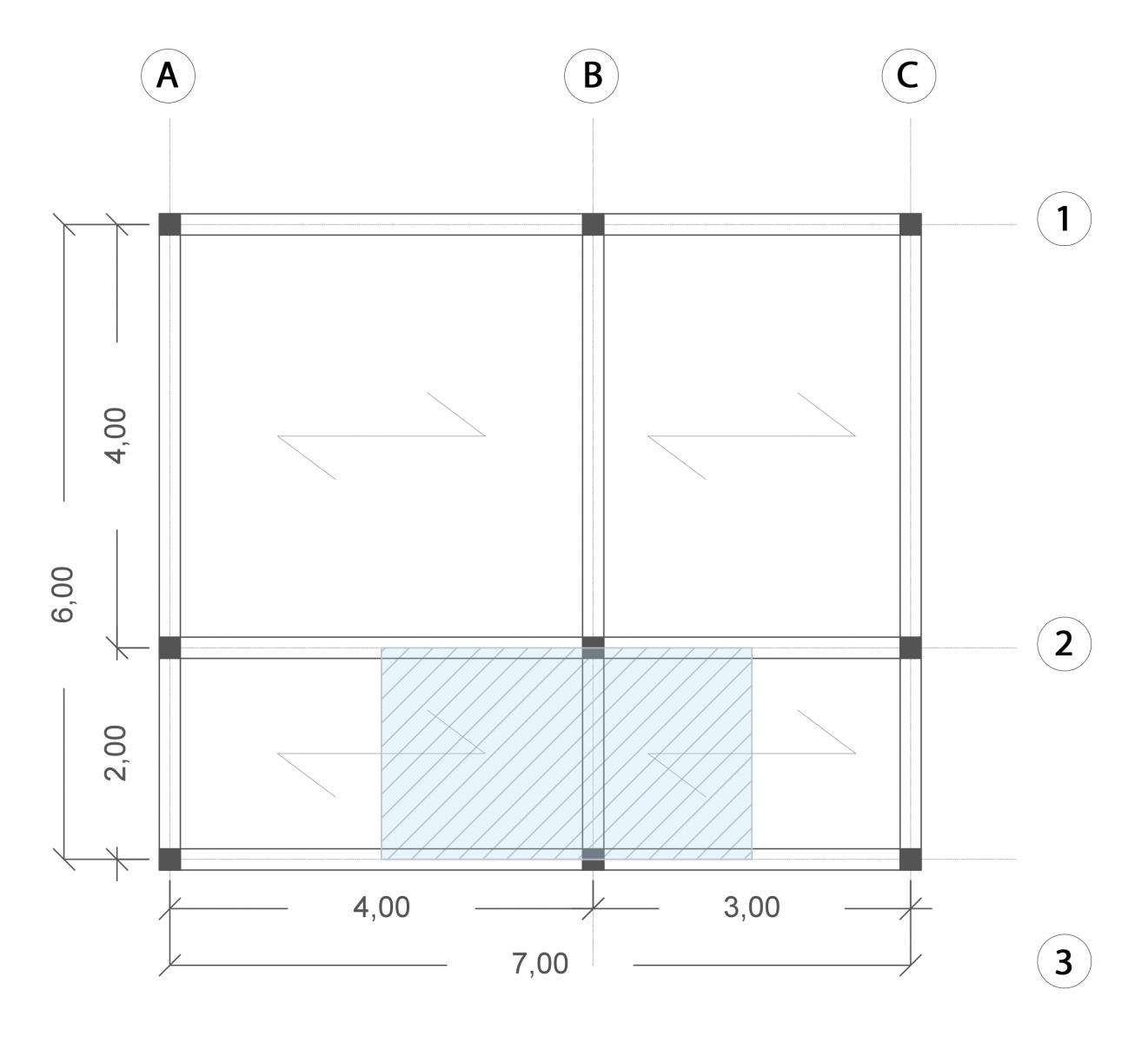
La carpenteria presenta uno sbalzo di 2 x 7 m e la trave maggiormente sollecitata è quella compresa tra i pilastri B2 e B3:  

l (luce) = 2 m;              

 i (interasse) = 2 m + 1,5 m = 3,5 m;                      

A ( area d’influenza) = 2 m x 3,5 m = 7 mq 

In questo caso il modello statico da considerare è quello di una mensola incastrata ad un’estremità.

           

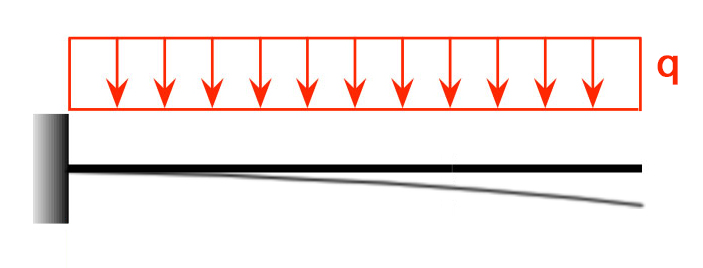
Il valore del momento massimo in corrispondenza della sezione d’incastro varrà -->  Mmax = qu x l^2/2

Inoltre, dopo aver eseguito il dimensionamento, è necessario effettuare la verifica a deformabilità per controllare che l’abbassamento massimo della trave sia inferiore a 1/250 della luce. Questa si effettua nelle condizioni dello stato limite d’esercizio (SLE), per evitare la perdita di funzionalità della struttura.

Per questa ragione i carichi che gravano sulla trave vengono calcolati secondo la combinazione frequente, impiegata per gli stati limite d’esercizio reversibili:

qe = (G1 + G2 + psi 11 x Q1) xi

I carichi strutturali, permanenti ed accidentali sono stati ripresi dalla precedente esercitazione.

 

ACCIAIO

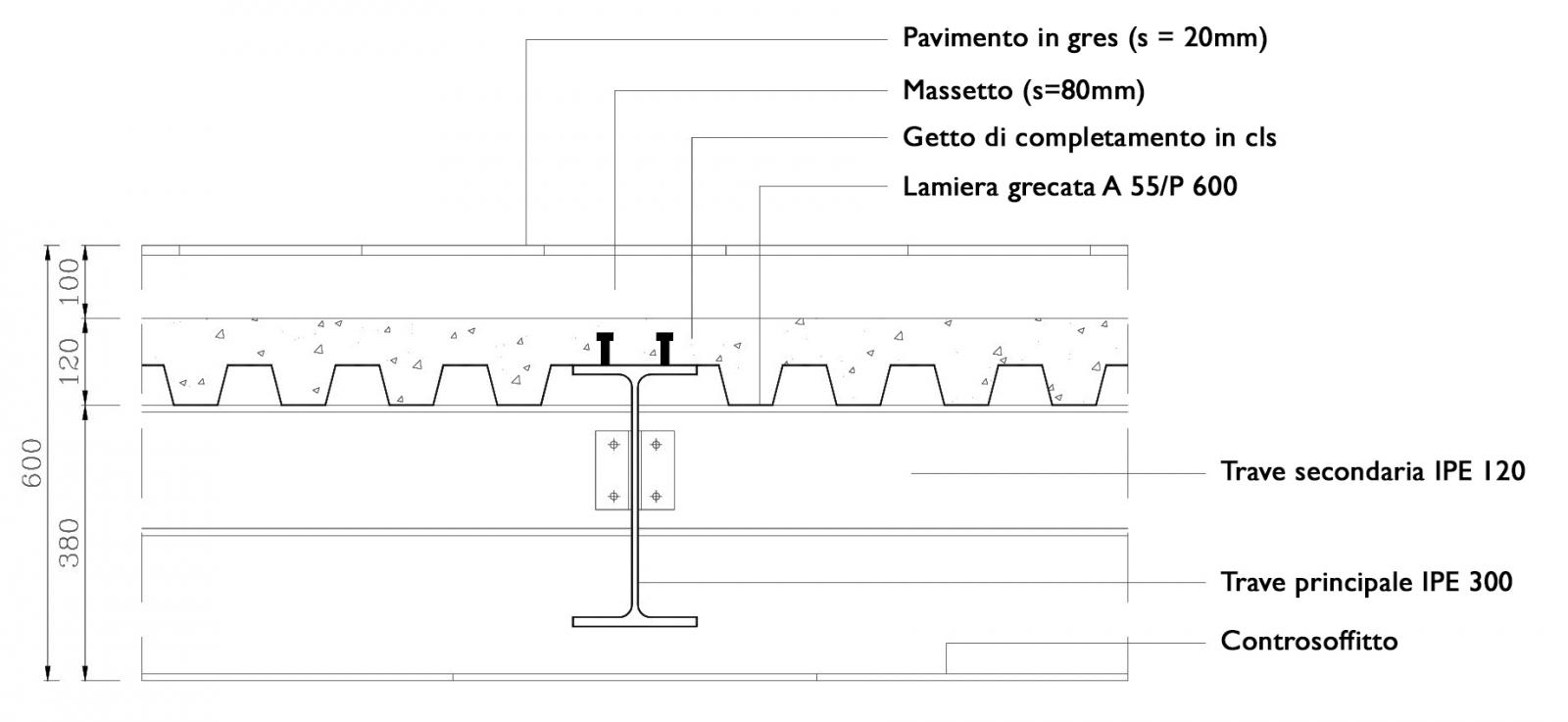
CARICHI STRUTTURALI

• Lamiera grecata (s = 0,8 mm) --> p.p = 10,47 kg/mq = 0,1047 KN/mq = 0,1 KN/mq                    
• Getto di cls  -->  γ = 25,00 KN/mc

                                      Smedio = 65 + 55 / 2 = 92,5 mm = 0,0925 m

                                      p.p. =  25 x 0,0925 = 2,32 KN/mq

TOTALE CARICHI STRUTTURALI = 2,42 KN/mq

 

CARICHI PERMANENTI

• Pavimento in gres (s = 20 mm)  --> p.p. =0,40 KN/mq
• Massetto in malta di cemento -->  γ = 25,00 KN/mc

                                                                 s = 80 mm = 0,08 m

                                                                 p.p. =  25 x 0,08 = 1,6 KN/mq 

• Controsoffitto in pannelli di gesso --> p.p. =0,35 KN/mq
• Incidenza impianti --> 0,1 KN/mq
• Incidenza tramezzi --> 1,60 KN/mq
•  

TOTALE CARICHI PERMANENTI = 4,05 KN/mq

 

CARICHI ACCIDENTALI

• Cat. A _ Civile abitazione --> 2 KN/mq

 

Combinazione di carico allo SLU per 1mq di solaio --> q = 2,42x1,3 + 4,05x1,5 + 2x1,5 = 12,22 KN/mq

Carico lineare agente sulla trave --> qu = qtot / l = q x i = 12,22 KN/mq x 3,5 m = 42,77 KN/m

E’ possibile determinare così il momento massimo della trave, considerando il modello semplice di mensola.

 Mmax = qu x l^2/2 = 42,77 x 4 / 2  = 85,55 KN*m

Scelto l’acciaio con cui si desidera realizzare la trave, in questo caso acciaio S275, si determinano la tensione caratteristica di snervamento fyk = 275 N/mmq e la tensione caratteristica di progetto fyd = fyk/1,05 = 261,90 N/mmq. 

Per il dimensionamento della sezione, si deve calcolare il valore minimo del modulo di resistenza a flessione affinché nessuna fibra del materiale super la tensione di progetto.

Wx,min = Mmax / fyd = 8555 KN*cm / 26,19 KN/cmq = 326,63 cmc

A questo punto dal sagomario si sceglie una trave IPE ingegnerizzata che abbia Wx > 326,63 cmc, cioè un IPE270 con Wx = 420,00 cmc.

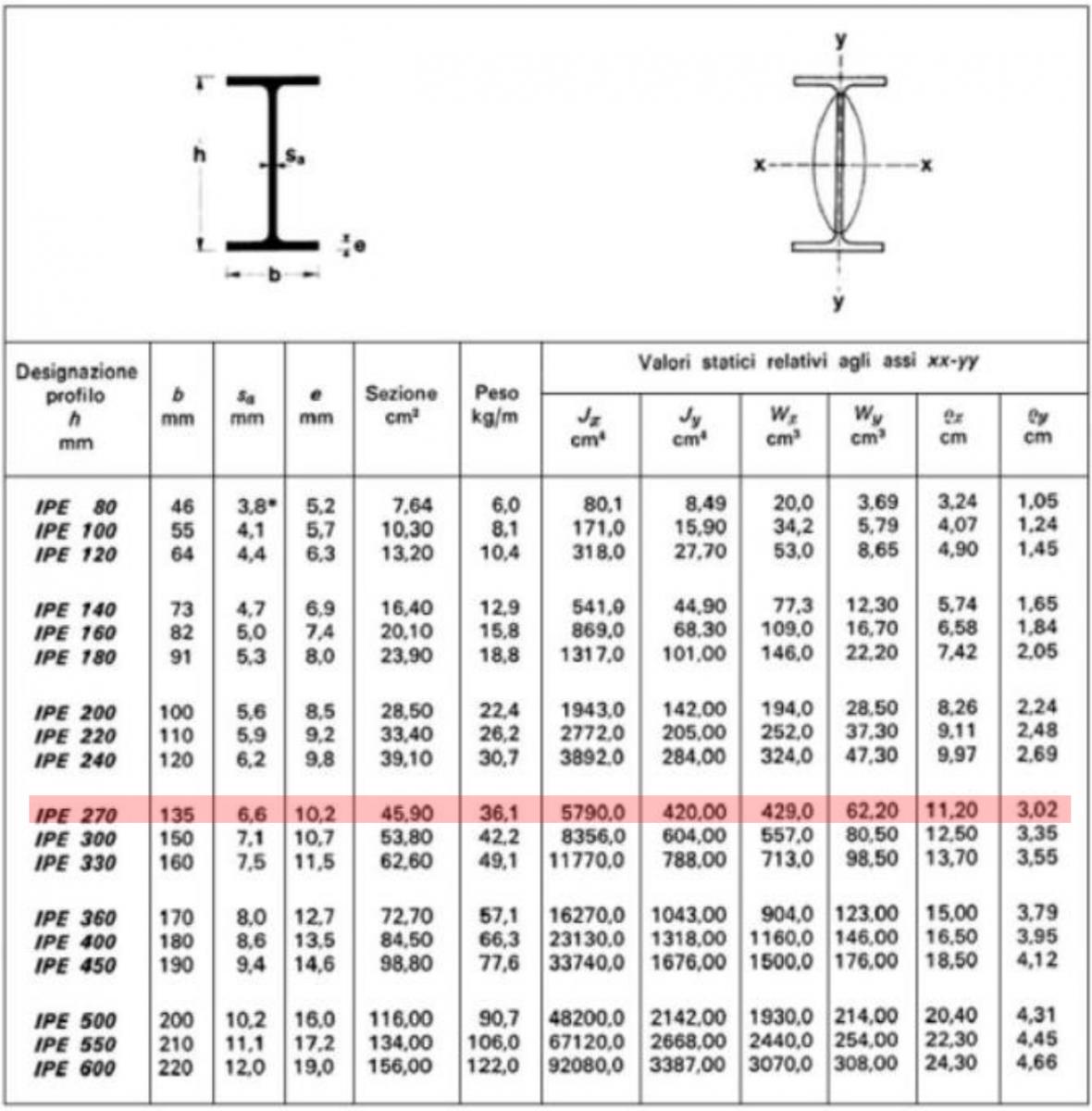
Conosciamo così il peso del profilo (0,361 kN/m), necessario per calcolare il carico totale:

qe = (G1 + G2 + psi 11 x Q1) x i + p.p. IPE270  = (2,42 + 4,05 + 0,5 x 2) x 3,5 + 0,361 = 26,5 kN/m

Infine il momento d’inerzia Ix (5790 cm^4 ) ed il modulo elastico E (210000 N/mmq)  dell’acciaio prescelto, consentono di stabilire lo spostamento della trave:

Vmax = qe x l^4 / 8 E Ix = 265 x (200)^4 / 8 x 21000000 x 5790 = 0,436 cm

La trave è verificata in quanto lo spostamento massimo soddisfa i requisiti della normativa. à 0,436 < 1/250 l = 200/250 = 0,8 cm.

Quanto eseguito è confermato dalla tabella di calcolo del foglio Excel.

 

CALCESTRUZZO ARMATO­

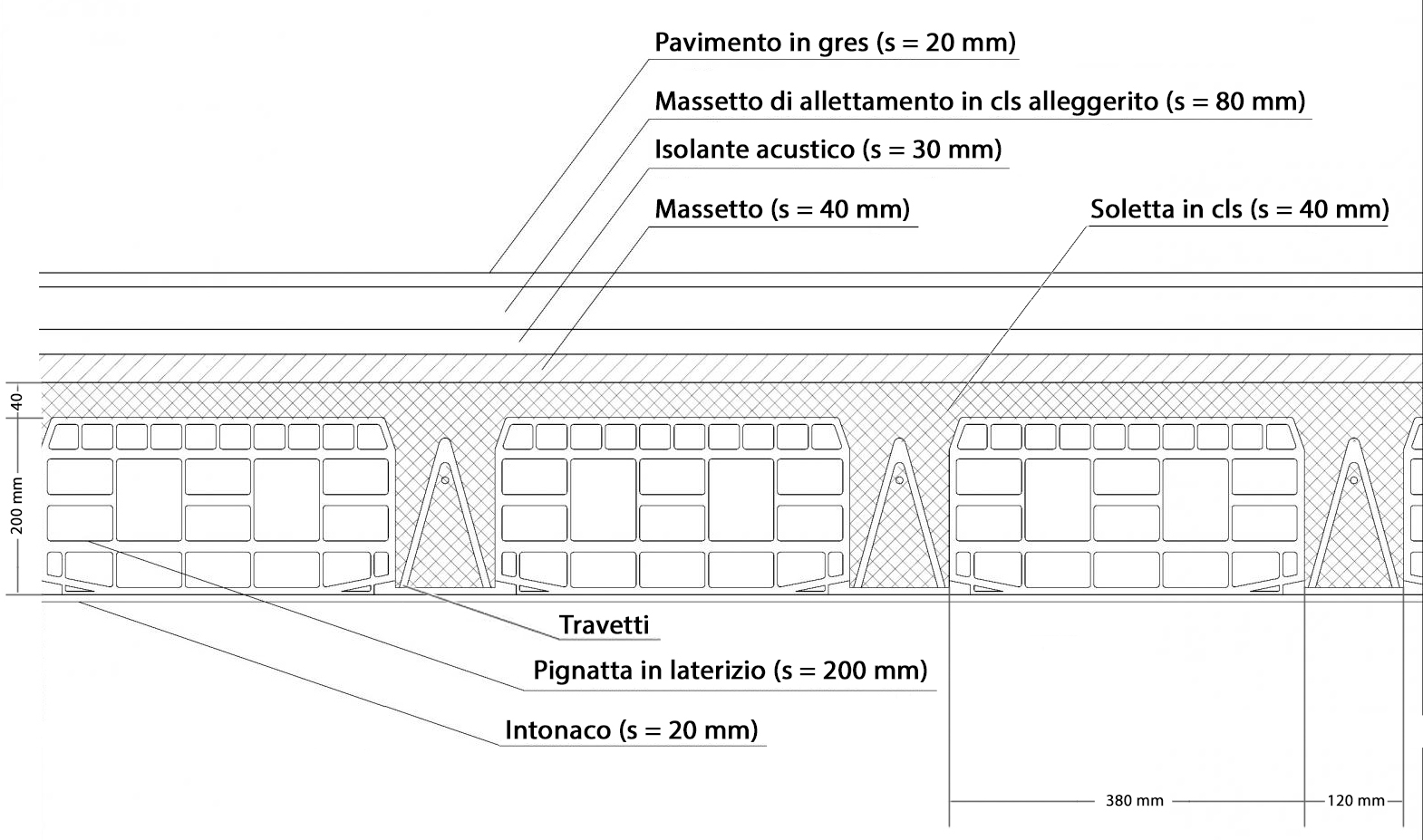
 CARICHI STRUTTURALI

• Soletta in cls --> γ = 25,00 KN/mc

                                       s = 40 mm = 0,04 m

                                        p.p. =  25 x 0,04 = 1 KN/mq

• Travetti --> γ = 25,00 KN/mc

                              Smedio = 0,12 x 0,2 / 0,50 = 0,048 m

                              p.p. =  25 x 0,048 = 1,20 KN/mq

• Pignatte -->  γ=8,00 KN/mc

                                Smedio = 0,38 x 0,2 / 0,50 = 0,152 m

                               p.p. =  8 x 0,152 = 1,22 KN/mq

TOTALE CARICHI STRUTTURALI = 3,42 KN/mq

 

CARICHI PERMANENTI

• Pavimento in gres (s = 20 mm)  --> p.p. =0,40 KN/mq
• Massetto di allettamento in cls alleggerito --> γ=20,00 KN/mc

                                                                                    s = 80 mm = 0,08 m

                                                                                    p.p. =  20 x 0,08 = 1,6 KN/mq 

• Isolante acustico (s = 30 mm) --> p.p. =0,30 KN/mq
• Massetto in malta di cemento --> γ=25,00 KN/mc

                                                                s = 40 mm = 0,04 m

                                                                p.p. =  25 x 0,04 = 1 KN/mq 

• Intonaco --> γ=18,00 KN/mc

                                s = 20 mm = 0,02 m

                                p.p. =18 x 0,02 = 0,36 KN/mq

• Incidenza impianti --> 0,5 KN/mq
• Incidenza tramezzi --> 1,60 KN/mq

TOTALE CARICHI PERMANENTI = 5,76 KN/mq

 

CARICHI ACCIDENTALI

• Cat. A _ Civile abitazione à 2 KN/mq

 

Combinazione di carico allo SLU per 1 mq di solaio --> q =3,42 x 1,3+5,76 x 1,5+2 x 1,5 = 16,09 KN/mq

Carico lineare agente sulla trave --> qu = qtot / l = q x i = 16,09 KN/mq x 3,5 m = 56,30 KN/m

Momento massimo della trave --> Mmax = qu x l^2/2 = 56,30 x 4 / 2 = 112,60 KN*m

Per il dimensionamento della sezione è necessario stabilire la resistenza caratteristica dell’acciaio (fyk = 450 N/mmq) e la resistenza caratteristica del calcestruzzo (fck = 45 N/mmq), dalle quali si ottengono:

• tensione di progetto dell’acciaio -->  fyd = fyk/1,15 = 391,30 N/mmq 
• tensione di progetto del cls compresso --> fcd = αcc x (fck / γc) = 0,85 x (45/1,5) = 25,5 N/mmq.

Impostando la dimensione della base (25 cm), è possibile ricavare l’altezza utile della sezione e successivamente l’altezza minima (34,25 cm), data dall’altezza utile sommata alla distanza tra il baricentro dell’armatura ed il filo del cls teso. Ingegnerizzando l’altezza minima (40 cm) si ottengono le dimensioni precise della sezione, verificate aggiungendo il peso proprio della trave.

                                           

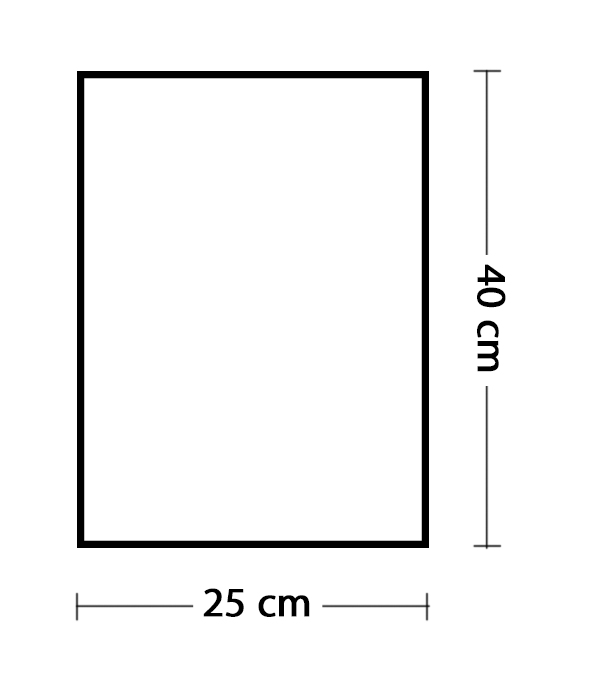
Trave --> γ = 25,00 KN/mc

                A = 0,25 m x 0,40 m = 0,1 mq

                p.p. = 25 x 0,1 = 2,50 KN/mq

Il peso proprio della trave viene utilizzato anche per calcolare il carico totale:

qe = (G1 + G2 + psi 11 x Q1) x i + p.p. trave  = (3,42 + 5,76 + 0,5 x 2) x 3,5 + 2,50 = 38,13 kN/m

Per stabilire lo spostamento della trave si calcola il momento d’inerzia di una sezione rettangolare:

 Ix = b x h^3 / 12 = 25 x 64000 / 12 = 133333 cm4

Quest’ ultimo insieme al modulo elastico E (210000 N/mmq)  dell’acciaio prescelto, consentono di stabilire lo spostamento della trave:

Vmax = qe x l^4 / 8 E Ix = 381,3 x (200)^4 / 8 x 21000000 x 133333 = 0,03 cm

La trave è verificata in quanto lo spostamento massimo soddisfa i requisiti della normativa. à 0,03 < 1/250 l = 200/250 = 0,8 cm.

Quanto eseguito è confermato dalla tabella di calcolo del foglio Excel._{­­­­­­­}

 

 

SOLAIO IN LEGNO

 

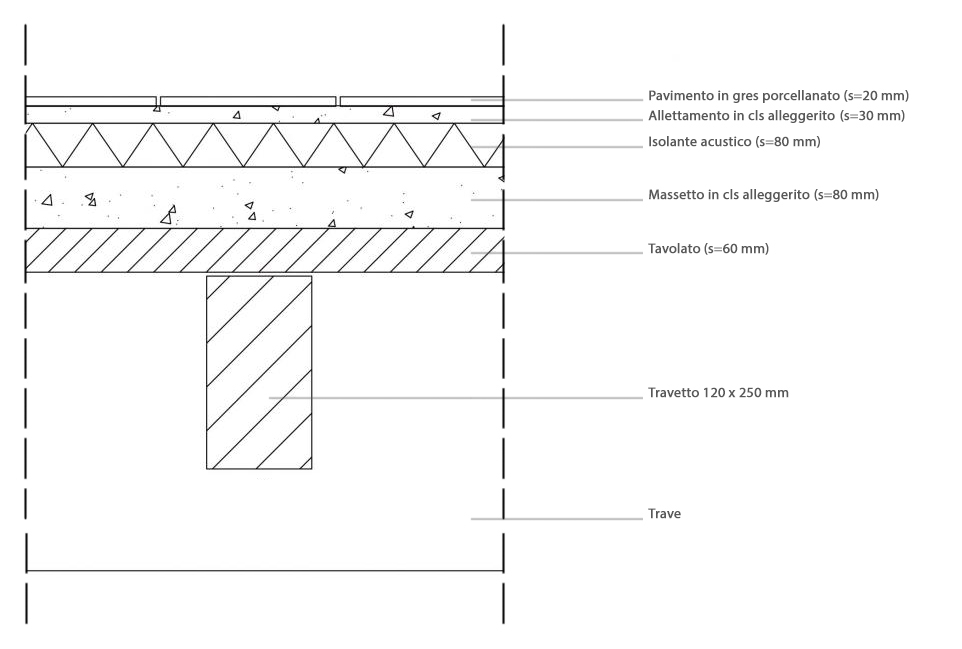
CARICHI STRUTTURALI

• Tavolato in legno d’ abete  -->  γ = 6,00 KN/mc

                                                             s = 60 mm = 0,06 m

                                                             p.p. =  6 x 0,06 = 0,36 KN/mq

• Travetti _ i = 1 m; l = 4m --> γ = 6,00 KN/mc

                                                         Volume = (0,12 m x 0,24 m x 1m) x 2 = 0,06 mc/mq

                                                         p.p. =  6 x 0,06 = 0,36 KN/mq

TOTALE CARICHI STRUTTURALI = 0,72 KN/mq

 

CARICHI PERMANENTI

• Pavimento in gres (s = 20 mm)  --> p.p. =0,40 KN/mq
• Massetto di allettamento in cls alleggerito  --> γ=20,00 KN/mc

                                                                                     s = 30 mm = 0,03 m

                                                                                     p.p. =  20 x 0,03 = 0,60 KN/mq 

• Isolante acustico in lana di vetro --> γ=0,6 KN/mc

                                                                     s = 80 mm = 0,08 m

                                                                     p.p. =0,048 KN/mq

• Massetto in cls alleggerito -->  γ=20,00 KN/mc

                                                            s = 80 mm = 0,08 m

                                                            p.p. = 20 x 0,08 = 1,6 KN/mq 

• Incidenza impianti --> 0,5 KN/mq
• Incidenza tramezzi --> 1 KN/mq

TOTALE CARICHI PERMANENTI = 4,15 KN/mq

 

CARICHI ACCIDENTALI

• Cat. A _ Civile abitazione à 2 KN/mq

 

Una volta determinati i carichi si svolgono gli stessi passaggi effettuati precedentemente, in modo tale da determinare il carico lineare agente sulla trave.

Combinazione di carico allo SLU per 1 mq di solaio --> q =0,72 x 1,3+4,15 x 1,5+2 x 1,5 = 10,16 KN/mq

Carico lineare agente sulla trave --> qu = qtot / l = q x i = 10,16 KN/mq x 3,5 m = 35,56 KN/m

Momento massimo della trave --> Mmax = qu x l^2/2 = 35,56 x 4 / 2 = 71,13 KN*m

Per il dimensionamento della sezione della trave bisogna indicare la resistenza caratteristica a flessione del legno da utilizzare, in questo caso fm,k = 24 N/mmq.

Per determinare la tensione di progetto, è necessario introdurre un coefficiente di sicurezza diminutivo dei valori di resistenza del materiale fornito dalla normativa; questo, oltre a dipendere dal tipo di materiale, tiene conto dell’effetto della durata del carico e delle condizioni di umidità in cui la struttura opererà. Per questo solaio si è scelto un legno lamellare di classe 1 con effetti di lunga durata, kmod = 0,7. Inoltre, viene utilizzato un altro coefficiente parziale di sicurezza relativo al materiale, γm = 1,45.                                                                                       

Tensione di progetto --> fdc = kmod x fm,k / γm = 0,7 x 24 [N/mmq] / 1,45 = 11,59 N/mmq

Impostando la dimensione della base (25 cm), è possibile ricavare l’altezza minima della sezione (38,38 cm) da ingegnerizzare (45 cm). Così si ottengono le dimensioni precise della sezione.

                                               

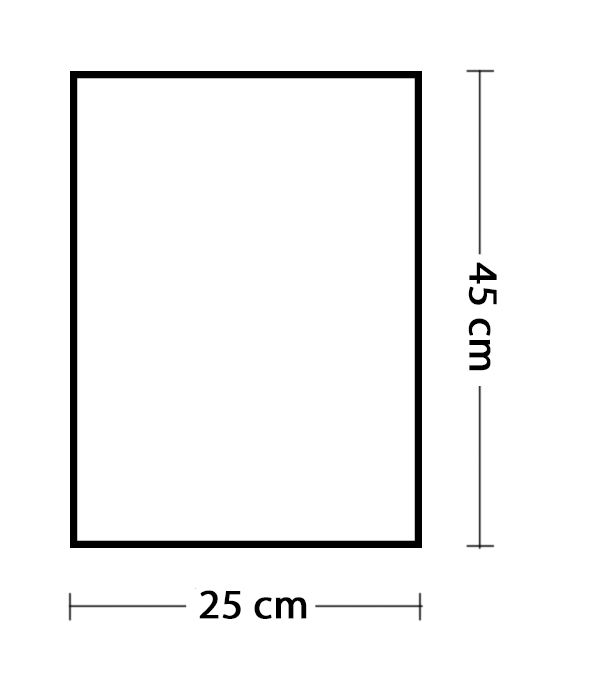
Per ottenere il carico totale allo SLE frequente il peso proprio della trave, a differenza dei casi precedenti, può essere trascurato in quanto il legno è un materiale leggero.

qe = (G1 + G2 + psi 11 x Q1) x i   = (0,72 + 4,15 + 0,5 x 2) x 3,5 = 20,55 kN/m

Per stabilire lo spostamento della trave si calcola il momento d’inerzia di una sezione rettangolare:

 Ix = b x h^3 / 12 = 25 x 91125 / 12 = 189844 cm4

Quest’ ultimo insieme al modulo elastico E (8000 N/mmq) del materiale, consentono di stabilire lo spostamento della trave:

Vmax = qe x l^4 / 8 E Ix = 205,5 x (200)^4 / 8 x 800000 x 189844 = 0,27 cm

La trave è verificata in quanto lo spostamento massimo soddisfa i requisiti della normativa. à 0,27 < 1/250 l = 200/250 = 0,8 cm.

Quanto eseguito è confermato dalla tabella di calcolo del foglio Excel._{­­­­­­­}

Per la seconda esercitazione dobbiamo occuparci del dimensionamento della trave di un solaio realizzato con tre tecnologie diverse: in legno, in acciaio e in calcestruzzo.

Scelto lo schema di un telaio piano con interasse variabile, dobbiamo innanzitutto, predimensionare le travi, in base alla luce e alla funzione che devono svolgere, cioè in base ai carichi che devono sostenere durante tutta la vita dell’opera.

Individuiamo quindi la gerarchia delle travi e l’area d’influenza della trave maggiormente sollecitata (con il maggior carico a metro lineare di trave), ricordandoci che a parità di area d’influenza si considera la trave con la luce maggiore.

Per ognuna delle tecnologie costruttive procediamo con l’analisi dei carichi agenti sul solaio, che si dividono in carichi strutturali - q_s -,  carichi permanenti - q_p - (azioni agenti sulla struttura) e carichi accidentali -q_a- (azioni agenti sulla struttura che variano sensibilmente nel tempo, queste azioni dipendono anche dalla destinazione d’uso dell’opera). Questi carichi vengono poi moltiplicati per dei coefficienti di combinazione, che aumentano il margine di sicurezza della struttura, che possiamo trovare nella normativa (NTC2008-Norme tecniche per le costruzioni – D.M. 14 Gennaio 2008). Hai fini della nostra esercitazione consideriamo la combinazione fondamentale allo stato limite ultimo.

 Andiamo ora a calcolare i vari carichi 

Solaio in cls:

Il solaio analizzato è in latero cemento armato, con destinazione residenziale

Peso proprio della struttura:

soletta in cemento armato _ 0,4 m · 25 KN/m³ = 1 KN/m² 

travetti _ 0,12 m (0,24 - 0,04)m · 25 KN/m³ = 1,2 KN/m²

pignatte _ 0,38 m (0,24 - 0,04)m · 6 KN/m³ = 0,92 KN/m²

q_s = 3,12 KN/m²

 

Peso portato dalla struttura:

pavimento piastrelle _ 0,02 m × 20 KN/m³ = 0,4 KN/m² 

allettamento _ 0,04 m · 20 KN/m³ = 0,8 KN/m² 

massetto _ 0,04 m · 18 KN/m³ = 0,72 KN/m² 

isolante _ 0,03 KN/m² 

intonaco _ 0,02 m · 20 KN/m³ = 0,4 KN/m² 

incidenza tramezzi  1,6 KN/m² 

q_p = 3,95 KN/m²

 

Carico accidentale:

cat A. – civile abitazione q_a  = 2,00 KN/m²

Calcoliamo il carico totale attraverso una tabella Exel

(KN/ m²(3,95 · 1,3) + (2,35 · 1,5) + (2,00 · 1,5)) 5,5 m = 64,13 KN/m = q_u

Possiamo ora procedere con il calcolo del momento massimo, che è dato dal prodotto del carico totale q_u per la luce al quadrato tutto diviso 8

M_max= ql²/8= 200,4 KNm

Una volta trovato il valore del momento massimo procediamo scegliendo il tipo di acciaio e di calcestruzzo determinando i valori delle tensioni di progetto del calcestruzzo f_cd e quella delle barre d’acciaio f_yd attraverso i valori della resistenza dei due materiali:

 f_cd = α_cc f_ck/g_c

f_yd = f_yk/g_m

Definendo ora la base della sezione e noti i valori delle tensioni di progetto calcoliamo l’altezza utile da sommare al copri ferro per ottenere l'altezza minima della sezione anche attraverso b r che sono rispettivamente

b= f_cd/ (f_cd+( f_yd/n))

r=(2/(f_cd(1-(b/3)b))^1/2

Il peso proprio della trave ci permette di verificare se la sezione da noi scelta è in grado di portare i carichi precedentemente calcolati. Per verificarlo dobbiamo sommare al carico totale q_u il peso proprio appena calcolato moltiplicato per il relativo fattore di sicurezza e rifare i calcoli. 

Se l'H_min dovesse risultare maggiore dell'H ingegnerizzata bisognerà rivedere l'altezza utile della sezione.

 

Solaio in legno:

Il solaio preso in esame è un solaio realizzato con travi principali con interasse maggiore pari a 5,5m con dei travetti 10x10cm disposti trasversalmente.

Analisi dei carichi

Peso proprio della struttura:

travetti _ (0,1 × 0,1 × 1)m 6 KN/m³ = 0,06 KN/m²

tavolato _ 0,03 m × 18 KN/m³ = 0,21 KN/m² 

q_s = 0,27 KN/m²

 

Peso portato dalla struttura:

parquet _ 0,02 m × 7,5 KN/m³ = 0,15 KN/m² 

sottofondo _ 0,03 m × 18 KN/m³ = 0,54 KN/m² 

caldana _ 0,04m × 21KN/m³ = 0,84 KN/m² 

incidenza tramezzi _ 1 KN/m² 

q_p = 2,74 KN/m²

 

Carico accidentale:

cat A. – civile abitazione q_p  = 2,00 KN/m²

Una volta calcolato il carico totale, troviamoci il momento massimo della nostra trave doppiamente appoggiata, sempre attraverso il foglio Excel.

M_max= ql²/8= 114,13 KNm

Procediamo inserendo il valore caratteristico a flessione del legno (che si differenzia da quello della resistenza a trazione o compressione, in quanto non è un materiale che reagisce allo stesso modo nelle diverse direzioni) scelto in base alla classe di resistenza. Nel  nostro caso utilizziamo il valore del legno lamellare.

La resistenza caratteristica del materiale f_mk insieme al coefficiente parziale di sicurezza del materiale γ_M e

 al coefficiente diminutivo del valore di resistenza k_mod, che tiene conto dell’effetto della durata del carico e delle condizioni in cui la struttura si andrà ad inserire, ci permettono di ricavare la tensione di progetto f_d, in base al materiale prescelto.  

Ricavata la tensione di progetto procediamo determinando una dimensione della base della sezione e andiamo a calcolare l’altezza minima:

 

Una volta trovata l’altezza minima la sezione va ingegnerizzata cioè va scelto un valore superiore all’altezza minima

che sia compatibile con i profili esistenti sul mercato.

La trave adottata avrà dimensioni 35x45 cm

 

Solaio in acciaio:

Analisi dei carichi

Peso proprio della struttura:

travetti secondari IPE 140 _ 12,9 Kg/m _ 0,129 KN/m²

lamiera grecata s=1 mm _ 13,08 Kg/m² = 0,13 KN/m² 

 

soletta in c.a. s = 0,065 + (0,055/2) = 0,0925 m _ 25 KN/m³ × 0,0925 = 2,31 KN/m² 

q_s = 2,55KN/m²

 

Peso portato dalla struttura:

pavimento piastrellato _ 0,02 m × 20 KN/m³ = 0,15 KN/m² 

massetto _ 0,1 m × 19 KN/m³ = 1,9 KN/m² 

controsoffitto _ 0,40 KN/m²

incidenza tramezzi _ 1 KN/m² 

q_p = 3,45 KN/m²

 

Carico accidentale:

cat A. – civile abitazione q_a  = 2,00 KN/m²

Una volta calcolato il carico e il momento massimo scegliamo il tipo di acciaio, nel nostro caso acciaio S275 che quindi avrà come tensione di snervamento caratteristica del materiale f_yk = 275 Mpa.  

Calcolata poi la tensione di progetto applichiamo la formula di Navier per ricavare il modulo di resistenza a flessione W_x. che ci serve per sapere il valore minimo che può avere la nostra sezione.

Andiamo ora sul sagomario e scegliamo un valore di resistenza maggiore e ingegnerizzato rispetto a quello trovato. 

La trave adottata sarà un IPE 330 

 

 

 

Obiettivo: dimensionare la trave più sollecitata di una carpenteria generica composta da telai piani che collaborano con pilastri.

Nel primo caso la carpenteria viene considerata in acciaio, la seconda in cls e la terza in legno.

Cme prima operazione scelgo la pianta di carpenteria di un edificio generico all'interno della quale individuo la trave maggiormente sollecitata , l'area di influenza e la lunghezza dell'interasse.

Luce= 5,00 m

Interasse=5,00 m

Area di influenza= 25,00 mq

 

ACCIAIO

Dopo aver individuato la trave che voglio dimensionare scelgo la tratigrafia del solaio in questione in modo da poterne valutare il peso.

a questo punto imposto una tabella excel che mi aiuti a calcolare il valore dei carichi strutturali, permanenti e accidentali.

Per far ciò introduco lo spessore dei vari elementi del solaio* (in mm), il peso specifico (in kN/mq) ed ottengo nella terza colonna il peso al mq impostando

spessore (mm) /1000 * peso specifico ( kN/mc) = peso al mq

identifico con il colore arancio i carichi strutturali, con il celeste quelli permanenti (fra coi includo un'ipotetica incidenza di impianti e tramezzi) e con il rosso quelli accidentali (da normativa): li sommo poi in base alla categoria.

Calcolo infine il Carico totale attraverso la formula:

qu= (qs*1,3 + qp*1,5 + qa*1,5) * interasse

dove 1,3 e 1,5 sono i coefficienti di sicurezza da normativa

*NB: talvolta ho calcolato spessori medi per ovviare al problema di elementi non uniformamente distribuiti sul solaio.

Calcolati i carichi che gravano sul solaio non mi resta che inserire i dati richiesti nella tabella che i permette di dimensionare la trave: inserisco la luce, l'interasse, i carichi appena individuati e la resistenza dell'acciaio ottenendo:

qu=(qs*1,3 + qp*1,5 + qa*1,5) * interasse

Mmax(kN*m) =ql²/8

fyd (N/mm2)= fyk/1,05

Wx,min (cm3) = Mmax / fyd*1000

scelgo il Wx in base al profilario

Procedo con la verifica, aggiungendo al carico totale il peso della trave che ho stimato essere di 0,48 kN per capire se essa è sufficiente.

la trave risulta verificata.

CLS ARMATO 

per il calcestruzzo utilizzerò lo stesso procedimento nell'individuazione dell'area di influenza e nel calcolo del peso del solaio che ho scelto.

inserisco i dati prodotti nella tabella precedentemente utilizzata per l'acciaio ed ottengo qs, qp ,qa e qu.

Dimensiono la trave con una tabella ad hoc in cui, impostando i dati e scegliendo una base ottengo l'altezza minima che la sezione dovrà avere 

anche aggiungendo il peso proprio della trave la sezione risulta verificata.

LEGNO

Come ultima prova ipotizzo che il solaio sia in legno, immaginando la seguente stratigrafia

 

calcolo nuovamente i carichi sul solaio con lo stesso metodo

 

trovati i dati li inserisco nella tabella del legno

sovradimensiono leggermente la trave per far si che la verifica sia soddisfatta.

Nb i coefficienti di sicurezza utilizzati per il legno sono più alti rispetto a quelli degli  altri materiali, questo dipende dalla diffidenza che la normativaprova al momento verso questo materiale. 

 

 

 

 

 

 

L'esercitazione consiste nel dimensionamento di una trave a sbalzo nei tre materiali: acciaio, c.a. e legno.

Disegno uno stralcio di un telaio piano definendo l'orditura del solaio.

 Individuo le travi principali e  quindi quella maggiormente sollecitata con la sua area d'influenza.

In tutte le tipologie la prima cosa da fare è calcolare i carichi strutturali, permanenti e accidentali in modo da ottenere la densità di carico qu agente sulla trave. A questo punto, a seconda della luce della trave,

possiamo ricavare il momento max che segue lo schema statico di una mensola, quindi: qul^2/2

Dopo aver dimensionato la sezione, bisogna effettuare la verifica di deformabilità della trave, controllando l'abbassamento max dell'elemento in rapporto alla sua luce. Quindi, come da normativa per i solai, devo verificare che la deformabilità della trave a sbalzo sia inferiore a 1/250 della sua luce. Per far ciò la verifica condotta è allo SLE (stato limite di esercizio) proprio perchè la verifica è finalizzata a controllare che non ci siano spostamenti e deformazioni che limitino  l'uso della costruzione e la sua efficienza.

Considero come carichi strutturali, permanenti e accidentali quelli dell'esercitazione precedente. Destinazione d'uso: civile abitazione.

SOLAIO IN ACCIAIO

Elementi che compongono il solaio

lamiera grecata Hi-Bond s=0,8mm

getto completamento c.a y=25,00 Kn/mc

massetto s=100mm y=20,00Kn/mc

Pavimento in gres ceramico s=20mm

Controsoffitto

Trave secondaria

Carichi strutturali qs

Peso proprio lamieta grecata= 10,47Kg/mq --> 0,11Kn/mq

Smedio getto di completamento= 92,5mm --> Peso proprio soletta= y x Smedio= 25,00 X 0,0925= 2,32 Kn/mq

qs= 2,43 Kn/mq

Carichi permanenti qp

 pavimento in gres ceramico= 0,40Kn/mq

massetto = y X s= 20,00 X 0,10 = 2Kn/mq

controsoffitto= 0,6Kn/mq

incidenza impianti= 0,10Kn/mq

incidenza tramezzi= 1,60Kn/mq

Carichi accidentali qa --> civile abitazione= 2,00Kn/mq

Determino la sezione: dopo aver trovato il valore del momento max, scelgo il tipo di acciaio, determino la tensione di progetto, trovo il valore minimo della resistenza a flessione--> scelgo il profilo.

 

Nella trave in acciaio bisogna bisogna tener conto del suo peso proprio che viene poi aggiunto automaticamente dalla tabella nel calcolo del carico totale qe (combinazione di carico frequente per SLE reversibili), necessario per il calcolo dello spostamento. 

Per calcolare lo spostamento bisogna infine conoscere il materiale, quindi il suo modulo elastico E e, la sua geometria, quindi il momento di inerzia Ix.

A questo punto è possibile calcolare l'abbassamento max e verificare che il rapporto tra la luce della trave e il suo spostamento max sia maggiore di 250, come da normativa.

                          

    

La sezione risulta verificata.

 

CEMENTO ARMATO

Elementi che compongono il solaio

Pavimento in gres s= 20mm

allettamento s=80mm

isolante acustico s=30mm

massetto s=40mm y=20,00Kn/mc

Pignatta laterizio= 380 X 200 mm i=500mm

travetti= 120mm

intonaco s=20mm

Carichi strutturali qs

 Peso proprio soletta 25,00 X 0,04= 1Kn/mq

Peso proprio travetti 25,00 X 0,12 X (0,24-0,04)/0,5= 1,20 Kn/mq

Peso proprio pignatte 6,00 X 0,38 X (0,24-0,04)/0,5= 0,92 Kn/mq

qs= 3,12Kn/mq

Carichi permanenti qp

Pavimento in gres ceramico= 0,4Kn/mq

Allettamento + massetto Stot=80+40=120mm-->0,12m -> 20,00 X 0,12= 2,4Kn/mq

Intonaco= 20,00 X 0,02= 0,40Kn/mq

Isolante=0,3Kn/mq

Incidenza tramezzi= 1,60Kn/mq

Incidenza impianti=0,10Kn/mq

qp=5,2Kn/mq

Carichi accidentali qa--> civile abitazione=2,00Kn/mq

Determino la sezione. La sezione viene determinata come l'esercitazione precedente, con l'unica differenza del momento max che tiene conto dello schema statico della mensola, come precedentemente specificato.

Materiali: acciaio S450 (armatura), cls C30. --> dai valori delle tensioni di progetto e dalla base scelta determino l'altezza utile da cui si determina l'altezza minima che tiene conto della distanza Delta tra il baricentro della trave e il filo teto del cls--> ingegnerizzo la sezione--> determino la geometria della sezione.

Il peso proprio della trave viene direttamente calcolato dalla tabella, conoscendo il peso specifico del cls (come precedente esercitazione).

Come per l'acciaio si calcola il carico totale qe (combinazione di carico frequente per SLE reversibili), necessario per il calcolo dello spostamento.  .

Determino E, il modulo elastico del materiale, e Ix, il momento d'inerzia (Ix=(b*h³)/12).

A questo punto è possibile calcolare l'abbassamento max e verificare che il rapporto tra la luce della trave e il suo spostamento max sia maggiore di 250, come da normativa.

                          

La sezione risulta verificata.

 

 

LEGNO

 

Elementi che compongono il solaio

Pavimento in gres ceramico

Allettamento s=20mm

Massetto s=40mm

tavolato s=30mm y=6Kn/mc

Travicelli 80X100mm y=6Kn/mc

Carichi strutturali qs

travicelli --> 6 X 2(0,1 X 0,08)= 0,096Kn/mq

tavolato--> 6 X 0,003= 0,18Kn/mq

qs=0,276

Carichi permanenti qp

massetto --> 20,00 X 0,04= 0,8 Kn/mq

allettamento--> 20,00 X 0,02= 0,4Kn/mq

pavimento= 0,4Kn/mq

incidenza impianti= 0,10Kn/mq

incidenza tramezzi= 1,60 Kn/mq

qp=3,3Kn/mq

Carichi accidentali qa --> civile avitazione=2,00Kn/mq

Determino la sezione--> dal carico al metro lineare trovo il momento max (qul^2/2)--> definisco il tipo di legno : legno massiccio di classe C24. Inserisco quindi la relativa resistenza caratteristica a flessione fm,k data dalla normativa e quindi la  tensione di progetto, che tiene conto anche del coefficiente diminutivo k.  Scelgo la vase della sezione per determinare un'altezza minima che viene poi ingegnerizzata.

Nel caso del legno il peso proprio viene trascurato (materiale leggero).

Come per l'acciaio e per il c.a. si calcola il carico totale qe (combinazione di carico frequente per SLE reversibili), necessario per il calcolo dello spostamento.  .

Determino E, il modulo elastico del materiale, e Ix, il momento d'inerzia (Ix=(b*h³)/12).

A questo punto è possibile calcolare l'abbassamento max e verificare che il rapporto tra la luce della trave e il suo spostamento max sia maggiore di 250, come da normativa.

                          

La sezione risulta verificata.

 

sciegliendo poi la larghezza della trave calcoleremo l'altezza min della nostra trave

hmin=√ M max / b x√ 6/ fd

Valore che verrà poi ingegnerizzato scegliento un valore subito maggiore a quello trovato e compatibile con i profilati sul mercato.

 

ACCIAIO

Per quanto riguarda la tecnologia dell'acciaio calcoleremo prima di tutto i nuovi valori di qs, qp e qa, corrispondenti ad un solaio in acciaio utilizzando lo stesso procedimento adottato per la tecnologia del legno

In questo caso il carico strutturale qs sarà composto dalla soletta con lamiera grecata

qs= 1,8 KN/mq

il carico permanente dato da pavimento, sottofondo di allettamento, isolante

qp= 1 KN/mq

e il carico permanente rimarrà qa= 2 KN/mq da normativa

Andiamo quindi a inserire i suddetti valori nel foglio di calcolo relativo all'acciaio

Essendo interasse e luce gia dati, il foglio calcolerà il momento massimo M max attraverso la formula

M max= ql^2/8

Scegliamo ora di utilizzare un acciaio con tensione caratteristica del materiale pari a 275 N/mm^2

Calcoleremo quindi la tensione di progetto attraverso la formula

fd= fy,k / ys

dove ys è per l'acciaio pari a 1,05

Calcoleremo quindi ora il modulo di resistenza a flessione minimo, ossia il valore minimo che la nostra trave dovrà assumere affinchè nessuna fibra superi la tensione di progetto

W x,min= M max/ fd

Questo valore andrà poi ingegnerizzato, ossia andrà scelto sulle tabelle dei profilati IPE il valore subito più grande, che corrisponderà alla sezione da noi richiesta

 

CALCESTRUZZO ARMATO

Affrontiamo infine l'ultima delle tre tecnologie, ossia il calcestruzzo armato.

Andremo quindi anche in questo caso a individuare il valore del carico gravante sulla trave

In questo caso il carico strutturale corrisponderà alle pignatte e alla soletta in cls per un totale 

qs= 0,61 KN/mq

il carico permanente sarà invece composto da sottofondo di allettamento, isolante, pavimento

qp=1,02 KN/mq

Infine riporto nuovamente il carico accidentale 

qa= 2KN/mq dato da normativa

Inseriamo quindi i nuovi valori nel foglio excell corrispondente al cls armato

Dati quindi interasse e luce della trave calcoleremo il momento massimo sempre attraverso la formula

M max= ql^2 / 8

A questo punto scegliamo l'acciaio che andrà a comporre le barre all'interno della nostra sezione e inseriamo la tensione caratteristica corrispondente. Calcoliamo così la tensione di progetto

fd= fyk/ ys

Allo stesso modo inseriamo la tensione caratteristica che corrisponde al calcestruzzo componente la nostra sezione

Calcoliamo così la tensione di progetto

fcd= acc x fck/ yc

Con acc che rappresenta il coefficente riduttivo per le resistenze di lunga durata, pari a 0,85; e yc, il coefficente parziale di sicurezza relativo al calcestruzzo, uguale a 1,5.

Ora fissando la lunghezza della base b della nostra sezione calcoleremo l'altezza utile della nostra sezione

hu=r √ M max/ b

dove r=√ 2/ fcd(1-beta/3)beta    e       beta=(fcd/ fcd + fyd x n)

All'altezza utile hu andrà poi sommato il copriferro c, ossia la distanza tra il baricentro dell'armatura e il filo del calcestruzzo teso

H min= hu + c

Otteniamo quindi il valore min dell'altezza della nostra sezione, che andrà poi ingegnerizzato scegliendo il valore subito più grande a quello dato.

Voglio dimensionare una trave a sbalzo di un impalcato nelle tre tecnologie: CLS armato, acciaio, legno.

Andiamo ad analizzare la pianta delle carpenterie:

La luce della trave è di 3,00 m e l'interasse è 3,50 m, calcolo così l'area di influenza della mensola, evidenziata in grigio che è 10,50 mq.

---

SOLAIO IN CLS ARMATO

Come nella precedente esercitazione andiamo a definire la composizione del solaio:

Anche in questo caso conosciamo l'interasse dei travetti, pari a 0,50 m, e quindi il valore di 1/i=2.

Dopo avere effettuato l'analisi dei carichi:

Procediamo con il dimensionamento attraverso il foglio excel.

In questo caso il primo valore che cambia è quello del Momento massimo: il valore di Mmax di una mensola è infatti pari a qul^2/2 nell'incastro.

Procedo con il progetto della trave, dopo aver scelto i materiali: Acciaio da armatura fyk:450 mPa e calcestruzzo ordinario con resistenza caratteristica fck=30 mPa:

fisso la base a 30 cm e ottengo un'altezza minima di 45,28, che ingegnerizzo a 50 cm.

Ora bisogna calcolare il peso proprio della trave e aggiungerlo ai carichi strutturali:

Controllo ora che la sezione risulti verificata:

La sezione 500x400 mm è verificata

Adesso devo controllare che l'abbassamento massimo sia minore di 1/250 della luce libera della trave (che è 3 metri).

La formula è: 

Devo quindi inserire alcune informazioni riguardo la geometria (Ix) e il materiale della sezione (E):

Calcolo il momento d'inerzia intorno all'asse x : bh^3/12, e inserisco il modulo di elasticità del calcestruzzo: 21000 mPa.

il rapporto l/vmax è >250, pertanto la sezione è verificata.

---

SOLAIO IN ACCIAIO

Dopo aver effettuato l'analisi dei carichi:

andiamo a dimensionare la trave:

è stata scelta una sezione IPE 330:

Anche in questo caso va effettuata la verifica dell'abbassamento massimo: La mensola infatti non deve deformarsi più di 1/250 della sua luce.

il rapporto tra la luce e il vmax è maggiore di 250, pertanto la sezione IPE 330x160 mm è verificata.

---

SOLAIO IN LEGNO

Dopo aver effettuato l'analisi dei carichi anche in questo caso in modo analogo alla precedente esercitazione:

Possiamo procedere con il dimensionamento della sezione:

Otteniamo così una trave rettangolare in legno lamellare Gl 36c con valore kmod pari a 0,7 (per carichi di durata lunga) di sezione 450x300 mm.

In questo caso però, diversamente dall'acciaio e dal legno, possiamo trascurare il peso proprio della trave nel calcolo dell'abbassamento massimo, in quanto il legno è un materiale leggero e il suo peso non apporta significative variazioni. 

Anche in questo caso il valore dell'abbassamento massimo supera 250, quindi la Sezione è verificata.

 

 

L’ esercitazione prevede il dimensionamento della trave più sollecitata di un solaio di carpenteria in tre diverse tecnologie: legno, acciaio e cemento armato. 

Ho scelto di disegnare una parte della pianta dell’edificio che dovremmo progettare, è per questo motivo che non ho un impalcato di tutte travi doppiamente appoggiate, ma ho le travi principali con un aggetto.Le luci delle travi principali e secondarie sono uguali, ma poiché quelle principali non sono travi doppiamente appoggiate a causa dell’aggetto, che ne modifica il valore del momento massimo, ho progettato le travi secondarie

.

Ora possiamo iniziare a compilare le tre tabelle Excel (sarà necessario utilizzarne tre diverse a seconda del materiale). Dopo aver individuato la trave maggiormente sollecitata, possiamo mettere in evidenza la sua area di influenza e misurare la lunghezza dell’interasse, primo valore richiesto dalla tabella Excel.

Per la progettazione della trave sarà necessario utilizzare tre fogli Excel differenti a seconda del materiale.

La trave maggiormente sollecitata ha una luce di 8m, e un interasse di 8m.

DIMENSIONAMENTO DI UNA TRAVE IN LEGNO A SEZIONE RETTANGOLARE

Consideriamo il peso specifico di ogni materiale che compone il solaio per poi calcolare i tre carichi (qs,qp,qa) agenti sulla trave.

Carico strutturale (qs)

-tavolato, (0,03 m x 1 m x 1 m) /mq x 7 KN/mc = 0,21 KN/mq

-travetti, 2(0,1 m x 0,14 m x1 m) /mq 6 KN/mq = 0,168 KN/mq

Qs = 0,21 KN/mq + 0,168 KN/mq = 0,378 KN/mq

Carico portato (qp)

-pavimento, 0,3 KN/mq

-massetto, (0,03 m x 1 m x 1 m) /mq x 19 KN/mc = 0,57 KN/mq

-allettamento, (0,06 m x 1 m x 1 m) /mq x 14 Kn/mc = 0,84 KN/mq

Qp = 0,3 KN/mq + 0,57 KN/mq + 0,84 KN/mq = 1,71 KN/mq

Carico accidentale (qa)

Prendendo la tabella dalla normativa ho ipotizzato un uso residenziale quindi ho:

Qa = 2 KN/mq

Compilo il foglio Excel con i tre carichi così da calcolare il qu, che è la somma dei tre carichi x dei coefficienti di sicurezza x l’interasse.

In seguito aggiungo la luce del solaio, in modo da ottenere il M_max.

Inserisco i dati relativi al tipo di legno scelto per la trave da progettare in modo tale da ottenere la tensione di progetto.

ed imposto una base di 40 cm ottenendo una H_min pari a 66,26 cm

.
Ingegnerizzo questa misura prendendo H = 70cm

 

DIMENSIONAMENTO DI UNA TRAVE IN ACCIAIO IPE S235

Il procedimento è simile a quello per il progetto della trave in legno, bisognerà quindi scegliere il tipo di acciaio. Anche qui sarà necessario considerare il peso specifico di ogni materiale che compone il solaio e quindi calcolare i tre carichi agenti sulla trave. 

.

Carico strutturale (qs)

- IPE 200: 2 (0,00285 mq x 1 m) / 78,5 KN/mc = 0,447 KN/mq

- Getto in calcestruzzo e lamiera grecata: (21 kN/mc x 0,075 mc) / 1 mq = 1,86 KN/mq

Qs = 0,447 kN/mq + 1,86 kN/mq = 2,307 kN/mq

Carico permanente (qp)

-pavimento, 0,3 KN/mq

-massetto, (0,03 m x 1 m x 1 m) /mq x 19 KN/mc = 0,57 KN/mq

-isolante, (0,06 m x 1 m x 1 m) /mq x 14 Kn/mc = 0,84 KN/mq

Qp = 0,3 KN/mq +  0,57 KN/mq + 0,84 KN/mq = 1,71 KN/mq

Carico accidentale (qa)

Anche qui ho ipotizzato un uso residenziale, seguendo la tabella della normativa quindi ho:

Qa = 2 KN/mq

Compilo il foglio Excel con i tre carichi così da calcolare il qu (la somma dei tre carichi moltiplicati per dei coefficienti di sicurezza x l’interasse).

L’impalcato è lo stesso che ho utilizzato per il dimensionamento della trave in legno, quindi mantengo lo stesso interasse di 8 m e la luce di 8. In più devo assegnare un tipo di acciaio: S235. Con i dati assegnati, il file mi calcola automaticamente il M_max e fd, così da ottenere un Wx minimo.

Scelgo quindi dalla tabella dei profilati IPE la sezione con un Wx maggiore.

Ho scelto una IPE 600x220

 

 

DIMENSIONAMENTO  DI UNA TRAVE IN CEMENTO ARMATO

 

Ancora una volta procedimento è simile a quello per il progetto delle travi precedenti. Calcolo quindi i carichi agenti sul solaio.

Carico strutturale (qs)

 

- soletta collaborante :                      (0,04m x 1m x 1m)/mq x 24KN/mc = 0,96 KN/mq
- travetti:                                        2(0,10m x 0,16m x 1m)/mq x 24KN/mc = 0,768 KN/mq
- pignatta:                                       8 x 9,1 Kg/mq = 72,8 Kg/mq = 0,728 KN/mq

Q_s = (0,96 + 0,768 + 0,728 ) KN/mq = 2,456 KN/mq

 

Carico permanente (qp)

 

- pavimento in cotto:                        24Kg/mq = 0,24KN/mq
- malta di sottofondo:                       (0,02m x 1m x 1m)/mq x 18KN/mc = 0,36KN/mq
- strato di allettamento in cls             (0,03m x 1m x 1m)/mq x 24KN/mc= 0,72KN/mq
- isolante in lana di vetro                  (0,08m x 1m x 1m)/mq x 0,2KN/mc = 0,016KN/mq
- massetto delle pendenze                 (0,04m x 1m x 1m)/mq x 18KN/mc = 0,72KN/mq                                              - -intonaco                                       (0,01m x 1m x 1m)/mq x 13KN/mc = 0,13KN/mq

Q_p= (0,24 + 0,36 + 0,72 + 0,016 + 0,72 + 0,13 ) KN/mq = 2,186 KN/mq

 

 

Carico accidentale (qa)

Anche qui ho ipotizzato un uso residenziale, seguendo la tabella della normativa quindi ho:

Qa = 2 KN/mq

Ora anche per il calcestruzzo armato posso compilare il foglio Excel con i tre carichi così da calcolare il qu.

Dopo aver inserito nel file anche la luce, viene calcolato automaticamente il Mmax agente sulla trave. In seguito imposto le proprietà sia dell’acciaio (fyk) che del calcestruzzo (fck) che vengono automaticamente moltiplicati per i loro coefficienti di sicurezza (1,15 e 1,5).

Essendo la trave composta da due materiali diversi, le proprietà del materiale devono essere omogenizzate secondo un coefficiente (n=15) in modo da ottenere ß e r. 

Ora posso impostare la larghezza della trave (b=35 cm) così Excel mi calcola direttamente l’altezza utile della trave, che sommata alla distanza dal baricentro del ferro teso al lembo teso (δ=4) e mi da l’altezza minima

L’altezza minima è 51,11 cm, che ingegnerizzo scegliendo una sezione alta 55 cm.

A questo punto è possibile ottenere il peso unitario della trave; 

automaticamente quindi Excel svolge un’altra volta tutta la riga con i nuovi dati (è cambiato il qu) così posso sapere se la trave progettata è verificata o meno.

È verificata!