Esercitazione

Disegniamo la geometria 

SAP2000 è un programma che utilizza il metodo degli elementi finiti e si basa sulla Teoria di Eulero-Bernoulli. Per le unità di misura lavora con gruppi prestabiliti e  per questa esercitazione utilizzeremo kN,m,°C.

Per quanto riguarda gli assi utilizzeremo come ordinata z = gravità mentre come gli assi locali si decide tramite regola della mano destra:

                                                                       

Il programma ci permette di creare una struttura reticolare cubica o piramidale. Noi disegneremo quella cubica con:

1. New Model – Grid Only

Assi Locali:

X =3 m

Y =5 m

Z =2 m

Spazio Griglia:

X =2 m

Y =2 m

Z =2 m

           

2. Tasto Frame (per disegnare i lati e le diagonali del cubo)

Importante

-Prima di andare avanti con la struttura bisogna verificare che le aste non siano doppie:

Selezionare struttura – Edit –Merge Duplicates – OK

-Controllare che tutti i nodi siano uniti:

Selezionare la struttura – Edit – Edit Points - Merge Joints – 0,1 - OK

(0,1 = raggio entro cui tutti i nodi vicini coincidono nello stesso nodo)

Vincoli esterni

Vincoliamo esternamente la struttura con quattro cerniere agli spigoli esterni e assegniamo i vincoli interni alle aste:

-Assign – Joint – Restraints – selezionare la cerniera – OK

-Selezionare la struttura - Assign – Frame – Releases (accendere Moment 2-2 e 3-3) e ricontrollare l’unità di misura

          

          

Scelta del Profilo:

Selezionare la struttura – Assign – Frame – Frame Sections – Add New Property – Pipe Section – OK

           

 

Forze Concentrate

Dopo aver deciso di realizzare la struttura con dei tubolari in acciaio, l’ho caricata superiormente, con carichi di 50kN:

- Creare F ed eliminare il peso proprio:

Define – Load Patterns – “F” – (non considerare il peso proprio quindi scrivere 0 su "Self Weight Multiplier”) - cliccare su Add New Load Pattern – Selezionare il carico “F” – OK

- Assegnare il Carico 50kN:

Selezionare la parte superiore sella struttura – Assign – Joint Loads – Forces – Scegliere il carico F – Force Global Z – inserire –50kN – OK

          

 

Analisi della struttura - deformata

A questo punto, clicco Play per far partire l’analisi della struttura. Come vediamo dall’immagine la struttura si è deformata a causa del carico che ho ipotizzato dato che non ho considerato il peso proprio della struttura:

           

Analisi della struttura – sforzi normali

       

Tabella

Il programma SAP2000 riassume in una tabella tutti i valori che ho inserito e i relativi risultati. Il valore che ci interesserà  è lo Sforzo Normale (N) di ogni singola asta. Con SAP è possibile estrarre la tabella in formato Excel, così da facilitare i calcoli in seguito:

Display – Show Tables – Analysis Results – selezionare Select Load Patters, il carico F –Ok – Element Forces – Frames – File – Export Curren Table –To Excel – Labels – OK

Il sistema della tabella è molto semplice bisogna eliminare i valori che non vengono impiegati per il calcolo e lasciare:

lo sforzo normale = N

il numero delle aste = n°

le lunghezze delle aste = L

Dato che abbiamo scelto un cubo dobbiamo considerare solo le lunghezze di

 L=2 m (lati)

 L=2,82843 m (diagonali)

 

Dividiamo le Aste

Aste Tese _ Fase di Progetto

Prima cosa da fare è scegliere il tipo di acciaio dalla Normativa Tecnica per le costruzione – del 2008 ed identificare:

• La resistenza a tensione di snervamento fyk = 235MPa (Acciaio Classe Fe 360/S235);
• Il Coefficiente di sicurezza del materiale γm = 1,05
• Calcolare la resistenza a tensione di progetto: fyd (MPa) = fyk/γ

Calcolare l’area minima che deve avere l’elemento: A_min = N/fd

Scegliamo dalla Tabella Profilati metallici (scaricabile dal sito Profili Acciaio) i profili con:

A_design > A_min

Per le aste a trazione ho scelto 3 tipi di profilati in acciaio:

A=2,54 cm² - 33,7 x 2,6 mm

A=3,94 cm² - 42,4 x 3,2 mm

A=5,74 cm² - 60,3 x 3,2 mm

Fase di verifica _ σ<fd o N/A<fd

Consideriamo l’asta più sollecitata:

N/A = 126130 N / 574 mm² = 219,73 N/mm²   

fd = 223,81MPa

                                                                              N/A≤fd è VERIFICATA!

Asta Compressa _ Fase di Progetto

1 Fase di Progetto _ I calcoli per trovare A_min in un asta a compressione sono uguali come per l’asta a trazione:

• La resistenza a tensione di snervamento fyk = 235MPa (Acciaio Classe Fe 360/S235);
• Coefficiente di sicurezza del materiale γm=1,05;
• Calcolare la resistenza a tensione di progetto: fyd (MPa) = fyk/γ
• Calcolare l’area minima che deve avere l’elemento: A_min=N/fd

Per l’asta a compressione non basta la verifica dell’A_min, anzi bisogna considerare oltre alla rottura dell’asta anche lo sbandamento.

2 Fase di Progetto  _ Per questo bisogna considerare:

• Il modulo di elasticità del materiale E = 210000 MPa (acciaio);
• Lunghezza dell’asta l = 2m;
• Coefficiente del vincolo β= 1;
• Coefficiente di sicurezza del materiale γm=1,05;
• Sforzo Normale di progetto euleriano (kN) N_ed = N x γ
• Momento d’inerzia minimo (cm⁴) I_min = N_ed x (β x l)²/ π² x E

1-2 Fase di progetto_ Scegliere dalla Tabella dei Profili metallici:

• L’area di Progetto (cm²) A_design > A_min;
• Momento d’inerzia di progetto (cm⁴) I_design > I_min;
• Scrivere il raggio d’inerzia (cm)  ρ_design del profilo;
• Nell’asta di compressione bisogna conoscere la SNELLEZZA λ

Fase di Verifica  _ N/A < fd e λ ≤ 200

Asta n°67 più sollecitata

1- Come per l’asta a trazione verifichiamo anche per quella a compressione la più sollecitata:

N/A = -157445 N / 820 mm² = 192,0 N/mm²   

fd = 223,81MPa

                                                                             N/A≤fd è VERIFICATA!

2- Verifichiamo la snellezza λ ≤ 200 considerando sempre la stessa asta:

λ = 110,06

                                                                             λ ≤ 200 è VERIFICATA!

 

Per il dimensionamento di aste d’acciaio di una struttura reticolare il procedimento utilizzato prevede come primo passo di disegnare su SAP una griglia 3mx3m nella quale inserire la mia struttura reticolare, avendo cura di intelaiarla. Inserisco successivamente ai vertici il vincoli di cerniera esterni ed interni.

Proseguo scegliendo la sezione più consona delle travi (nel caso specifico tubolare in acciaio) e assegnando le forze, alle quali attribuisco arbitrariamente il valore di -150 kN.

                             

A questo punto posso avviare l’analisi che  produrrà una serie di risultati che esporterò su un foglio excell, il quale una volta “pulito” dei risultati inutili al fine dell’esercitazione e messo in ordine, apparirà così:

dove possiamo leggere tutte le aste in trazione e compressione, ed evidenziate in giallo le aste diagonali (dato che ci sarà utile successivamente nel calcolo delle aste in compressione).

Sul foglio excell fornitoci ora procedo per prima cosa con le aste in trazione, aggiornando, asta per asta, il mio sforzo N espresso in kN.

Dato il valore della tensione caratteristica di snervamento dell’acciaio f_yk e attribuito il coefficiente di sicurezza ϒ_m , si può trovare f_d , tensione di progetto, facendo f_yk / ϒ_m . A questo punto l’area minima sarà determinata da N / f_d , con l’accortezza di eseguire la giusta equivalenza in quanto espressa in cm². 

Infine l’ultima colonna sarà dedicata all’inserimento dei valori dell’area di design ricavata dalle tabelle dei profilati in base all’area min ottenuta. Ad esempio qui sotto il profilato più piccolo della tabella associato ai primi risultati ottenuti.

Proseguendo con le aste in compressione vado ad inserire i valori di N. I valori di f_yk, ϒ_m e f_d rimangono invariati rispetto al procedimento precedente, elaborando immediatamente l’area min. A questo punto però per le aste in compressione vanno fatti dei calcoli aggiuntivi che prevedono: l’inserimento del modulo di elasticità E, il valore β, pari ad 1 (in quanto siamo nel caso dell’asta appoggiata-appoggiata), la luce (che dovrà tener conto delle aste diagonali, misurate come l*√2), il ϒ_m, ed infine il calcolo dell’inerzia minima.

Infine in base ai risultati ottenuti andiamo ad ingegnerizzare l’area, l’inerzia e ρ (raggio d’inerzia minima). Ultimo dato ricavato sarà la snellezza, che tiene conto del raggio d’inerzia minima e della luce, secondo la relazione λ= l/ ρ.

La travatura reticolare è una struttura composta da un insieme di aste vincolate ai nodi, in modo da costituire un elemento resistente in grado di superare luci molto grandi. È formata da due elementi continui chiamati correnti, uno superiore e uno inferiore, collegati da altri elementi disposti alcuni in verticale e altri inclinati. Gli elementi verticali vengono denominati montanti, quelli inclinati diagonali. 
Questa seconda esercitazione prevede dunque la modellazione in tre dimensioni di una travatura reticolare, sui cui nodi superiori vengono applicati dei carichi concentrati, al fine di analizzare la deformazione e fare la verifica a sforzo normale. Essendo le travi reticolari sollecitate solo a sforzo normale, non troveremo sollecitazioni di taglio e momento. Il disegno tridimensionale della travatura può avvenire su cad o rhino, importandolo poi in sap, oppure direttamente su sap, preimpostando una griglia. Scelgo quest’ultimo metodo, quindi mi costruisco la griglia andando su File->New Model->Grid Only

Impostata la griglia, ricalco con Draw Frame un cubetto di dimensioni 2x2x2, controventato su ogni faccia con una diagonale, che poi ripeto per tutta la griglia. Questo è il risultato.

Adesso devo assegnare i vincoli ai quattro punti in basso all’estremità della griglia, e scelgo delle cerniere, andando su Assign->Joint->Restraints

Trasformo poi le aste della travatura in aste incernerate al loro interno, selezionando tutto, andando su

Assign->Frame->Releases/Partial Fixity e spuntando Moment 22 (minor) e Moment 33 (major).

Il passo successivo è quello di assegnare una sezione alla travatura reticolare, ad esempio una sezione tubolare, che rinomino “pipe”: Assign->Frame->Frame Section

 

Ora stabilisco i carichi concentrati che andrò ad applicare sui nodi superiori della travatura: su Define->Load patterns aggiungo un modello di carico che chiamo “F” e, dopo aver selezionato la fascia superiore della travatura: Assign->Joint Loads->Forces. In questo modo assegno il valore di carico che ho stabilito, ovvero di 80 KN verso il basso lungo l’asse verticale z.

Posso a questo punto avviare l’analisi (Run Analysis), ottenendo la deformata derivante dal carico da me stabilito.

Visualizziamo il grafico dello sforzo normale andando su Frames/Cables/Tendons e spuntando Axial Forces, e mettiamolo a confronto con i diagrammi dello sforzo di taglio e del momento, che essendo nulli, non di segnano alcun grafico.

Per visualizzare i risultati dello sforzo normale di trazione e di compressione a cui le aste sono soggette, si va su Display->Show Tables e spunto la casella Analysis Results, specificando che siano i risultati derivanti dal carico F che ho applicato inizialmente. Mi si apre così la finestra dei risultati, dove imposto la voce Element Forces Frames.

Ottenendo il valore dello sforzo normale per ogni singola asta, posso esportare il foglio dei dati su un documento di calcolo excel e procedere con il dimensionamento delle aste. 
Avendo inizialmente impostato una lunghezza delle aste pari a 2*2*2, sotto la colonna “station” troverò due dimensioni: 2m per le aste dritte e 2,82843m per le diagonali.

Come passo successivo mi riordino la colonna degli sforzi normali di trazione (+) e compressione (-)  dal più piccolo al più grande, in modo tale da copiare i valori positivi nel foglio di dimensionamento a trazione e quelli negativi nel foglio di dimensionamento a compressione.

ACCIAIO ASTA RETICOLARE-TRAZIONE

Scelta la tipologia di acciaio, in questo caso S275, con una resistenza caratteristica di 275 MPA, trovo la resistenza di progetto, dividendo la resistenza caratteristica per il coefficiente di sicurezza 1,05 (fyd=fyk/1,05). Dopodichè facendo il rapporto tra lo sforzo normale e la resistenza di progetto, posso conoscere l’area minima che l’asta deve avere per potere resistere alla sollecitazione (Amin=N/fyd). Andando sulla tabella dei profilati metallici cerco un sezione circolare >/= all’area minima calcolata.

Per esempio se prendo in considerazione la prima riga, avendo un’area minima di 24,06 cm2 trovo sul profilario un’area superiore pari a 39,50 relativa al profilo 219*5,9 (mm).

Chiaramente avendo in tutto 366 aste, 171 per quelle tese e 194 per quelle compresse, non attribuirò a ciascuna  un profilo diverso, bensì quattro-cinque profili, a ognuno dei quali corrisponderà un intervallo di valori più o meno ampio. Alla fine allegherò le  intere pagine calcolate per la trazione e per la compressione. Qui proseguo nel mostrare giusto qualche esempio utile ai fini della spiegazione.

ACCIAIO ASTA RETICOLARE-COMPRESSIONE

Mantenuto l’acciaio S275 e calcolata prima la resistenza di progetto e poi l’area minima, seguendo lo stesso procedimento della trazione, per trovare l’area di progetto devo prendere in considerazioni più elementi, poichè un’asta soggetta compressione è esposta non solo alla crisi di rottura, ma anche a quella dello sbandamento, ovvero quando presenta una configurazione non rettilinea. Quest’ultimo fenomeno si verifica quando il carico raggiunge una soglia massima e l’oggetto in questione è piuttosto snello (snellezza λ=lunghezza libera d’inflessione l0/raggio d’inerzia ρ ). Ecco quindi che entrano in gioco altri parametri, dal momento che per progettare un’asta compressa si necessita di AREA e di INERZIA.
-Lunghezza asta
-Modulo di elasticita: E=210000 MPa
-Coefficiente di vincolo che ci dice come sbanda l’asta: β = 1
-Snellezza asta: l0/ρ = λ =  π √E/√fcd
-Raggio d’inerzia: ρ = l0/λ
-Momento d’inerzia: I = A*(ρ)2

In particolare effettuo il dimensionamento considerando il momento d’inerzia e il raggio d’inerzia.

Prendendo come esempio la prima riga, con un’area minima di 33,90 cm2, un raggio d’inerzia minimo di 3,18 cm e un momento d’inerzia minimo di 343 cm4, ho considerato sempre il profilo 219*5,9 (mm), notando che I_design=2247>I_min=343, che rho_min_design=7,54>rho_min=3,18 e che A_design=39,5>A_min=33,90.

 

Allegherò in seguito due file PDF riguardanti le tabelle excel di tutte le aste sia tese che compresse con relativi 5 profilati metallici scelti, in modo da fornire eventuale approfondimento a chi interessato e mi scuso per l'ordine talvolta "creativo" della numerazione dei punti dove ho notato ripetersi due volte 4. e il salto del punto 12. (saltati solo nell'elencazione ma non nella storyboard)

 

La terza esercitazione riguarda il dimensionamento di una trave a sbalzo, usando un foglio di calcolo elettronico Excel, con tre tecnologie diverse:

- cemento armato
- legno
- acciaio.

Per il progetto del solaio, con ognuna di queste tre tecnologie, considero un’unica pianta di carpenteria:

La prima la posso utilizzare per rappresentare il solaio in legno ed in cemento armato, mentre la seconda riguarda la tecnologia dell’acciaio. La trave a sbalzo più sollecitata è quella lungo l’asse B, per questo motivo procedo con il dimensionamento di quest’ultima, che ha interasse 4m e luce 3m:

Il foglio elettronico che adesso andremo a compilare sarà diviso in due parti. Una prima parte sarà identico al foglio della prima esercitazione, quindi ragioniamo in termini di SLU poichè otteniamo una h_min tramite il q_u. Mentre la seconda parte, quella che riguarda questa nuova esercitazione, ragiona in termini di SLE in quanto dal q_e ottengo il dato relativo al v_max.
Ovviamente queste analisi presuppongono coefficienti di sicurezza diversi, poichè con l’analisi allo stato limite ultimo consideriamo lo stato più grave del danno, ovvero il collasso; mentre con l’analisi allo stato limite elastico consideriamo dei fenomeni come la deformabilità del solaio o la vibrazione di quest’utimo, quindi fenomeni che non compromettono il funzionamento generale della struttura ma arrecano fastidio agli occupanti di essa.
Ricordiamoci che adesso non stiamo più considerando il modello meccanico della trave appoggiata appoggiata, ma quello di una mensola. Quindi il M_max = (ql^2)/2
Procedo con l’analisi dell’abbassamento della trave nelle tre diverse tecnologie.

CEMENTO ARMATO

Come solaio e carichi di riferimento considero la mia prima esercitazione postata su questo blog (http://design.rootiers.it/strutture/node/1681). Per il cemento armato il calcolo del  q_u:
qu = (1,3qs + 1,5qp + 1,5qa) x interasse = 46,82 KN/m 
Mentre il M_max:
M_max = (ql^2)/2 = 210,7 KN/m
Impostando i dati relativi al materiale scelto (f_yk ed f_ck) ottengo per una base di 30 cm un'altezza minima di 54,10 cm che ingegnerizzo ad 60 cm. La trave ipotizzata ha un peso unitario di 4,5 KN/m, che va a sommarsi ai carichi e va a confermare la trave progettata: 
Adesso inizia la parte relativa allo SLE, poichè il foglio si calcola il q_e:
q_e = (1qs + 1qp + 0,5qa) x interasse = 33,02 KN/m
Imposto il Modulo elastico del c.a. pari a 21000 MPa ed ottengo una I_x:
I_x = (b*h^3)/12 = 540000cm⁴
Come risultato avrò un v_max = 0,29 cm, dato che mi conferma il progetto poichè I_x/ v_max >250

LEGNO

Come solaio e carichi di riferimento considero la mia prima esercitazione postata su questo blog (http://design.rootiers.it/strutture/node/1681). Per il legno il calcolo del  q_u:
qu = (1,3qs + 1,5qp + 1,5qa) x interasse = 31,60 KN/m 
Mentre il M_max:
M_max = (ql^2)/2 = 142,20 KN/m
Impostando i dati relativi al materiale scelto (f_mk) ottengo per una base di 30 cm un'altezza minima di 54,43 cm che ingegnerizzo ad 60 cm. A differenza del c.a. non considera il peso della trave progettata poichè il legno è un materiale leggero.

Adesso inizia la parte relativa allo SLE, poichè il foglio si calcola il q_e:
q_e = (1qs + 1qp + 0,5qa) x interasse = 19,00 KN/m
Imposto il Modulo elastico del c.a. pari a 8000 MPa ed ottengo una I_x:
I_x = (b*h^3)/12 = 540000cm⁴
Come risultato avrò un v_max = 0,45 cm, dato che mi conferma il progetto poichè I_x/ v_max >250

ACCIAIO
Come solaio e carichi di riferimento considero la mia prima esercitazione postata su questo blog (http://design.rootiers.it/strutture/node/1681). Per l'acciaio il calcolo del  q_u:
qu = (1,3qs + 1,5qp + 1,5qa) x interasse = 46,04 KN/m 
Mentre il M_max:
M_max = (ql^2)/2 = 207,20 KN/m
Impostando i dati relativi al materiale scelto (f_yk) ottengo W_x,min:
W_x,min = (M_max/ f_d)*1000 = 928,78 cm³

Scelgo il mio profilato ingegnerizzando quest'ultimo dato, avendo così un IPE 400

Inserisco sul foglio Excel i dati relativi al I_x ed il peso KN/m del profilato:

Adesso inizia la parte relativa allo SLE, poichè il foglio si calcola il q_e:
q_e = (1qs + 1qp + 0,5qa) x interasse = 26,46 KN/m
Imposto il Modulo elastico del c.a. pari a 8000 MPa ed ottengo una I_x:
I_x = (b*h^3)/12 = 210000cm⁴
Come risultato avrò un v_max = 0,552 cm, dato che mi conferma il progetto poichè I_x/ v_max >250

In questa seconda esercitazione analizzerò una struttura reticolare spaziale. Questo è un sistema costruttivo molto usato per realizzare coperture di luci importanti, poichè permette di realizzare grandi campate per mezzo di un numero limitato di supporti verticali, poichè la struttura trae forza dalla rigidità del telaio triangolare.

Utilizzo il software SAP 2000 per realizzare il modello su cui lavorare. I passaggi che bisogna seguire sono i seguenti:
1. Modellazione
2. Caratterizzazione: materiale e carichi
3. Analisi
4. Dimensionamento.

1. Modellazione
Come modulo base scelgo quello piramidale. Inizio con il disegnare quindi una piramide con il vertice verso il basso, inscritta all’interno di un cubo di lato l=1,5m. La griglia di riferimento usata è:
x= 5
y= 6
z= 2

2. Caratterizzazione: materiale e carichi
Per evitare di aver disegnato delle aste doppie seleziono tutti gli elementi e vado su Edit_Merge duplicate, in modo da unirli ed evitare anomalie nel corso delle analisi. Un ulteriore attenzione riguarda invece la tolleranza dei nodi; essendo la struttura costruita copiando un’unica base correggo la tolleranza. Seleziono tutta la struttura e vado su Edit_Edit points_Merge joints e confermo il valore pari a 0,1. Ultimo passaggio è quello di aggiungere i vincoli sui 4 appoggi (cerniere).

Dato che la struttura reticolare lavora a sforza normale di trazione o compressione, bisogna svincolare i nodi al momento. Seleziono quindi tutta la struttura e poi vado su Assign_Frame_Release/Partial Fixity e pongo il doppio flag al Moment (2-2) e Moment (3-3).

Procedo con la caratterizzazione di questo definendo un materiale (tubolare in acciaio) ed assegnando ai nodi superiori una forza F pari ad F=-80 KN. Seleziono quindi i nodi superiori e poi vado su Assign_Joints Load, scelgo la forza F che ho definito precedentemente ed imposto z=-80 KN

3. Analisi
Dopo aver impostato e caratterizzato la struttura faccio partire l’analisi lineare statica che ha come oggetto la forza F generata precedentemente.

Per conferma controllo la sollecitazione N,T,M. Quest’ultimi due non sono presenti, vista la caratterizzazione fatta prima, mentre il risultato dello sforzo assiale è qui riportato. Esporto tutti i dati relativi alla mia struttura su di un foglio di calcolo elettronico Excel per poter procedere con il dimensionamento delle aste.

4. Dimensionamento

Dopo aver ordinato il foglio Excel esportato, avrò per ogni singola asta il valore dello sforzo normale di trazione (+) o compressione (-).
Avendo un modulo piramidale devo considerarlo composto da aste di lunghezza diversa:
- Aste orizzontali = 1,5 m
- Aste diagonali = 2,12 m
- Aste inclinate = 1,67 m
Adesso ho tutti i ati per poter compilare i due fogli Excel.

4.1 Trazione  

Compilo il foglio riportando i valori di N di trazione (+) ottenuti precedentemente; aggiungo le caratteristiche dell'acciaio di carpenteria scelto (f_yk=235 MPa) ed il coefficiente γ_m=1,05. In questo modo per ogni singola asta ottengo una A_min (cm²⁾, risultato di A_min=(N*10)/f_yd. Procedo con il dimensionamento delle aste scegliendo i profili in base a questo valore ingegnerizzandolo.

4.2 Compressione

Per la compressione (+) la prima parte da compilare è identica alla precedente, ma devo considerare il fenomeno di instabilità, che non riguardava invece la trazione. Aggiungo quindi i valori di E=210000 MPa, beta=1, e la lunghezza dell'asta considerata. Ottengo così tre dati fondamentali per il dimensionamento:
-Lambda= pi*sqrt(E/f_cd)
-Rho_min= (l₀*100)/Lambda
-I_min= E*(Rho_min)².

Inizio il dimensionamento delle aste in base ai valori di Rho_min e I_min. Una verifica ulteriore di cui devo tenere conto è la Lambda finale che deve risultare <200.

 

Progetto di una trave in CEMENTO ARMATO,LEGNO ed ACCIAIO:

Una volta disegnata la mia carpenteria, prendo in considerazione la trave più sollecitata, ovvero quella centrale.

Prendendo in considerazione 1mq di solaio vado a calcolarmi tutti i carichi agenti sulla trave diversificandoli in carichi strutturali (qs) , carichi permanenti (qp) e carichi accidentali (qa). Per fare ciò io devo studiare e capire quanto volume ho in questo mq di ogni materiale e poi moltiplicare tale dato per il relativo peso specifico

Andiamo perciò a progettare una trave in CEMENTO ARMATO

 

Carichi strutturali : PIGNATTE,TRAVETTI, SOLETTA COLLABORANTE

PIGNATTE 9,1kg/mq x 8 = 0,73KN/mq  

SOLETTA COLLABORANTE CLS 24 KN/mc x ( 0,04m x 1m x 1m ) =0,96 KN/mq

TRAVETTI 24KN/mc x 2 (0,1m x 1m x 0,16m) =0,77 KN/mq 8 PIGNATTE 9 kg/mq x 8 = 0,77KN/mq

Carichi permanenti : PAVIMENTO GRANITO, MALTA D'ALLETTAMENTO,ISOLANTE ACUSTICO,MASSETTO,INTONACO

PAVIMENTO 27 KN/mc x ( 0.02 x 1m x 1m ) = 0,54 KN/mq

MALTA DI ALLETTAMENTO 770 1.400 Kg/mc x (0,03m x 1m x 1m ) = 0,42 KN/mq

ISOLANTE LANA DI VETRO 0,2 KN/mc x (0,06m x 1m x 1m ) = 0,012 KN/mq

MASSETTO ALLEGERITO 18KN/mc x (0,04m x 1m x 1m) = 0,72KN/mq

INTONACO 18KN/mc x (0,01m x 1m x 1m) = 0,18 KN/mq

IMPIANTI e TRAMEZZI 1,5 KN/mq (tale voce viene aggiunta per un'ulteriore sicurezza -

-dalla normativa)

 

Carichi accidentali : Ipotizzando un uso residenziale del mio progetto, il carico sarà di 2 KN/mq dato dalla normativa

qs = 2,46 KN/mq                                      qp = 3,37 KN/mq qa                                = 2 KN/mq

 

Adesso andando ad inserire tutti i carichi nella tabella EXEL si andrà a calcolare il carico ultimo (qu) cioè la somma di tutti i carichi moltiplicati per i propri coefficienti di sicurezza ed infine moltiplicati per l'interasse trovando intal modo il carico lineare distribuito sulla trave.

Lo scopo dei coefficienti di sicurezza è quello di aumentare il carico ultimo cosicchè la progettazione della trave risulti sovradimensionata e quindi più sicura.

 

qu = ( qs x 1,3 + qp x 1,5 + qa x 1,5 ) x 3 = 33.76 KN/m

 

Una volta trovato il mio carico qu che andrà a pesare sulla mia trave, posso trovare il Momento massimo che sarà pari a 151.92

 

FASE PROGETTUALE

 

Per il dimensionamento della mia trave scelgo

Acciaio S450 con Fyk = 450 Mpa

Cls di categoria "alte prestazioni" = C 55/67

 

Avendo scelto il materiale e quindi le forze caratteristiche è possibile ricavare la tensione di progetto sia dell'acciaio che del cemento armato.

Successivamente troviamo l'altezza utile e quindi l'altezza minima (per trovare l'altezza utile sarà necessario ricavare tramite le apposite formule i valori di “r” e di “beta”

 

Scegliendo arbitrariamente la base della nostra trave di 30 cm e un copriferro di 5cm, si ottiene un Hmin = 35,62 cm che consiste nel valore minimo dell'altezza della trave, lo vado ad ingegnerizzare cioè ad aumentare il suo valore.

Ipotizzo un altezza ultima della mia trave pari a H= 50cm

Il profilo della mia trave sarà di 30cm x 50cm ed è VERIFICATO

 

Andiamo a progettare una trave in LEGNO:

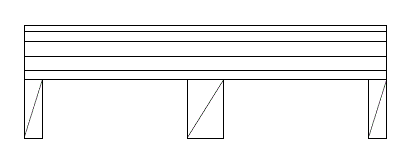
Carichi strutturali: TRAVETTI e TAVOLATO

TRAVETTI ( castagno) 10KN/mc x 2( 0,1m x 0,015 ) = 0,30 KN/mq

TAVOLATO( castagno) 6KN/mc x (0,025m x 1m x 1m) = 0.15 KN/mq

 

Carichi permanenti : PARQUET , MALTA ALLETTAMENTO, MASSETTO CEMENTIZIO

 

PARQUET(acero) 6KN/mc x (0,025m x 1m x 1m ) = 0,15 KN/mq

MALTA ALLETTAMENTO 18 KN/mc x ( 0,03m x 1m x 1m) = 0,54 KN/ mq

ISOLANTE (lana di legno) 0.18 KN/mc x (0.04m x 1m x 1m) = 0.0072

MASSETTO ALLEGERITO 18 KN/mc x (0,04m x 1m x1m ) = 0.72 KN/mq

IMPIANTI e TRAMEZZI +1,5 KN/mq

 

Carichi accidentali : Ipotizzando un uso residenziale del mio progetto, il carico sarà di 2 KN/mq dato dalla normativa

 

 

qs = 0,45 KN/mq qp = 2,92 KN/mq qa = 2 KN/mq

 

qu = ( qs x 1,3 + qp x 1,5 + qa x 1,5 ) x 3 = 23.9KN/mq

 

Una volta trovato il mio carico qu che andrà a pesare sulla mia trave, posso trovare il Momento massimo che sarà pari a 107,53 KNm .

 

FASE PROGETTUALE

Per il progetto del solaio scelgo un legno lamellare GL24h che ha una resistenza a flessione di fmk= 24Mpa

Ora vado ad impostare una possibile base della mia trave pari a 30cm che porterà tramite il calcolo un altezza minima della trave. Ingegnerizzando l'Hmin arriverò alla mia altezza ultima. H= 50cm

Il profilo della mia trave sarà di 30cmx50cm

 

FASE DI VERIFICA

Nella fase di verifica dovrò andare a considerare anche il peso proprio della trave appena progettata che andrò ad inserire nei carichi strutturali.

TRAVE: 10KN/mc x( 1m x 0,50m x 0,30m) = 1,5 KN/mq

 

il nuovo carico qu prevede una trave di Hmin= 45.32cm quindi il mio profilo è VERIFICATO in quanto avevo considerato un altezza H pari a 50cm.

 

 

 

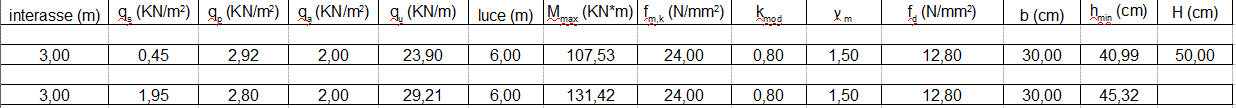
Andiamo a progettare una trave in ACCIAIO

 

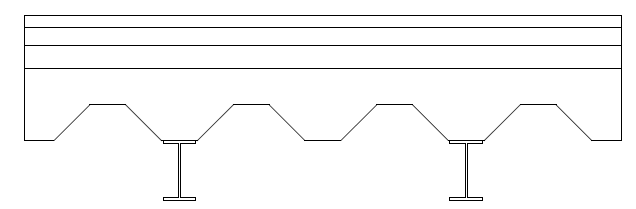
Carichi strutturali:TRAVETTO,MASSETTO e LAMIERA GRECATA

TRAVETTO(IPE100) 78,5KN/mc x (0,001 mq x 1m) = 0.078

LAMIERA GRECATA spessore della lamiera 5mm = 0,4 KN/mq (tabellato dalla casa produttrice)

MASSETTO ALLEGERITO 24KN/mc x (0,09m x 1m x 1m) = 2.16 KN/mq

Carichi permanenti: PAVIMENTO , MALTA ALLETTAMENTO, ISOLANTE

PAVIMENTO (granito) 30KN/mq x (0.02 x 1m x 1m) = 0,6 KN/mq

MALTA ALLETTAMENTO 18KN/mq x (0,03m x 1m x 1m) = 0,54 KN/mq

ISOLANTE (lana di roccia) 90kg/mc x (0,04m x 1m x 1m) = 0,36KN/mq

IMPIANTI e TRAMEZZI +1,5 KN/mq

 

 

Carichi accidentali: Ipotizzando un uso residenziale del mio progetto, il carico sarà di 2 KN/mq dato dalla normativa

 

qs = 2,64 KN/mq qp = 3 KN/mq qa = 2 KN/mq

 

qu = ( qs x 1,3 + qp x 1,5 + qa x 1,5 ) x 3 = 30,69 KN/mq

 

Una volta trovato il mio carico qu che andrà a pesare sulla mia trave, posso trovare il Momento massimo che sarà pari a 138,11 KNm .

 

FASE PROGETTUALE

Scelgo l'acciaio Fe 430/S275 che avrà una tensione di snervamento pari a 275Mpa e otterrò un modulo di resistenza Wxmin pari a 563,49 cmc che equivale ad un IPE 300 perchè considero un Wx pari a 628.36 cmc.

 

FASE DI VERIFICA

Nella fase di verifica dovrò andare a considerare anche il peso proprio della trave appena progettata che andrò ad inserire nei carichi strutturali.

Peso trave IPE 300 = 0,005381 mc x 78 KN/mc = 0,42 KN/m

 

Andando a considerare anche il peso della trave progettata, il Wxmin equivale a 591.64 cmc, e non superando il valore preso di Wx scelto posso dire che la sezione è VERIFICATA