SdC(b) (LM PA)

questi sono i temi proposti nell'esonero

ciao!

Dato il solaio di carpenteria sopra raffigurato, eseguo il progetto della trave centrale maggiormente sollecitata di luce pari a 5 m con un impalcato in acciaio, uno in latero cemento e uno in legno. Il retino evidenziato rappresenta l'area d'influenza incidente sulla trave centrale (Area d'influenza=luce*interasse). Il dimensionamento tramite le tre tecnologie avviene considerando  1mc di solaio.

SOLAIO IN ACCIAIO:

I PASSAGGIO:

Calcolo il contributo del carico strutturale moltiplicando il volume dell'elemento per il suo peso specifico su un mq di solaio. Il peso specifico non è altro che il rapporto tra il peso di un campione di materiale e il suo volume.

Carico strutturale: getto di cls+lamiera grecata+travi secondarie IPE 160

Getto di cls: (0,06 * 1)[mc/mq] * 25[KN/mc] = 1,5[KN/mq]

Lamiera grecata: 7,85[Kg/mq]/100 = 0,078[KN/mq]

Travi secondarie IPE160: 2*(0,0020 * 1)[mc/mq] * 78,5[KN/mc] = 0,314[KN/mq]

II PASSAGGIO:

Calcolo il contributo del carico permanente non strutturale facendo le stesse operazioni applicate per il carico strutturale.

Carico permanente non strutturale: pavimento in gres porcellanato+massetto di livellamento+controsoffitto in cartongesso+1,5[KN/mq] (ovvero la somma degli impianti 0,5[KN/mq] e dei tramezzi 1[KN/mq])

Pavimento in gres porcellanato: (0,02 * 1 * 1)[mc/mq] * 20[KN/mc] = 0,4[KN/mq]

Massetto di livellamento: (0,04 * 1 * 1)[mc/mq] * 21[KN/mc] = 0,84[KN/mq]

Controsoffitto in cartongesso: (0,015 * 1 * 1)[mc/mq] * 13,25[KN/mc] = 0,2[KN/mq]

Considero inoltre il carico accidentale (carico variabile nel tempo) pari a 2[KN/mq]

III PASSAGGIO:

Trovo il carico strutturale totale: qs = 1,5+0,314+0,078 = 1,9[KN/mq]

Trovo il carico permanente non strutturale totale: qp = 0,4+0,84+0,2+1,5 = 2,94[KN/mq]

qa = 2[KN/mq]

IV PASSAGGIO:

Effettuo la combinazione fondamentale allo SLU, moltiplicando il totale dei carichi strutturali, permanenti non strutturali e variabili per dei coefficienti parziali di sicurezza considerati nella condizione più sfavorevole. Il coefficiente relativo a qs è 1,3, quello relativo a qp è 1,5 e quello relativo a qa è 1,5.

qtot  = (1,9*1,3)[KN/mq] + (2,94*1,5)[KN/mq] + (2*1,5)[KN/mq] = 9,88[KN/mq]

Poichè questo carico totale fa riferimento a quello distribuito su 1mq di solaio, per trovare il carico lineare agente sulla trave, devo calcolare il contributo del carico relativo all'area d'influenza incidente sulla trave sollecitata (qtot*A) e il risultato che ottengo lo divido per la luce della trave sollecitata.

A = L*i = 5[m]*4,75[m] = 23,5 mq

q(area d'influenza) = qtot*A = 9,88[KN/mq]*23,75[mq] = 234,65[KN]

qu(lineare) = (qtot*A)/L = 234,65[KN]/5[m] = 46,93[KN/m]

Questo risultato lo posso riscontrare nella tabella del file Excel, che mi effettua il calcolo automaticamente

V PASSAGGIO:

Sapendo che il Momento massimo di una trave doppiamente appoggiata di luce L è ql^2/8, calcolo il momento massimo della trave in esame = (qu(lineare)*L^2)/8 = =46,93[KN/m]*25[mq])/8 = 146,66[KN*m]

Ora scelgo acciaio S275 con fyk=275[N/mmq] = 27,5[KN/cmq] e fyd=27,5[KN/cmq]/1,05=26,19[KN/cmq] e mi trovo la resistenza minima di progetto  Wxmin=Mmax/fyd = 14666[KN/cm]/26,19 = 559,98[KN/cm]

Vado sul sagomario e scelgo un IPE con Wx >/= 559,98[KN/cm]

IPE 330 -> Wx=713 cmc

Questi calcoli sono confermati dal foglio Excel

VI PASSAGGIO:

Aggiungo il peso della trave scelta al calcolo dei carichi strutturali, sapendo che il peso dell'IPE330 è di 49,1 [Kg/m]=0,49[KN/m]

qu= 9,88[KN/mq]*4,75[m] + 0,49[KN/m]*1,3 = 47,6[KN/m]

Ricalcolo Mmax=(47,6[KN/m]*25[m])/8= 148,6[KN*m]

Wxmin=14866[KN*cm]/26,19[KN/cmq]= 567,54[cmc] che è < 713 cmc

Quindi la scelta IPE330 è esatta e cambiando il dato qu nel foglio excel confermo la mia ipotesi

SOLAIO IN LATERO CEMENTO:

Nel progetto della trave in acciaio ho spiegato gradualmente i vari passaggi. Adesso li applico nuovamente andando più velocemente.

Carico strutturale: soletta collaborante+pignatte+travetti

Soletta collaborante: (0,04*1*1)[mc/mq] * 25[KN/mc] = 1[KN/mq]

Pignatte: 8*(7[kg/mq])=56[Kg/mq]= 0,56[KN/mq]

Travetti: 2*(0,12*0,12*1)[mc/mq] * 25[KN/mc]= 0,72[KN/mq]

Carico permanente non strutturale: pavimento in gres porcellanato+massetto di livellamento+intonaco

Pavimento in gres porcellanato: (0,02*1*1)[mc/mq] * 20[KN/mc] = 0,4[KN/mq]

Massetto di livellamento: (0,04*1*1)[mc/mq] * 21[KN/mc]= 0,84[KN/mq]

Intonaco: (0,02*1*1)[mc/mq] * 20[KN/mc]= 0,4[KN/mq]

Carico accidentale variabile

2[KN/mq]

Carico strutturale totale:

qs= 1+0,56+0,72=2,28[KN/mq]

Carico permanente non strutturale totale (con l'aggiunta di 1,5[KN/mq]):

qp= 0,4+0,84+0,4+1,5= 3,14[KN/mq]

Il carico totale qtot=qs*1,3+qp*1,5*qa*1,5=[50,7KN/mq]

Come possiamo notare, rispetto alla tabella dell'acciaio, come compaiano altri valori: questo è dettato dalla disomogeneità del materiale, poichè possiamo calcolare i due materiali (il cls compresso) e l'acciaio (teso) come due materiali con comportamento meccanico diverso tra loro. Per cui compaiono fyd che è la tensione allo snervamento dell'acciaio e fck che è la resistenza a compressione del calcestruzzo. Il tutto è intimamente legato, poichè come notiamo entrambe le resistenze occorrono per determinare l'altezza di progetto utile e totale di progetto. Ovviamente c'è un'ingenierizzazione finale che consiste nell'approssimare per eccesso l'altezza della trave per comodità costruttiva.

Sezione trave principale

SOLAIO IN LEGNO:

Carico strutturale: tavolato+travetti

Travetti: 2*(0,08*0,1*1)[mc/mq] * 4[KN/mc] = 0,064[KN/mq]

Tavolato: (0,03*1*1)[mc/mq] * 6[KN/mc]= 0,18[KN/mq]

Carico permanente non strutturale: pavimento in gres porcellanato+massetto cls+allettamento+controsoffitto in cartongesso

Pavimento in gres porcellanato: (0,02*1*1)[mc/mq] * 20[KN/mc]=0,4[KN/mq]

Massetto in cls: (0,04*1*1)[mc/mq] * 14[KN/mc]= 0,56[KN/mq]

Allettamento: (0,02*1*1)[mc/mq] * 20[KN/mc]= 0,4[KN/mq]

Controsoffitto in cartongesso: (0,015*1*1)[mc/mq] * 13,25[KN/mc]= 0,2[KN/mq]

Carico accidentale variabile

2[KN/mq]

Carico strutturale totale:

qs= 0,064+0,18=0,24[KN/mq]

Carico permanente non strutturale totale (con l'aggiunta di 1,5[KN/mq]):

qp= 0,4+0,56+0,4+0,2+1,5= 3,06[KN/mq]

Il carico totale qtot=qs*1,3+qp*1,5*qa*1,5=[37,53KN/mq]

Per verificare se l'altezza ipotizzata, anche aggiungendo il peso proprio della trave risulti verificata, ho aggiunto ai carichi totali il peso proprio della trave moltiplicandolo per 1,3 (coeff. carichi strutturali) e la sezione risulta ugualmente verificata.

Sezione trave principale

Dimensionamento di massima di Travi in Legno, Acciaio, Calcestruzzo Armato

Dal “DECRETO MINISTERIALE – NORME TECNICHE PER LE COSTRUZIONI”del 2008:

“Le opere e le componenti strutturali devono essere progettate, eseguite, collaudate e soggette a manutenzione in modo tale da consentirne la prevista utilizzazione in forma economicamente sostenibile e con il livello di sicurezza previsto dalle presenti norme.

La sicurezza e le prestazioni di un’opera o di una parte di esse devono essere valutate in relazione agli stati limite che si possono verificare durante la vita nominale. Stato limite è la condizione superata la quale l’opera non soddisfa più le esigente per le quali è stata progettata.”

STATI LIMITE ULTIMI (SLU): valutazione della sicurezza al fine di evitare crolli, perdite di equilibri e dissesti di varia entità, che possano portare a perdita di bene e mettere in pericolo persone, ambiente. In definitiva l’opera risulterebbe FUORI SERVIZIO; con il superamento dello SLU di crea situazione di COLLASSO IRREVERSIBILE.

STATI LIMITE DI ESERCIZIO (SLE): analisi e calcoli atti a garantire le prestazioni di esercizio. Con il superamento di uno SLE si può avere carattere REVERSIBILE o IRREVERSIBILE.

Nessuno STATO LIMITE è superato quando si usano nei modelli valori opportuni di azioni, proprietà dei materiali e dati geometrici.

Vanno quindi definiti i materiali, le tecnologie e le caratteristiche fisico-meccaniche delle strutture affinchè sia garantita la durabilità della stessa, e i termini limite ai fini della sicurezza.

Le opere vanno verificate:

-per gli stati limite ultimi in combinazione con le azioni di progetto;

-per gli stati limite di esercizio in base alle prestazioni attese.

I materiali a loro volta vanno scelti in seguito a verifiche fisico-meccaniche di laboratorio al fine di una idonea qualificazione e valutazione dei limiti di sicurezza.

Per il dimensionamento di massima di una trave di un solaio adotteremo un metodo progettuale per il quale valuteremo che la tensione massima della trave maggiormente sollecitata sia uguale alla tensione di progetto del materiale. La struttura verrà schematizzata come la somma di telai piani con travi collaboranti ai pilastri (considerati come appoggi semplici).

A livello progettuale come già riportato potremmo:

-VERIFICARE LA RESISTENZA STRUTTURALE: data quindi una struttura di cui si conosce geometria e materiale, definiti i suoi carichi, si verifica che la struttura sopporti i carichi;

-PROGETTARE A RESISTENZA: assegnata una funzione, si impone che la struttura resista e sulla base della resistenza di scelgono geometria e materiale.

Quindi, definita la pianta di carpenteria, determiniamo all’interno del telaio quale sia la trave maggiormente sollecitata e su essa dimensioniamo le altre.

Con l’aiuto del foglio di calcolo andiamo a definire quali sono i carichi agenti sulla trave e in base alla lunghezza della stessa andremo a calcolarci il momento massimo in mezzeria, la sigma massima e quindi l’altezza della trave (da ricordare che sono le ascisse a definire sigma maggiore tanto più ci si allontana dal centro dell’area).

In questa esercitazione non vengono calcolate le travi secondarie poiché esse sono solo di collegamento tra le principali onde evitare che esse “scorrano”.

Nella nostra esercitazione (SLU) andremo a utilizzare la COMBINAZIONE FONDAMENTALE:

    Υg1⋅G1 + Υg2⋅G2 + Υp⋅P + Υq1⋅Qk1 + Υq2⋅Ψ02 ⋅ Qk2 + Υq3⋅Ψ03 ⋅ Qk3…

I valori dei coefficienti di combinazione sono dati dalla TAB. 2.5.I             

I valori dei coefficienti parziali di sicurezza γGi d γQj sono dati dalla TAB 2.6.I e vengono forniti da assumere per la determinazione degli effetti delle azioni nelle verifiche agli stati limite ultimi;

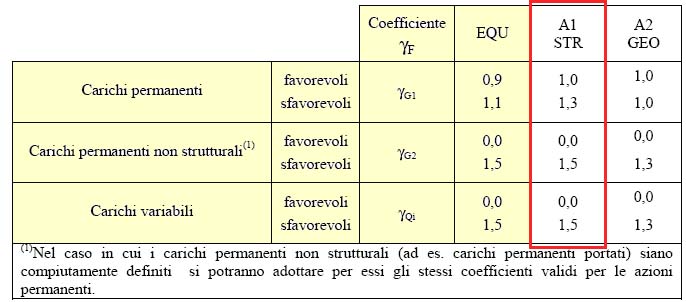
dove   γG1= coeff. Parziale del peso proprio della struttura;

           γG2= coeff. Parziale dei pesi propri degli elementi non strutturali;

            γQi = coeff. Parziale delle azioni variabili.

Definiamo allora la nostra pianta del solaio.

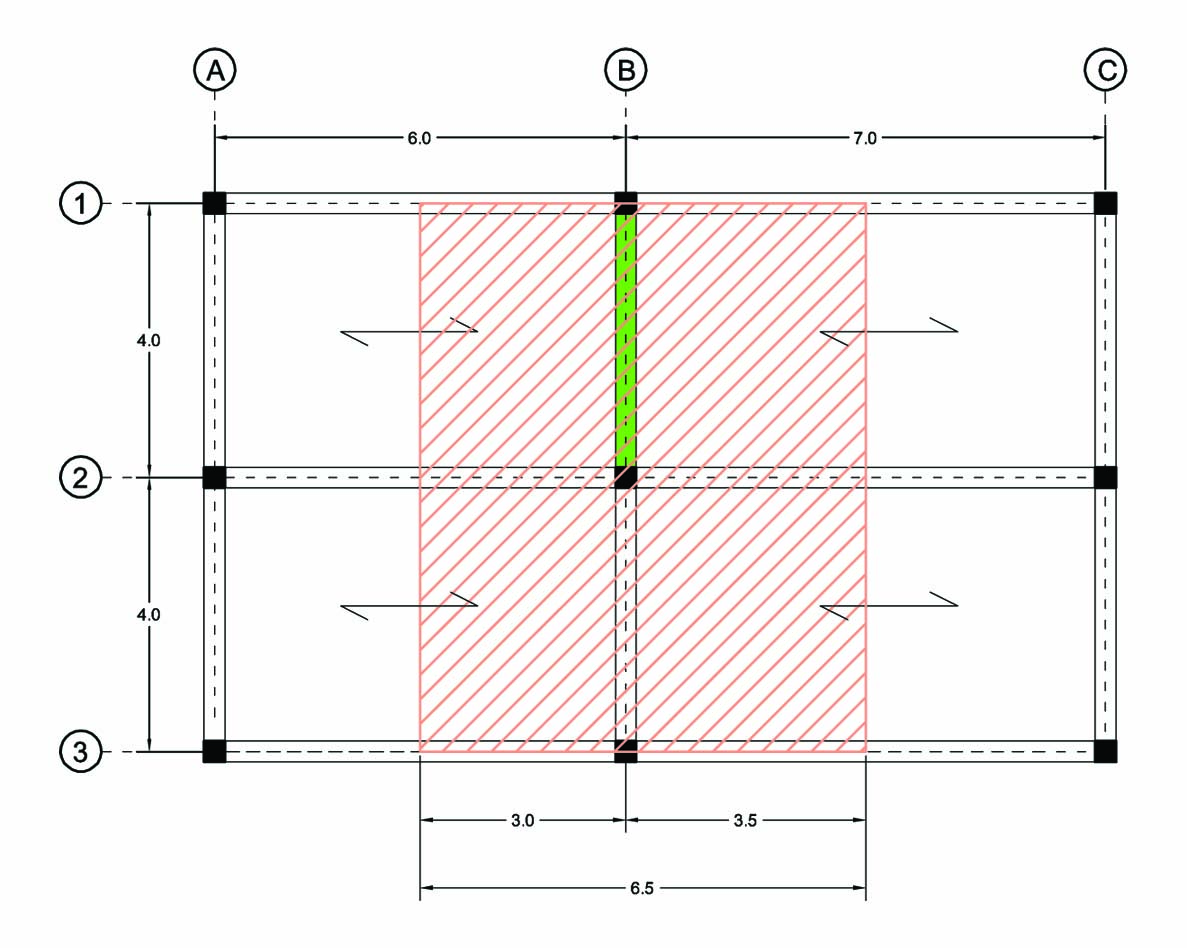Quella che vediamo segnata in rosso è l'area di influenza di cui si fa carico la trave, in verde ho invece evidenziato la trave maggiormente sollecitata.

Vado ora ad analizzare ognuna delle tre tecnologie adottate per il solaio, cominciando da quella in acciaio:

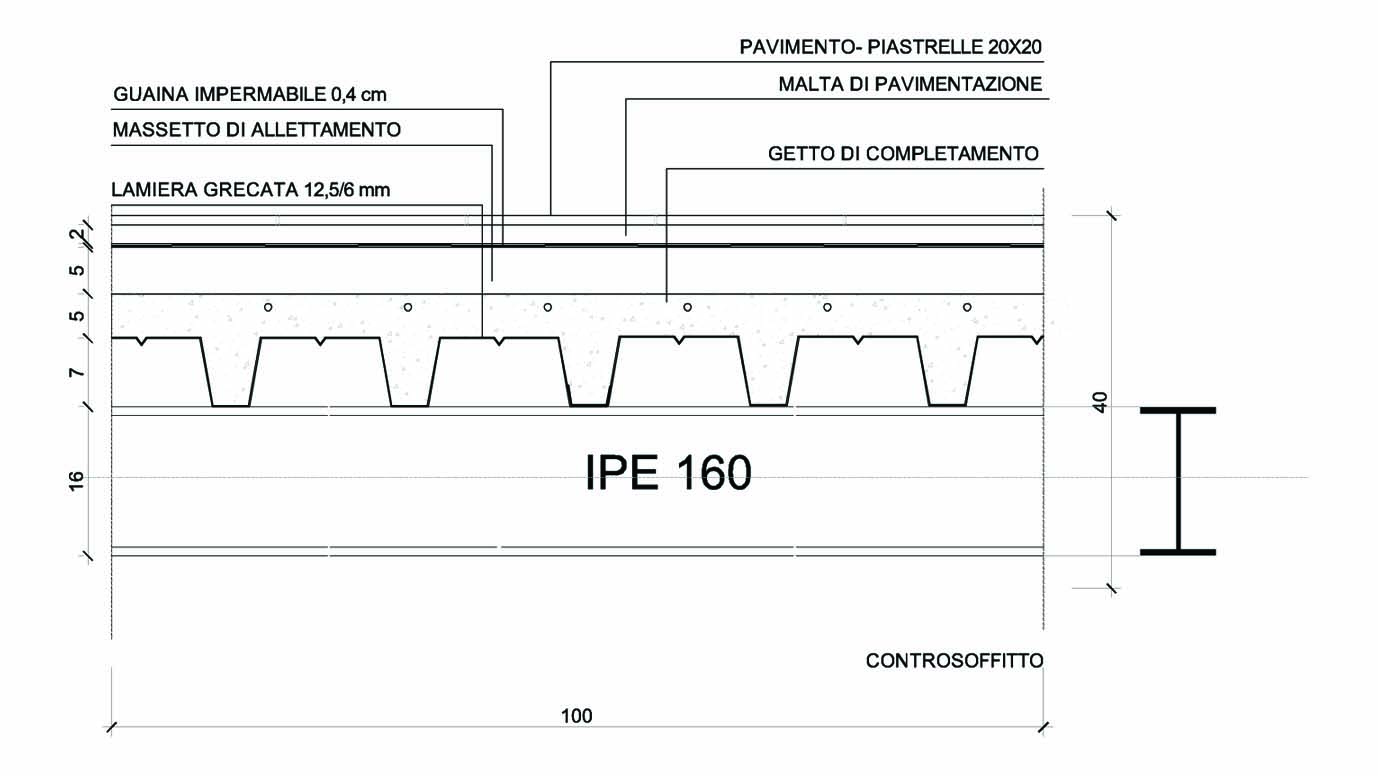
Andando così a definire il carico derivante da ogni strato, per geometria e peso specifico in una porzione di 1 metro cubo di solaio:

Acciaio:

CARICHI STRUTTURALI Qs:

TRAVE IPE 160: una ogni 0,5 m, sezione trave 0,0020 m^2         peso specifico materiale 78,5 kN/m^2

LAMIERA GRECATA: che copre 1 m x 1 m                                  peso specifico: 0,078 kN/m^2

GETTO DI RIEMPIMENTO: (area 0,645 m^2 x 1 )                       peso specifico: 25 kN/m^2

CARICHI PERMANENTI Qp:

PAVIMENTAZIONE IN KLINKER: misure (0,2 m x 0,2 m x 0,01 m)  peso specifico 21 kN/m^2

MALTA DI PAVIMENTAZIONE: misure (1m x 1m x 0,02 m)              peso specifico 20 kN/ m^2

GUAINA IMPERMEABILE: misure (1m x 1m x 0,004m )                     peso specifico 0,02 kN/m^2

MASSETTO: misure (1m x 1m x 0,05 m)                                                  peso specifico 14 kN/m^2

CONTROSOFFITTO CARTONGESSO:  misure (1m x 1m x 0,015 m) peso specifico 13,25 kN/m^2

Cui vanno aggiunti CARICHI TRAMEZZI : 1kN/m^2 e CARICHI IMPIANTI : 0,5 kN/m^2

CARICHI ACCIDENTALI Qa per ambienti a uso residenziale: 2kN/m^2

da cui: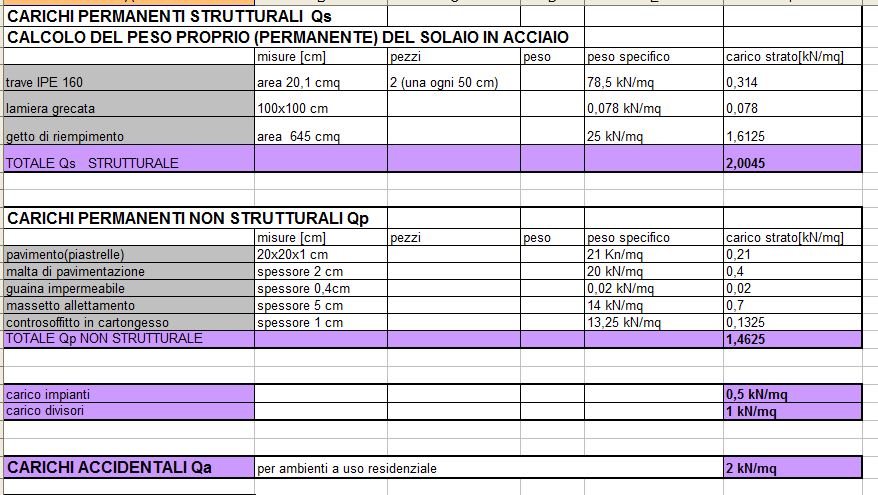  

CARICHI STRUTTURALI: li ho calcolati e sono i carichi derivanti dal peso degli elementi strutturali secondari come i travetti di un solaio

SOVRACCARICHI PERMANENTI: sempre da calcolare sulla base geometrico-fisico degli strati e sono quei carichi che gravano permanentemente sulla struttura, ma non costituiscono struttura

CARICHI ACCIDENTALI: dati da normativa (NTC2008- Norme tecniche per le costruzioni- D. M. 14 Gennaio 2008), si riferiscono a quei carichi che gravano in maniera non permanente, ma che comunque hanno una alta probabilità di incidere sul carico complessivo. Nel nostro caso sono dati come 2 kN/mq per ambienti a uso residenziale.

[giusto per stare più sicuri possiamo pensare all'ordine di grandezza dei carichi strutturali che ne caso di un solaio in latero-cemento sono di circa 2,5 kN/m^2, nei solai in legno di circa 0,5 kN/m^2 e nei solai in acciaio si aggirano su 1,5 kN/m^2]

Ottenuti ora i carichi di cui si fa carico la mia trave, ipotizzata come travatura secondaria una composta da travetti ipe 160  la cui sezione e il peso sono forniti da normativa, procedo inserendo i dati trovati in un altro foglio excel che mi fornirà il Momento massimo sulla trave derivante dal carico linearmente distribuito. Mi avvalgo inoltre del foglio excel per definire i miei valori di resistenza fyk e fyd e calcolare quindi la Wx ossia la resistenza di progetto che mi indirizza verso la scelta del profilo IPE a me necessario.

che mi porta a scegliere nel mio caso 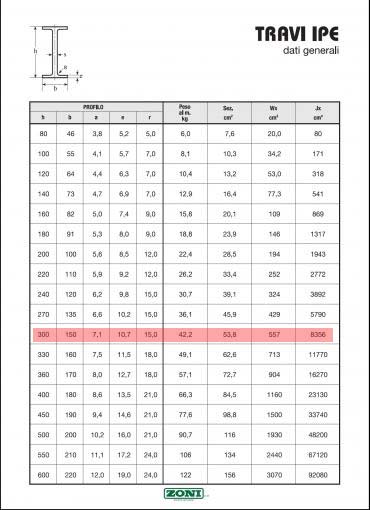 ossia una trave IPE 300.

Ricapitolando:

Come abbiamo capito il carico  totale Qtot deriva da: (qs*1,3)+ (qp*1,5)+ (qa*1,5).

Riporto il calcolo della tecnologia da me scelta in acciaio:

Qtot= (2,00 kN/m^2 * 1,3) + (2,96 kN/m^2*1,5) + (2,00 kN/m^2*1,5)= 10,04 kN/m^2 ossia il CARICO UNIFORMEMENTE DISTRIBUITO SU UN METRO QUADRO DI SOLAIO.

Poiché devo ricondurre il modello fino ad avere un carico LINEARE agente sulla trave maggiormente sollecitata per cui devo:

1. q tot x A influenza trave = carico distribuito sulla superficie del solaio che influenza trave

 A= l x i      A= 6,5 m x 4 m = 26 mq      da cui poi    10,04 kN/m^2 x 26 m^2= 261,04 kN

2.per trovarmi ora il carico lineare sulla trave come qu= 261,04 kN/ 4 m = 65,26 kN/m  

         perchè           (qu= q tot/l)

Passo ora a calcolarmi il Mmax sulla trave che calcolo come una trave doppiamente appoggiata:

Mmax=[qu x( l^2)]/8   nel mio caso in esame: (65,26 kN/m x 16)/8=  130,52 kN*m

Abbiamo scelto S275 con cui       fyk=27,5kN/cmq          e          fyd= 27,5/1,05= 26,19 kN/cmq

Wxi min= M max/ fyd= 130,52 kN*m/ 26,19 kN/cmq= 498,35 cm^3

Ora scelgo una IPE 300

E devo aggiungere il peso della trave ai carichi strutturali qs. Sapendo che 1m trave IPE 300 ha peso specifico è 42,2 kg/m= 0,42 kN/m lo aggiungo a qu= 10,04x 6,5+ (0,42 x 1,3)= 65,80 nK*m

M max= [(65,80 x 16) kN/m^2]/8= 131,61 kN*m

Wxi max=131,61/26,19= 503 cm^3 < 557 cm^3

                                             TRAVE VERIFICATA!

Vado ora ad analizzare gli altri due solai con differenti tecnologie:

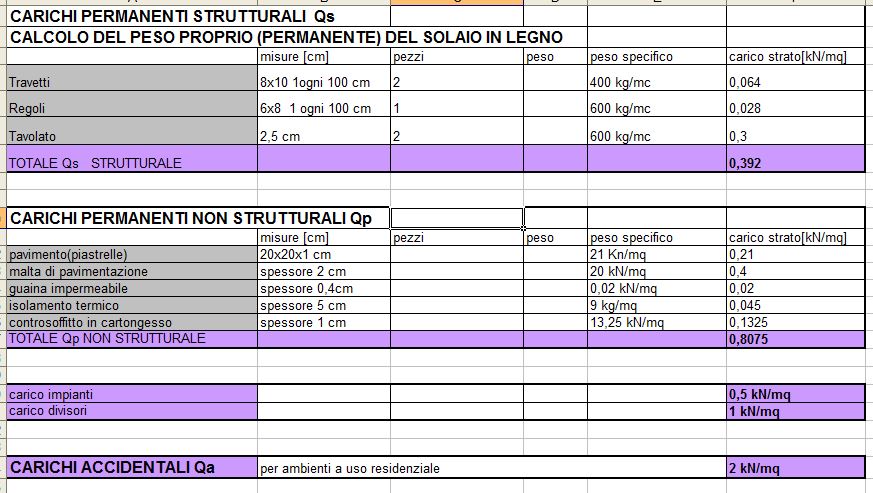
Legno:

CARICHI STRUTTURALI Qs:

TAVOLATO: misure (1m x 1m x 0,025m) x2         peso specifico 6kN/m^3 

TRAVETTI:  misure (0,08m x 0,1m x 1m) x2         peso specifico 4 kN/m^3

REGOLI:  misure (0,06m x 0,08m x 1m)                 peso specifico 6 kN/m^3                 

CARICHI PERMAMENTI Qp:

PAVIMENTAZIONE IN KLINKER: misure (0,2 m x 0,2 m x 0,01 m)  peso specifico 21 kN/m^2

MALTA DI PAVIMENTAZIONE: misure (1m x 1m x 0,02 m)     peso specifico 20 kN/ m^2

GUAINA IMPERMEABILE: misure (1m x 1m x 0,004m )           peso specifico 0,02 kN/m^2

ISOLAMENTO TERMICO: misure (1m x 1m x 0,05 m)               peso specifico 0,09 kN/m^2

CONTROSOFFITTO CARTONGESSO:  misure (1m x 1m x 0,01 m) peso specifico 13,25 kN/m^2

Cui vanno aggiunti CARICHI TRAMEZZI : 1kN/m^2 e CARICHI IMPIANTI : 0,5 kN/m^2

CARICHI ACCIDENTALI Qa per ambienti a uso residenziale: 2kN/m^2

IMPORTANTE: prima ho dimenticato di dire che spesso i pesi specifici vengono forniti talvolta in kN/m^2,  o come kg/m^2 o a volte come nel caso delle pignatte come kg al pezzo. Mi è capitato anche un g/cm^3. A quel punto si tratta di portare particolare attenzione nelle equivalenze al fine di avere dati quanto più omogenei nelle unità di misura. Ricorderemo ad es che 1KN=100 Kg  che risulterà più comoda come unità di misura quando andiamo a calcolare i carichi superficiali (anche densità di carico).

Quindi, riprendo l'analisi dei calcoli per il solaio in legno:

Mi avvalgo nuovamente del foglio excel:

da cui per quanto già spiegato prima  sommo ai qs il peso proprio della mia trave:

(0,40 m x 0,35m x 1m)* 7 kN/m^3= 0.98 kN/m^2  che andrà moltiplicato sempre per 1.3 che è il coefficiente parziale di sicurezza per carichi strutturali e ne deriva

 che verifica le dimensioni della trave principale che ho progettato: 

                                    ANCHE QUESTA è VERIFICATA! (con mia grande gioia!)

Passiamo ora al solaio in LATERO CEMENTO:

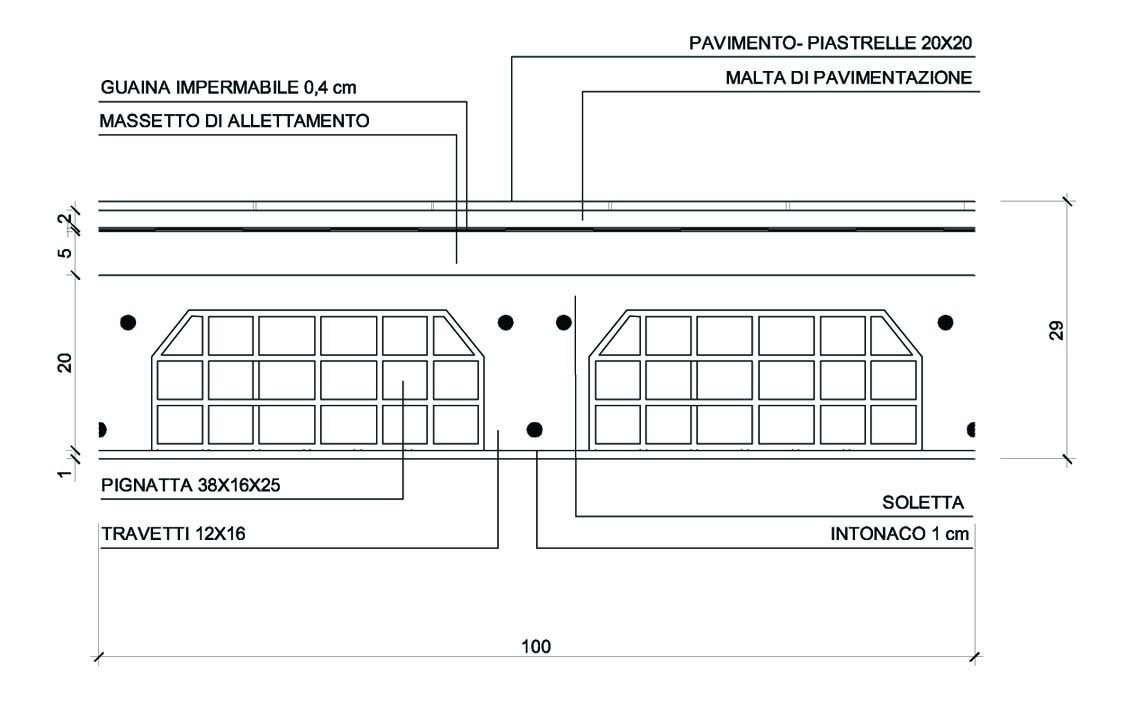
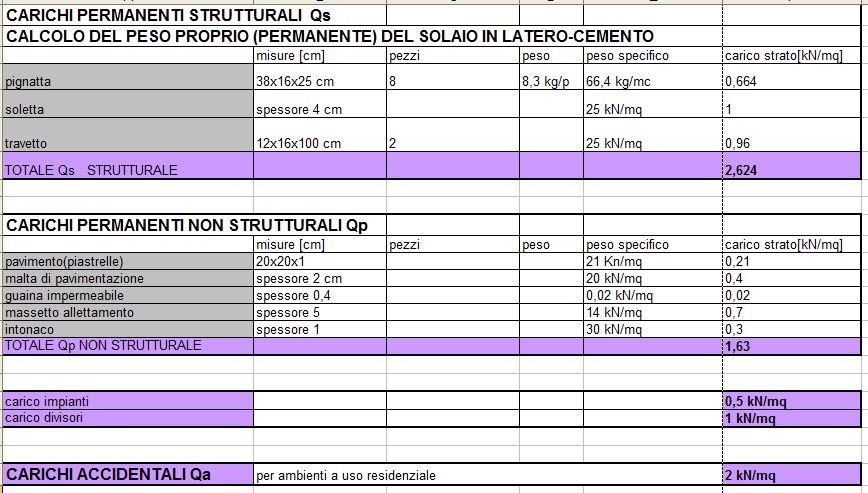
Latero-cemento:

CARICHI STRUTTURALI Qs:

PIGNATTA IN LATERIZIO: misure (0,38m x 0,16m x 0,25m)    peso specifico 8,3 kg/pezzo. Nel mio caso 8 pz

SOLETTA: misure (1m x 1m x 0,04 m)                                     peso specifico 25 kN/m^2

TRAVETTI: misure (0,12 m x 0,16m x 1m) x 2 pezzi                 peso specifico 25 kN/m^2

CARICHI PERMANENTI Qp:

PAVIMENTAZIONE IN KLINKER: misure (0,2 m x 0,2 m x 0,01 m)  peso specifico 21 kN/m^2

MALTA DI PAVIMENTAZIONE: misure (1m x 1m x 0,02 m)       peso specifico 20 kN/ m^2

GUAINA IMPERMEABILE: misure (1m x 1m x 0,004m )        peso specifico 0,02 kN/m^2

MASSETTO: misure (1m x 1m x 0,05 m)                           peso specifico 14 kN/m^2

INTONACO:  misure (1m x 1m x 0,01 m)                         peso specifico 30 kN/m^2

Cui vanno aggiunti CARICHI TRAMEZZI : 1kN/m^2 e CARICHI IMPIANTI : 0,5 kN/m^2

CARICHI ACCIDENTALI Qa per ambienti a uso residenziale: 2kN/m^2

Vado ora a intabellarli per trovare M max della una trave doppiamente appoggiata di luce l.

Seppure il latero cemento è considerato molto performante, seppure la posa in opera a getto creano situazioni di possibile carico variante e la disomogeneità dei materiali che compongono il materiale rendono il calcolo più complesso.

Per il calcolo dei carichi strutturali andrò ad esempio a conteggiare il numero di pignatte e di travetti presenti in un metro cubo di solaio. Per il carico strutturale calcolo il volume su un metro lineare di ciascun travetto e lo moltiplico per il peso specifico del calcestruzzo armato (25 kN/m^2) e moltiplico ancora tutto per il numero dei travetti in un metro quadrato di solaio.

Nel completare il foglio excel con i carichi permanenti, strutturali e accidentali, l’area di interasse e la luce, devo tener conto anche di fy (tensione allo snervamento dell’acciaio) per l’armatura, della fck ossia la resistenza caratteristica del cls fino a determinare l’altezza utile (da inizio sezione in alto a copri ferro). Quindi per ottenere l’altezza totale devo sommare i centimetri del  ‘copriferro’ e vado a ricavarmi l’altezza totale della mia trave principale. Con particolare attenzione poiché in questo caso (più che negli altri due) il peso proprio della trave è sensibilmente importante e “pesante”.

da cui ho:    

però vorrei precisare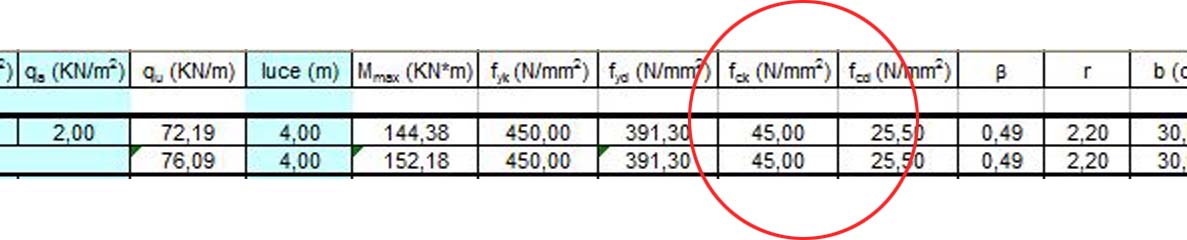 

che ho ritenuto di adottare un calcestruzzo con resistenza a compressione fck (o 0,83* Rck a seconda della forma del provino) di classe C35/45 che rientra nel calcestruzzo ordinario (NSC - Normal Strenght Concrete) non avendo nel mio caso luce esagerata e/o funzioni particolari.

   STRUTTURA IN CEMENTO ARMATO

   Innanzitutto disegniamo la carpenteria, andando ad individuare la trave più sollecitata:

La zona tratteggiata in rosso è l’area di pertinenza della trave che abbiamo individuato, con un valore di interasse pari a 5 metri.
Apriamo adesso il nostro file Excel e selezioniamo il foglio destinato al dimensionamento delle strutture in cemento armato.
Il foglio è strutturato in modo che le celle in cui vanno inseriti i dati siano azzurrine, mentre quelle di calcolo automatico bianche. 

Il primo dato da inserire è proprio l’interasse.

Successivamente ci vengono richiesti i carichi agenti sul solaio:

q_s: carico strutturale, ovvero il carico dovuto al peso proprio della parte strutturale del solaio;

q_p: carico permanente, ovvero il carico dovuto agli ulteriori strati componenti il solaio che non hanno funzione strutturale, ai tramezzi, agli impianti, a tutto ciò in sostanza che grava in modo permanente sulla parte strutturale;

q_a: carico accidentale, sono regolati dalla normativa, e possono comprendere i carichi di esercizio, il sisma etc.

Per l’analisi dei carichi prendiamo in considerazione un metro quadro di solaio, di cui nell’immagine di sopra riportiamo la sezione con gli spessori dei vari strati.

Per calcolare il peso su un metro quadro di ogni materiale, dobbiamo conoscere il suo peso specifico, solitamente espresso in KN/m³, e moltiplicarlo per il suo volume contenuto in un metro quadro (m³/m²).
 

Iniziamo con il carico strutturale: nel caso del cemento armato, la funzione strutturale è svolta dalla soletta in cls, dalle pignatte, e dai travetti.
I pesi specifici che adesso  ci servono sono dunque:

Calcestruzzo: 24 KN/m³
Pignatta 16x40x25: 8 kg/cad

Calcoliamo [volume/m² x peso specifico]:

q_s Soletta: (0.04m x 1m x 1m)/m² x 24 KN/m³ = 0.96 KN/m²

q_s Pignatte: 2 x 4 x 8 kg/m² = 64 kg/m² x 10^-2= 0.64 KN/m²

q_s Travetti: (0.16m x 0.2m x 1m)/m² x 24 KN/m³ = 0.768 KN/m²

q_s Tot= 0.96 KN/m² + 0. 64 KN/m² + 0.768 KN/m²= 2.368 KN/m²

Andiamo dunque ad inserire il dato ottenuto nella tabella Excel, sotto il valore q_s.

Calcoliamo ora i carichi permanenti. In questa categoria, come già detto, ricadono tutti i pesi fissi agenti sulla parte strutturale, come gli intonaci, le mattonelle, i massetti di livellamento, gli impianti e i tramezzi divisori interni. Di questi ultimi due in particolare non andremo a fare un calcolo esatto, ma aggiungeremo al totale raggiunto 1kN/m² per i tramezzi e  0,5 kN/m² per gli impianti, poiché sono dati difficili da calcolare e , come nel caso dei tramezzi, possono mutare nel tempo.

Per i carichi permanenti, i pesi specifici di cui necessitiamo sono:

Mattonelle in ceramica: 31,250 KN/m³
Massetto: 2000 Kg/m³= 2000 x 10^-2 KN/m³ = 20 KN/m³
Isolante: 30 Kg/m³ = 30 x 10^-2 KN/m³ = 0.3 KN/m³
Intonaco: 18 KN/m²
 

Calcoliamo:

q_p Pavimento: (0.02m x 1m x 1m)/m² x 31.250 KN/m³ = 0.625 KN/m²

q_p Massetto: (0.03m x 1m x 1m)/m² x 20 KN/m³ = 0.6KN/m²

q_p Isolante: (0.06m x 1m x 1m)/m² x 0.3 KN/m³ = 0.018 KN/m²

q_p Intonaco: (0.01m x 1m x 1m)/m² x 18 KN/m³ = 0.18 KN/m²

q_p Tot= 0.625 KN/m² + 0.6KN/m²+ 0.018 KN/m² = 1.423 KN/m²  (+ 1 KN/m²  + 0.5 KN/m²) = 2.923 KN/m² 

Per quanto  riguarda i carichi accidentali q_a, la normativa per il residenziale prevede 2 KN/m².
Inseriamo questi ultimi due dati nella tabella, e il valore della luce che è pari a 5m.

Il foglio di calcolo ci ha calcolato il q ultimo  come somma dei tre carichi (strutturale, permanente e accidentale) moltiplicati ognuno per un coefficiente di sicurezza dettato dalle normative, il tutto moltiplicato per l’interasse; inoltre viene calcolato anche il Momento massimo tenendo in considerazione che la trave è una trave appoggiata e che quindi M_max= ql²/8.

Il secondo passo è introdurre le tensioni caratteristiche del calcestruzzo e dell’acciaio f_yk (N/mm2) e f_ck (N/mm2) in base alla tipologia che scegliamo.
Nel nostro caso, scegliamo l’acciaio da armatura B450A  con  f_yk=450 e il calcestruzzo di classe C45/55 (C di Concrete) in cui il primo numero individua il valore caratteristico di resistenza cilindrica a compressione monoassiale f_ck =45 mentre il secondo identifica quella cubica Rck = 55.

Una volta inseriti i dati nella tabella Excel, otteniamo la resistenza di progetto dell’acciaio f_yd come il rapporto tra f_yk e il coefficiente parziale di sicurezza relativo all’acciaio da armatura di valore 1,15; mentre la resistenza di progetto del calcestruzzo f_cd viene calcolata come il rapporto tra f_ck e il coefficiente parziale di sicurezza per il calcestruzzo (pari a 1,5) il tutto moltiplicato per α= 0.85 (coefficiente riduttivo per le resistenze di lunga durata).

I valori β ed r vengono calcolati anche loro automaticamente in base ai risultati ottenuti; l’ultimo dato da inserire è la base, ipotizzando di mantenere un δ (copriferro dell’armatura inferiore) uguale a 5cm.

Ipotizziamo dunque una b= 25cm. Automaticamente, il foglio di calcolo trova l’altezza utile H_u e  dunque, sommandoci il δ, l’altezza minima H_min in cm. In base a questo valore, andiamo ad ingegnerizzare la trave inserendo il valore di H come la decina subito superiore di H_min e controllando che il foglio di calcolo dia “Verificato”.
La sezione così progettata risulta effettivamente verificata se oltre ai carichi già calcolati, è in grado di sopportare anche il peso proprio, di cui troviamo il valore alla fine della riga sui cui abbiamo lavorato fino ad ora.
Nella riga sottostante infatti, come possiamo notare, non vi sono presenti caselle azzurre, ovvero quelle modificabili, ma solo caselle di calcolo bianche. Proprio in questa riga, nella casella del carico ultimo, viene aggiunto al valore precedentemente calcolato il peso proprio moltiplicato per un fattore di sicurezza 1.3 e in base al risultato vengono rieffettutati tutti i calcoli fino ad arrivare ad una nuova H_min. Se il risultato di questi calcoli automatici porta ad una H_min comunque inferiore al valore ingegnerizzato, la trave è verificata.

(Questi calcoli con il peso proprio si effettuano solo sul cls in quanto le travi in legno e in acciaio hanno un peso proprio più piccolo tale da non far incrementare troppo il momento flettente.)
 

Proviamo a fare il calcolo adesso su una struttura in legno.

STRUTTURA IN LEGNO

Innanzitutto, notiamo dopo una prima occhiata al foglio di calcolo dedicato al legno, che i dati in questo caso da calcolare (ovvero le celle bianche) sono di meno rispetto al cemento armato, poiché andiamo a lavorare con un solo materiale. Avremo però dei coefficienti differenti, perché nel caso del legno bisogna tenere conto di determinati valori come l’umidità del luogo in cui opererà, o l’effetto della durata del carico.

I dati di cui necessitiamo sono quindi i seguenti:

• Interasse
• Carichi strutturali
• Carichi permanenti
• Carichi accidentali
• Luce
• f_m,k ovvero la resistenza caratteristica a flessione del legno scelto
• k_mod ovvero il coefficiente che tiene conto di umidità e tempo e che viene dato dalla normativa
• γ _m ovvero il coefficiente parziale di sicurezza dipendente dal materiale
• Base

Ipotizzando questa pianta di carpenteria e questa sezione di solaio, iniziamo a calcolare i carichi strutturali seguendo il procedimento utilizzato per il cemento armato:

Per trovare il peso specifico del legno, devo sceglierne una classe: utilizzo in questo caso il legno lamellare  GL24C, il più comunemente usato, che ha un peso specifico = 350kg/m³= 350 x 10^-2 KN/m³ = 3,5 KN/ m³ e una f_m,k = 24.

q_s Travetti: 2(0.2m x 0.1m x 1m)/m² x 3,5 KN/m³ = 0.14 KN/m²
q_s Tavolato: 0.035m x 0.1m x 1m/m² x 3,5 KN/m³ = 0.1225 KN/m²

q_s Tot: 0.14 KN/m²  + 0.1225 KN/m² = 0.2625 KN/m²

Per i carichi permanenti, i pesi specifici di cui necessitiamo sono:

Isolante: 30 Kg/m³ = 30 x 10^-2 KN/m³ = 0.3 KN/m³
Massetto alleggerito: 11 KN/m³
Pavimento legno duro: 850 kg/m³= 850 x 10^-3 KN/m³= 8,5 KN/m³

Calcoliamo:

q_p Isolante: (0.04m x 1m x 1m)/m² x 0.3 KN/m³ = 0.012 KN/m²

q_p Massetto: (0.03m x 1m x 1m)/m² x 11 KN/m³ = 0.33 KN/m²

q_p Pavimento legno duro: (0.02m x 1m x 1m)/m² x 8.5 KN/m³ = 0.17 KN/m²

q_p Tot= 0.012 KN/m² + 0.33 KN/m² + 0.17 KN/m²= 0.512 KN/m²  (+ 1 KN/m²  + 0.5 KN/m²) = 2.012 KN/m² 

Inseriamo nel foglio Excel interasse, carichi strutturali, carichi permanenti, carichi accidentali, luce e f_m,k = 24 (dato dalla normativa in base alla classe scelta).

Rimangono tre dati da inserire: K_mod, γ _m e la base.
Per quanto riguarda i primi due, essi sono dettati dalle normative; K_mod tiene conto della durata del carico a cui dovrà essere sottoposta la trave tramite le cinque “Classi di durata del carico” e delle condizioni climatiche in cui dovrà agire tramite le tre  “Classi di Servizio” ; γ _m invece è il coefficiente parziale di sicurezza relativo al materiale scelto.

Per quanto riguarda la base ipotizziamo  b=30.

Nel foglio di calcolo otterremo quindi questi risultati, con una Ingegnerizzazione di H= 55cm.

STRUTTURA IN ACCIAIO

Utilizziamo il procedimento fino ad ora seguito ed andiamo a calcolare i carichi strutturali e permanenti, sapendo che il peso specifico dell’acciaio è 78 KN/m³

• Carichi Strutturali

q_s IPE 100: (0.00103 m² x 1m) /m² x 78 KN/m³ = 0.08 KN/m²

q_s Lamiera Grecata  + Soletta: 9.16 Kg/m³  + 190 kg/m² = 199.16 Kg/m²= 1.9916 KN/m²

q_s tot: 0.08 KN/m² + 1.9916 KN/m²= 2.07194  KN/m²

• Carichi Permanenti

q_p Isolante: (0.04m x 1m x 1m)/m² x 0.3 KN/m³ = 0.012 KN/m²

q_p Massetto: (0.03m x 1m x 1m)/m² x 11 KN/m³ = 0.33 KN/m²

q_p Pavimento : (0.025m x 1m x 1m)/m² x 8.5 KN/m³ = 0.21 KN/m²

q_p Tot= 0.012 KN/m² + 0.33 KN/m² + 0.21 KN/m²= 0.5545 KN/m²  (+ 1 KN/m²  + 0.5 KN/m²) = 2.0545 KN/m² 

Dopo aver inserito i carichi, l’interasse e la luce all’interno della tabella Excel, viene calcolato il Momento ql^2/8 e non ci rimane altro che scegliere la nostra classe di resistenza.
Nel nostro caso, proviamo ad utilizzare la classe più bassa, ovvero l’acciaio S235 con una resistenza caratteristica f_y,k = 235.
Andando ad inserire questo valore, ci viene calcolata subito la tensione di progetto f_d = f_y,k / γ _s , in cui γ _s è il coefficiente parziale di sicurezza (simile a quello che abbiamo trovato nella tensione di progetto del legno) che in questo caso è = 1.05; viene calcolato inoltre il Modulo di resistenza a flessione W_xmin, che è uguale al rapporto tra il Momento massimo e la tensione di progetto f_d.

Controlliamo dunque nella tabella dei profilati IPE quale abbia un valore di W_xmin superiore a quello ottenuto e scopriamo così quale profilo è il più adatto alla situazione, nel nostro caso l’IPE 330.

Ovviamente, andando a scegliere una classe di resistenza dell’acciaio più alta, come ad esempio la S355, il modulo di resistenza a flessione risulterà più piccolo, essendo loro inversamente proporzionali, e potremmo scegliere un profilato con dimensioni più piccole, in questo caso sarebbe sufficiente una IPE 270 (tratteggiato nella tabella).

La prima esercitazione consiste nel dimensionare a flessione la trave più sollecitata appartenente ad un telaio di nostra scelta (uno in legno, uno in acciaio ed uno in cemento armato).  Il telaio scelto è composto da 4 campate: 2 (4 m di interasse x 4 m di luce) e 2 (4 m di interasse x 6 di luce). L'esercitazione si compone di tre analisi indipendenti, una per ogni sistema tecnologico.

                                                                             Dall'analisi del solaio, si può notare come la trave soggetta a maggior carico e di conseguenza al maggior momento flettente è quella messa in evidenza, infatti la sua area di influenza è pari a 24 mq (4 m interasse x 6 m luce).

FASI OPERATIVE:

1_ Analisi dei carichi distribuiti (KN/mq) 

    (peso specifico del materiale x volume) / 1 mq

I carichi distribuiti sono divisi in:

qs carichi strutturali: comprendono tutti gli elementi con funzione strutturale (escludendo il peso proprio della trave)

qp carichi permanenti: comprendono tutti gli elementi presenti sul solaio ma che non hanno una funzione strutturale

qa carichi accidentali: nominati dalla normativa tecnica e dipendono dalla destinazione d’uso (commerciale, residenziale ecc). 

2_ I carichi qs, qp e qa vengono sommati e moltiplicati per l’interasse per ottenere q (KN/m):

q= (1,3 x qs + 1,5 x qp + 1,5 x qa) x interasse

I singoli carichi vengono moltiplicati per dei coefficienti di sicurezza 1,3 e 1,5.

PRIMA TECNOLOGIA: il legno

Pesi specifici dei materiali che compongono il solaio:

Parquet: 8 KN/mc

Sottofondo: 18 KN/mc

Isolante in fibra di legno: 9 KN/mc

Caldana: 24 KN/mc

Tavolato: 6 KN/mc

Travetti: 5 KN/mc

1_ CARICHI STRUTTURALI qs

travetti (0.2 x 0.15 x 1) mc/mq x 5 KN/mc = 0.15 KN/mq

tavolato (0.04 x 1 x 1) mc/mq x 6 KN/mc = 0.24 KN/mq

totale qs (0.15 + 0.24) KN/mq = 0.39 KN/mq

2_ CARICHI PORTATI qp

tramezzi 1 KN/mq

impianti 0.5 KN/mq 

caldana (0.03 x 1 x 1) mc/mq x 24 KN/mc = 0.72 KN/mq

isolante (0.05 x 1 x 1) mc/mq x 9 KN/mc = 0.45 KN/mq

sottofondo (0.03 x 1 x 1) mc/mq x 18 KN/mc = 0.54 KN/mq

pavimento (0.02 x 1 x 1) mc/mq x 8 KN/mc = 0.16 KN/mq

totale qp (1 + 0.5 + 0.72 + 0.45 + 0.54 + 0.16) KN/mq = 3.37 KN/mq

3_ CARICHI ACCIDENTALI qa

ambiente ad uso residenziale 2 KN/mq

Questi valori ora attraverso il foglio excel vengono sommati tra loro per ottenere q (KN/mq).

q= (1,3 x qs + 1,5 x qp + 1,5 x qa) x interasse

q= (1,3 x 0.39 + 1,5 x 3.37 + 1,5 x 2) x 4 = 34.25 KN/m

Conoscendo il carico gravante sulla trave e la luce di questa si può ricavare il momento della trave appoggiata (M = q x l2/8).  M= 34.25 x 36/ 8= 154.12 KNm.

Per la realizzazione di questo solaio è stato scelto un legno lamellare GL24h con una resistenza caratteristica  f m,k = 24 MPa. si può calcolare quindi la resistenza di progetto f_d, e impostando la base della trave si ricaverà l’altezza. Una volta trovata h è opportuno ingegnerizzare l’altezza trovata in modo da ottenere una trave con una sezione standardizzata. 

L’altezza attraverso la formula di Navier è pari a 48,25 cm, per questo motivo ho scelto una trave con sezione 30 x 50 cm.

I calcoli precedenti però non tenevano in considerazione il peso proprio della trave, bisogna quindi ripetere i calcoli aggiungendo ai carichi strutturali qs il peso p, e verificare se la trave dimensionata 30 x 50 cm risulta adeguata. 

p = (0.3 x 0.5 x 1) mc/mq x 5 KN/ mc = 0.75 KN/mq

q= (1,3 x 0.39 + 1,5 x 3.37 + 1,5 x 2) x 4 + 1,3 x 0.75 = 35,23 KN/m

Una volta aggiunto il peso proprio della trave all’interno del foglio excel l’altezza ottenuta è pari a 48.93 cm.  Dal dimensionamento si nota che il calcolo precedentemente svolto era corretto: aggiungendo il peso della trave la sezione scelta 30 x 50 cm è in grado di sorreggere i carichi qs, qp e qa che gravano sul solaio. (sezione verificata)

SECONDA TECNOLOGIA: l’acciaio

Pesi specifici dei materiali che compongono il solaio:

Parquet: 8 KN/mc

Massetto: 18 KN/mc

Isolante: 9 KN/mc

Getto in cls: 24 KN/mc

Lamiera grecata: 0.10 KN/mq

Trave IPE 200: 78.5 KN/mc

Controsoffitto: 13 KN/mc

1_ CARICHI STRUTTURALI qs

travetti (0.00285 x 1) mc/mq x 78.5 KN/mc = 0.224 KN/mq

lamiera 0.10 KN/mq

getto cls (0.04 x 1 x 1) mc/mq x 24 KN/mc = 0.96 KN/mq

totale qs (0.224 + 0.1 + 0.96) KN/mq = 1.28 KN/mq

2_ CARICHI PORTATI qp

tramezzi 1 KN/mq

impianti 0.5 KN/mq 

massetto (0.03 x 1 x 1) mc/mq x 18 KN/mc = 0.54 KN/mq

isolante (0.04 x 1 x 1) mc/mq x 9 KN/mc = 0.36 KN/mq

pavimento (0.02 x 1 x 1) mc/mq x 8 KN/mc = 0.16 KN/mq

controsoffitto (0.01 x 1 x 1) mc/mq x 13 KN/mc = 0.13 KN/mq

totale qp (1 + 0.5 + 0.54 + 0.36 + 0.16 + 0.163) KN/mq = 2.69 KN/mq

3_ CARICHI ACCIDENTALI qa

ambiente ad uso residenziale 2 KN/mq

Questi valori ora, attraverso il foglio excel, vengono sommati tra loro per ottenere q (KN/mq).

q= (1,3 x qs + 1,5 x qp + 1,5 x qa) x interasse

q= (1,3 x 1.28 + 1,5 x 2.69 + 1,5 x 2) x 4 = 34.80 KN/m

Dalla tabella excel si ottiene un modulo di resistenza Wx pari a 597.86 cm3. Per questo motivo ho selezionato come profilo un IPE 330 con un Wx pari a 713.1 cm3.

Anche per la trave in acciaio i calcoli precedenti non tenevano in considerazione il peso proprio della trave, bisogna quindi ripetere i calcoli aggiungendo a q il peso p, e verificare se il profilo IPE 330 risulta adeguato.

p = (0.006261) mc/mq x 78.5 KN/ mc = 0.49 KN/mq

q = (1,3 x 1.28 + 1,5 x 2.69 + 1,5 x 2) x 4 + 1,3 x 0.49 = 35,44 KN/m

Nonostante nel primo predimensionamento non era stato considerato il peso proprio della trave, il profilo IPE 330 scelto risulta comunque idoneo. (Profilo IPE 330 verificato)

TERZA TECNOLOGIA: il cemento armato

Pesi specifici dei materiali che compongono il solaio:

Parquet: 8 KN/mc

Sottofondo: 18 KN/mc

Isolante in lana di roccia: 0.9 KN/mc

Getto in cls: 24 KN/mc

Travetto: 25 KN/mq

Pignatta: 8.7 kg

Intonaco: 18 KN/mc

1_ CARICHI STRUTTURALI qs

travetti (0.1 x 0.12 x 1) mc/mq x 25 KN/mc x 2 = 0.6 KN/mq

pignatte (8 x 8.7 kg/mq) = 67.2 kg/mq = 0.672 KN/mq

soletta collaborante (0.04 x 1 x 1) mc/mq x 24 KN/mc = 0.96 KN/mq

totale qs (0.672 + 0.6 + 0.96) KN/mq = 2.23 KN/mq

2_ CARICHI PORTATI qp

tramezzi 1 KN/mq

impianti 0.5 KN/mq 

massetto (0.03 x 1 x 1) mc/mq x 18 KN/mc = 0.54 KN/mq

isolante (0.04 x 1 x 1) mc/mq x 0.9 KN/mc = 0.036 KN/mq

pavimento (0.015 x 1 x 1) mc/mq x 8 KN/mc = 0.12 KN/mq

intonaco (0.01 x 1 x 1) mc/mq x 18 KN/mc = 0.18 KN/mq

totale qp (1 + 0.5 + 0.54 + 0.36 + 0.18 + 0.12) KN/mq = 2.37 KN/mq

3_ CARICHI ACCIDENTALI qa

categoria b2 - uffici aperti al pubblico 3 KN/mq

Questi valori ora, attraverso il foglio excel, vengono sommati tra loro per ottenere q (KN/mq).

q= (1,3 x qs + 1,5 x qp + 1,5 x qa) x interasse

q= (1,3 x 2.23 + 1,5 x 2.37 + 1,5 x 3) x 4 = 43.82 KN/mq

Per la realizzazione di questo solaio è stato scelto un acciaio con una resistenza caratteristica      f _y,k = 450 MPa e un calcestruzzo con resistenza a compressione R_ck pari a 50 MPa e impostyamdo una base di 30 cm avremo una altezza minima di 37,84 cm. Ingegnerizzo la sezione con b= 30cm e h= 40 cm.

Anche per la trave in cls i calcoli precedenti non tenevano in considerazione il peso proprio della trave, bisogna quindi ripetere i calcoli aggiungendo a q il peso p, e verificare se sezione risulta adeguato.

q trave (0.006261) mc/mq x 78.5 KN/ mc = 0.49 KN/mq

q= (1,3 x 2.23 + 1,5 x 2.37 + 1,5 x 2) x 4 + 1,3 x 0.49 = 44,46 KN/m

Nonostante nel primo predimensionamento non era stato considerato il peso proprio della trave, il profilo IPE 330 scelto risulta comunque idoneo.  (sezione 30 x 40 cm verificata)

                                                                  ESERCITAZIONE

La prima esercitazione prevede il dimensionamento della trave più sollecitata del telaio nelle tre tecnologie: legno, acciaio e cls armato. 

Osservando la struttura è evidente che la trave su cui grava più carico è quella centrale poiché la sua area è pari a 30 m², cioè:

Luce = 6m - Interasse = 5m

Trave in Legno

• Carichi strutturali della trave:

Travetto con sezione 12x22 cm e peso specifico pari a 6 kN/m³

                  q₁= (0,12 x 0,22 x 1) m³/m² x 6kN/m³ = 0,158 kN/m²

Tavolato con spessore 4 cm e peso specifico pari a 7 kN/m³

                  q₂= (0,04 x 1 x 1) m³/m² x 7kN/m³ = 0,28 kN/m²

calcoliamo il carico strutturale qs escludendo il peso proprio della trave principale:

qs = q₁ + q₂ = 0,158 kN/m² + 0,28 kN/m² = 0,438 kN/m²

• Carichi permanenti della trave:

Caldana alta 4 cm e peso specifico pari a 0,28 kN/m²

                               q₁ = 0,28 kN/m²

Isolante spessore 3,5 cm e peso specifico pari a 30 Kg/m³ =  0,3 kN/m³

                               q₂ = (0,035 x 1 x 1) m³/m² x 0,3 kN/m³ = 0,0105 kN/m²

Sottofondo alto 3 cm e peso specifico pari a 0,54 kN/m²

                               q₃ = 0,54 kN/m²

Pavimento in cotto spesso 2 cm e peso specifico pari a 18 kN/m³

                               q₄ = (0,02 x 1 x 1) m³/m² x 18 kN/m³ = 0,36 kN/m²

calcoliamo il carico permanente qp aggiungendo l’incidenza degli impianti e dei tramezzi:

qp = q₁ + q₂ + q₃ + q₄ = 0,28 kN/m² + 0,0105 kN/m² + 0,54 kN/m² + 0,36 kN/m² =

         1,19 kN/m² + 0,5 kN/m² + 1 kN/m² = 2,69 kN/m²

• Carichi accidentali qa della trave possono variare nel tempo e sono regolati dalle Norme Tecniche per le costruzione – del 2008.

Per questa esercitazioni consideriamo un edificio ad uso residenziale quindi:

qa = 2,00 kN/m²

Inserendo il valore di ogni singolo carico in un foglio excel darà come risultato il carico totale qu (kN/m) considerando che:

qu = [(qs x 1,3) + (qp x 1,5) + (qa x 1,5)] x interasse =

   = [(0,438 x 1,3) + (2,69 x 1,5) + (2,00 x 1,5)] x 5 = 38,02 kN/m

Inserendo la luce che è uguale a 6 m, possiamo ricavare il Momento massimo di una trave appoggiata  Mmax = ql²/8

Nella fase progettuale dobbiamo scegliere:

1– La tipologia di legno: Legno lamellare GL 24h con

     resistenza a flessione caratteristica fm,k = 24 MPa    

2 – coefficiente della durata del carico kmod = 0,8 (fornito dalla normativa)

3 – coefficiente parziale di sicurezza del materiale γm = 1,45 (legno lamellare)

Con questi dati possiamo calcolare la tensione ammissibile f_d (N/mm²) = fm,k x kmod / γm

4 – impostando la base b= 35 cm, ricaviamo l’altezza hmin

hmin è il valore minimo che deve avere l’altezza della sezione, tale va ingegnerizzato cioè va scelto un valore di altezza superiore ad hmin, cioè H= 50 cm

quindi non avendo considerato il peso proprio della trave è giusto scegliere la sezione con un profilo pari a 35 x 50 cm

Nella fase di verifica dobbiamo:

1 – dimensionare il carico della trave p (kN/m) e sommarlo al carico totale:

p = (0,35 x 0,50 x 1) m³/m x 6kN/m³ = 1,05 kN/m

Il nuovo carico qu, che comprende il peso della trave, può essere sostenuto da una trave con h = 47,90 cm con profilo rettangolare 35 x 50 cm.

                                               La sezione 35 x 50 cm è stata verificata!

Trave in Acciaio

• Carichi strutturali della trave:

Trave secondaria area della sezione 0,00285 m² e peso specifico pari a 78,5 kN/m³ (IPE 200)                  

                               q₁ = (0,00285 m² x 1 m) x  78,5 kN/m³ = 0,224 kN/m²

Lamiera gregata altezza 7,5 cm e peso specifico pari a 11 Kg/m² =  0,11 kN/m²

                               q₂ = 0,11 kN/m²

Getto di cls volume 0,07 m³ peso specifico pari a 24 kN/m³

                               q₃ = 0,07 m³/m² x  24 kN/m³ = 1,68 kN/m²

calcoliamo il carico strutturale qs:

qs = q₁ + q₂  +q₃ = 0,224 kN/m² + 0,11 kN/m² +  1,68 kN/m² = 2,01 kN/m²

• Carichi permanenti della trave:

Controsoffitto peso specifico pari a 0,3 kN/m²

                               q₁ = 0,3 kN/m²

Isolante altezza 4 cm e peso specifico pari a 35 Kg/m³ =  0,35 kN/m³

                               q₂ = (0,04 x 1 x 1) m³/m² x 0,35 kN/m³ = 0,014  kN/m²

Massetto spessore 3,5 cm e peso specifico pari a 18 kN/m³

                               q₃ = (0,035 x 1 x 1) m³/m² x 18kN/m³ = 0,63 kN/m²

Pavimento in ceramica peso specifico pari a 0,4 kN/m²

                               q₄ = 0,4 kN/m²

calcoliamo il carico permanente qp aggiungendo l’incidenza degli impianti e dei tramezzi:

qp = q₁ + q₂ + q₃ + q₄ = 0,3 kN/m² + 0,014 kN/m² + 0,63 kN/m² + 0,4 kN/m² =

         1,34 kN/m² + 0,5 kN/m² + 1 kN/m² = 2,84 kN/m²

• Carichi accidentali qa della trave possono essere variabili nel tempo e sono regolati dalle Norme Tecniche per le costruzione – del 2008. Per questa esercitazioni consideriamo un edificio ad uso residenziale quindi:

qa = 2,00 kN/m²

Inserendo il valore di ogni singolo carico in un foglio excel darà come risultato il carico totale qu (kN/m) considerando che:

qu = [(qs x 1,3) + (qp x 1,5) + (qa x 1,5)] x interasse =

   = [(2,01 x 1,3) + (2,84 x 1,5) + (2,00 x 1,5)] x 5 = 49,37 kN/m

Inseriamo la luce che è uguale a 6 m, così da ricavare il Momento massimo di una trave appoggiata  Mmax = ql²/8

Fase progettuale:

la tensione di snervamento del Fe 430/ S275 è fy,k = 275 MPa quindi:

dai risultati ottenuti con modulo di resistenza pari a Wx,min = 848,18 cm³ è opportuno selezionare come profilo un IPE 360.

Fase di verifica:

calcoliamo il carico q della trave aggiungendo il peso della trave p moltiplicandolo per 1,3.

Sezione della Trave IPE 360 = 72,70 cm²

p = (0,00727 x 1) m³/m² x 78,5 kN/m³ = 0,57 kN/m

Il nuovo carico qu, che comprende il peso della trave, può essere sostenuto da una trave IPE 360 dato che il valore di Wx,min non supera quello Wx scelto.

                                            Il profilo IPE 360 è stato verificato!

Trave in CLS armato

• Carichi strutturali della trave:

Pignatta n°8 di pignatte e peso specifico pari a 8 Kg

                               q₁ = 8 x 8 Kg/m² = 64 Kg/m² = 0,64 kN/m²

Soletta in cls altezza 4 cm e peso specifico pari a 24 kN/m³

                               q₂ = (0,04 x 1 x 1) m³/m² x 24 kN/m³ = 0,96 kN/m²

Travetti altezza 16 cm e peso specifico pari a 24 kN/m³

                               q₃ = 2 x(0,16 x 0,1 x1)m³/m² x  24 kN/m³ = 0,768 kN/m²

calcoliamo il carico strutturale

qs = q₁ + q₂  +q₃ = 0,64 kN/m² + 0,96 kN/m² +  0,768 kN/m² = 2,368 kN/m²

• Carichi permanenti della trave:

Intonaco spessore 1cm e peso specifico pari a 16 kN/m³

                              q₁ = (0,01 x 1 x 1)m³/m² x 16 kN/m³ = 0,16 kN/m²

Isolante altezza 4 cm e peso specifico pari a 35 Kg/m³ =  0,35 kN/m³

                              q₂ = (0,04 x 1 x 1) m³/m² x 0,35 kN/m³ = 0,014  kN/m²

Massetto spessore 3,5 cm e peso specifico pari a 2000 Kg/m³ =  20 kN/m³

                              q₃ = (0,035 x 1 x 1) m³/m² x 20 kN/m³ = 0,7 kN/m²

Pavimento in cotto  peso specifico pari a 28 Kg/m²

                              q₄ = 0,28 kN/m²

calcoliamo il carico permanente qp aggiungendo l’incidenza degli impianti e dei tramezzi:

qp = q₁ + q₂ + q₃ + q₄ = 0,16 kN/m² + 0,014 kN/m² + 0,7 kN/m² + 0,28 kN/m² =

         1,154 kN/m² + 0,5 kN/m² + 1 kN/m² = 2,654 kN/m²

• Carichi accidentali qa della trave possono essere variabili nel tempo e sono regolati dalle Norme Tecniche per le costruzione – del 2008.

Per questa esercitazioni consideriamo un edificio ad uso residenziale quindi:

qa = 2,00 kN/m²

Inserendo il valore di ogni singolo carico in un foglio excel darà come risultato il carico totale qu (kN/m) considerando che:

qu = [(qs x 1,3) + (qp x 1,5) + (qa x 1,5)] x interasse =

   = [(2,368 x 1,3) + (2,654 x 1,5) + (2,00 x 1,5)] x 5 = 50,30 kN/m

Inseriamo la luce che è uguale a 6 m, così da ricavare il Momento massimo di una trave appoggiata  Mmax = ql²/8

Fase progettuale:

1 - acciaio per il cls: B450C avremo come tensione di snervamento fyk = 450 MPa, con queste scelte è possibile ricavare la tensione di progetto con la formula:           

fyd = fyk / γs

2 –tensione di progetto del cls fcd = αcc x fck/γc

3 – β = 0,53 e r = 2,14

4 – consideriamo una base b = 30 cm

otteniamo un Hmin pari a 36,09 cm, quindi ingegnerizzando possiamo scrivere H = 40 cm.

Quindi la sezione finale della trave in cls sarà 30 x 40 cm.

Fase di verifica:

Come per la trave in legno e in acciaio è opportuno calcolare il carico q della trave in cls, quindi calcoliamo il peso unitario:

p = (0,30 x 0,40 x 1) m³/m² x 25 kN/m³ = 3 kN/m²

quindi il carico totale con l’aggiunta del peso proprio del cls moltiplicato per 1,3 è

qu = 54,20 kN/m.

                                  La sezione 30 x 40 cm è stata verificata!

Si ipotizza il solaio in figura come un solaio di un edificio ad uso residenziale e, dopo aver scelto le componenti delle tre diverse tecnologie da analizzare, si procede con il dimensionamento della trave più sollecitata per ciascun caso.

La trave più sollecitata è quella dell’allineamento B, che ha un’area di influenza pari A = 7x5= 35 mq.

LEGNO

Si calcolano i carichi strutturali, permanenti e accidentali.

(qs) carichi strutturali ( per il momento si esclude la trave):

Travetti:  5 KN/mc * 2*(0,12 * 0,25 * 1) mc/mq = 0,3 KN/mq

Tavolato di legno: 6 KN/mc * (0,035 * 1 * 1) mc/mq = 0,21 KN/mq

qs = 0,3 KN/mq +  0,21 KN/mq = 0,51 KN/mq

(qp) carichi permanenti:

Cls caldana: 24 KN/mc * (0,04 * 1 * 1) mc/mq = 0,96 KN/mq

Isolante: 0,2 KN/mc * (0,04 * 1 * 1) mc/mq = 0,08 KN/mq

Sottofondo: 18 KN/mc * (0,03 * 1 * 1) mc/mq = 0,54 KN/mq

Parquet: 7,5 KN/mc * (0,018 * 1 * 1) mc/mq = 0,135 KN/mq

Impianti: 0,5 KN/mq

Tramezzi: 1 KN/mq

qp = (0,96 + 0,08 + 0,54 + 0,135 + 1,5) KN/mq =3,215 KN/mq

(qa) carico accidentale:

civile abitazione: 2 KN/mq  

(qtot) carico totale = qs + qp + qa

qtot = (0,51 + 3,215 + 2)KN/mq = 5, 725 KN/mq 

Carico che agisce sulla trave considerata:

qu = (1,3*qs + 1,5*qp + 1,5*qa)*i

q_u= 42,43 KN/m

Si può quindi calcolare il M_max, seguendo il modello della trave appoggiata: M_max = 259,87 KNm

Si sceglie di realizzare il solaio con un legno lamellare GL24C (f_m,k = 24 N/mm²), con una classe di durata lunga e una classe di servizio 2, quindi il k_mod = 0,70.

Si calcola poi la resistenza di progetto, definita dal prodotto della resistenza caratteristica del legno f_m,k per il coefficiente di degrado nel tempo k_mod diviso il coefficiente di sicurezza g_m:

s_adm=f_d = (24 N/mm² * 0,70)/1,45 = 11,59 N/mm²

DIMENSIONAMENTO TRAVE:

Si imposta la base della trave di 35 cm e si ricava l’altezza.

Si inseriscono i dati nella tabella Excel per dimensionare la trave.

L’altezza minima della trave deve essere di 62,01 cm infatti:

b= 35 cm

W_x= M_x/f_d

Per una sezione rettangolare omogenea W_x = 1/6*b*h

h = √[(6M_x)/(b*f_d)] = l*α

Si prende una sezione di 35x65 cm.

VERIFICA:

Si verifica la dimensione della trave principale, aggiungendo il peso proprio della trave al carico totale al metro lineare, cioè qtot moltiplicato per l’interasse.

Peso specifico trave: 5KN/mc

Area sezione trave: A= (0,35 * 0,65) mq = 0,23 mq

Coefficiente di sicurezza: 1,3

Carico lineare della trave: 5KN/mc *0,23 mq * 1,3 = 1,5 KN/m

q = qu (solaio) + carico lineare trave

q = 42,43 KN/m + 1,5 KN/m = 43,96 KN/m

Si ottiene come valore di h_min = 63,12 cm < 65 cm, quindi la sezione è verificata.

ACCIAIO

(qs) carico strutturale (per il momento si escludono i travetti):

Lamiera grecata: 0,105 KN/mq

Getto di completamento: 24 KN/mc * 0,12 mc/mq = 2,88 KN/mq

qs = (0,105 + 2,88) KN/mq = 2,98 KN/mq

(qp) carichi permanenti:

Pavimento: 3,125 KN/mq

Massetto: 19 KN/mc * 0,03 mc/mq = 0,57 KN/mq

Rete elettrosaldata: 0,54 KN/mq

Impianti: 0,5 KN/mq

Tramezzi: 1 KN/mq

qp = (3,125 + 0,57 + 0,54 + 1,5) KN/mq =  5,73 KN/mq

(qa) carico accidentale:

Civile abitazione: 2KN/mq

(qu) carico ultimo:

qu = (1,3*qs + 1,5*qp + 1,5*qa)* i

qu = (2,98*1,3+5,73*1,5+2*1,5) KN/mq * 5 m= 77,54 KN/m

Dimensionamento travetti:

Si considera un interasse di 1 m e una luce di 6 m.

L’acciaio scelto è del tipo Fe 360/ S 235

Il valore ottenuto dalla tabella Excel è W_x= 311,03 cm³ quindi si sceglie una trave Ipe 240, con W_x=324,3 cm³

VERIFICA:

Per verificare si somma al qs il peso relativo ai travetti.

Peso travetti: 7,85 KN/mc * 0,0039 mq = 0,03 KN/m

qs + qtravetti = (2,98 + 0,03 )KN/mq = 3,01 KN/mq

La sezione è verificata poiché 311,81 cm³<324,30 cm³.

DIMENSIONAMENTO TRAVE:

Luce: 7 m

Interasse: 5 m

Area di influenza: 35 mq

Si utilizzano i valori di carico trovati precedentemente, comprendendo anche il peso dei travetti.

Si inseriscono la luce della trave e l’interasse.

A parità di luce, carichi ed interassi, si preferisce un acciaio con f_yd= 275 N/mm², che permette di avere una trave più snella, infatti si può utilizzare un profilato Ipe 500 con W_x= 1930 cm³, invece di un Ipe 550 che sarebbe necessario se scegliessimo l’acciaio S235.

VERIFICA DEL DIMENSIONAMENTO:

Si deve aggiungere al qu il carico lineare della trave.

Peso specifico acciaio: 78,5 KN/mc

Area Ipe 500: 116 cm² = 0,0116 mq

Coefficiente di sicurezza: 1,3

q = 78,5 KN/mc * 0,0116 mq * 1,3 = 1,18 KN/m

qtot = (77,54 + 1,18) KN/m =  78,72 KN/m

Il modulo di resistenza W_x = 1841 cm³< 1930 cm³ dell’Ipe 500. Quindi il dimensionamento è verificato.

CEMENTO ARMATO

(qs ) carichi strutturali:

Soletta: 24 KN/mc * 0,04 mc/mq = 0,96 KN/mq

Travetti: 24 KN/mc * 2 * (0,16*0,10) mc/mq = 0,768 KN/mq

Pignatte: 0,091 KN/mq * 8 = 0,728 KN/mq

qs = (0,96 + 0,768 + 0,728) KN/mq = 2, 456 KN/mq

(qp) carichi permanenti:

Pavimento: 20 KN/mc * 0,04 mc/mq = 0,8 KN/mq

Massetto: 19 KN/mc * 0,04 mc/mq = 0,76 KN/mq

Isolante: 0,2 KN/mc * 0,04 mc/mq = 0,008 KN/mq

Intonaco: 18 KN/mc * 0,01 mc/mq = 0,18 KN/mq

Tramezzi : 1 KN/mq

Impianti: 0,5 KN/mq

qp = (0,8 + 0,76 + 0,008 + 0,18 + 1,5) KN/mq = 3,248 KN/mq ≅ 3,25 KN/mq

(qa) carichi accidentali:

Civile abitazione: 2 KN/mq

qu = (1,3*2,456 + 1,5*3,25 + 1,5*2) KN/mq * 5m = 55,34 KN/m

DIMENSIONAMENTO TRAVE

Luce= 7 m

Interasse= 5 m

Per l’armatura si tiene conto di un acciaio con f_yk = 450 Mpa.

Si sceglie un calcestruzzo ordinario C35/45.

Scegliendo una base di 30 cm e un copriferro di 5 cm, si ottiene h_min= 57,15, quindi è stata data come altezza della trave h= 65 cm.

Si ha dunque una trave 30x65 cm, di A= 1950 cm².

VERIFICA

Si aggiunge al qu del solaio il carico al metro lineare della trave principale.

qtrave: 25 KN/mc * 0,195 mq = 4,88 KN/m

qtot = qsolaio + qtrave = 55,34 KN/m + (1,3*4,88) KN/m = 61,68 KN/m

Il valore di h_min= 63,60 cm, quindi la sezione è verificata in quanto 63,60 cm < 65 cm.

Se il valore di h_min fosse venuto maggiore di 65 cm, si sarebbe dovuto tornare indietro, cambiando i valori della luce, o della base o cambiando la classe del cls.