SdC(b) (LM PA)

Per la quarta esercitazione si calcola la rigidezza di un impalcato costituito da sei telai di cemento armato basati sul modello teorico "shear-type". La distanza tra il centro delle rigidezze rispetto al centro di massa determina la sua capacità di rispondere alle sollecitazioni orizzontali. L'impalcato, considerato di un piano solo, è il seguente:

I pilastri sono di sezione rettangolare 30x65 cm, alcuni disposti lungo x, altri lungo y, uno, invece, è a basa quadrata di 30x30 cm.

Il primo step della tabella excell richiede i valori della geometria e i materiali dei telai: l'altezza h=3,50m, il modulo plastico E (da materiale, 21000 N/mmq) e i momenti d'inerzia I (per la sezione rettangolare (b*h³)/12)
La tabella, quindi, calcola la rigidezza traslante di ogni telaio , che si ottiene dalla formula: 

Dove la rigidezza del singolo pilastro è dato dal modello  "shear-type"e vale 12*E*I/h³.

Si può assumere che ogni telaio è in grado di resistere a sforzi orizzontali al suo sviluppo (possiamo quindi rappresentare ogni telaio con una molla che ostacola gli spostamenti):

Si passa ora a calcolare le coordinate X e Y del centro d'area G, riducendo la forma in pianta in schemi semplici composti da rettangoli i quali centri G1 e G2, inseriti nella formula per il centro di un sistema di vettori paralleli, restituiscono il centro d'area di tutto l'impalcato.

Un telaio ben progettato richiede una distanza tra i due centri non troppo elevata,per limitare la rotazione rigida dell'impalcato e i conseguenti momenti torcenti sui pilastri, sottoponendo la struttura a sola traslazione pura. La distanza dell'impalcato considerato è tuttavia accettabile, anche se tende comunque a ruotare. Con il foglio excell calcoliamo, quindi, la rigidezza torsionale, mediante l'utilizzo della seguente formula che tiene in considerazione la distanza dei controventi dal centro delle rigidezze.

La rigidezza torsionale totale vale 15036062,80 KNm.

Con lo step 5 si calcola l'entità del carico sismico dell'impalcato, per il quale è necessario conoscere i carichi strutturali qs, i carichi permanenti non strutturali qp ed i carichi accidentali qa.
Per un normale solaio in latero-cemento, ad uso residenziale:
qs=1,86 KN/mq, qp=1,91 KN/mq, qa=2 KN/mq.

I carichi moltiplicati per l'area totale dell'impalcato forniscono G = 626,4 KN e Q = 216 KN, a loro volta vengono sommati (ma Q prima è moltiplicato per il coefficiente di contemporaneità 0,3 tabellato per uso residenziale) per avere il valore del peso sismico W = 691,2 KN. 
infine è necessario "accellerare" la massa dell'edificio per il coefficiente d'intensità sismica c, che dipende dall'area geografica e dalla sua sismicità (in questo caso vale 0,1) fino ad ottenere lo sforzo sismico orizzontale F= 69,12 KN.

Gli step 6 e 7 calcolano i valori degli spostamenti orizzontali e verticali e della rotazione dell'impalcato applicando la forza F sul centro di massa G, rispettivamente lungo l'asse X e lungo l'asse Y, con le formule qui riportate:

Il momento torcente M che appare nella tabella 6 ha come forza la forza sismica F e come braccio la distanza tra centro di massa e centro delle rigidezze, e vale quindi 52,89 KNm ed è antiorario nel caso di una forza fisica orizzontale, invece -85,51 ed è orario nel caso di una forza fisica verticale.

Nelle due tabelle finali si può calcolare la forza sismica agente sui singoli controventi orizzontali e verticali.
Nel caso di forze lungo X con le seguenti formule:

Lo stesso principio si applica con la forza lungo Y:

Per la terza esercitazione ci è stato richiesto di dimensionare una trave, non più appoggiata-appoggiata, bensì a mensola.
I solai sono gli stessi dell'esercitazione precedente e i materiali utilizzati saranno legno Gl 24c, acciaio Fe 430/S275, calcestruzzo C 25/30 con barre d’acciaio B450A.
Lo scopo è quello di effettuare su queste tre mensole la verifica a deformabilità, controllando l’abbassamento minimo dell’elemento strutturale in rapporto alla sua luce. 

Per la terza esercitazione ci è stato richiesto di dimensionare una trave, non più appoggiata-appoggiata, bensì a mensola.
I solai sono gli stessi dell'esercitazione precedente e i materiali utilizzati saranno legno Gl 24c, acciaio Fe 430/S275, calcestruzzo C 25/30 con barre d’acciaio B450A.
Ila verificherà sarà effettuata allo Stato Limite d’Esercizio (SLE), differentemente da quanto avvenuto invece per il dimensionamento delle travi nella precedente esercitazione, che ha avuto luogo allo Stato Limite Ultimo (SLU). Ipotizziamo in tutti e tre i casi di trovarci dinnanzi ad una mensola di lunghezza l e caricata con un carico uniformemente distribuito pari a qu. Il momento massimo nella sezione di incastro vale:

Mmax=(qu*l²)/2

Lo spostamento massimo verticale, invece, vale:
vmax= - (qe*l⁴)/8*E*Ix

Verificando che il rapporto tra la luce della trave ed il suo spostamento massimo sia maggiore di 250 possiamo stabilire che la trave non si deformerà più di quanto non sia consentito dalla normativa.

1) TRAVE IN LEGNO

2) TRAVE DI ACCIAIO

3) TRAVE IN CEMENTO ARMATO

Nel caso del cemento armato è necessario verificare che il peso stesso della trave, aggiunto al carico del solaio, non vada a sovraccaricare eccessivamente la struttura a mensola.

Per la seconda esercitazione andremo a dimensionare la trave maggiormente sollecitata di un impalcato strutturale ad uso residenziale. Calcoliamo quanto pesa un metro quadro del nostro solaio (espresso come densità di carico superficiale in kN/m²). Studieremo il caso di un salaio di legno, uno di laterocemento e uno di acciaio con lamiera grecata.
Divideremo il carico totale in qs (kN/m²) (carico dovuto al peso della struttura), il carico permanente qp (kN/m²) (carico di tutto ciò che grava sulla struttura), e il carico accidentale qa (kN/m²) (in questo caso 2,0 kN/m² cioè il carico accidentale previsto da normativa per gli edifici residenziali). 
Per calcolare il peso al metro quadro del solaio sommiamo tutti i pesi di tutti gli elementi tecnologici presenti. Il loro peso specifico (kN/m³) si moltiplica per la quantità di volume del materiale presente in un metro quadro (m³/m²). Dal calcolo si ottengono i pesi espressi in kN/m² che sommati individueranno i nostri qp e qs.
La normativa impone l'utilizzo di coefficienti moltiplicativi dei singoli carichi, che forniscono il carico totale come una combinazione di carico, espressa dalla formula seguente: qtot [KN/m²] = 1,3*qs + 1,5*qp + 1,5*qa  per lo stato limite ultimo con cui vanno calcolati. Da questo carico dobbiamo ricavare il carico agente sulla trave (qu) derivante dalla moltiplicazione di qtot per l'interasse della trave. A questo punto bisogna determinare il momento massimo agente sulla trave Mmax = qul²/8 (considerando il modello di trave appoggiata appoggiata).
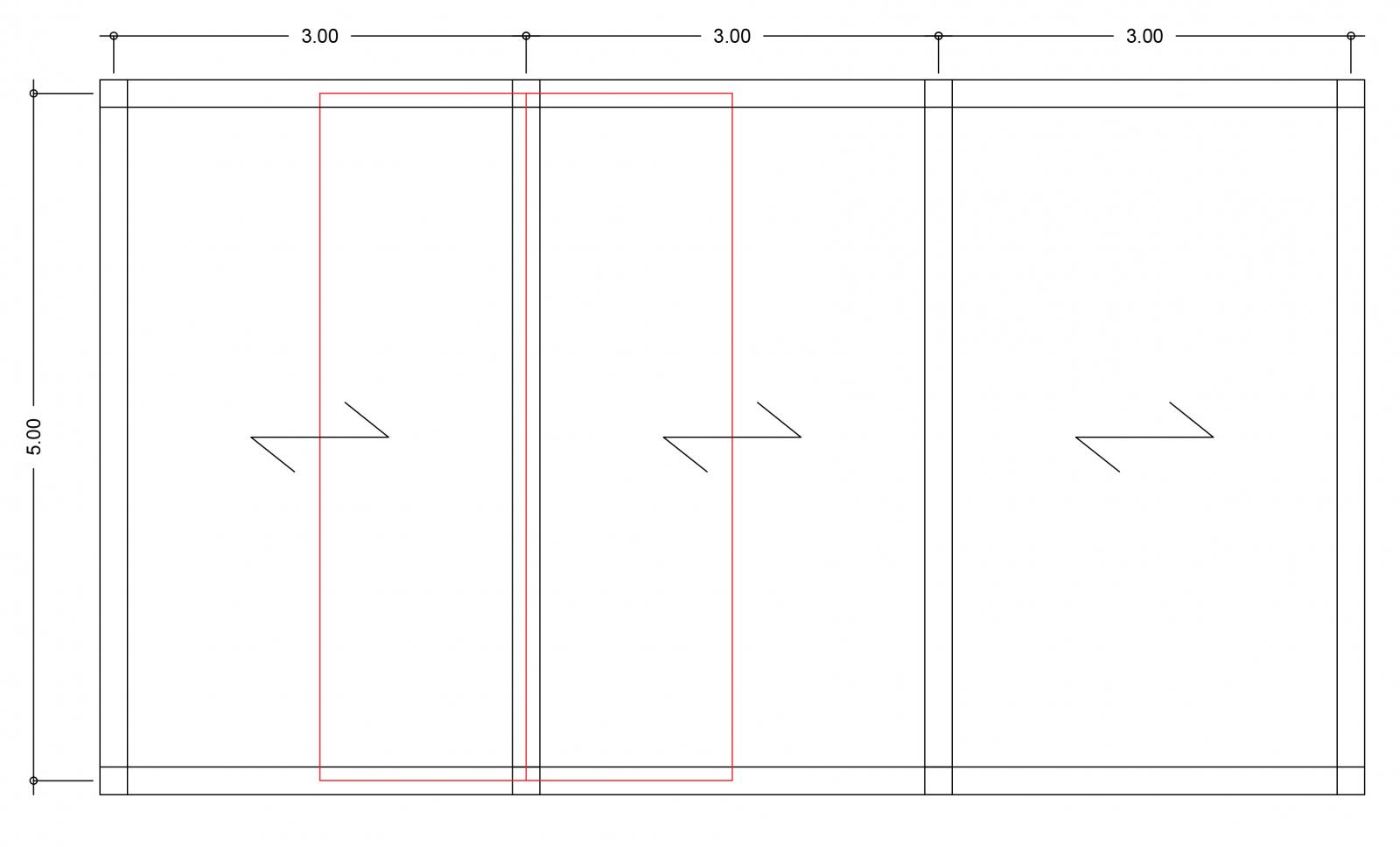
L'impalcato che andremo ad analizzare è il seguente, la trave analizzata è evidenziata in rosso e la sua area di influenza è di 15mq.

1)    TRAVE IN LEGNO

Nel dimensionamento di una sezione di una trave in legno il progettista deve scegliere il tipo di legno da utilizzare e quindi inserire nella colonna corrispondente la resistenza caratteristica a flessione fm,k del legno prescelto a seconda della tecnologia (legno massiccio o legno lamellare) e ad una classe di resistenza. 

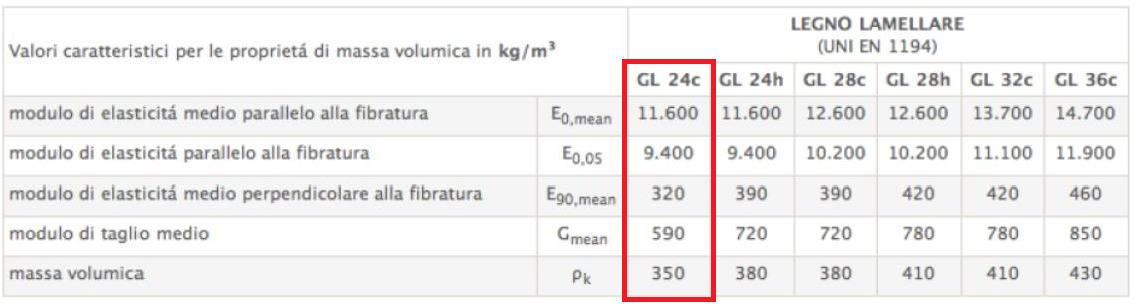
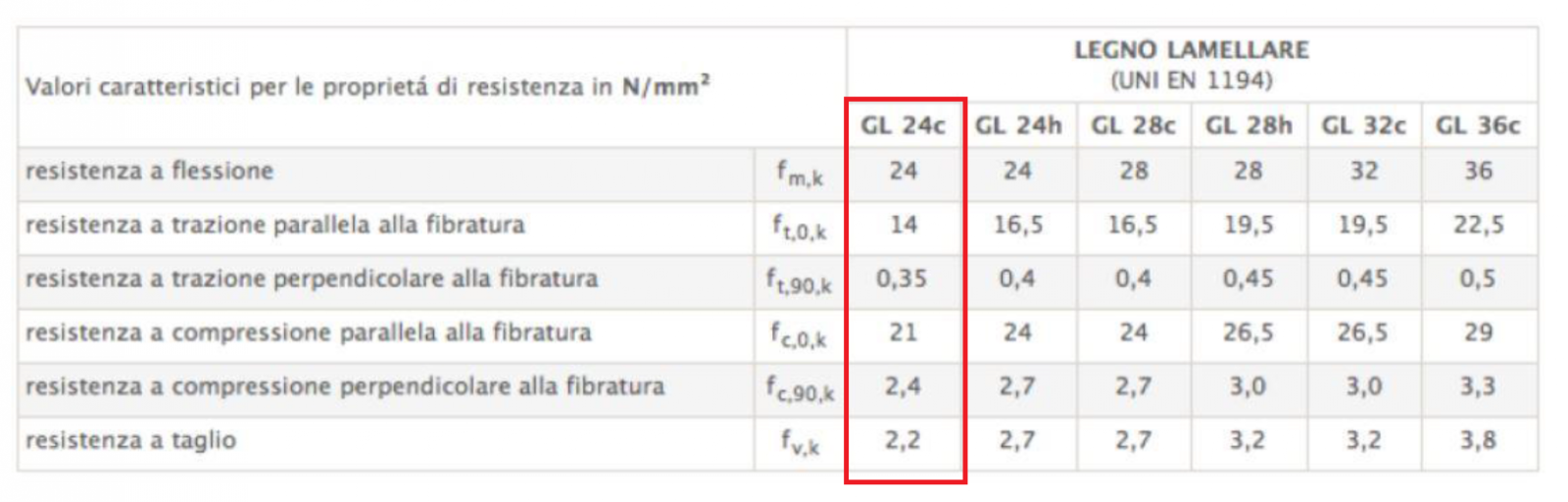
Consideriamo il GL 24c ed inseriamo nella tabella Excel la resistenza caratteristica a flessione fm,k.

La tensione di resistenza fd sarà a sua volta pari a fd = (kmod*fm,k)/γm

Kmod è un coefficiente diminutivo che considera l’effetto della durata del carico e le condizioni di umidità.

Ipotizzando un carico permanente, una classe di servizio 2 e un legno lamellare, avremo un valore kmod pari a 0,6 (come da normativa).

Il coefficiente γm è invece un coefficiente parziale di sicurezza del materiale e vale 1,45

Ora, con il foglio excell fornitoci, andiamo a calcolare la sezione della trave di legno. Inseriamo le informazioni sulla geometria dell'impalcato, le caratteristiche del materiale e le tensioni di progetto, calcoliamo il momento massimo e con la tensione di resistenza e una base di partenza di 40cm andiamo a calcolare l'altezza minima. 

hmin= (Mmax/b)^0.5 * (6/fd)^0.5 = 36,08 cm.

Ingegnerizzando l'altezza minima scegliamo un profilo quadrato di 40x40cm.

2) TRAVE IN ACCIAIO

Per dimensionare la sezione in acciaio procediamo individuando il modulo di resistenza a flessione minimo da utilizzare affinché la tensione del materiale non superi la tensione di progetto. 

fyd è la tensione di progetto e si calcola a partire dalla tensione caratteristica di snervamento divisa per un coefficiente di sicurezza γs pari a 1,05.

Fyd = Fyk/γs

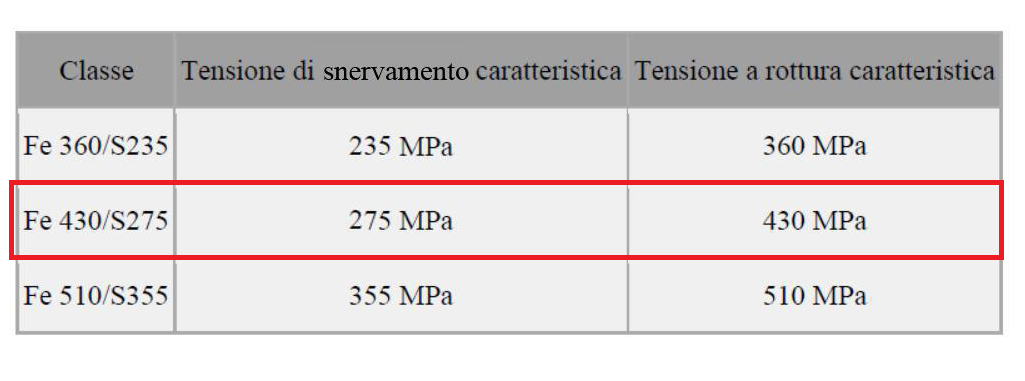
Se consideriamo l'acciaio Fe 430/S275, con una tensione di snervamento caratteristica di 275 MPa, otteniamo un Wx,min di 338,12 cm³.
 
Wx,min = Mmax/fyd

Wx,min è il valore minimo della sezione che posso scegliere per il dimensionamento. Con un Profilario di IPE in acciaio scegliamo una sezione con un Wx più grande.
La IPE270 con Wx = 429 cm³.

3) TRAVE IN CEMENTO ARMATO

In questo caso teniamo conto delle due diverse tensioni di progetto: del cls (fcd) e dell’acciaio (fyd).

Scelta una base, determinato il Momento massimo e δ (5cm) possiamo proseguire con la scelta della sezione da utilizzare.

Iniziamo scegliendo il tipo di acciaio ed il tipo di calcestruzzo, individuando prima fyk ed fck (le resistenze caratteristiche), poi li riduciamo ottenendo fcd e fyd (le tensioni di progetto del calcestruzzo e dell’acciaio)

fyd = fyk/γs             fcd = αcc(fck/γc)

γs  è il coefficiente parziale di sicurezza relativo all’acciaio (pari a 1,15), αcc è il coefficiente riduttivo per le resistenze di lunga durata (0,85) e γc il coefficiente parziale di sicurezza relativo al cls, pari a 1,5.

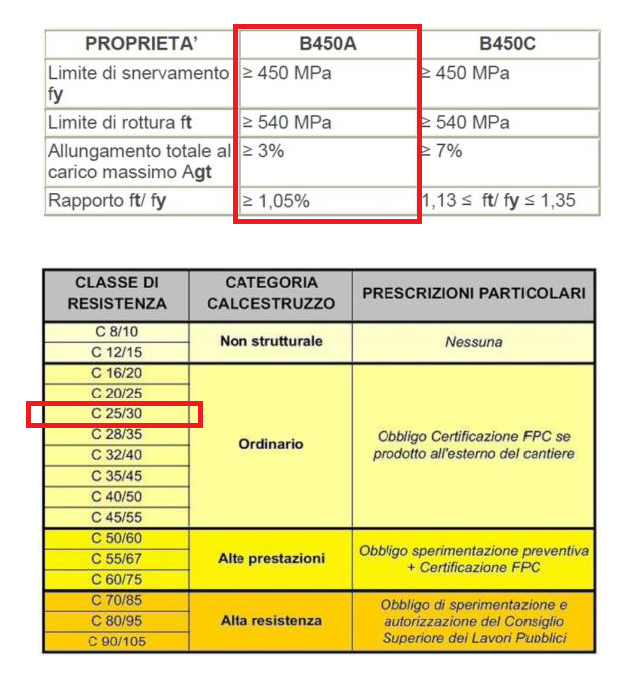
Scegliamo un acciaio B450A (con fyk = 450 MPa) ed un calcestruzzo ordinario C 25/30 (fck = 30 MPa).

Scegliendo la base della sezione di 30cm e noti i valori delle tensioni di progetto, determiniamo hu (l’altezza utile della sezione, pari all’altezza totale meno δ), da cui poi otterremo appunto una Hmin (altezza minima della sezione).

Hmin = hu + δ

hu = r(Mmax/b)^0.5    con r = (2/[fcd*(1-β/3)*β])^0.5      e     β= fcd/(fcd+fyd/n)

L’altezza minima andrà poi ingegnerizzata in eccesso. Nel nostro caso quindi, ottenendo una hu = 33,42 cm avremo una Hmin= 38,42cm, che ingegnerizziamo prendendo un’altezza H = 40cm.

A questo punto è necessario aggiungere al carico totale qu il peso stesso della trave (calcolato con il peso specifico del cls armato che è pari a 3 kN/m). Se l’altezza minima risultante sarà ancora minore dell’altezza ingegnerizzata la sezione risulterà verificata anche una volta aggiunto il peso proprio della trave.
Da qui la necessità di aumentare l'altezza della sezione H=45cm.

Questa esercitazione è finalizzata a calcolare come viene ripartita una forza orizzontale, come può essere il vento o il sisma, su un generico impalcato strutturale ad un piano. Calcoleremo quindi le rigidezze dei controventi, il centro d’area e il centro delle rigidezze dell’impalcato trovando così gli spostamenti prodotti dalla forza.

L’impalcato preso in considerazione è costituito da telai piani in cemento armato con controventi di tipo Shear-type, la cui caratteristica è di avere travi infinitamente rigide questo fa sì che ai pilastri non vengano trasmesse rotazioni.

Per prima cosa poniamo l’impalcato in un sistema di riferimento cartesiano dove andiamo ad individuare i telai paralleli all’asse y e quindi verticali e i telai paralleli all’asse x quindi orizzontali:

Telaio 1v  composto da: pilastri  1, 7 e 11

Telaio 2v  composto da: pilastri  2, 4 e 8

Telaio 3v  composto da: pilastri  9 e 12

Telaio 4v  composto da: pilastri  3 e 5

Telaio 5v  composto da: pilastri  6 e 10

 Telaio 1o composto da: pilastri  1, 2 e 3

 Telaio 2o composto da: pilastri  4, 5 e 6

 Telaio 3o composto da: pilastri  7, 8, 9 e 10

 Telaio 4o composto da: pilastri  11 e 12

I controventi, che per il solaio rappresentano vincoli cedevoli elasticamente, possono essere schematizzati nel piano dell'impalcato come molle, aventi un’adeguata rigidezza.

Trattandosi di telai shar-type la loro rigidezza sarà data da:

Quindi in generale per un telaio di n pilastri la rigidezza sarà: 

Dove E rappresenta il modulo elastico del cls armato mentre I è il momento d’inerzia del pilastro secondo la direzione in cui resiste meglio. 

quindi per il pilastro da noi adottato avremo: 

Iy=(30*40^3)/12=160000

Ix=(40*30^3)/12=9000

Andiamo ora a calcolare la rigidezza traslante associata ad ogni controvento sapendo che l’altezza di ogni nostro pilastro è di 3,5 m e il modulo elastico del nostro materiale  è di 21000 N/mm^2.

Una volta definita la rigidezza di ogni controvento le riportiamo in tabella insieme alla sua distanza dall’origine. 

Ora vediamo come calcolare il centro di massa dell’impalcato (G).

Innanzi tutto dividiamo l’impalcato in forme geometriche elementari come i rettangoli, nel nostro caso tre, di cui definiamo l’area e il baricentro:

Area A: 11,70 m²

Area B: 6,43 m²

Area C:  8,43 m²

Centro A: (1,5 ;  3,9)

Centro B: (4,6 ;  2,9)

Centro C: (2,5 ;  0,97)

Applichiamo ora attraverso il foglio Excel la formula della sommatoria per trovare il centro di massa che risulta avere coordinate G (2,58 ; 2,73).

Definiamo ora le coordinate del centro delle rigidezze (Xc, Yc) attraverso la sommatoria che moltiplica le rigidezze traslanti  (kv, ko) per la distanza del controvento dall’origine (dv, do). 

Ricaviamo ora il valore delle rigidezza torsionale calcolando tutte le distanze dei diversi controventi (ddv, ddo) dal centro delle rigidezze (C) data dalla formula:

Nella tabella successiva possiamo calcolare il valore della forza sismica agente  sull’impalcato attraverso l’analisi dei carichi sismici.

Per far ciò riprendiamo i valori dei carichi strutturali, permanenti, e accidentali dell’esercitazione sul dimensionamento della trave:

q_s = 3,12 KN/m²

q_p = 3,95 KN/m²

q_p  = 2,00 KN/m²

Attraverso il foglio Excel e il valore dei carichi per unità di superficie (KN/mq) calcoliamo il carico totale permanete (G), il carico totale accidentale (Q) come segue:

Questa esercitazione viene svolta con l’obiettivo di individuare il metodo di ripartizione di una forza orizzontale, come quella sismica e del vento, sui diversi telai che costituiscono una struttura, applicando il metodo delle rigidezze.

Si prende in considerazione un edificio generico ad un solo piano, in cui struttura è composta da telai piani che, oltre a trasmettere i carichi verticali alla fondazione, possono costituire dei controventi per le azioni orizzontali. In particolare, i telai piani che compongono tale struttura sono realizzati sul modello del telaio Shear-type. I telai Shear-Type sono un modello teorico che hanno la capacità di possedere travi infinitamente rigide, questo fa si che le estremità dei pilastri non possono ruotare. La rotazione impedita porta a deformare i pilastri stessi come travi doppiamente incastrate. In questo caso la deformata si avvicina alla deformata di una trave deformabile per solo taglio.

Nell’ impalcato in figura si individuano 7 telai, 3 paralleli all’asse x e quattro paralleli all’asse y.

• Telaio 1 verticale: pilastri 1-5-9
• Telaio 2 verticale: pilastri 2-6-10
• Telaio 3 verticale: pilastri 3-7
• Telaio 4 verticale: pilastri 4-8
• Telaio 1 orizzontale: pilastri 1-2-3-4
• Telaio 2 orizzontale: pilastri 5-6-7-8
• Telaio 3 orizzontale: pilastri 9-10

I controventi, che per il solaio rappresentano vincoli cedevoli elasticamente, possono essere schematizzati nel piano dell’impalcato come molle.

In tutta la struttura sono presenti due tipologie di pilastro, uno rettangolare di dimensioni 50x30 cm e uno quadrato di dimensioni 30x30 cm. Pertanto otterremo tre momenti di inerzia distinti (bh^³/12), due per il pilastro rettangolare, uno rispetto ad x e l’altro rispetto ad y, e uno per il pilastro quadrato.

I₁xy= bh³/12= 67.500 cm⁴     I₂x= bh³/12= 31.2500 cm⁴    I₂y= b³h/12= 11.2500 cm⁴

Tramite la tabella excel, dopo aver inserito tutti i valori trovati dei diversi momenti d’inerzia, calcoliamo la rigidezza traslante associata a tutti i controventi, inserendo per ognuno di essi l’inerzia dei pilastri che lo compongono. Si parla di telai Shear type, pertanto, per trovare la rigidezza traslante di un telaio composto da n pilastri utilizziamo la formula:

Si ottiene anche una tabella riassuntiva in cui vengono riportate le rigidezze di tutti i controventi calcolati precedentemente. Nella stessa tabella, si devono inserire le distanze di ogni controvento, calcolate da un’origine O arbitraria, che per comodità collochiamo nell’angolo in basso a sinistra dell’impalcato.

Si calcola ora il centro di massa dell’edificio, che corrisponde al centro delle aree dato che si considera l’impalcato con densità di massa uniforme, suddividendo la struttura in tre figure elementari di cui conosciamo il centro in modo intuitivo.

Per farlo utilizziamo la formula derivata da quella per ottenere le coordinate del centro di un sistema di vettori paralleli:

Giunti a questo punto, si calcola la rigidezza totale orizzontale, data dalla somma delle singole rigidezze dei controventi orizzontali, e la rigidezza totale verticale, data dalla somma delle singole rigidezze dei controventi verticali. Così sarà possibile calcolare il centro delle rigidezze riadattando la formula precedentemente utilizzata per il centro di massa, e la rigidezza torsionale totale.

Si riesce così ad individuare sia il centro di massa G sia il centro delle rigidezze C, dell’intero impalcato.

Si effettua l’analisi dei carichi sismici per ricavare la forza che agisce nel centro di massa. Si calcola il carico totale permanente (G) e accidentale (Q) del solaio, partendo dal valore dei carichi per unità di superficie [kN/mq] e utilizzando le seguenti formule:

G = (q_s + q_u) A_tot      Q = q_a A_tot

In accordo con la normativa tecnica si utilizza la combinazione sismica per calcolare i pesi sismici:

W = G + ψ_2j · Q   in cui ψ rappresenta il coefficiente di contemporaneità indicato dalla normativa.

F = W c    moltiplicando W, ossia il peso sismico, per un coefficiente di intensità sismica c che tiene conto della sismicità del luogo di progettazione dell’edificio, si ottiene F, la forza sismica da applicare al centro di massa.

Ora si considera l’azione della forza sismica lungo x e poi lungo y. Si trova lo spostamento orizzontale, verticale e la rotazione tramite le seguenti formule:

Ora che abbiamo tale forza la andiamo ad applicare nel centro d’area creando 2 casi:

• forza applicata in direzione x, che comporterà ad possibile rotazione e traslazione orizzontale dell’impalcato
• forza applicata in direzione y, che comporterà ad possibile rotazione e traslazione verticale dell’impalcato 
• 

In questa esercitazione si metteranno a confronto i comportamenti di differenti tipi di arco soggetti a un carico uniforme.

arco a tutto sesto   F = L

arco ribassato        F < L

arco parabolico     F > L

1_ Disegnare, su Autocad 3D o Rhino, i tre tipi di arco, tutti con la stessa luce e importarli in SAP con il formato .dxf

2_ Determinare il modello di arco a tre cerniere inserendo: ai punti d'imposta di ogni arco il vincolo cerniera esterna, mentre in chiave usare il comando Release/Partial Fixity per creare una cerniera interna, annullando il momento.

3_ Stabilire la sezione dell'arco, impostandolo come se fosse in cemento con una sezione rettangolare di 40x25cm, avendo la dimensione più grande perpendicolare alla linea dell'asse.

4_ Applicare un carico di 20KN/m su tutta la struttura, ricordando di selezionare l'opzione Gravity projected, affinchè il carico sia distribuito in maniera uniforme rispetto alla curvatura dell'arco.

5_ Analizzare i tre archi. Le reazioni vincolari alle imposte saranno per entrambi r_v = ql e r_o = ql²/2f

Più la freccia si avvicina all'imposta dell'arco, più la spinta aumenta, poiché sono inversamente proporzionali.

Si vuole calcolare la rigidezza di un impalcato costituito da sette telai di cemento armato basati sul modello teorico "shear-type", osservare la collocazione del suo centro delle rigidezze rispetto al centro di massa, e la sua capacità di rispondere alle sollecitazioni orizzontali (in particolar modo, quelle sismiche). L'impalcato è il seguente:

I pilastri sono tutti di sezione rettangolare 30x50 cm, alcuni disposti lungo x, altri lungo y, come si piò osservare dalla pianta, e la loro altezza è di 300 cm.

Nel primo step della tabella Excel, vengono richiesti i dati riguardanti la geometria e i materiali dei vari telai: l'altezza h, il modulo plastico E (da materiale, 21000 N/mmq) e i momenti d'inerzia I (per la sezione rettangolare bh³/12, quindi 312500 cm⁴ quello maggiore, 112500 cm⁴ quello minore).

La tabella è quindi in grado di  calcolare la rigidezza traslante di ogni telaio , che si ottiene dalla formula: 

Questo perché si assume il modello "shear-type", nel quale ogni pilastro ha una rigidezza pari a 12EI/h³.

Ogni telaio è in grado di opporsi a sforzi orizzontali paralleli al suo sviluppo (possiamo quindi rappresentare ogni telaio con una molla che ostacola gli spostamenti):

E' ora necessario calcolare le coordinate X e Y del centro di massa G, che si calcolano tenendo conto dei due centri G1 e G2 dei due rettangoli (si decide di far coincidere il centro di massa con quello d'area), ed inserendoli nella formula per il centro di un sistema di vettori paralleli:

Il centro di massa risulta quindi di coordinate (8,13 m ; 4,13 m)

Dopo aver trovato G, serve trovare anche il centro delle rigidezze C, con la stessa formula del centro del sistema di vettori paralleli, i cui dati vengono raccolti nella tabella dello step 2 di cui sopra:

Il centro delle rigidezze C risulta avere coordinate (9,08 m; 2,94 m). In seguito viene mostrata la reciproca posizione di G e C nell'impalcato:

Una buona progettazione impone che i due centri non abbiano una distanza troppo elevata, onde limitare (o addirittura, annullare) la rotazione rigida dell'impalcato, e di conseguenza momenti torcenti sui pilastri, sottoponendo la struttura a sola traslazione pura. In questo caso la distanza è accettabile, anche se l'impalcato tende comunque a ruotare: è necessario allora calcolare la sua rigidezza torsionale come mostrato nella tabella dello step 4 di cui sopra.

Il foglio Excel calcola quindi prima le distanze dei controventi dal centro delle rigidezze, in modo da poter applicare la formula seguente:

La rigidezza torsionale totale risulta quindi 7877467,28 KNm.

Lo step 5 riguarda il calcolo dell'entità del carico sismico dell'impalcato, per il quale è necessario conoscere i carichi strutturali qs, i carichi permanenti non strutturali qp ed i carichi accidentali qa: si considera un solaio in laterocemento (vedere esercitazioni 2 e 3 per dettagli) ad uso residenziale, ovvero:

qs=1,86 KN/mq, qp=1,91 KN/mq, qa=2 KN/mq.

Essi devono essere moltiplicati per l'area dell'edificio in modo da ottenere  i carichi totali G = 452,4 KN e Q = 240 KN, a loro volta sommati e moltiplicati per il coefficiente di contemporaneità 0,8 per avere il valore del peso sismico W = 644,4 KN; infine è necessario moltiplicare per il coefficiente d'intensità sismica c, che dipende dall'area geografica e dalla sua sismicità (in questo caso vale 0,1) fino ad ottenere lo sforzo sismico orizzontale F =64,44 KN.

Gli step 6 e 7 calcolano i valori degli spostamenti orizzontali e verticali e della rotazione dell'impalcato applicando la forza F sul centro di massa G, rispettivamente lungo l'asse X e lungo l'asse Y, con le formule qui riportate:

Il momento torcente M che appare nella formula ha come forza la forza sismica F e come braccio la distanza tra centro di massa e centro delle rigidezze, e vale quindi -61,34 KNm.

La tabella quindi calcola la forza sui singoli controventi (sempre una volta per Fx e una per Fy) e per fare ciò utilizza le seguenti formule nel caso della forza lungo X: 

rispettivamente per i controventi orizzontali e quelli verticali;  Lo stesso principio si applica con la forza lungo Y:

L’obiettivo di questa esercitazione è quello di calcolare come viene ripartita una forza orizzontale, in questo caso quella sismica, su diversi telai che compongono una struttura, applicando il  metodo delle rigidezze.

Prendiamo in considerazione un generico edificio ad un solo piano, la cui struttura è composta da telai piani che, se ben progettati, oltre a trasmettere i carichi verticali alla fondazione possono fungere da controventi per le azioni orizzontali.

In particolare, i telai piani che compongono la struttura sono di tipo Shear-type.

Nel presente impalcato si possono individuare otto telai, quattro paralleli all’asse x e e quattro paralleli all’asse y.

• Telaio 1 verticale: pilastri 1-4
• Telaio 2 verticale: pilastri 2-5-7-10
• Telaio 3 verticale: pilastri 3-6-8-11
• Telaio 4 verticale: pilastri 9-12
• Telaio 1 orizzontale: pilastri 1-2-3
• Telaio 2 orizzontale: pilastri 4-5-6
• Telaio 3 orizzontale: pilastri 7-8-9
• Telaio 4 orizzontale: pilastri 10-11-12

Complessivamente sono presenti due tipologie di pilastro, uno rettangolare di dimensioni 30x40 cm e uno quadrato di dimensioni 30x30 cm. Pertanto otterremo tre momenti di inerzia distinti (bh²/12), due per il pilastro rettangolare, a seconda se viene calcolato rispetto ad x o rispetto ad y, e uno per il pilastro quadrato.

I controventi, che per il solaio rappresentano vincoli cedevoli elasticamente, possono essere schematizzati nel piano dell’impalcato come molle.

STEP 1: tramite la tabella excel, calcoliamo la rigidezza traslante associata a tutti i controventi, inserendo per ognuno di essi l’inerzia dei pilastri che lo compongono. Stiamo parlando di telai Shear type, pertanto, per trovare la rigidezza traslante di un telaio composto da n pilastri utilizziamo la formula:

STEP 2: otteniamo una tabella riassuntiva in cui vengono riportate le rigidezze di tutti i controventi calcolati nel primo step. In più, nella stessa tabella, inseriamo le distanze di ogni controvento da un’origine O arbitraria, che per comodità collochiamo nell’angolo in basso a sinistra dell’impalcato.

STEP 3: a questo punto calcoliamo il centro di massa dell’edificio, che corrisponde al centro delle aree dato che consideriamo l’impalcato con densità di massa uniforme, suddividendo la struttura in tre figure elementari di cui conosciamo il centro in modo intuitivo.

Per farlo utilizziamo la formula derivata da quella per ottenere le coordinate del centro di un sistema di vettori paralleli:

STEP 4: calcoliamo la rigidezza totale orizzontale, data dalla somma delle singole rigidezze dei controventi orizzontali, e la rigidezza totale verticale, data dalla somma delle singole rigidezze dei controventi verticali.

In questo modo sarà possibile calcolare il centro delle rigidezze riadattando la formula precedentemente utilizzata per il centro di massa, e la rigidezza torsionale totale.

Si possono ora posizionare centro di massa e centro delle rigidezze all’interno del sistema di riferimento in cui abbiamo disegnato l’impalcato. Questa operazione ci consente di verificare se l’impalcato subisce una rotazione, infatti, dal momento che la forza orizzontale derivante dal sisma deve essere applicata sul centro di massa, l’unico caso in cui non abbiamo rotazione, ma solo traslazione verticale o orizzontale, è quello in cui centro di massa e centro delle rigidezze coincidono.

 Come evidente dall’immagine i due centri non coincidono, pertanto applicando la forza sismica nel centro di massa una volta lungo X e una volta lungo Y, otteniamo in entrambi i casi traslazione e rotazione.

STEP 5: effettuiamo l’analisi dei carichi sismici per ricavare la forza che agisce nel centro di massa. Ipotizziamo di avere un solaio in latero cemento e calcoliamo il carico totale permanente (G) e accidentale (Q) partendo dal valore dei carichi per unità di superficie [kN/mq], utilizzando le seguenti formule:

G = (q_s + q_u) A_tot      Q = q_a A_tot

In accordo con la normativa tecnica utilizziamo la combinazione sismica per calcolare i pesi sismici:

W = G + ψ_2j · Q   in cui ψ rappresenta il coefficiente di contemporaneità indicato dalla normativa.

F = W c    moltiplicando W, ossia il peso sismico, per un coefficiente di intensità sismica c che tiene conto della sismicità del luogo di progettazione dell’edificio, otteniamo F, la forza sismica da applicare al centro di massa.

STEP 6 e 7: consideriamo l’azione della forza sismica lungo x e poi lungo y e troviamo lo spostamento orizzontale, verticale e la rotazione tramite le seguenti formule:

Per ricavare la forza sui singoli controventi nei due casi di carico utilizziamo: