SdC(b) (LM PA)

INTRODUZIONE:

In questa esercitazione vedremo come si ripartisce una forza orizzontale (di natura sismica o atmosferica) sui telai che compongono la struttura intelaiata, che in questa esercitazione sarà di un solo piano.

Il sistema trave-pilastro permette, oltre che trasmettere i carichi verticali alle fondazioni, di sopportare le forze orizzontali rendendo i sistemi pilastro-trave dei controventi. La struttura esaminata sarà in cemento armato, e la tipologia dei controventi è chiamata telaio SHEAR-TYPE, che presenta tutti nodi all'incastro e la trave è ipotizzata infinitamente rigida a flessione rispetto ai pilastri, che vengono dotati di rigidezza k.

N.B.: Affinchè un sistema di controventamento sia efficace, gli impalcati vengono considerati corpi rigidi sul proprio piano (mentre al di fuori si inflettono) perciò i controventi reagiscono alla forza orizzontale che tende a spostarli, con la loro elasticità, ciò impone che un controvento, nel piano impalcato, sia un appoggio cedevole elasticamente.

Nella figura sopra è rappresentato un telaio shear-type a due ritti, dove la forza F sposta il traverso, che di conseguenza trascina con se i pilastri (si comportano come una trave doppiamente appoggiata). Il legame tra F e sigma (spostamento) è esplicitato nella formula F= [(12EI₁/h³) + (12EI₂/h³)]sigma (valevole per un telaio shear-type a due piedritti), dalla quale si ricava che k (rigidezza traslante di ogni pilastro)=12EI/h³,poichè F=k*sigma. Nel caso generale:

Grazie a questa esercitazione saremo in grado di determinare la reazione elastica di ogni controvento che sarà uguale ed opposta alla forza orizzontale che ogni singolo controvento è chiamato a ricevere attraverso il solaio (secondo il principio di azione-reazione).

DISEGNO:

Telai // all'asse y

Telaio 1v pilastri 1-5-9 ; Telaio 2v pilastri 2-6-10 ; Telaio 3v pilastri 3-7 ; Telaio 4v pilastri 4-8

Telai // all'asse x

Telaio 1o pilastri 1-2-3-4 ; Telaio 2o pilastri 5-6-7-8 ; Telaio 3o pilastri 9-10

Trattandosi di vincoli cedevoli elasticamente, i controventi vengono assimilati a molle.

DIMENSIONAMENTO:

Apro il file Excel, inserisco i dati di cui dispongo:

E=Modulo Elastico di Young (in Mpa o N/mm²); per cls con classe di resistenza C20/25

H=altezza dei pilastri (nel mio caso 3,5 m)

I=momento di inerzia di ciascun pilastro (calcolato lungo le due direzioni principali) che collabora alla formazione di ogni telaio.

Momento d'inerzia dei pilastri:

Pilastro m 0,5*0,3                     b=30 cm      h=50 cm       I_x= bh³/12 = 312500 cm4            I_y= hb³/12 = 112500 cm⁴                                                      

Inserisco i risultati nei calcoli e ottengo la rigidezza traslante dei miei 7 telai.

Nella seconda tabella riassumo le rigidezze dei controventi e inseriamo la distanza  dei rispettivi controventi dal punto di origine del sistema di riferimento da me adottato.

Nella terza tabella calcolo il centro di massa dell'impalcato, suddividendo l'area in forme geometriche  semplice delle quali mi ricaverò i singoli centri d'area.

Una volta trovate le coordinate rispetto a O dei singoli centri di massa, il file Excell mi calcola l'area totale dell'impalcato e il centro di massa totale grazie alle formule:

N.B. Le formule adottate si riferiscono ad un impalcato la quale densità sia omogenea su tutta l'area, trovandomi così sia il centro d'area che quello di massa, poichè coincidenti. Se la densità non fosse omogenea le formule adottate non sarebbero più valide.

Nella quarta tabella troviamo:

K_o=rigidezza totale orizzontale (somma delle rigidezze dei singoli controventi orizzontali)

K_v=rigidezza totale verticale (somma delle rigidezze dei singoli controventi verticali)

X_c e Y_c=coordinate dei centri di rigidezze dell'impalcato

K_phi=rigidezza torsionale totale.

Il centro delle rigidezze viene calcolato con la somma delle combinazioni tra le rigidezze e le rispettive distanze dal punto di origine. il tutto diviso per la rigidezza totale.

N.B.: La forza sismica deve essere applicata nel centro di massa G.

Dopodichè, posiziono i punti G e C (centro delle rigidezze) nello schema del mio impalcato, potendo così intuire se esso sarà soggetto solo a traslazione o anche a rotazione, ciò dipenderà dalla coincidenza o meno dei due punti.

In questo caso C e G non coincidono, anche se per poco, perciò in presenza di una forza orizzontale l'impalcato sarà soggetto sia a traslazione che a una rotzione, quest'ultima dovuta al braccio tra forza e centro delle rigidezze, creando un momento.

Con la quinta tabella effettuo l’analisi dei carichi sismici per ricavare la forza sismica che agisce nel centro di massa.

Riprendo i valori ottenuti nell'esercitazione per il dimensionamento della trave.

A partire da questi valori, il file calcola:

• G= il carico totale permanente, dato dal prodotto fra l’area totale e la somma dei carichi strutturali e permanenti
• Q= il carico totale accidentale, dato dal prodotta fra l’area totale e il carico accidentale
• W= Peso sismico o forza peso, calcolato attraverso la combinazione sismica, che richiede l’uso di ψ*²
• F= Forza sismica, data dal prodotta fra il peso sismico e c (coefficiente di intensità sismica in base alla localizzazione dell’edificio)

*² trattasi di un coefficiente di contemporaneità che tiene conto della funzione/categoria dell’impalcato; nel mio caso ho preso il valore riferito agli ambienti ad uso residenziale.

Le ultime due tabelle indicano come si ripartisce la forza sismica ai vari controventi, a seconda che essa agisca lungo l’asse x o l’asse y, e gli effetti cinematici (traslazione e rotazione rigida) sull’impalcato.

La sesta tabella ricava la forza sismica agente lungo X, la quale causa una traslazione orizzontale u ed una rotazione ϕ.

Il file di calcolo elabora i seguenti dati:

• M= momento torcente dato dalla formula F ^. (Y_c - Y_g)*³
• U_o= traslazione orizzontale dove u=F/ k_{o_tot}
• ϕ= rotazione cui è sottoposto l’impalcato; vale f= M/k_ϕ *⁴

*³ Nel mio caso è un valore positivo, quindi implica un momento antiorario.

*⁴ k_ϕ  è la rigidezza torsionale totale ricavata nella tabella 4.

La settima tabella ricava, invece, la forza sismica agente lungo Y, la quale, a sua volta, causa una traslazione verticale u ed una rotazione ϕ.

Nella tabella successiva, viene ripetuto lo stesso ragionamento, considerando la traslazione verticale:

• U_v= traslazione verticale dove u=F/ k_{v_tot}

Una volta determinati i valori dei gradi di libertà, posso ricavare la forza agente sui singoli controventi nei due casi di carico (verticale e orizzontale).

Noti u_{_o}, v_{_o}, ϕ, posso determinare le reazioni elastiche di ogni controvento attraverso le seguenti formule:

CASO 1 – Forza // all’asse X

• Fo_n=ko_n(u+ϕ∙ddo_n)       per i controventi orizzontali
• Fv_n=kv_n∙ϕ∙ddv_n            per i controventi verticali

CASO 2 – Forza // all’asse Y

• Fv_n=kv_n(v+ϕ∙ddv_n)       per i controventi verticali
• Fo_n=ko_n∙ϕ∙ddo_n            per i controventi orizzontali

Come già detto, si considera la forza nel piano dell’impalcato prima agente in direzione orizzontale e poi agente in direzione verticale; perciò analizziamo i due casi.

 

L’esercitaione prevede il dimensionamento di una travea sbalzo di un impalcato strutturale a telaio nella tre diverse teconologie: C.A., ACCIAIO E LEGNO.

Nella figura è rappresentato un impalcato strutturale 

Procedo con l’analisi dei carichi qs, qp , qa per ciascuna tecnologia:          

 

1) Dimensionamento di una trave a sbalzo in legno.

1.Sovraccarico strutturale qs

-travetto in legno: 2x (0,25*0,4)mq x 6KN/mc= 1,2 KN/mq

-tavolato: (0,03+*1*1)mq  x 6KN/mc = 0,18 KN/mq

Tot.  qs 1,38 KN/mq

2.Sovraccarico permanente qp

-piastrelle in ceramica: 0,01 x 0,2kN/mq = 0,002 KN/mq

-malta di allettamento: 0,02 x 20KN/mq = 0,4 KN/mq

-isolante: 0,04 x 1KN/mq = 0,04 KN/mq

-massetto: 0,08 x 18KN/mq = 1,44 KN/mq

 -Incidenza tramezzi 1 KN/mq  

 -incidenza impianti 0,5 KN/mq

 Tot. qp 3,382 KN/mq

3.Sovraccarico accidentale

 Da normativa per edifici a uso residenziale 2 KN/mq

4.Ora andiamo ad inserire i dati nella tabella excel  inserendo i qs, qp , qa e mi trovo il qu.                                     Inserisco la il valore della luce della trave per trovare quanto vale il Mmax.

5.Ho scelto il legno lamellare. Inserisco la tensione caratteristica a flessione fmk del legno che equivale a 24 MPa. La normativa mi fornisce la tensione di progetto fmd attraverso il coefficiente diminutivo dei valori di resistenza del materiale kmod = 0,80  ed il coefficiente parziale di sicurezza γm = 1,45 in base al materiale da me scelto. Trovo il valore della tensione di progetto fd.

6.Fisso la base b della trave per trovare hmin della sezione. Scelgo il valore di H che deve essere maggiore di hmin.

7.Dopo aver dimensionato la trave devo controllare l'abbassamento v_max e  verificare  che il rapporto tra la luce della mensola ed il suo spostamento sia  l/v_max >250 come imposto dalla normativa.

 

2) Dimensionamento di una trave a sbalzo in acciaio.

Visto che non era stato possibile pubblicare l'esercizitazione direttamente sul portale, si può trovare il file pdf con la presentazione in allegato.

L'esercitazione consiste nel dimensionamento delle travi a sbalzo di un solaio arbitrario.

Il dimensionamento delle travi è calcolato nelle tre differenti tipologie di solaio: Legno, Acciaio e Calcestruzzo armato.

L'altezza ammissibile della trave sollecitata sarà determinata come nell'esercitazione precedente, però successivamente sarà necessario effettuare la verifica a deformabilità, controllando l'abbassamento massimo dell'elemento strutturale in relazione alla sua luce.

Legno

1_Individuare nel solaio la trave a sbalzo più sollecitata e riferirsi ad essa per il dimensionamento. Nel caso ipotizzato l'interasse è di 4m, con una luce di 2,5m. Dunque ha un'area di influenza è di 10 m²

Analizzare i carichi che deve portare la struttura Qs, Qp, Qa, calcolare il momento massimo, tenendo in conto che lo schema strutturale di riferimento è quello della mensola. Nella sezione d'incastro si avrà il momento massimo che corrisponde a: M_max = qu x l²/2 = 76,11 KNm

Successivamente trovare l'altezza minima che sopporta la tensione di progetto e di conseguenza ingegnerizzarla, trovando così il profilo della trave 30cmx35cm

2_Effettuare la verifica a deformabilità della trave. Si controllerà che non vi siano spostamenti e deformazioni che possano compromettere l'efficienza della costruzione. Per questo i carichi che incidono sulla struttura sono calcolati seguendo la combinazione per gli stati limite di esercizio reversibili.

Qe = (qs + qp + 0,5qa) x 4 (interasse)= 14 kN/m

Per calcolare l'abbassamento massimo inserire nella tabella il modulo elastico E e il momento d'inerzia I_x

v_max = qe l⁴/ 8E I_x

Affinchè la sezione della trave sia verificata, il rapporto tra la luce della trave e il suo spostamento massimo deve essere maggiore di 250, come imposto dalla normativa in base al tipo di elemento strutturale considerato. L/v_max > 250

Acciaio

1_Individuare nel solaio la trave a sbalzo più sollecitata e riferirsi ad essa per il dimensionamento. Nel caso ipotizzato l'interasse è di 4m, con una luce di 2,5m. Dunque ha un'area di influenza è di 10 m²

Analizzare i carichi che deve portare la struttura Qs, Qp, Qa, calcolare il momento massimo, tenendo in conto che lo schema strutturale di riferimento è quello della mensola. Nella sezione d'incastro si avrà il momento massimo che corrisponde a: M_max =qu x l²/2 = 111,5 KNm

Successivamente trovare il modulo di resistenza a flessione minimo W_x che sopporta la tensione di progetto e di conseguenza ingegnerizzare la sezione, trovando così il profilo della trave IPE 300 con I_x 12,46 cm⁴ e peso proprio 0,422 KN/m.

2_Effettuare la verifica a deformabilità della trave. Si controllerà che non vi siano spostamenti e deformazioni che possano compromettere l'efficienza della costruzione. Per questo i carichi che incidono sulla struttura sono calcolati seguendo la combinazione per gli stati limite di esercizio reversibili.

Qe = (qs + qp + 0,5qa) x 4 (interasse) + peso trave = 21 kN/m

Nel caso dell'acciaio è stato aggiunto anche il peso proprio della trave, che a confronto con il legno ha un contributo significativo.

Per calcolare l'abbassamento massimo inserire nella tabella il modulo elastico E e il momento d'inerzia I_x

v_max = qe l⁴/ 8E I_x

Affinchè la sezione della trave sia verificata, il rapporto tra la luce della trave e il suo spostamento massimo deve essere maggiore di 250, come imposto dalla normativa in base al tipo di elemento strutturale considerato. L/v_max > 250

Calcestruzzo armato

1_Individuare nel solaio la trave a sbalzo più sollecitata e riferirsi ad essa per il dimensionamento. Nel caso ipotizzato l'interasse è di 4m, con una luce di 2,5m. Dunque ha un'area di influenza è di 10 m²

Analizzare i carichi che deve portare la struttura Qs, Qp, Qa, calcolare il momento massimo, tenendo in conto che lo schema strutturale di riferimento è quello della mensola. Nella sezione d'incastro si avrà il momento massimo che corrisponde a: M_max =qu x l²/2 = 139,16 Knm

Successivamente trovare l'altezza minima che sopporta la tensione di progetto e di conseguenza ingegnerizzarla, trovando così la sezione della trave 30cmx40cm che però dovrà essere verificata allo stato limite ultimo ovvero, considerando anche il suo peso proprio.

2_Dopo aver ottenuto la dimensione corretta della trave, effettuare la verifica a deformabilità. Si controllerà che non vi siano spostamenti e deformazioni che possano compromettere l'efficienza della costruzione. Per questo i carichi che incidono sulla struttura sono calcolati seguendo la combinazione per gli stati limite di esercizio reversibili.

Qe = (qs + qp + 0,5qa) x 4 (interasse) + peso trave = 30,3 KN/m

Per calcolare l'abbassamento massimo inserire nella tabella il modulo elastico E e il momento d'inerzia I_x

v_max = qe l⁴/ 8E I_x

Affinchè la sezione della trave sia verificata, il rapporto tra la luce della trave e il suo spostamento massimo deve essere maggiore di 250, come imposto dalla normativa in base al tipo di elemento strutturale considerato. L/v_max > 250

 

 

 

Il procedimento che segue descrive il calcolo relativo alla ripartizione delle forze orizzontali (sisma, vento…) sui telai che compongono la struttura rappresentata si seguito, attraverso il metodo delle rigidezze.

 

---

 

Si identificano nell’impalcato tutti i telai che fungono da controventi per le forze orizzontali che agiscono sulla struttura, quindi:

 

v1 - pilastri: 1-5-7

v2 - pilastri: 2-6-8

v3 - pilastri: 3-9

v4 - pilastri: 4-10

 

o1 - pilastri: 1-2-3-4

o2 - pilastri: 5-6

o3 - pilastri: 7-8-9-10

 

questi possono essere rappresentati come “molle”, e costituiscono i vincoli cedevoli elasticamente dell’impalcato:

Ipotizzando che il solaio, rappresentato successivamente, sia rigido a sufficienza da considerare la struttura composta da telai Shear-Type, possiamo calcolare la rigidezza traslante K_T di ogni telaio, ovvero la somma delle rigidezze dei singoli pilastri che lo compongono, la quale come sappiamo dipende dal modulo di Young E, dal Momento d’Inerzia I e dalla luce L (nello specifico l’altezza h).

poiché il telaio Shear-Type ha una rigidezza pari a:

meglio sintetizzata nell’immagine qui sotto:

Step-1: Con la formula della rigidezza vista prima possiamo calcolarla per tutti i telai orizzontali e verticali identificati, definendo:

E = 21000 N/mm²

H = 4mt

Ix = bh³/12 *

Iy = b³h/12 *

 

*rappresentazione della sezione rettangolare scelta per i pilastri dei telai Shear-Type

 

 

Step-2: Si riportano in tabella tutte le rigidezze calcolate nello step-1, con relative distanze tra esse e l’origine degli assi posto in basso a sinistra dell’impalcato:

La tabella riassuntiva riportata qui sopra servirà poi per velocizzare i calcoli del centro di rigidezza che viene calcolato nello step-3

 

 

Step-3: Per capire dove applicare la forza orizzontale, che servirà per i calcoli successivi, si ricava il centro di massa dell’impalcato dal procedimento che segue:

Così procedendo si ricavano le coordinate xG e yG che descrivono il centro di massa, ipotizzando che questo abbia la stessa densità per tutta la sua estensione, si ricava ponendo come la massa l’area della parte di impalcato in esame, poiché a parità di densità di tutto l’impalcato, il centro di massa coincide con il centro d’area.

Il procedimento è sintetizzato nella tabella sottostante che evidenzia un'unica area poiché essendo questo un impalcato “semplice” non vi è l’esigenza di dividerlo in parti:

 

 

 

Nell’immagine qui sopra è riportato l’impalcato con i due punti del centro di massa e del centro di rigidezza con le quote della loro distanza.

Non coincidendo questi due punti, nel momento in cui si applica una forza orizzontale (nel centro di massa dell’impalcato) si produrrà uno spostamento sull’asse in cui è applicata la forza ed un momento che farà ruotare l’impalcato con perno nel centro delle rigidezze e braccio pari alla coordinata che informa sulla distanza di questa forza dal centro delle rigidezze.

Qualora questi due punti coincidessero allora non vi sarà alcun momento ma solo spostamento.

 

Step-5: Nella seconda parte della tabella esposta prima, che si riporta di seguito, viene calcolata “Kφ” la rigidezza torsionale che si ricava tramite la sommatoria di tutte le rigidezze ricavate nello step-1 per la loro distanza dal centro delle rigidezze, ricavato nello step-4.

Questa rigidezza torsionale “Kφ” verrà utilizzato in seguito per il calcolo della rotazione dell’impalcato secondo una direzione:

 

Step-5: Per analizzare la ripartizione delle forze orizzontali, manca ora solo il carico orizzontale, essendo questo ipotizzabile come una forza sismica, si ricava tale carico dalle operazioni che seguono:

 

 

Nella tabella qui sopra sono riportati i carichi qs, qp e qa che equivalgono ai valori del solaio in figura e dei carichi accidentali attribuiti a residenza:

 

Si ricavano i carichi G e Q, in accordo con le norme tecniche vigenti, dalle seguenti formule:

Si distinguono due carichi differenti per il calcolo dei carichi sismici W poiché il carico G presenta tutti i carichi “permanenti” legati ad elementi strutturali e non, mentre il carico Q racchiude tutti i carichi accidentali che vengono compresi nella combinazione sismica ridotti di un coefficiente di contemporaneità ψ.

*Il valore di ψ è tabellato in normativa.

Questo carico W rappresenta la forza peso dell’edificio, espresso dalla massa dell’edificio per l’accelerazione di gravità.

Poiché il sisma ha un’accelerazione poco più piccola di quella di gravità, può essere introdotto un coefficiente riduttivo calcolato secondo la sismicità del luogo in cui si progetta la struttura:

Step-6: Si dovrà ora quantificare la ripartizione della forza sismica F lungo l’asse x e lungo quello y e, nello specifico, per ognuno dei controventi. Si ricorda che nel momento in cui la forza agente abbia un asse differente da quello del centro delle rigidezze (come nel caso dell’impalcato in questione), il corpo non si limita a traslare, ma ha anche una rotazione. Per poter conoscere il valore di questa rotazione, si calcola il Momento Torcente M per l’asse x, moltiplicando la forza sismica F per il suo braccio, ovvero la differenza tra l’ordinata del centro delle rigidezze e quella del centro di massa, e per l’asse y, utilizzando come braccio la differenza tra le ascisse dei due centri. Poi, si calcola la traslazione orizzontale, dividendo F per la rigidezza traslante orizzontale, la traslazione verticale, dividendo F stavolta per la rigidezza traslante verticale, e le rotazioni, dividendo i rispettivi Momenti Torcenti per la rigidezza rotazionale “Kφ”:

---

Questa esercitazione consiste nel calcolare come viene riparita una forza orizzontale (data dal vento o dal sisma) in un implacato. Vedremo quindi anche la modalità con il quale colare il centro d’area ed il centro delle rigidezze.

 L’impalcato analizzato è di un generico edificio di un solo piano costituito da telai piani in cls armato con tipologia di controventi modello shear-type : i telai Shear-Type sono un modello teorico che hanno la capacità di possedere travi infinitamente rigide, questo fa si che le estremità dei pilastri non possono ruotare. La rotazione impedita porta a deformare i pilastri stessi come travi doppiamente incastrate. In questo caso la deformata si avvicina alla deformata di una trave deformabile per solo taglio.

Poniamo l’impalcato in un piano cartesiano che ha come origine il punto più in basso a sinistra ed notiamo l’esistenza di 3 telai verticali, ovvero paralleli all’asse y, e 4 orizzontali, cioè paralleli allesse x :

Telaio 1v composto da: Pilastri 1, 4, 6, 9

Telaio 2v composto da: Pilastri 2, 5, 7

Telaio 3v composto da: Pilastri 3, 8, 10

Telaio 1o composto da: Pilastri 1, 2, 3

Telaio 2o composto da: Pilastri 4, 5

Telaio 3o composto da: Pilastri 6, 7, 8

Telaio 4o composto da: Pilastri 9, 10

 

I controventi saranno rappresentati come molle, aventi la loro adeguata rigidezza, essendo possibili vincoli cedevoli elasticamente dell’impalcato.

Procedo con il calcolarmi le rigidezze traslanti dei vari controventi. Essendo un modello shear type la rigidezze si ricaverà con:

 

F = (12EI₁ / h₃ + 12EI₂ / h₃) δ

F = k δ

k = 12EI₁ / h₃ + 12EI₂ / h₃

 

 

Generalizzando la formula da 2 ad n pilastri :

Dove E è il modulo elastico del cls armato (21000 MPa) ed I è il momentro d’inerzia che può essere, a seconda di come è disposto il pilastro:

I_x = bh³ / 12

I_y = b³h / 12

Una volta trovate le rigidezze traslanti dei telai procediamo calcolandoci le loro distanze dal punto di origine O.

Andiamo ora a calcolare e trovare il centro d’area dell’edificio. Nel nostro caso l’impalcato è un semplice rettangolo quindi il centro d’area si troverà esattamente all’incrocio delle 2 bisettrici.

Se la forma fosse stata complessa si proceva con il suddividere l’area totale in aree semplici trovando i centri di area di ognuna di esse (che equivarrà al centro geomentrico), successivamente di dovranno applicare 2 formule per trovare i 2 assi che si incontrano nel centro d’area :

x_G = ΣA_i x_Gi / A_tot

y_G = ΣA_i y_Gi / A_tot

Procediamo ora con il calcolarci la rigidezza totale orizzontale, rigidezza totale verticale, rigidezza torsionale ed il centro delle rigidezze individuato anch’esso da 2 assi cartesiani di grazie alle formule:

x_C = Σk_vi d_vi / k_{v_tot}

y_C = Σk_oi d_oi / k_{o_tot}

Calcolandoci tutte le distanze dei controventi dell’impalcato dal centro delle rigidezze C possiamo trovare il valore della rigidezza torsionale dato dalla formula:

kφ = Σk_vi dd²_vi+Σk_oi dd²_oi

Vediamo dove sono posizionati i due centri nell’impalcato:

Notiamo che il centro delle rigidezze è situtato molto in altro rispetto l’asse y ed è quindi abbastanza distante dal centro d’area, questo è dato per un irrigidimento eccessivo nella parte alta. Sapendo che la forza sismica che andremo a trovare verrà applicata nel centro d’area G vorrà dire che questa non coincidenza tra G e C provocherà delle rotazioni dell’impalcato.

Andiamo adesso a trovarci la forza sismica da applicare in G. Dobbiamo prima di tutto difinire i tre carichi distribuiti (q_s , q_p e q_a )in modo da calcolarci il carico totale permanente G_k ed il carico permanente accidentale Q_k :

G_k = (q_s + q_p ) A_tot

Q_k = q_a A_tot

Da normativa utilizziamo la combinazione sismica per calcolare i pesi sismici:

W = G_k + ψ_2j Q_k

Dove ψ _2j è il coefficiente di contemporaneità tabellato nella normativa.

Il peso sismico W rappresenta la forza peso dell’edificio, ovvero il rapporto tra massa ed accelerazione gravitazionale. Essendo l’accelerazione del sisma, però, minore dell’accelarazione gravitazionale, viene introdotto un coefficiente d’intensità sismica c che dipende dalla zona dove è collocato l’edificio. In questo modo possiamo trovarci la forza sismica:

F = c W

Ora che abbiamo tale forza la andiamo ad applicare nel centro d’area creando 2 casi:

• forza applicata in direzione x, che comporterà ad possibile rotazione e traslazione orizzontale dell’impalcato
• forza applicata in direzione y, che comporterà ad possibile rotazione e traslazione verticale dell’impalcato

Lo spostamento orizzontale, che chiamiamo u, è pari a:

u = F / k_{o_tot}

Lo spostamento verticale, che chiamiamo v, è uguale a:

v = F / k_{v_tot}

La rotazione φ impressa all’impalcato si trova con la seguente formula:

φ = M_c / kφ

Dove M_c è il momentro torcente dato dal rapporto tra forsa simica F per il braccio, ovvero la distanza tra G e C.

Possiamo infine ricavarci la forza sui singoli controventinei due casi di carico.

Quando la forza sarà applicata in direzione x, la reazione elastica dei controventi orizzontali sarà pari a:

F_{o_n} = k_{o_n} (u + φ dd_{o_n})

Mentre nei vericali sarà :

F_{v_n} = k_{v_n} φ dd_{v_n}

Quando la forza sarà applicata in direzione y, la reazione elastica dei controventi verticali sarà pari a:

F_{v_n} = k_{v_n} (v + φ dd_{v_n})

Mentre negli orizzontali sarà :

F_{o_n} = k_{o_n} φ dd_{o_n}

 

lo abbiamo risolto in aula.. ma non lo abiamo completato.. in allegato il risultato..

L'esercitazione consiste nel dimensionamento delle travi di un solaio arbitrario.

Il dimensionamento delle travi del solaio è calcolato nelle tre differenti tipologie di solaio: Legno, Acciaio e Calcestruzzo armato.

L'altezza ammissibile della trave sollecitata sarà determinata attraverso l'utilizzo di un foglio di calcolo, dove i dati inseriti saranno differenti a seconda della tipologia analizzata.

LEGNO

1_Individuare nel solaio la trave più sollecitata e riferirsi ad essa per il dimensionamento delle travi. Nel caso ipotizzato l'interasse è di 4m, con una luce di 5m. Dunque la trave che deve sopportare il maggior carico ha un'area di influenza è di 20 m²          

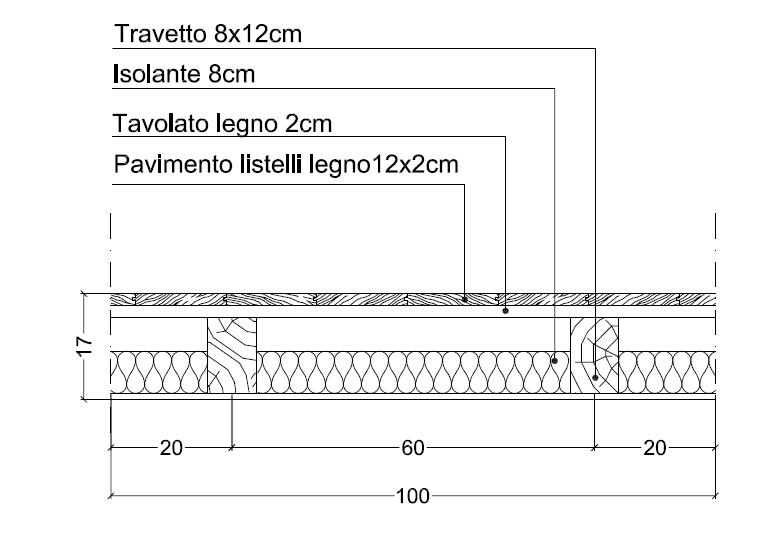
2_Si analizzano i carichi che sopporta la struttura. Si distinguono tre diversi tipi di carico:

Qs (KN/m²) CARICO STRUTTURALE dato dal peso proprio di tutti gli elementi costruttivi con funzione portante.

Qp (KN/m²) CARICO PERMANENTE dato da tutti gli oggetti tecnologici che non svolgono una funzione portante, ma che fanno parte permanentemente del telaio strutturale. A questi si aggiunge il carico dato dai tramezzi pari a 1KN/m² e quello dato dagli impianti 0,5 KN/m²

Qa (KN/m²) CARICO ACCIDENTALE dato dalla normativa in base alla destinazione d’uso dell'edificio.                  

CARICO STRUTTURALE (Qs)

In questa categoria per ora non è possibile inserire la trave principale perché ancora le sue dimensioni sono incognite, ma si calcola il peso dei travetti in legno di conifera.

Si hanno due travetti a m²

Peso specifico legno = 5 kN/m³
Volume totale = (0,08 m x 0,12 m x 1 m) x 2 = 0,0192 m³
qs = Volume totale x Peso specifico = 0,0192 m³ x 5 kN/m³ = 0,096 kN/m²
qs = 0,096 kN/m²

CARICO PERMANENTE (Qp)

qp = elementi del solaio + tramezzi + impianti

Isolante fibra di legno: qp₁ = 0,08 x 0,18 = 0,0144 kN/m²

Tavolato conifere: qp₂ = 0,02 x 5 = 0,1 kN/m²

Pavimento listelli legno wengè: qp₃ = 0,02 x 8,4 = 0,168 kN/m²

Incidenza Tramezzi: qp₄ = 1,5 kN/m²

Incidenza Impianti: qp₅ = 0,5 kN/m²

qp = 0,0144 + 0,1 + 0,168 + 1,5 + 0,5 = 2,28 kN/m²

CARICO ACCIDENTALE (Qa)

Il carico accidentale è quello che dipende dalla destinazione d’uso dell’edificio, si ipotizza una struttura adibita a civile abitazione, dunque secondo la normativa si applica:
qa = 2,0 kN/m²

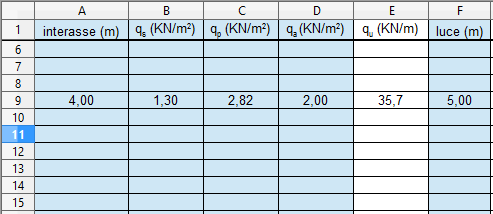
3_Sul foglio di calcolo Excel inserire i dati di progetto (interasse e luce) e i carichi precedentemente calcolati. Si otterrà il carico totale che subisce la trave, dunque distributo sull'area d'influenza:              qu = (1,3qs + 1,3qp + 1,5qa) x 4 (interasse)= 24,35 kN/m

I carichi sono stati moltiplicati con dei coefficienti di sicurezza.

Inoltre viene calcolato il momento massimo M_max = qu x l²/8 = 76,11 KNm

4_Scegliere il legname della trave: legno lamellare GL 24h che ha una resistenza caratteristica a flessione fmk di 24 N/mm² . Il valore kmod = 0,8 dipende dalla classe d’uso della trave, è un coefficiente correttivo dei valori di resistenza del materiale considerando l'aggravio delle condizioni esterne d'esercizio come particolari condizioni di carico e umidità. Il coefficiente parziale di sicurezza γm = 1,45.

Si ottiene la tensione ammissibile di progetto fmd = kmod x fmk /γm = 13,24 N/mm²

 

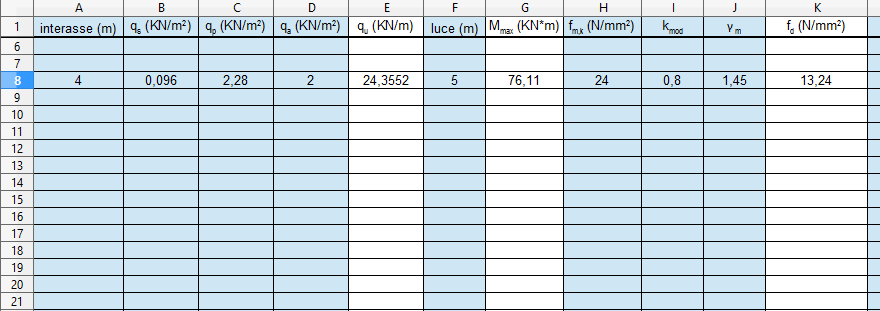
5_Per dimensionare la trave, fissare una dimensione, 30 cm di base così da ottenere l’altezza minima che serve alla trave per resistere alla tensione di progetto.

L’altezza calcolata H_min = √6 M_max / fmd x b

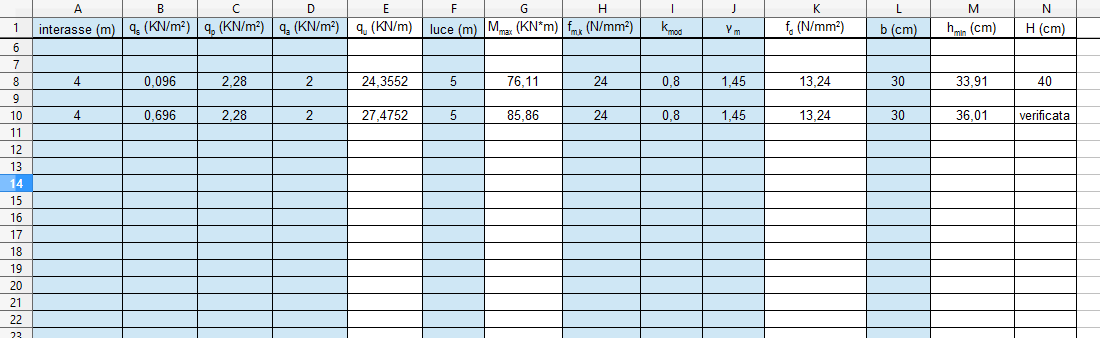
deve essere ingegnerizzata, ovvero adattata ai profili tabellati, dunque si sceglierà un'altezza sovradimensionata che consideri anche l'effetto finale del peso proprio della trave, inizialmente non considerato. Profilo 30cmx40cm H

6_Per concludere verificare che inserendo anche il peso prioprio della trave scelta la tensione di verifica sarà minore della tensione ammissibile. Il carico qs cambierà in qs = q travetti + q trave

qs trave = (0,3 x 0,4 x 1) x 5 = 0,6 kN/m²

qs = 0,096 + 0,6 = 0,696 kN/m²

Cambiando i dati nel foglio Excel si vede come l'altezza minima è cambiata ma non ha superato l'altezza scelta nel dimensionamento della trave: è verificata.

ACCIAIO

1_Per l’acciaio come per il legno si utilizza una tecnologia costruttiva coerente con il tipo di materiale. Individuare nel solaio la trave più sollecitata e riferirsi ad essa per il dimensionamento delle travi. Area di influenza 4m x 5m = 20 m²

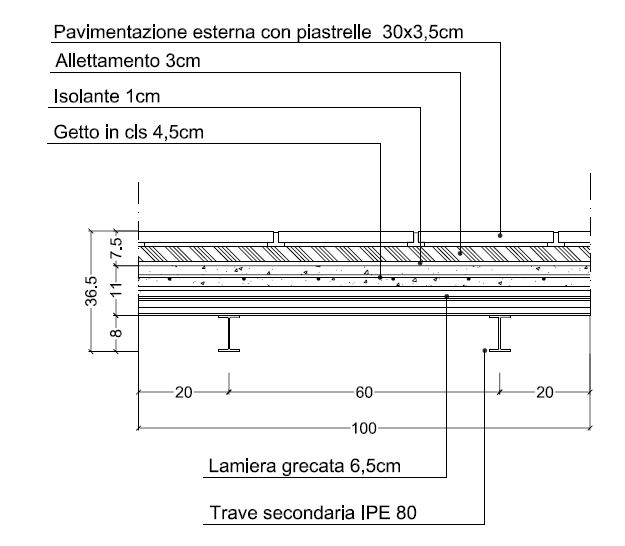
2_Si analizzano i carichi che sopporta la struttura. Si distinguono tre diversi tipi di carico:

CARICO STRUTTURALE (Qs)

Esattamente come per il legno questo solaio è a doppia orditura, però nel carico strutturale ora si inserisce solo l'orditura secondaria, in quanto la principale è incognita.

Si hanno due travetti IPE 80 a m²

Travetti: Peso specifico= 78,5 kN/m³
Volume totale = (7,64 cm² X 100 cm) x 2 = 1528 cm³
qs₁ = Volume totale x Peso specifico = 0,001528 m³ x 78,5 kN/m³ = 0,12 kN/m²

Lamiera grecata: qs₂ = 0,0785 kN/m²

Il valore del peso della lamiera viene fornito direttamente dal produttore su unità di superficie.

Getto di completamento in calcestruzzo armato: peso specifico = 25 kN/m²

Volume = (4,5 cm x 100 cm) x 100 cm = 45000 cm³ = 0,045 m³

qs₃ = Volume totale x Peso specifico = 0,045 x 25 = 1,125 kN/m²

qs = 0,12 + 0,0785 + 1,08 = 1,3 kN/m ²

CARICO PERMANENTE (Qp)

qp = elementi del solaio + tramezzi + impianti

Termofonoisolante a base polipropilene: qp₁ = 0,002 kN/m²

Massetto di allettamento: qp₂ = 0,03 x 18 = 0,54 kN/m²

Pavimento in gres porcellanato: qp₃ = 0,035 x 8 = 0,28 kN/m²

Incidenza Tramezzi: qp₄ = 1,5 kN/m²

Incidenza Impianti: qp₅ = 0,5 kN/m²

qp = 0,002+ 0,54 + 0,28 + 1,5 + 0,5 = 2,822 kN/m ²

CARICO ACCIDENTALE (Qa)

Il carico accidentale è quello che dipende dalla destinazione d’uso dell’edificio, si ipotizza una struttura adibita a civile abitazione, dunque secondo la normativa si applica:
qa = 2,0 kN/m ²

3_Sul foglio di calcolo Excel inserire i dati di progetto (interasse e luce) e i carichi precedentemente calcolati. Si otterrà il carico totale che subisce la trave, dunque distributo sull'area d'influenza:

qu = (1,3qs + 1,5qp + 1,5qa) x 4 (interasse) = 35,7 kN/m

I carichi sono stati moltiplicati con dei coefficienti di sicurezza.

Inoltre viene calcolato il momento massimo M_max = qu x l²/8 = 111,5 KNm

4_Scegliere la classe di acciaio per definire quale è la tensione ammissibile. Classe Fe360/S2735 con tensione caratteristica di snervamento fyk = 235 MPa.

Si trova così la tensione di progetto fd = fyk /γs = 235/1,15 = 223,81 N/mm ²

dove γs = 1,15 coefficiente parziale di sicurezza dell'acciaio.

Ricavare dal foglio di calcolo il modulo di resistenza a flessione minimo rispetto all'asse x.

W_x,min = M_max / fd = 498,36 cm³

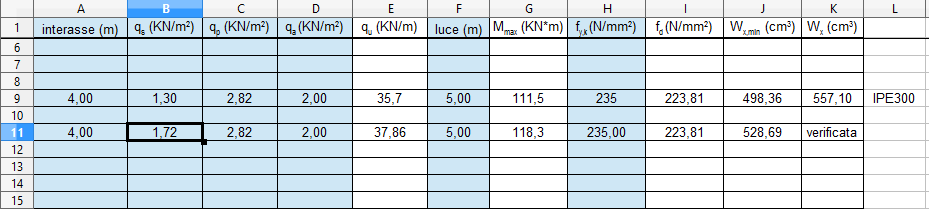
5_Considerando W_x,min trovare nella tabella dei profilati metallici un profilato con W_x > W_x,min

IPE 300 con W_x = 557,1 cm³

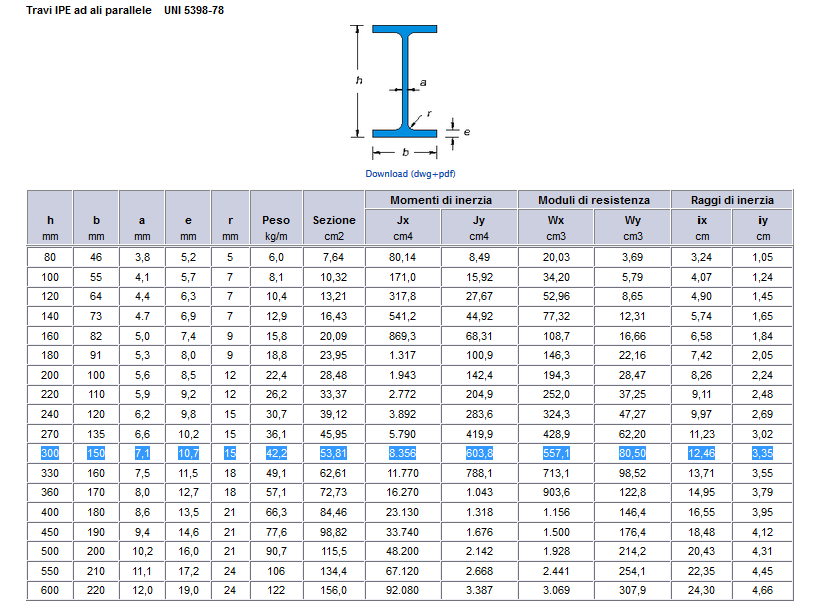
6_Per concludere verificare che il profilo scelto come trave principale riesca a sostenere anche il peso proprio. Il carico qs cambierà:

qs trave = 0,005381 m³ x 78,5 KN/m³ = 0,42 kN/m²

qs = 1,3+ 0,42 = 1,72 kN/m ²

Cambiando i dati nel foglio Excel si vede come la resistenza minima a flessione è cambiata, ma non ha superato quella della trave scelta: è verificata.

CALCESTRUZZO ARMATO

1_Analizzare anche qui il carico per la relativa area d'influenza della trave maggiormente sollecitata. Area di influenza 4m x 5m = 20 m²

Si distinguono tre diversi tipi di carico:

CARICO STRUTTURALE (Qs)

La parte struttura di questo solaio corrisponde al getto in calcestruzzo armato che viene colato tra gli elementi di alleggerimento.

Travetti cls: Peso specifico= 25 kN/m³

Due travetti a m²
Volume totale = (0,1 m X 0,18 m x 1m) x 2 = 0,036 m³
qs₁ = Volume totale x Peso specifico = 0,036 m³ x 25 kN/m³ = 0,9 kN/m²

Pignatte: Peso specifico= 8 kN/m³

Due pignatte a m²

Volume totale = (0,18 m X 0,4 m x 1m) x 2 = 0,144 m³

qs₂ = 0,144 m³ x 8 kN/m³ = 1,152 kN/m²

Getto di completamento in calcestruzzo armato: peso specifico = 24 kN/m²

qs₂ = 0,04 m³ x 24 kN/m³ = 0,96 kN/m²

qs = 0,9 + 1,152 + 0,96 = 3,012 kN/m ²

CARICO PERMANENTE (Qp)

qp = elementi del solaio + tramezzi + impianti

Termofonoisolante a base polipropilene: qp₁ = 0,002 kN/m²

Massetto di allettamento: qp₂ = 0,03 x 18 = 0,54 kN/m²

Pavimento in gres porcellanato: qp₃ = 0,035 x 8 = 0,28 kN/m²

Incidenza Tramezzi: qp₄ = 1,5 kN/m²

Incidenza Impianti: qp₅ = 0,5 kN/m²

qp = 0,002+ 0,54 + 0,28 + 1,5 + 0,5 = 2,822 kN/m ²

CARICO ACCIDENTALE (Qa)

Il carico accidentale è quello che dipende dalla destinazione d’uso dell’edificio, si ipotizza una struttura adibita a civile abitazione, dunque secondo la normativa si applica:
qa = 2,0 kN/m ²

2_Sul foglio di calcolo Excel inserire i dati di progetto (interasse e luce) e i carichi precedentemente calcolati. Si otterrà il carico totale che subisce la trave, dunque distributo sull'area d'influenza:

qu = (1,3qs + 1,5qp + 1,5qa) x 4 (interasse) = 44,6 kN/m

I carichi sono stati moltiplicati con dei coefficienti di sicurezza.

Inoltre viene calcolato il momento massimo M_max = qu x l²/8 = 139,4 Knm

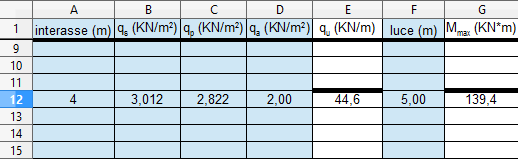
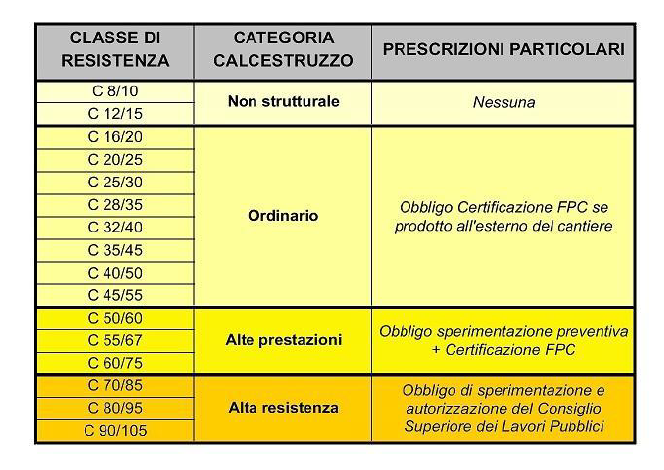
3_Visto che il calcestruzzo armato è un materiale non omogeneo, composto da calcestruzzo e da acciaio occorre scegliere le classi di resistenza del calcestruzzo e dei tondini d'acciaio. Per il calcestruzzo si può optare per uno C32/40 con una resistenza a compressione di 40 MPa (N/mm²).

La scelta dell’acciaio è condizionata dalla normativa, in questo caso viene scelto il B450C con 450 MPa di limite di snervamento. Inserendo questi dati nelle caselle apposite si trovano due valori fyd e fcd.

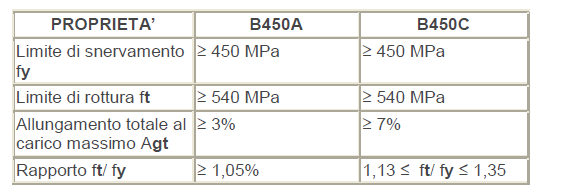
La tensione di progetto dell'acciaio fyd = fyk /γs = 450/1,15 = 391,3 N/mm ² e la tensione di progetto del calcestruzzo compresso fcd = α_cc fck /γc = 22,67 N/mm² servendosi del coefficiente riduttivo per le resistenze di lunga durata α_cc = 0,85 e del coefficiente parziale di sicurezza del calcestruzzo γc = 1,5.

4_Dai valori delle tensioni di progetto si determina l'altezza utile della sezione, scegliendo sempre come dato di partenza la base, b = 30cm. h_u = r √M_max /b = 32,3 cm

L'altezza minima da prendere in considerazione per il dimensionamento sarà H_min = h_u + δ = 37,3 cm ovvero l'altezza utile più la distanza tra il baricentro dell'armatura e il filo del calcestruzzo treso, copriferro di 5cm.

5_Anche nel caso del calcestruzzo armato le sezioni devono essere ingegnerizzate, portando l'altezza alla decina immediatamente superiore al valore minimo. H = 40cm

6_Per concludere verificare che il profilo scelto come trave principale riesca a sostenere anche il peso proprio. Il carico qu cambierà, poiché sarà aggiunto il peso proprio della trave (0,12 m³ x 25 KN/m³ = 3 kN/m²⁾ moltiplicato per il fattore di sicurezza 1,3.

Se l'altezza minima risultante dal nuovo dimensionamento è minore di quella imposta precedentemente come altezza della trave, la sezione risulterà verificata anche con l'aggiunta del suo peso proprio.

Nel caso delle travi in calcestruzzo armato questa verifica è molto importante in confronto al legno o all'acciaio, proprio perchè il suo peso proprio porta ad un incremento importante del momento flettente, e dunque della tensione ammissibile.