Blog

Introduzione

Il metodo delle rigidezze è un metodo per risolvere strutture iperstatiche ed in particolare abbiamo studiato tale metodo per calcolare portali, telai, telai shear type e travi Virendeel.

Come sappiamo la rigidezza è la forza necessaria a produrre uno spostamento unitario. 

Per questa esercitazione vogliamo applicare il metodo delle rigidezze ad una trave Virendeel.

Step_1: Deformata 

Conoscendo la deformata di una trave incastro-incastro con cedimento strutturale, o il comportamento deformativo di un telaio shear type possiamo facilmente dedurre la deformata di una Virendeel.

Essendo una trave Virendeel una sovrapposizione di telai shear type possiamo disegnare la deformata.

Step_ 2: Calcolo Taglio e Momento nelle travi

Dallo studio dello shear type sappiamo che il taglio si ripartisce in maniera proporzionale alla rigidezza e alla luce. Perciò ogni pilastro contrasterà metà del carico. 

_Tp1= F/2 

T_p2= F 

_Tp3= 3F/2

_Tp4= 2F 

_Tp5= 5F/2 

_Tp6= 3F 

Per il calcolo del momento agli incastri basterà moltiplicare il taglio per metà della luce:

M_p1= F/2 * L/2 = FL/4

 M_p2= F * L/2 = FL/2

M_p3= 3F/2 * L/2 = 3FL/4

M_p4= 2F * L/2 = FL

M_p5= 5F/2 * L/2 = 5FL/4

M_p6= 3F * L/2 = 3FL/2

Step_3: Equilibrio al nodo di incastro

Per verificare il comportamento delle travi infinitamente rigide dobbiamo innanzitutto verificare l'equilibrio ai nodi.

Step_4: Momento nella Trave

Ora possiamo facilmente disegnare il diagramma dei momenti sulle travi.

Step_5: Taglio della Trave

Essendo il momento della trave lineare, avremo un taglio costante che sarà dato dalla somma dei momenti ai bordi diviso la luce della trave.

T_t1 = (FL/4 + FL/4)/H = FL/2H

T_t2= (3FL/4 + 3FL/4)/H = 3FL/2H

T_t3= (5FL/4 + 5FL/4)/H = 5FL/2H

T_t4= (7FL/4 + 7FL/4)/H = 7FL/2H

T_t5= (9FL/4 + 9FL/4)/H = 9FL/2H

T_t6= (11FL/4 + 11FL/4)/H = 11FL/H

Step_6: Verifica su SAP

Per la verifica su SAP costruisco un "2D Frames" con la stessa geometria di cui sopra.

Per simulare la rigidezza infinita bisogna impostare un materiale che abbia o altezza infinita o modulo di elasticità infinito.

DEFINE-FRAME-FRAME SECTION-ADD NEW PROPERTY-NEW MATERIAL 

Importante: in LOAD PATTERN ricordarsi di mettere al carico DEAD il SELF MULTIPLIE WEIGHT pari a O.

A questo punto possiamo far partire l'analisi (RUN NOW)

Introduzione

Il metodo delle Forze è uno dei metodi per risolvere i sistemi strutturali iperstatici.

Ricordiamo che una struttura si dice iperstatica quando i gradi di vincolo sono maggiori dei gradi di libertà. In questo caso le equazioni di equilibrio non sono sufficienti per determinare le reazioni vincolari. Perciò se ci basiamo esclusivamente sulle equazioni cardinali della statica, i sistemi di travi iperstatici sono equilibrati da infinite soluzioni di reazioni vincolari.

Quindi tra le infinite soluzioni di equilibrio statico dovrò scegliere quella che, oltre l’equilibrio, implichi anche la congruenza, ovvero il rispetto dei vincoli esterni ed interni iperstatici nonostante le deformazioni indotte nella struttura dai carichi esterni.

Step_1: Verifica Iperstaticità della Trave

La trave presa in considerazione ha 3 gradi di libertà e 6 gradi di vincolo e quindi è 3 volte iperstatica. 

Step_2: Scegliere la struttura isostatica di riferimento

Introducendo 3 momenti in B,C e in D  e separando la struttura otteniamo la nostra isostatica di riferimento. I momenti X sono ovviamente incogniti e rappresentano le nostre incognite iperstatiche.

Step_3: Imporre la congruenza

I momenti X ed il carico Q adesso provocheranno delle rotazioni delle sezioni della trave a destra e a sinistra del carico opposte. Questa ipotesi tuttavia è puramente ipotetica perchè come sappiamo benissimo la trave in realtà è continua. Perciò adesso impostiamo che la rotazione data dai momenti e dal carico a destra e a sinistra dei carrelli sia uguale: 

Avendo risolto i momenti adesso possiamo trovare le reazioni vincolari.

Step_4: Determinare i diagrammi delle sollecitazioni 

Finora l’unico momento studiato è stato quello flettente. Con questa esercitazione entra in gioco anche il momento torcente.

La torsione esiste nel momento in cui due punti appartenenti all’elemento ruotano con velocità differenti intorno al proprio asse. 

L’elemento in questione reagirà in base alla rigidezza torsionale (Rt) data dalla geometria della sezione (momento polare d’inerzia Jt), dal materiale (modulo elastico tangenziale G) e dalla lunghezza.

Rt = (G * Jt) / l

M = Rt * φ

In questa esercitazione, come già detto, andremo a studiare una struttura che genera torsione.

La struttura è così semplificabile:

Questa struttura tridimensionale così semplificata è formata da 3 aste che, essendo nello spazio 3D, creano ognuna 6 GDV che sommati tra loro danno 18 GDV complessivi che, sottratti ai 6 GDL complessivi, generano una struttura 12 volte iperstatica.

Il momento, applicato nel nodo, genera nell’asta che si trova sulla sua linea d’asse deformazione di torsione mentre nelle altre genera flessione.

Questa risoluzione qualitativa è supportata da una serie di prove fatte in SAP2000 che hanno portato allo studio comparativo di varie sezioni in calcestruzzo e in acciaio che sono successivamente state tabellate per avere un semplice riscontro di quelli che sono i valori di spostamento e rotazione dell’asta che si torce. Ovviamente la sezione e il materiale delle due aste rimanenti è rimasto invariato con il valore di default in modo che i valori tabellati cambino solo in base alla sezione e materiale usato e non da agenti esterni.

Argomento di questo post sarà la descrizione della progettazione e verifica della struttura realizzata per l'edificio per uffici su via Ostiense, tema di laboratorio del corso Progettazione Architettonica 2M.

In particolare, senza entrare nel merito degli esiti del tema architettonico, saranno mostrate le modalità con le quali sono state portate avanti le diverse fasi progettuali relative alla struttura, i dimensionamenti e il disegno in pianta e prospetto.

L'intero post è realizzato (come specificato nel titolo) assieme a Giacomo Gasbarri.

A partire dall'impianto planimetrico è stata realizzata una griglia per stabilire quali dovessero essere i filidei pilastri (ipotizzando una ragionevole rastremazione) e come disporre i blocchi portanti per garantire luci sufficienti all'usufruibilità della particolare tipologia architettonica.

Noti dunque i carichi areali per i solai, le aree d'influenza a seconda se la trave sia principale o secondaria ed infine il numero di piani per blocco è stato possibile realizzare un utile foglio di calcolo (realizzato assieme a Fabio Liberati) per l'esecuzione di un dimensionamento a resistenza in tempo reale.

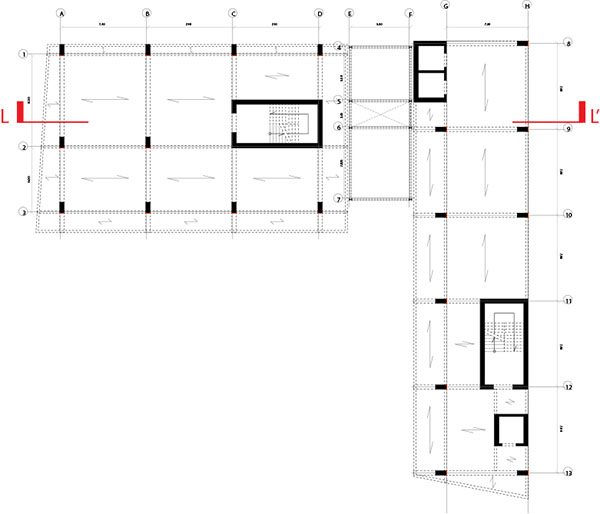
pianta quota +0,00

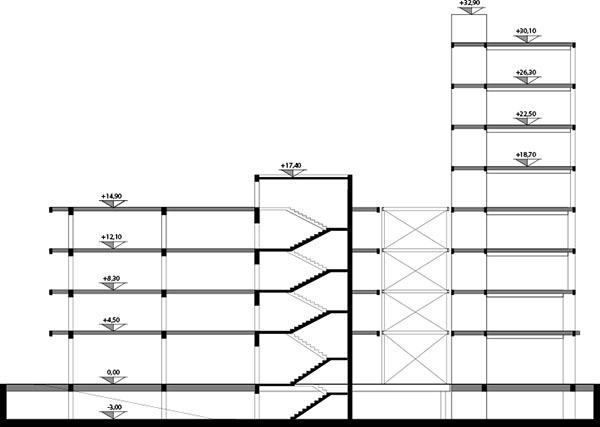
sezione L-L'

La tipologia strutturale è piuttosto standard ovvero una struttura a telaio in calcestruzzo armato con un blocco destinato al collegamento realizzato anch'esso a telaio ma in acciaio. Nello specifico del progetto è doveroso poi specificare che la struttura complessivamente si articola in 3 blocchi indipendenti così da sfavorire eventuali rotazioni dell'impalcato dovute a una sfavorevole posizione del centro delle rigidezze.

La suddivisione dell'edificio avviene dunque per impalcati rettangolari dove la posizione dei controventi vuole porsi l'obiettivo di rendere quanto più baricentrico il centro delle rigidezze. Lo stesso blocco di collegamento in acciaio è agganciato in maniera da perdere il suo legame con quelli in cemento attraverso fusibili e avere un comportamento autonomo in caso di sisma.

Per quanto riguarda il blocco in acciaio sono stati necessari controventamenti che per il principio secondo il quale sia sufficiente lunga un fila e una riga rispettivamente in pianta e alzato sono stati lungo le campate meno a vista o comunque in modo che non causino intralcio all'utenza.

Infine data la forte ottimizzazione della sezione necessaria nelle strutture in acciaio viene eseguita una prova all'instabilità per il pilastro.

Per tutte le fasi di dimensionamento (combinazione dei carichi, verifiche a resistenza, stabilità etc) si fa capo al testo Norme Tecniche per le Costruzioni integrate con la Circolare Applicativa e alle procedure illustrate nelle dispense del corso consentendo un dimensionamento non fortemente ottimizzato ma capace di garantire resistenza più che sufficiente alla struttura.

Per via della complessità della modellazione delle lastre a livello algebrico-analitico (specie attraverso il calcolo manuale) viene realizzato un modello di impalcato attraverso il software SAP2000 per il piano commerciale.

Facciamo presente (e questo può essere un feedback utile per chi si cimenterà nella realizzazione del proprio) che la modellazione è stata realizzata attraverso SAP poichè abbiamo riscontrato diversi errori nell'importazione da .dxf

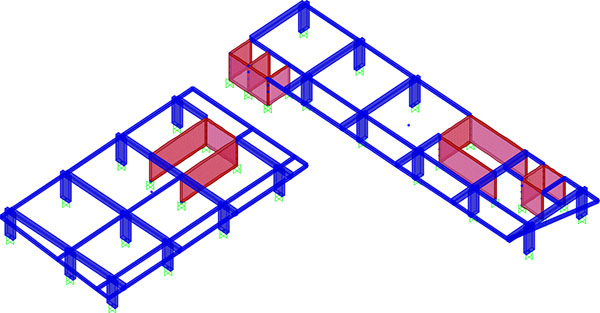
extrude view dell'impalcato

Attraverso l'extrude view si può osservare la gerarchia delle travi e la disposizione dei pilastri a seconda dell'appartenza all'impalcato. Per realizzare quest'ultima operazione si è realizzata una copia del profilo Pilastro e si sono invertiti i valori height e depth.

Nel foglio di calcolo e nel file .sap allegato sono presenti tutte le sezioni e gli interassi della struttura e dell'impalcato. Per una valutazione immediata eccoli qui elencati

- sezione pilastro CLS 40x120 cm
- sezione trave primaria CLS 40x70 cm
- sezione trave secondaria CLS 20x40 cm

- interasse pilastro 790 cm

Attraverso la selezione dei punti di colmo è stato aggiunto un Constraint di tipo Diaphraghm (Assign->Joint->Constraint->scegliere Diaphragm) per mezzo del quale sarà possibile assegnare un carico orizzontale che consentirà la valutazione della rotazione dell'impalcato.

Assegnato un carico orizzontale di 5000KN diretto verso Y (e poi verso X) la rotazione sul punto più esterno è dell'ordine di 10-5 unità, risultato che possiamo ritenere soddisfacente.

RIPARTIZIONE DELLE FORZE ORIZZONTALI IN UNA STRUTTURA IN CEMENTO ARMATO

In questo esercizio si analizza una struttura a telaio in cemento armato, con lo scopo di ricavare la rigidezza nei confronti delle forze orizzontali di ciascun telaio di cui essa è composta, la posizione del centro di massa della struttura, quella del centro delle rigidezze e in base alla distanza tra questi ultimi gli spostamenti che la struttura compie sotto l’azione di un sisma, considerando come si ripartiscono le forze orizzontali sui diversi telai.

Il primo passo consiste nel calcolare la rigidezza di ogni telaio in cemento armato. Questo valore è strettamente legato alla rigidezza dei singoli pilastri che lo compongono, definita dalla geometria e il materiale di cui sono composti.

In questa tabella sono riassunti i valori delle rigidezze di nostro interesse e le distanze a cui i telai si trovano rispetto all’origine, fissata nel vertice inferiore sinistro della pianta.

Successivamente vengono calcolate le coordinate del centro di massa, mediante una semplice media ponderata che considera la posizione del baricentro e l’area di ognuna delle figure archetipe in cui la pianta è suddivisa.

Il calcolo della posizione del centro delle rigidezze dipende dalla rigidezza dei singoli telai e dalla loro posizione rispetto all’origine. Una seconda media ponderata, che tiene conto della rigidezza totale lungo i 2 assi cartesiani di riferimento.

La sommatoria del prodotto tra la rigidezza di ogni telaio e il quadrato della sua distanza dal centro delle rigidezze porta al valore della rigidezza rotazionale. A parità di rigidezza infatti maggiore è la distanza che il telaio ha rispetto al centro delle rigidezze e maggiore è il contributo che fornisce nella limitazione degli spostamenti.

L’analisi dei carichi è necessaria per determinare la forza sismica che agisce sulla struttura. Infatti come è noto sono le strutture pesanti a soffrire di più i sismi. I carichi al metro quadro dei pesi permanenti e accidentali, moltiplicati per l’area dell’impalcato, per il coefficiente di contemporaneità e successivamente divisi per il coefficiente di intensità sismica portano al valore della forza sismica orizzontale.

L’ultimo passo consiste nel ricavare la forza che si ripartisce sui singoli telai. La forza sismica orizzontale è applicata sul centro delle masse, generando una traslazione dell’impalcato nella sua direzione: essa si determina dividendo la forza per la rigidezza nella direzione corrispondente. Ma la non coincidenza del centro delle masse con il centro delle rigidezze provoca anche una rotazione dell’impalcato, per via del momento torcente che in questo modo si genera, che dipende proprio dal prodotto tra la forza orizzontale equivalente e la differenza tra le ascisse e le ordinate dei 2 centri (che quindi portano ad avere 2 valori di momenti torcenti).

L’entità della rotazione dell’impalcato si ottiene dividendo i momenti torcenti per la rigidezza rotazionale. Queste 2 grandezze sono dimensionalmente coerenti, infatti la rotazione è adimensionale.

Grazie ai dati ottenuti è possibile calcolare la forza orizzontale che ogni telaio sarà chiamato a controventare. Nell’esempio preso in considerazione essa è per la maggior parte dovuta allo spostamento e in minima parte alla rotazione, per via dell’enorme differenza che sussiste tra la rigidezza rotazionale e quelle di traslazione (tra le 20 e le 40 volte più piccola) e del valore del momento torcente, che è solo la metà della forza sismica orizzontale.

In questa esercitazione dovremo analizzare un impalcato strutturale soggetto a forze orizzontali. Lo studio verterà sul calcolo della rigidezza traslante K_δ, della traslazione δ lungo la direzione della forza agente, sulla rigidezza rotazionale K_φ e quindi sulla rotazione φ intorno al centro delle rigidezze.

Questo impalcato è formato da 7 telai ognuno dei quali comprende pilastri di grandezza 30x20cm, da cui i momenti d’inerzia:

STEP 1

In questo step si tabellano i telai dando ad ognuno dei dati precisi che sono: modulo di Young (E), altezza H e i valori dei momenti d’inerzia per ogni pilastro in base all’asse di rotazione. Si può quindi procedere al calcolo della rigidezza traslante K_δ di ogni telaio.

K_δ = ΣK_δ                Κ = 12EI/h³

STEP 2

In questo step raccoglieremo tutte le informazioni analitiche delle distanze dei vari telai da un punto di origine O e i valori delle rigidezze traslanti dei telai.

STEP 3

Ora bisognerà trovare il centro delle masse. Il passaggio è abbastanza semplice: si divide la forma della pianta in forme semplici con cui abbiamo facilità nel trovare il baricentro, a questo punto si tratta solo di attuare una media ponderata tra le aree delle suddette forme semplici e moltiplicarle con le distanze dal punto di origine.

G_X = [(X₁*A₁)+ (X₂*A₂)] / A_TOT

G_Y = [(Y₁*A₁)+ (Y₂*A₂)] / A_TOT

STEP 4

Quindi ora si passa alla determinazione del centro delle rigidezze (C).

X_C = (∑_i K_iv * d_iv) / K_{v_tot}                       Y_C = (∑_i K_io * d_io) / K_{o_tot}

Una volta trovato il centro delle rigidezze si dovranno calcolare le distanze di ogni telaio da C. A questo punto siamo in grado di calcolare la rigidezza torsionale K_φ.

Kφ = ∑i Ki * ddi2

STEP 5

Si esegue ora l’analisi dei carichi sismici allo SLE (perché non viene tenuto in conto γ) tramite il carico permanente totale G (somma dei carichi per l’area dell’impalcato) ed il carico totale accidentale Q (carico accidentale per l’area). Ne consegue che vi possiamo determinare i pesi sismici W: W = G + (Q * y).          y=coefficiente di contemporaneità.

Si procede dunque a trovare la forza sismica orizzontale F: F = W / c.    c=coefficiente di intensità sismica.

STEP 6-7

Siamo quindi in grado di quantificare la forza sismica orizzontale F lungo i due assi x/y per ogni controvento. Non essendo nello stesso punto il centro delle masse e il centro delle rigidezze il sistema ruoterà dando vita ad una traslazione δ ed una rotazione σ. Questa rotazione genera un momento torcente M che dovremo andare a calcolare.

Asse X:

M = F *(Y_c – Y_G)

F_oi = K_oi (u_x + dd_oi * φ)

F_vi = K_vi (dd_vi * φ)

Asse Y:

M = F *(X_c – Y_G)

F_oi = K_oi (dd_oi * φ)

F_vi = K_vi (u_y + dd_vi * φ)