Esercitazione_8.0
rigidezza torsionale (risoluzione a mano e tramite software SAP2000)
1_
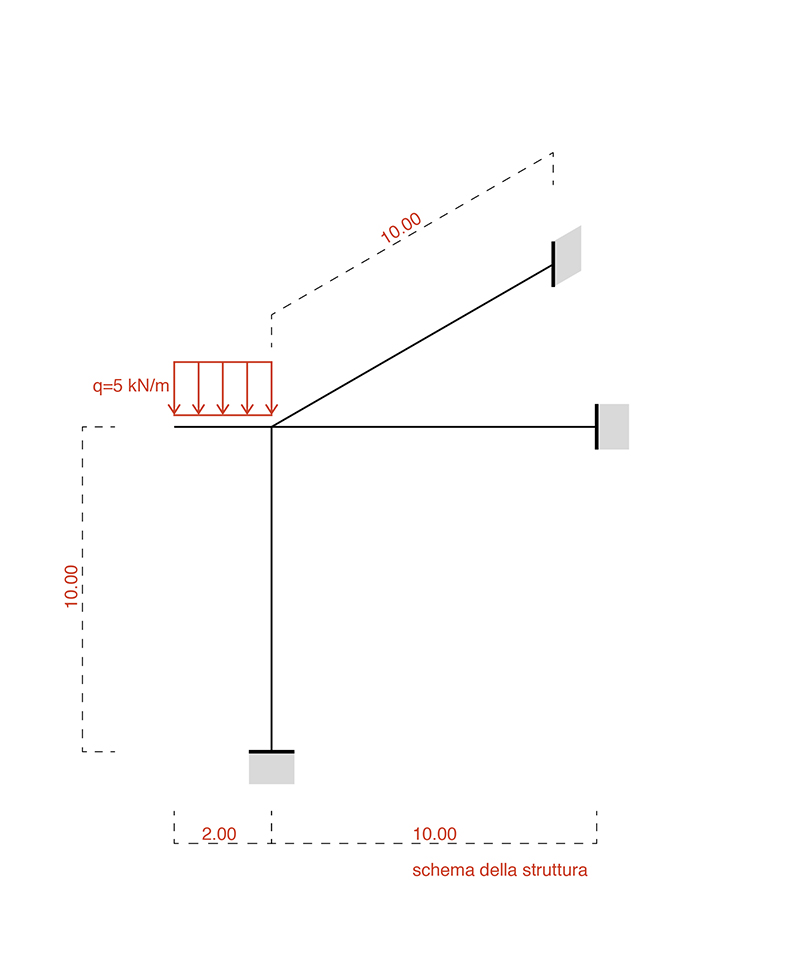
Il sistema proposto risulta essere un sistema tridimensionale composto da travi e pilastri di lunghezza 10m, e da un aggetto di lunghezza 2m con un carico uniformemente distribuito pari a 5 kN/mq. Lo scopo dello studio del sistema risulta essere quello di comprendere come la sezione ed il materiale della trave soggetta a torsione influiscano su quest’ultima a parità di azioni esterne.
2_
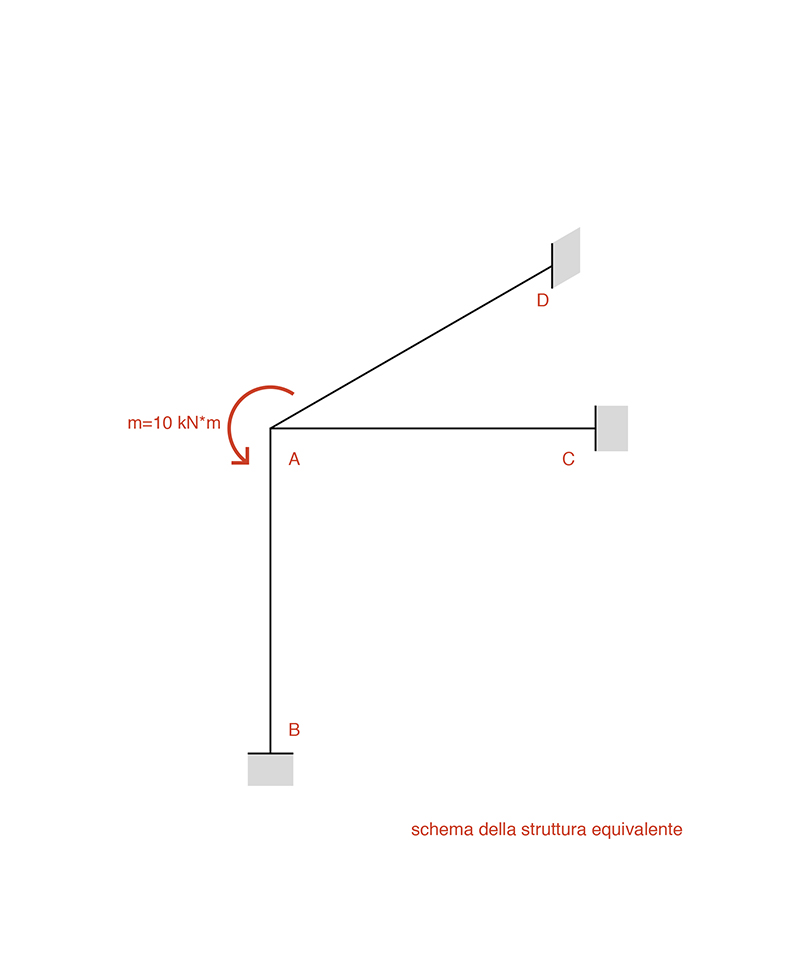
Per poter studiare la struttura in maniera più semplice, quest’ultima viene studiata tramite uno schema equivalente dove l’aggetto soggetto al peso uniformemente distribuito viene eliminato e vi è applicato un momento concentrato M= (q*L²)*1/2. L’azione del momento applicato genera una flessione nella trave e nel pilastro posizionati nel piano XZ, ed una torsione nella trave posizionata nel piano YZ.
3_
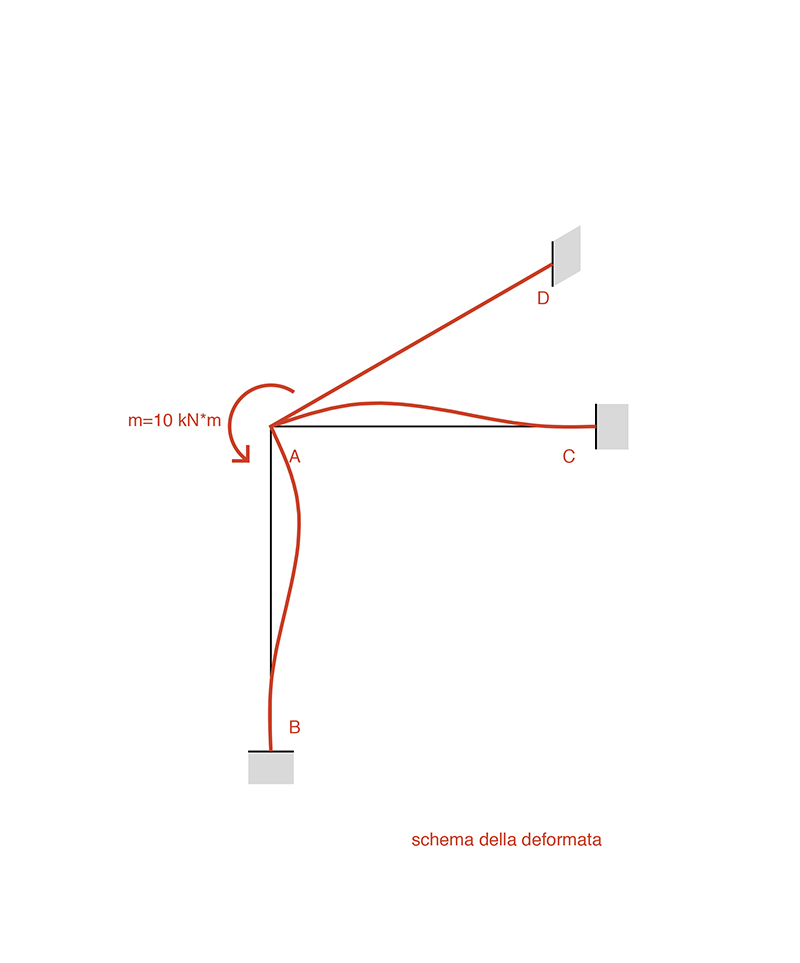
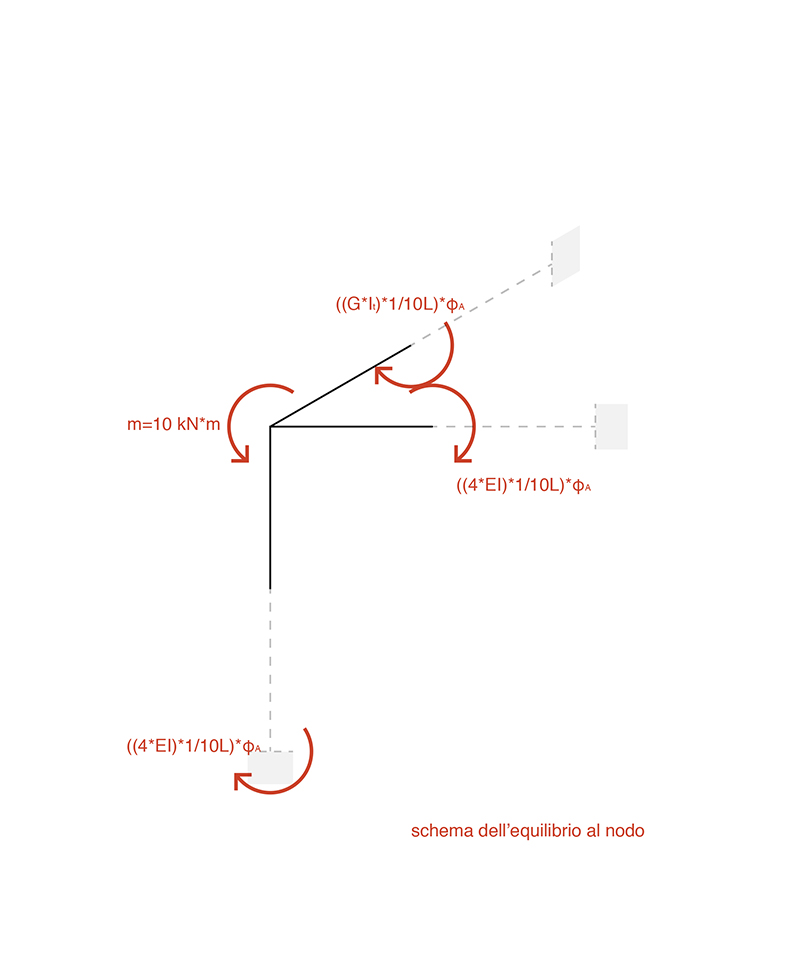
Dopo aver studiato la deformata della struttura si puo ricavare di conseguenza il grafico qualitativo dei momenti, nel quale l’unica incognita presente risulta essere la rotazione φA (la rotazione sarà uguale in quanto abbiamo supposto che il nodo A sia un nodo rigido).
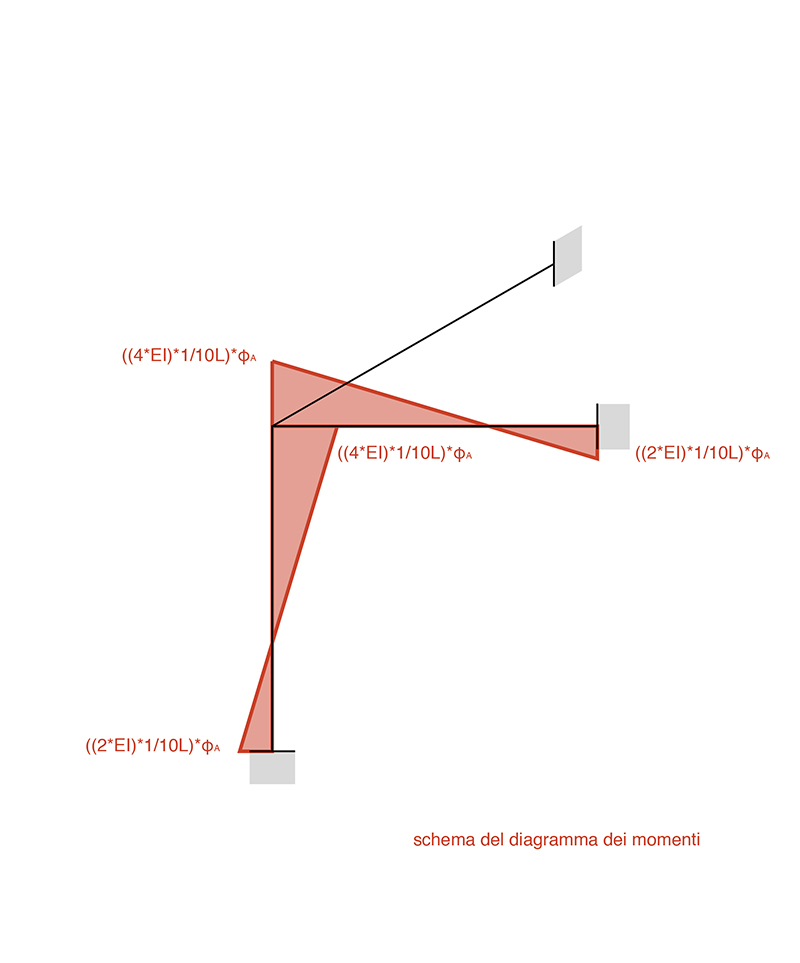
Successivamente si procederà studiando l’equilibrio del nodo, e definendone la sua rigidità.
Eq. nodo A => (q*L²)*1/2 - (((4*E*I)*1/10*L)*φA) - (((4*E*I)*1/10*L)*φA) - (((G*It)*1/10*L)*φA) = 0
=> (q*L²)*1/2 = (((4*E*I)*1/10*L)*φA) + (((4*E*I)*1/10*L)*φA) + (((G*It)*1/10*L)*φA)
=> (q*L²)*1/2 = φA*(((4*E*I)*1/10*L) + ((4*E*I)*1/10*L) + ((G*It)*1/10*L))
rigidezza del nodo A => RA = ((4*E*I)*1/10*L) + ((4*E*I)*1/10*L) + ((G*It)*1/10*L)
=> RA = ((q*L²)*1/2)*1/φA)
=> φA = ((q*L²)*1/2)*1/RA)
trave AC MAC= - (((4*E*I)*1/10*L)*φA)
trave AD MAD= - (((G*It)*1/10*L)*φA)
pilastro AB MAB= - (((4*E*I)*1/10*L)*φA)
Eq. nodo A => (q*L²)*1/2 = MAC + MAB + MAD
4_
Possiamo ora attraverso le formule sopra ricavate calcolare la rotazione φA ed il momento torcente MAD:
(q*L²)*1/2
E (in funzione del materiale che viene impiegato nella sezione)
Ix= ((B*H³)*1/12)
G= E*(1/2*(1+ν)) (dove ν è il coefficiente di Poisson che dipende dal materiale impiegato nella sezione)
It= c2*a*b³ (dove c2 è un coefficiente tabellato che tiene conto del rapporto del lato maggiore sul lato minore della sezione a/b)
|
a/b
|
c1
|
c2
|
|
1
|
0,208
|
0,1406
|
|
1,2
|
0,219
|
0,1661
|
|
1,5
|
0,231
|
0,1958
|
|
2
|
0,246
|
0,229
|
|
2,5
|
0,248
|
0,249
|
|
3
|
0,267
|
0,263
|
|
4
|
0,282
|
0,281
|
|
5
|
0,291
|
0,291
|
|
10
|
0,312
|
0,312
|
|
∞
|
0,333
|
0,333
|
Successivamente andremmo a studiarci le seguenti sezioni attraverso un foglio Excel ed il software SAP2000:
1.1 sezione quadrata cava r= 20cm tw= 1cm
1.2 HEA 220
1.3 sezione circolare cava r= 20cm tw= 1cm
2.1 sezione rettangolare 15cm _ 67cm
2.2 sezione circolare 36cm
5_
Successivamente alla risoluzione a mano del sistema del nodo si procede con la verifica tramite il software SAP.
La modellazione viene effettuata per comodità direttamente in SAP.
creare un nuovo file con una griglia utile al disegno dell’asta:
FILE > NEW MODEL >
QUICK GRID LINES > impostare 6 assi sull’asse x, 2 sull’asse y e 2 sull’asse z > impostare come GRID SPACING la dimensione che vorremo dare alla lunghezza della trave
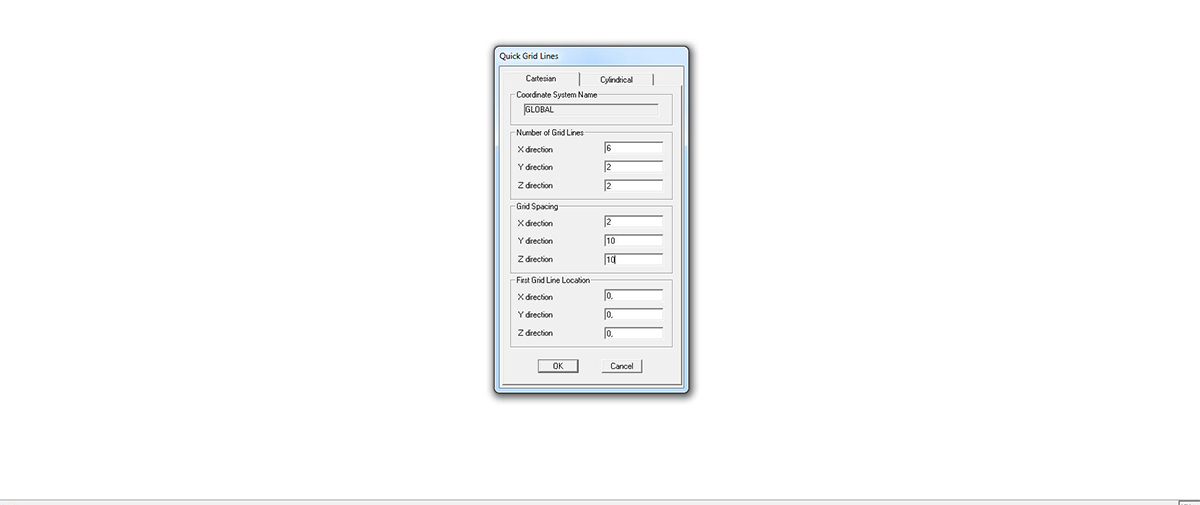
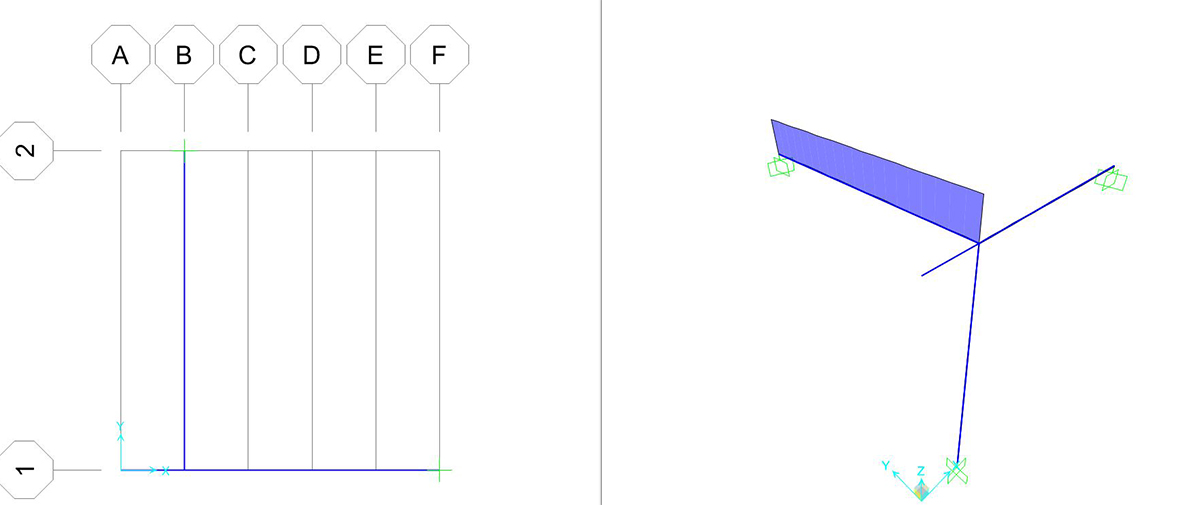
le impostazioni date alla griglia dovrebbero produrre una condizione analoga alla seguente:
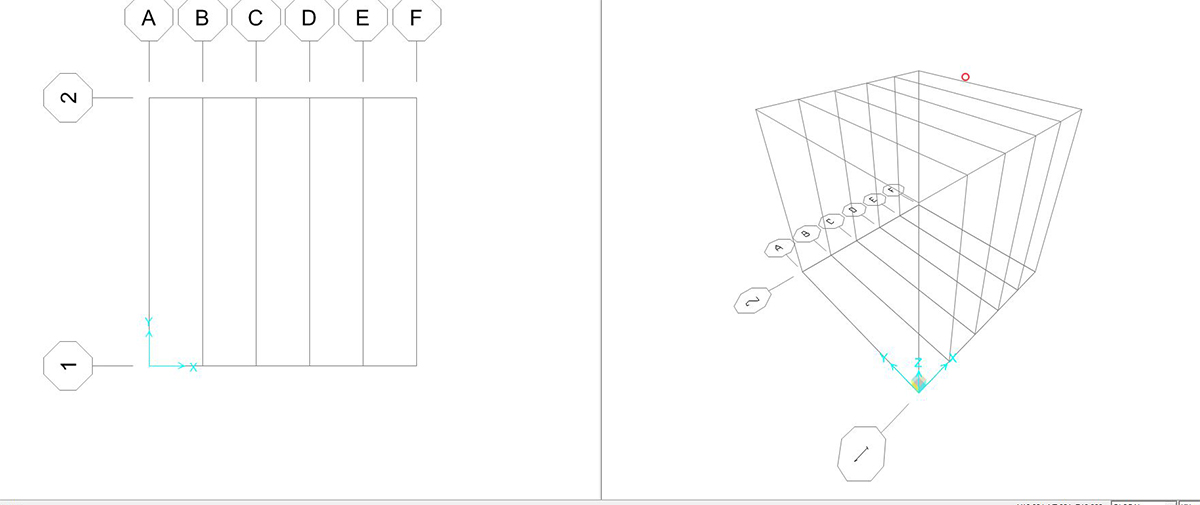
disegnare le aste della trave seguendo la spaziatura della griglia preimpostata.
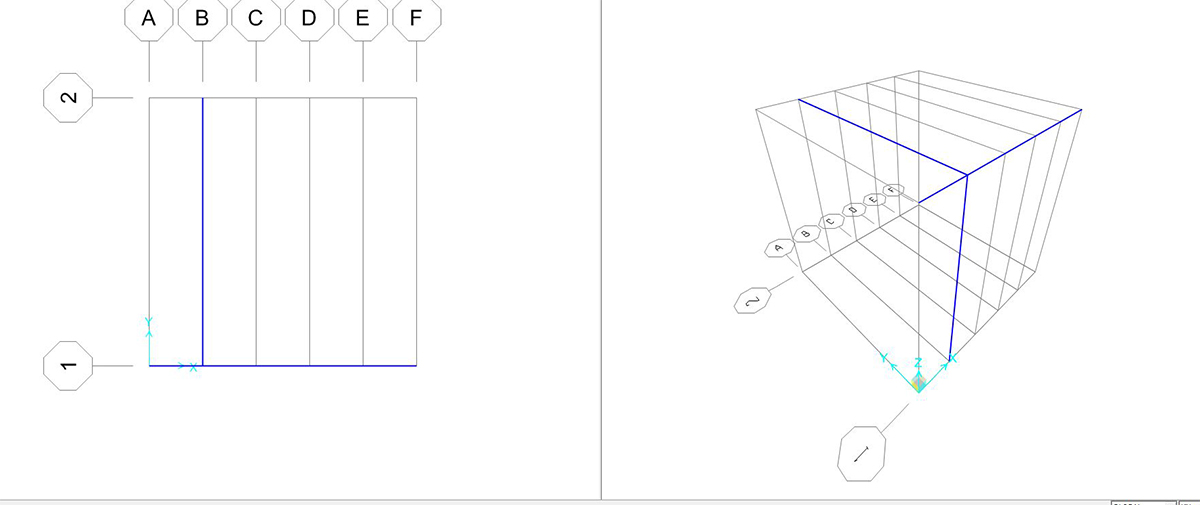
assegnare i vincoli:
selezionare il punto > ASSIGN > JOINT RESTRAINTS > spuntare le sollecitazioni che il vincolo da posizionare trattiene
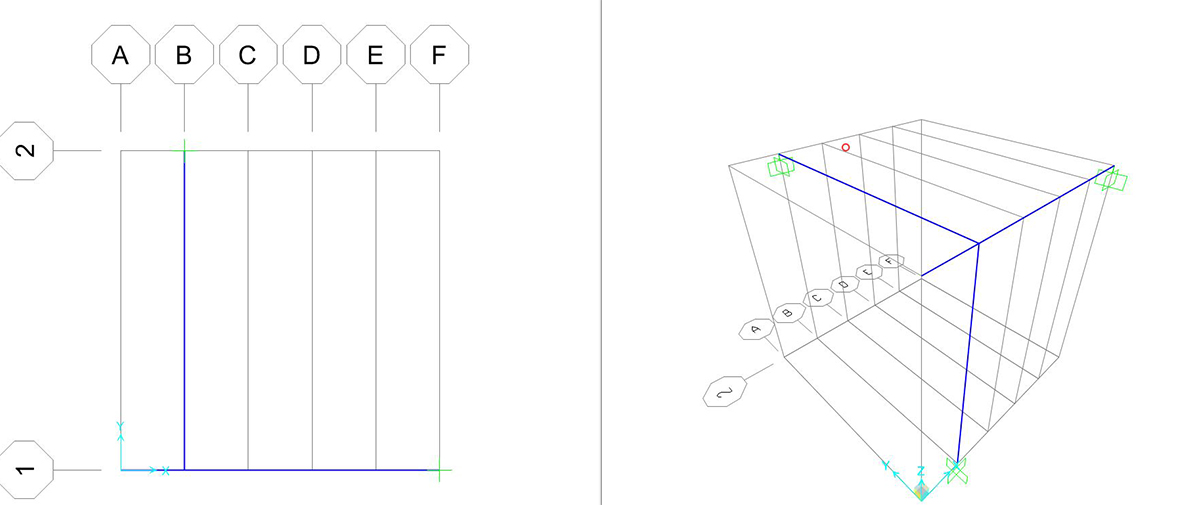
vengono assegnati incastri sulle 3 aste
N.B. In questo tipo di esercizi, impostiamo l’analisi in modo che non consideri il peso proprio della struttura (che costituirebbe un carico distribuito su travi che si deve considerare scariche).
Ciò viene fatto creando un nuovo LOAD PATTERN che abbia 0 come coefficiente di moltiplicazione del carico SELF WEIGHT MULTIPLER.
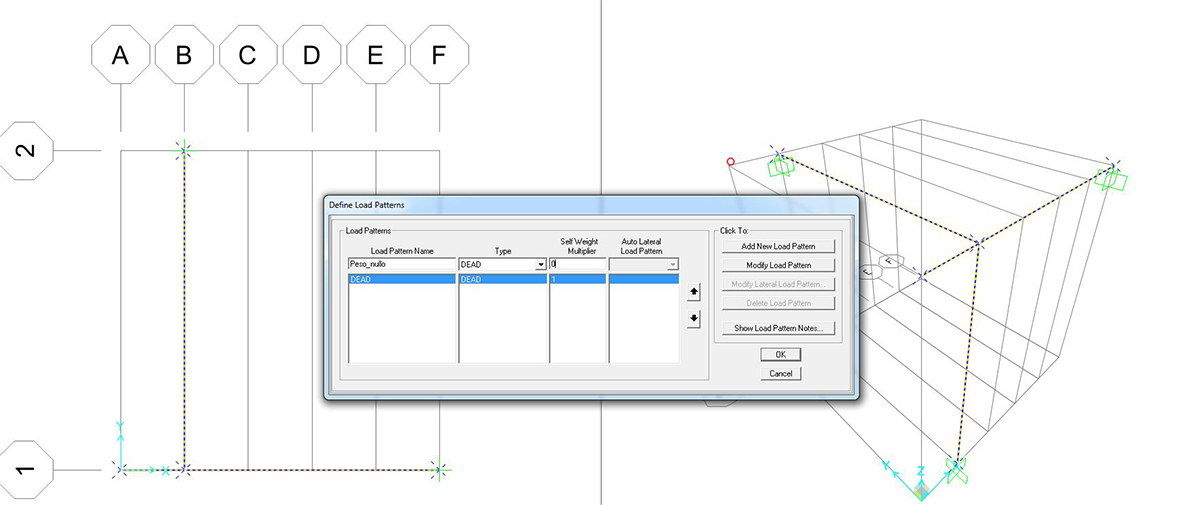
Si procede con l’assegnazione dei carichi con il comando ASSIGN > JOINT LOADS > DISTRIBUTED, trattandosi di un’idealizzazione per la quale i carichi sono distribuiti.
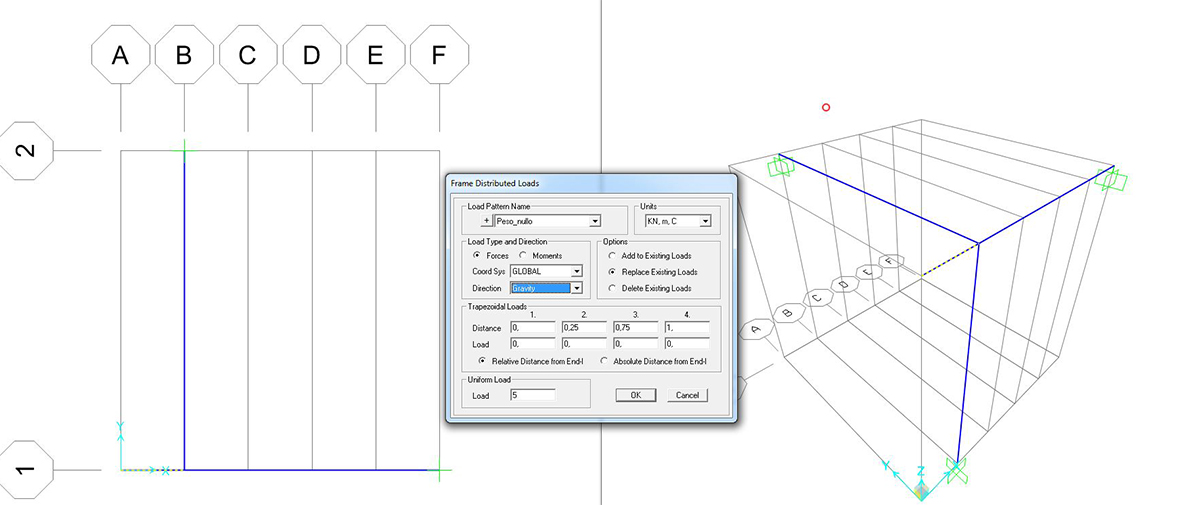
N.B. si possono anche analizzare gli sforzi a cui sono sottoposti i vincoli dando il comando SHOW FORCES/STRESSES > JOINTS.
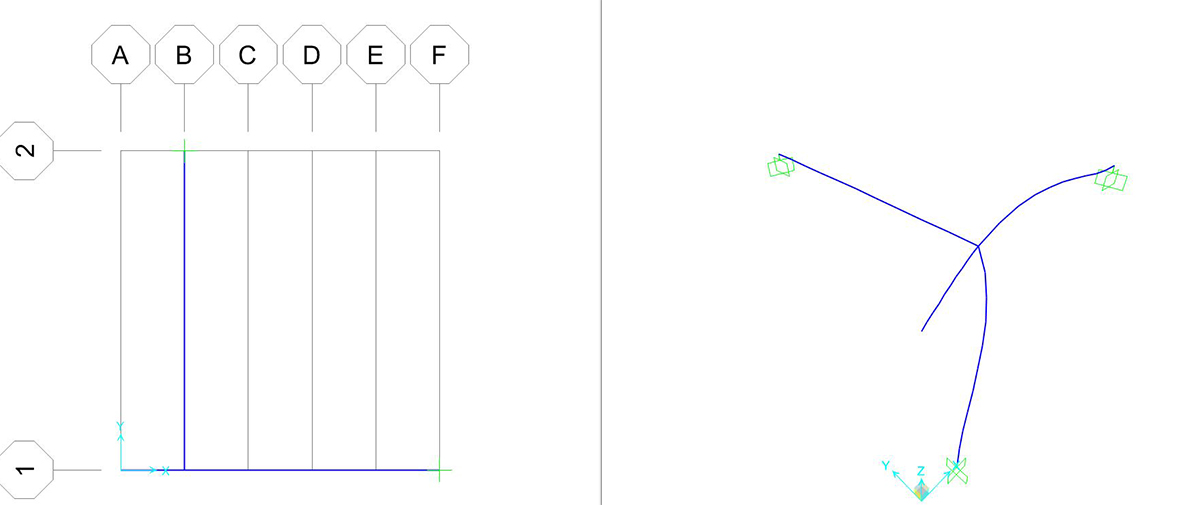
Possiamo ora avviare l’analisi. Il software mostra per prima cosa l’andamento della deformata.
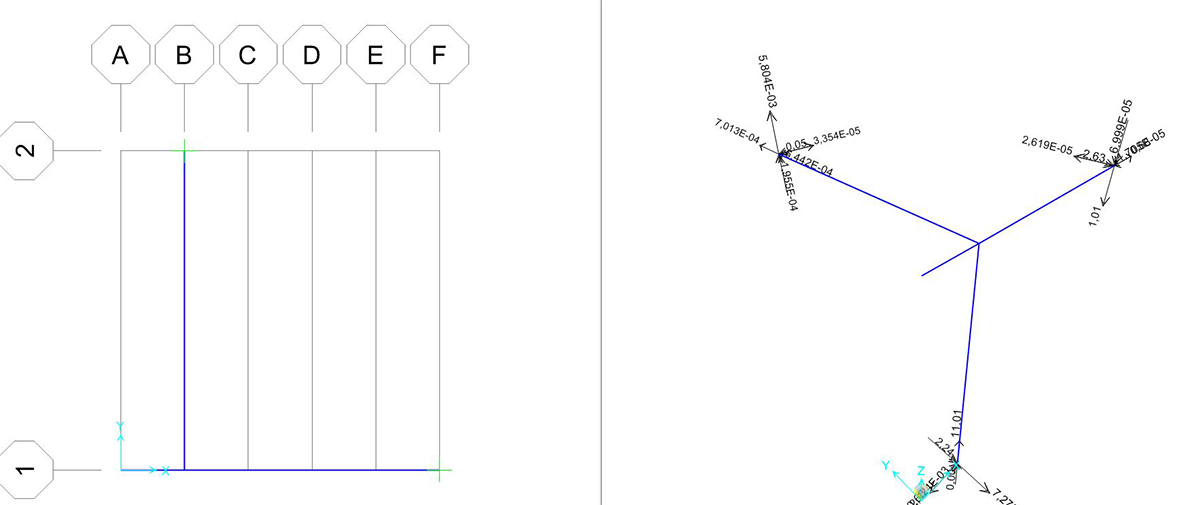
Si può richiedere al programma di analizzare gli sforzi assiali (unici presenti) con il comando SHOW FORCES/STRESSES > FRAME/CABLES > SHEAR 22
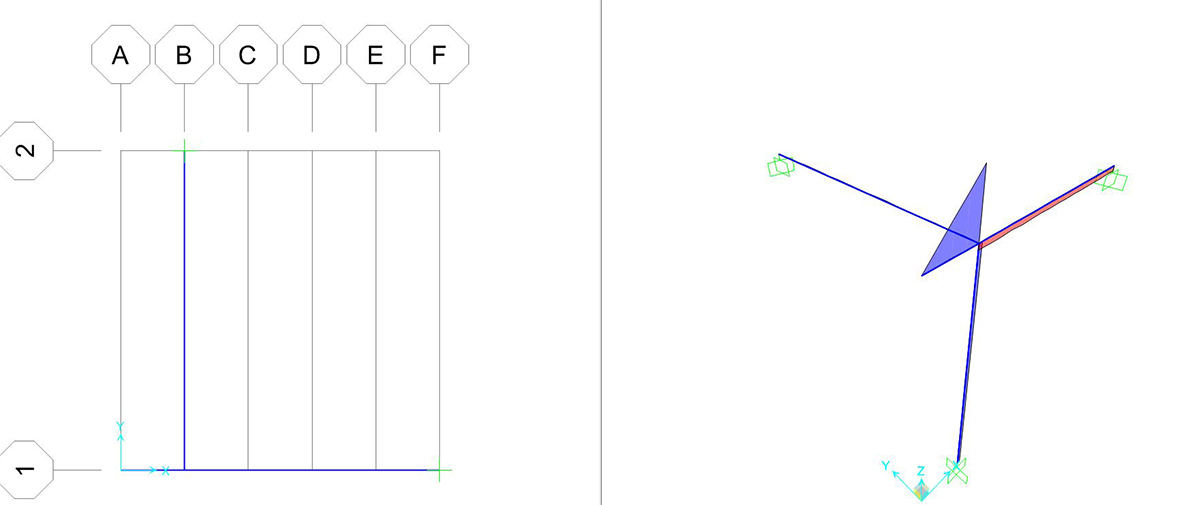
Si può richiedere al programma di analizzare gli sforzi assiali (unici presenti) con il comando SHOW FORCES/STRESSES > FRAME/CABLES > MOMENT 33
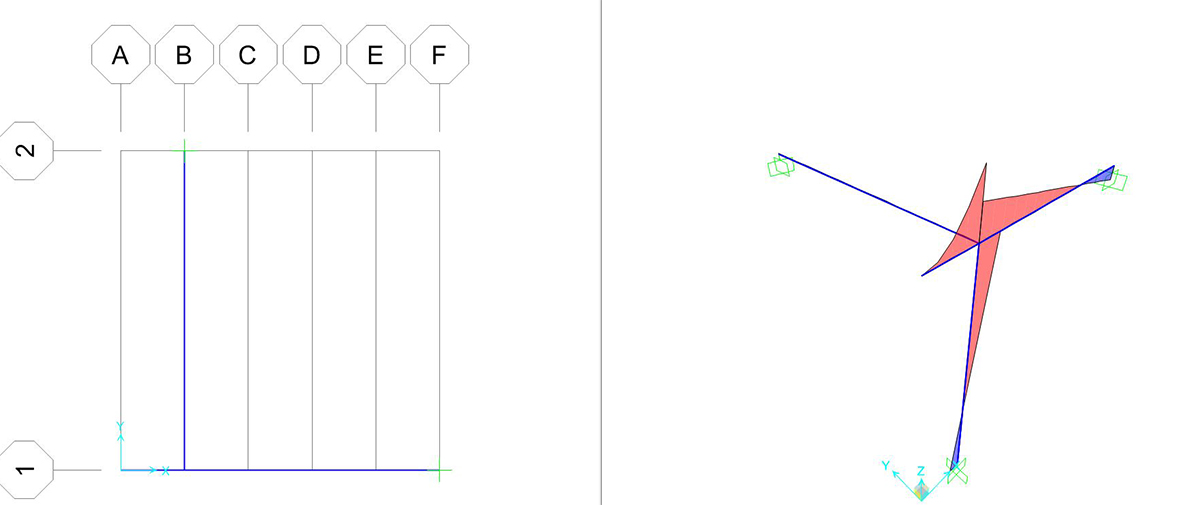
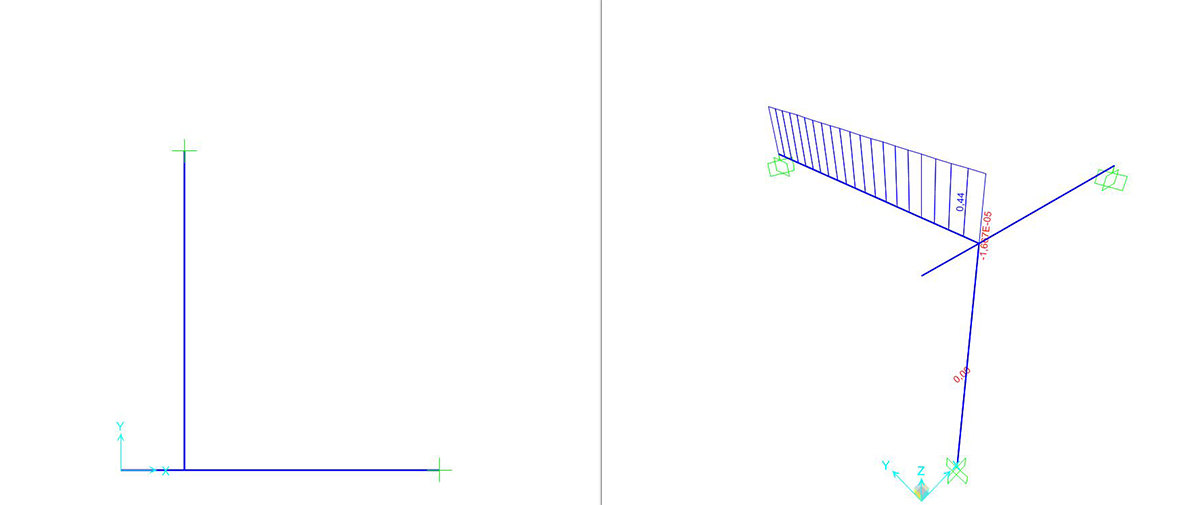
Si può richiedere al programma di analizzare gli sforzi assiali (unici presenti) con il comando SHOW FORCES/STRESSES > FRAME/CABLES > TORSION
Possiamo ora avviare l’analisi della struttura in funzione delle varie sezioni assegnate.
ACCIAIO
SEZIONE QUADRATA CAVA
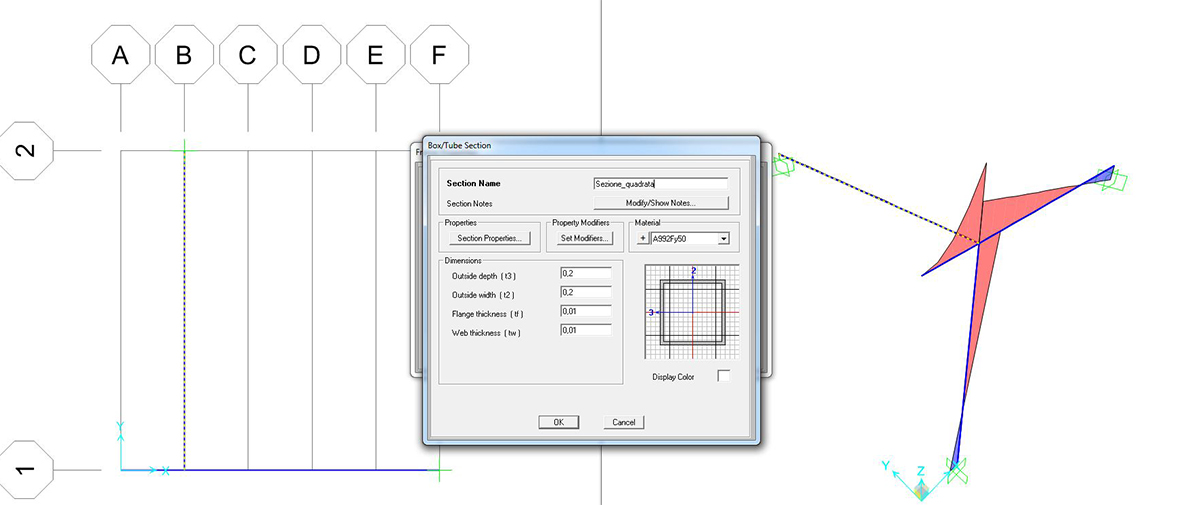
Si può richiedere al programma di analizzare gli sforzi assiali (unici presenti) con il comando SHOW FORCES/STRESSES > FRAME/CABLES > TORSION
|
ACCIAIO_sezione quadrata cava r= 20cm tw= 1cm
|
|
|
M1
|
M2
|
M3
|
|
|
|
385,182
|
385,182
|
240,065
|
|
|
RA
|
|
|
|
1.010,429
|
|
φA
|
|
|
|
|
|
|
(q*L²)*1/2
|
RA
|
|
|
|
|
10
|
1.010,429
|
|
|
|
φA
|
|
|
0,009897
|
|
|
|
|
|
|
|
|
|
M1
|
M2
|
M3
|
|
|
|
3,812
|
3,812
|
2,376
|
|
|
equilibrio
|
|
|
|
10,000
|
HEA 200
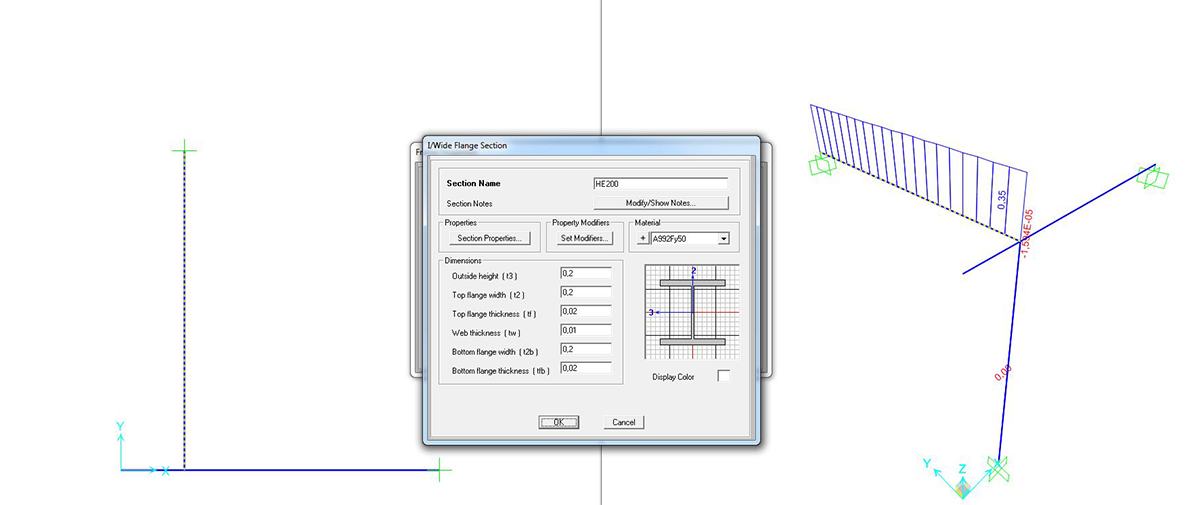
Si può richiedere al programma di analizzare gli sforzi assiali (unici presenti) con il comando SHOW FORCES/STRESSES > FRAME/CABLES > TORSION
|
ACCIAIO_sezione HEA 200
|
|
|
M1
|
M2
|
M3
|
|
|
|
575,232
|
575,232
|
0,810
|
|
|
RA
|
|
|
|
1.151,274
|
|
φA
|
|
|
|
|
|
|
(q*L²)*1/2
|
RA
|
|
|
|
|
10
|
1.151,274
|
|
|
|
φA
|
|
|
0,008686
|
|
|
|
|
|
|
|
|
|
M1
|
M2
|
M3
|
|
|
|
4,996
|
4,996
|
0,007
|
|
|
equilibrio
|
|
|
|
10,000
|
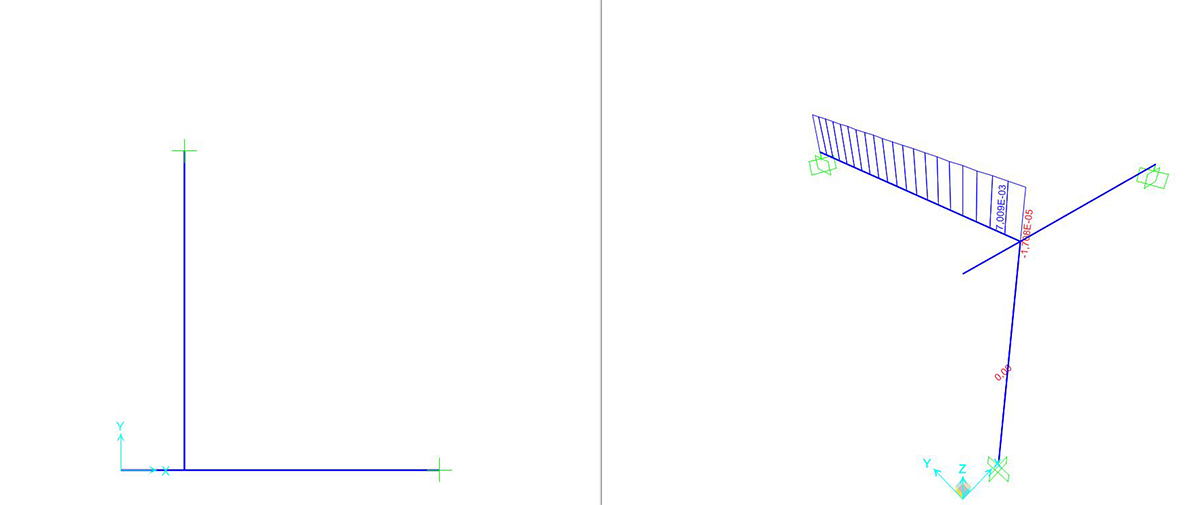
SEZIONE CIRCOLARE CAVA
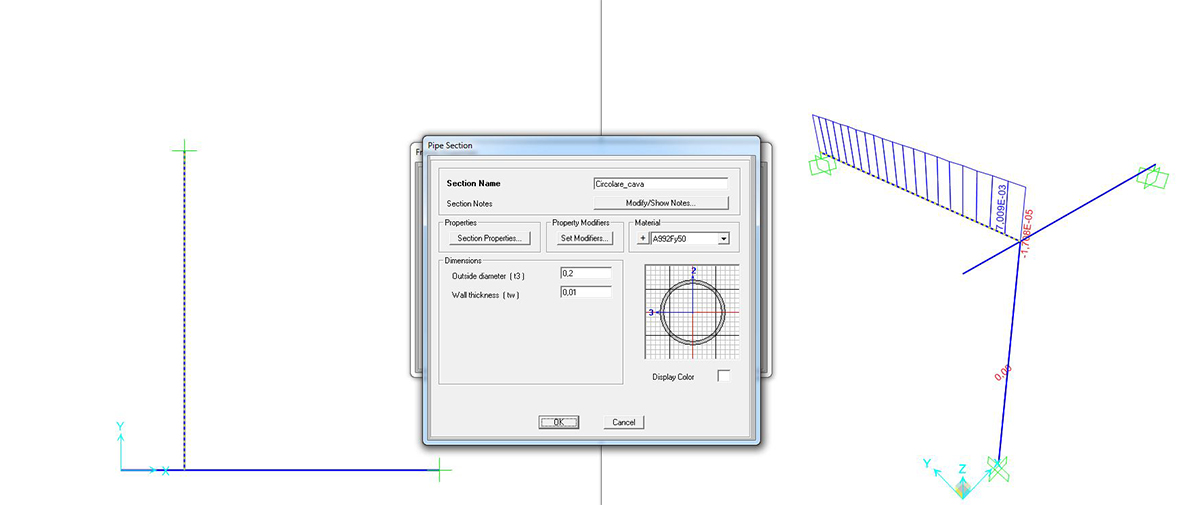
Si può richiedere al programma di analizzare gli sforzi assiali (unici presenti) con il comando SHOW FORCES/STRESSES > FRAME/CABLES > TORSION
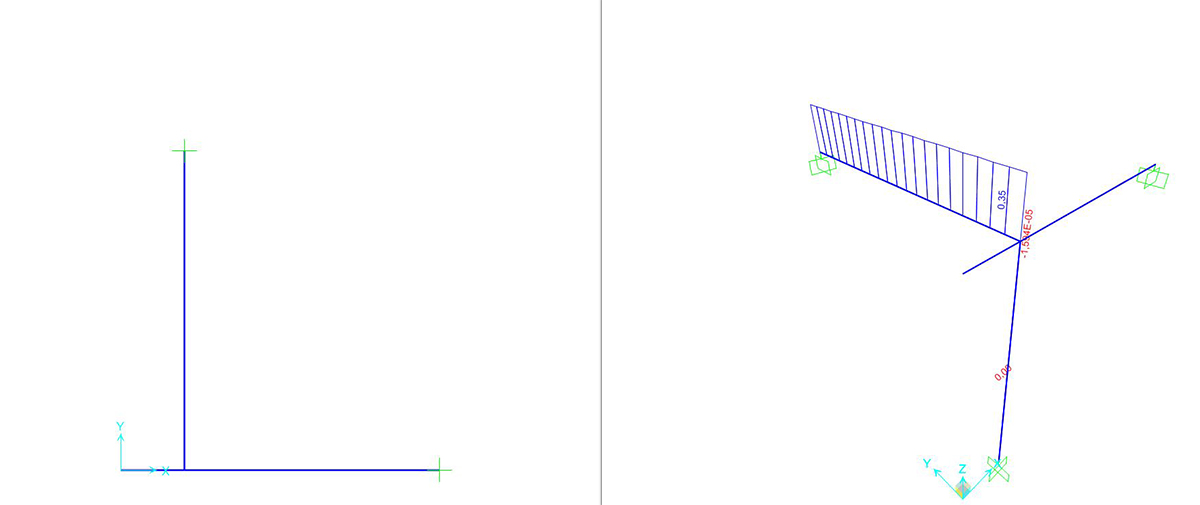
|
ACCIAIO_sezione circolare cava r= 20cm tw= 1cm
|
|
|
M1
|
M2
|
M3
|
|
|
|
226,884
|
226,884
|
1.987,313
|
|
|
RA
|
|
|
|
2.441,081
|
|
φA
|
|
|
|
|
|
|
(q*L²)*1/2
|
RA
|
|
|
|
|
10
|
2.441,081
|
|
|
|
φA
|
|
|
0,004097
|
|
|
|
|
|
|
|
|
|
M1
|
M2
|
M3
|
|
|
|
0,929
|
0,929
|
8,141
|
|
|
equilibrio
|
|
|
|
10,000
|
CA
SEZIONE RETTANGOLARE 15cm_67cm
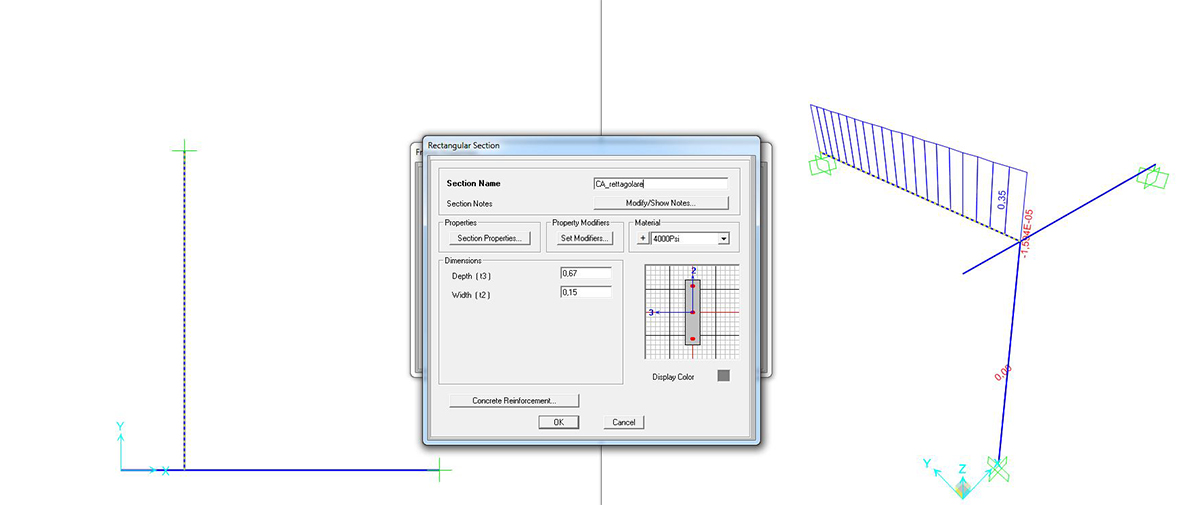
Si può richiedere al programma di analizzare gli sforzi assiali (unici presenti) con il comando SHOW FORCES/STRESSES > FRAME/CABLES > TORSION
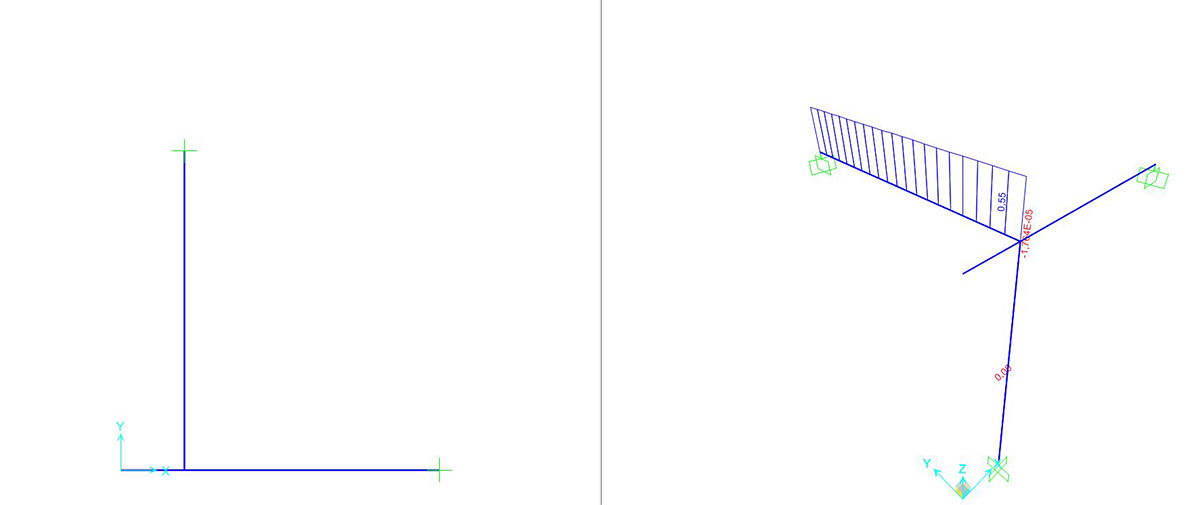
|
CA_sezione rettangolare 15cm _ 67cm
|
|
|
M1
|
M2
|
M3
|
|
|
|
31.580,115
|
31.580,115
|
555,985
|
|
|
RA
|
|
|
|
63.716,215
|
|
φA
|
|
|
|
|
|
|
(q*L²)*1/2
|
RA
|
|
|
|
|
10
|
63.716,215
|
|
|
|
φA
|
|
|
0,000157
|
|
|
|
|
|
|
|
|
|
M1
|
M2
|
M3
|
|
|
|
4,956
|
4,956
|
0,087
|
|
|
equilibrio
|
|
|
|
10,000
|
SEZIONE CIRCOLARE 36cm
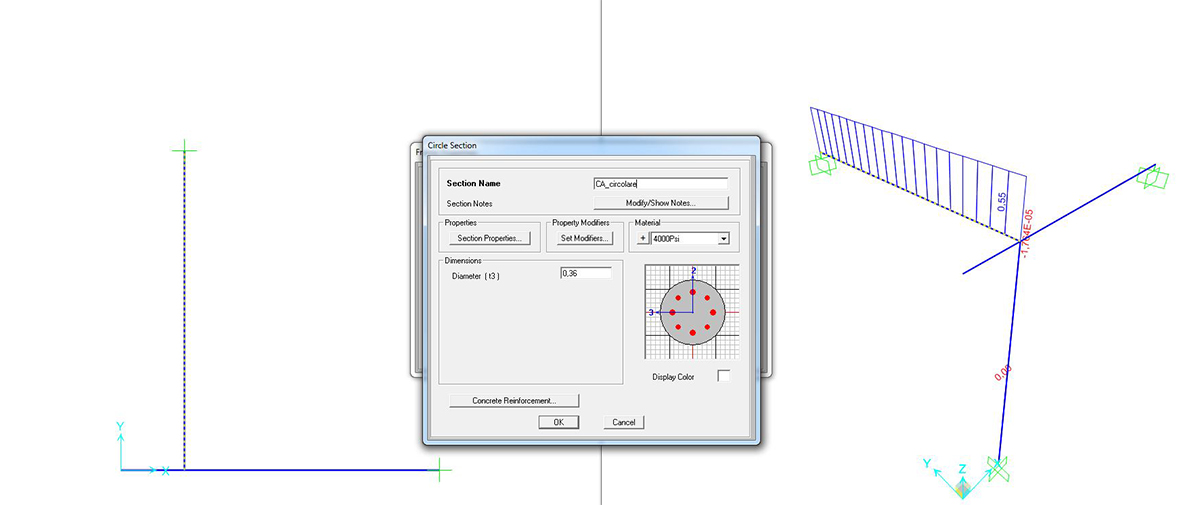
Si può richiedere al programma di analizzare gli sforzi assiali (unici presenti) con il comando SHOW FORCES/STRESSES > FRAME/CABLES > TORSION
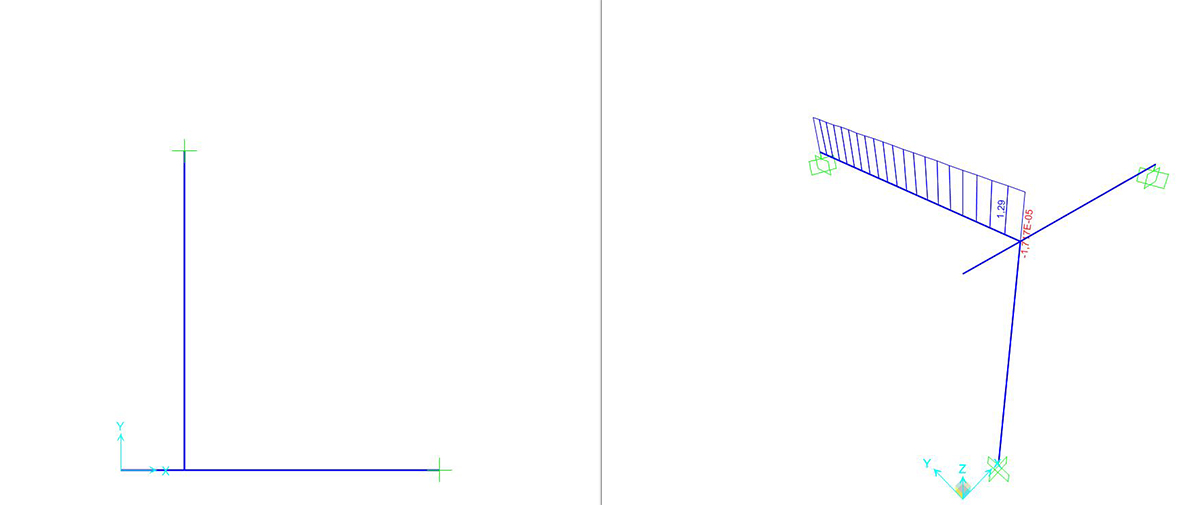
|
CA_sezione circolare r= 36cm
|
|
|
M1
|
M2
|
M3
|
|
|
|
110.810,055
|
110.810,055
|
5.771,357
|
|
|
RA
|
|
|
|
227.391,467
|
|
φA
|
|
|
|
|
|
|
(q*L²)*1/2
|
RA
|
|
|
|
|
10
|
227.391,467
|
|
|
|
φA
|
|
|
0,000044
|
|
|
|
|
|
|
|
|
|
M1
|
M2
|
M3
|
|
|
|
4,873
|
4,873
|
0,254
|
|
|
equilibrio
|
|
|
|
10,000
|
Commenti recenti