Blog

 

Avrei potuto scrivere una dispensa sulla torsione.

Invece vi ho selezionato contenuti disponibili in rete, di docenti che condividono la stessa filosofia open access di questo portale. Queste due dispense sono abbastanza semplici e soprattutto esaustive, nei limiti dei nostri obiettivi formativi.

In aggiunta, ho inserito due file excel, relativi a due sezioni quadrate cave in parete sottile, l'una di profilo chiuso, l'altra di profilo aperto. Calcolano il momento di inerzia a flessione e a torsione delle due sezioni.
Questa esemplificazione serve a mostrarvi che la presenza della fessura nel profilo ha piccole conseguenze nel caso della flessione e grandi conseguenze nel caso di torsione.

Buon lavoro

la prof.

Avendo già svolto l'esercitazione nell'anno accademico 2020/21, le alleghiamo il link che riporta al blog dell'esercitazione riguardante il progetto di una travatura reticolare spaziale. 

http://design.rootiers.it/strutture/node/2814

Dopo aver rivisto l'elaborato relativo alla prima esercitazione ci siamo resi conto di aver sbagliato il calcolo del peso proprio della travatura reticolare (Pp). Per distrazione, abbiamo calcolato le reazioni vincolari con un modello di carico sbagliato: invece di utilizzare il modello di carico che considerasse il peso proprio delle aste (DEAD) abbiamo utilizzato il modello di carico allo stato limite ultimo (Qu). Per questo motivo il peso proprio della struttura risulta sbagliato e sovraccaricato, dunque l'analisi agli abbassamenti non è verificata. 

P.S.

scusi per il ritardo

Studenti: Davide Grande, Esther Grassi, Priscilla Piazzolla, Emanuele Soverini

La travatura reticolare ricopre un’area trapezoidale di 396 m², cioè:

B= 36m

b=30m

l₁=12m

l₂=13,4m

 

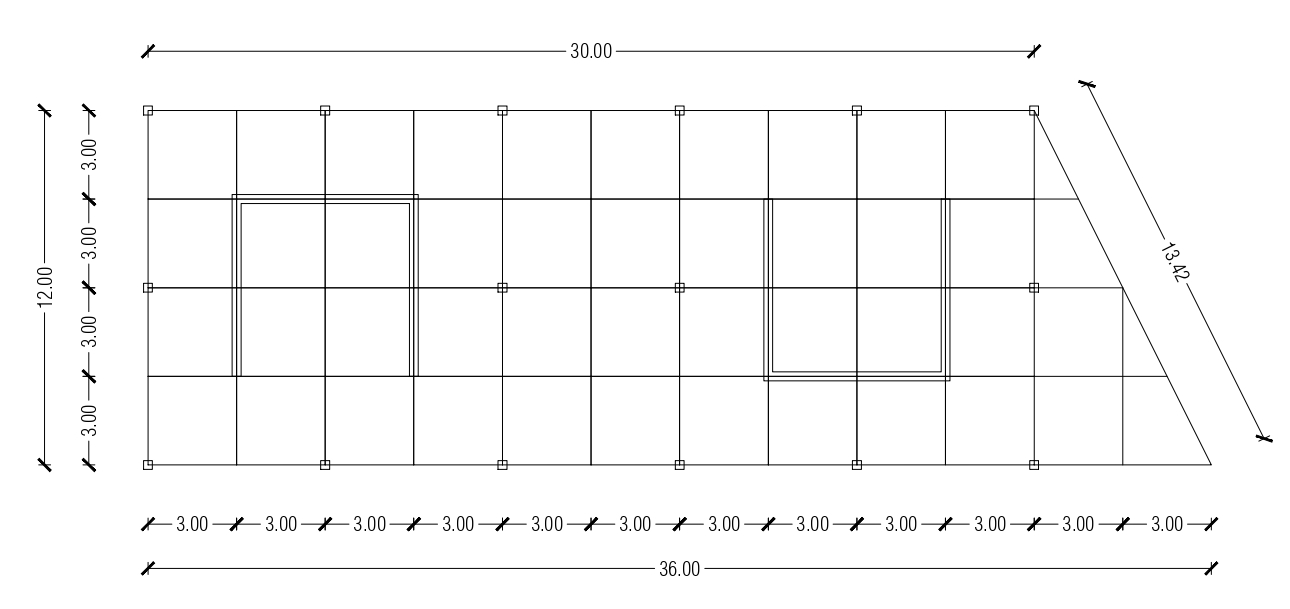
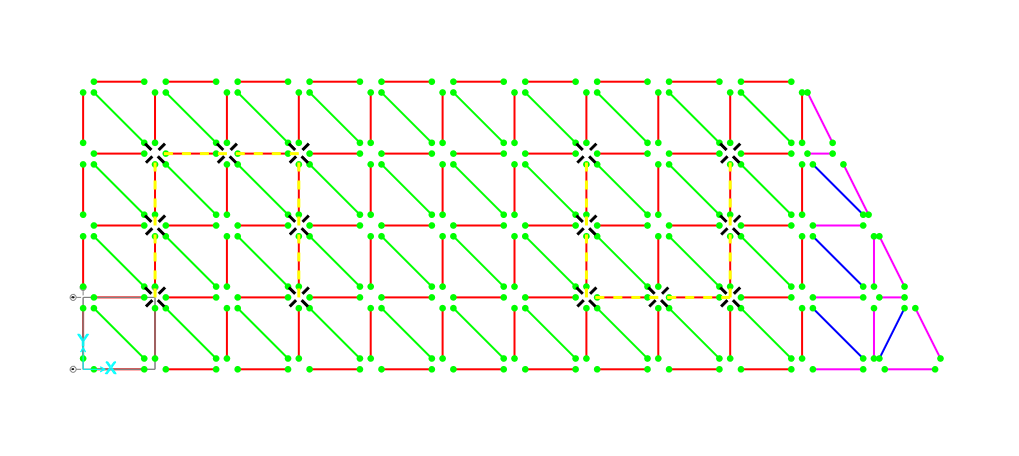
Ogni modulo cubico è pari a 3 x 3 x 3 m (definisco l=3, d=3√2) quindi è composta da 10 x 4 moduli con l’aggiunta di una porzione irregolare.

Posizioniamo I setti a C e i pilastri in modo da esser collegati ai nodi della travatura reticolare.

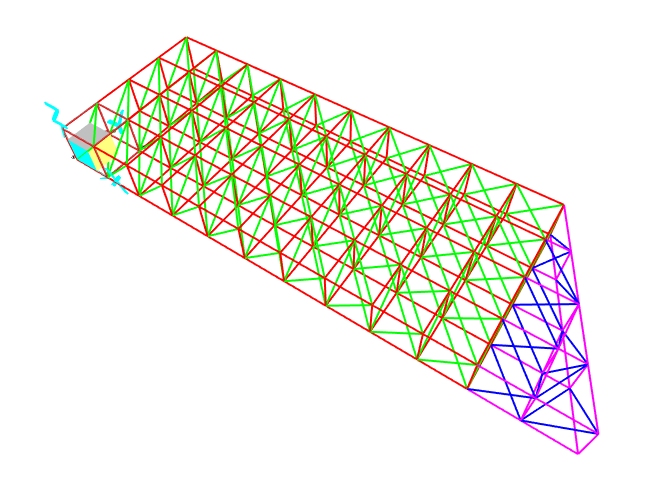
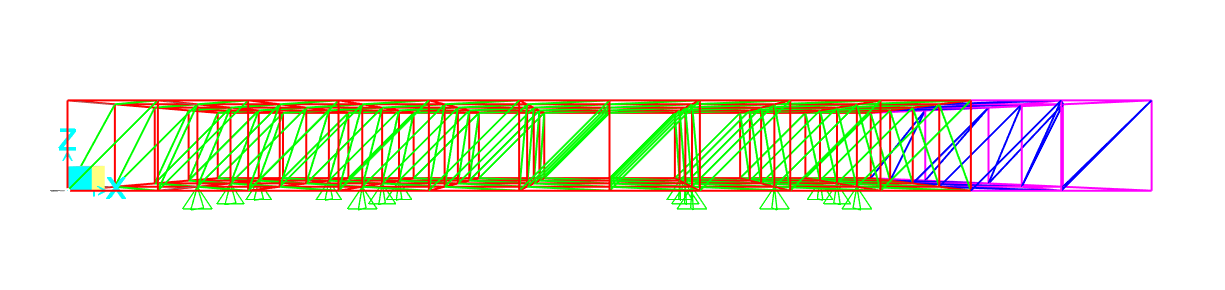
Procediamo con il dimensionamento di una trave reticolare spaziale, che tramite i pilastri appesi, porta i quattro piani che compongono l’edificio. I solai che costituiscono i piani dell'edificio sono in laterocemento con destinazione d'uso di abitazione civile. 

 

FASE1:

Analisi dei carichi di un solaio in laterocemento

1. Pavimentazione in ceramica
   2 cm = 0,02 m
2. Massetto
   4,00 cm = 0,04 m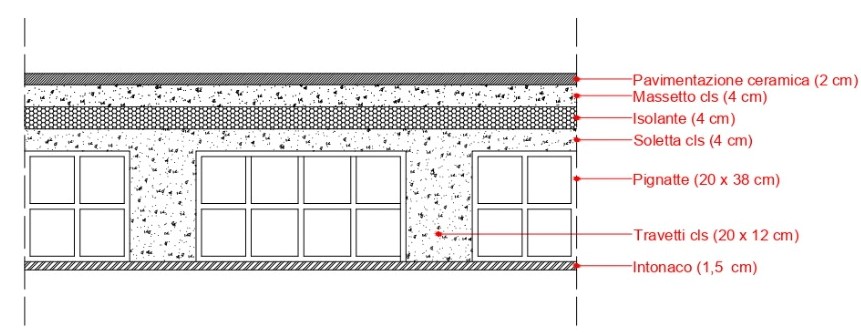
3. Isolante
   4,00 cm = 0,04 m
4. Soletta collaborante
   4,00 cm = 0,04 m
5. Pignatte
   20,00 cm = 0,20 m
6. Travetti
   20,00 cm = 0,20 m
7. Intonaco
   1,50 cm = 0,015 m

​Spessore totale solaio = 35,50 cm = 0,355 m

 

Calcolo del carico distribuito superficiale

1. Pavimentazione in ceramica = 0,40 KN/m²
2. Massetto = 0,76 KN/m²
3. Isolante = 0,008 KN/m²
4. Soletta = 1,00 KN/m²
5. Pignatte = 0,76 KN/m²
6. Travetti = 1,20 KN/m²
7. Intonaco = 0,30 KN/m²

 

- Carico strutturale q_s

   Soletta + Travetti + Pignatte

   1,00 KN/m² + 1,20 KN/m² + 0,76 KN/m² = 2,96 KN/m²

- Sovraccarico permanente q_p

   P. Ceramica + Massetto + Isolante + Intonaco + Incidenza impianti* + Incidenza tramezzi*

   0,40 KN/m² + 0,76 KN/m² + 0,008 KN/m² + 0,30 KN/m² + 0,50 KN/m² + 1,00 KN/m² =  2,97 KN/m²

^{*I valori sono stati scelti seguendo la NTC 2018}

- Carico accidentale q_a

Secondo NTC 2018, il valore relativo ad ambienti ad uso residenziale è pari a 2,00 KN/m²

Sono state considerate le combinazioni di carico fornite dalla NTC 2018 relative alle verifiche agli stati limite, utilizzando coefficienti parziali di sicurezza sfavorevoli.

Combinazione di carico allo stato limite ultimo SLU

γs qs + γp qp + γa qa = 1,30 x 2,96 KN/m² + 1,50 x 2,97 KN/m² + 1,50 x 2,00 KN/m² = 11,30 KN/m²

q_u = 11,30 KN/m²

 

Modello SAP 2000:

Partiamo con l'impostazione del modello attraverso la griglia

1. File > New Model > Grid only > 3x3x3

Si assegnano un materiale e una sezione iniziale ipotetica alle aste e alle aste diagonali

1. Define > Materials > Add new material > S355
2. Define > Section Properties > Frame Sections > Pipe > TUBO-D244.5 x 5.4 (Aste)
3. Define > Section Properties > Frame Sections > Pipe > TUBO-D273 x 5.6 (Aste diagonali)

Si definisce la posizione degli appoggi e le condizioni di vincolo fra le aste (il momento deve essere nullo).

1. Seleziono i nodi interessati > Assign > Joint > Restraints > Vincoli di tipo cerniera
2. Selezione tutte le aste > Assign > Frame > Releases/Partial fixity

 

Definiamo una forza F:

Ovvero:

F₁ = 11,30 x 396 x 4 = 17899,2 KN

A questa Forza va aggiunto il Peso Proprio (PP) della travatura reticolare che si determina effettuando un’analisi considerando il peso proprio DEAD. In seguito, si analizza la tabella Excel.

1.      Display > Show Tables > Analysis Results > Joint Output > Joint Reactions

La nuova Forza sarà:

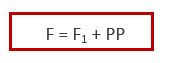
In seguito, si individuano le diverse aree di influenza e si calcola il numero dei nodi per ogni area

Aree regolari:

      Nodo centrale = 9 mq

      Nodo perimetrale = 4.5 mq

      Nodo angolare = 2.25 mq 

Aree irregolari:

1.         2.8125 mq 

2.         6.75 mq 

3.         2.25 mq

4.         8.7188 mq 

5.         4.7812 mq

6.         4.2187 mq 

7.         1.9688 mq

Sull'area rettangolare abbiamo:

     2 nodi angolari

     21 nodi perimetrali

     27 nodi centrali

Sull'area trapezoidale abbiamo:

     1 nodi centrali

     1 nodi perimetrali

     9 nodi misti: 1,2,2,3,3,4,5,6,7

 

Ora definiamo una nuova combinazione di carichi:

1.      Define > Load pattern > F > Add new load pattern

E si assegnano i carichi concentrati per ogni tipologia di nodo:

2.      - Nodi centrali > Assign > Joint loads > Forces > F = 317.64  kN

3.      - Nodi perimetrali > Assign > Joint loads > Forces > F = 158.82 kN

4.      - Nodi d’angolo > Assign > Joint loads > Forces > F = 79.41 kN

5.      - Nodi speciali > Assign > Joint loads > Forces > F = 

        1.         2.8125 mq x 35.29 = 99.26 KN

        2.         6.75 mq x 35.29 = 238.23 KN

        3.         2.25 mq x 35.29 = 79.41 KN

        4.         8.7188 mq x 35.29 = 307.71 KN

        5.         4.7812 mq x 35.29= 168.74 KN

        6.         4.2187 mq x 35.29 = 148.89 KN

        7.         1.9688 mq x 35.29 = 69.48 KN

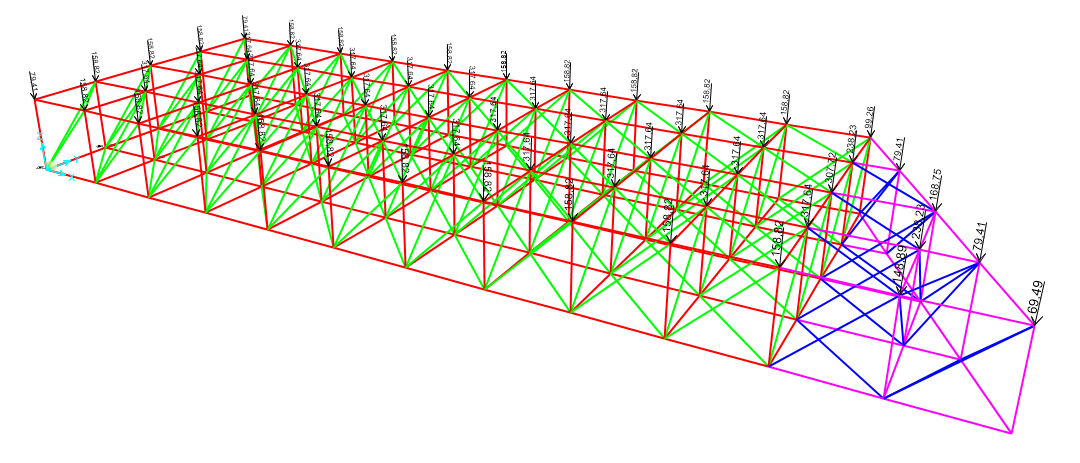
Ora definiamo una nuova combinazione di carichi:

1.      Define > Load pattern > SLE > Add new load pattern

E assegniamo i carichi concentrati al 70% (SLE) ad ogni tipologia di nodo, in modo da verificare la deformabilità degli sbalzi (abbassamento)

1.      - Nodi centrali > Assign > Joint loads > Forces > F = 222.35 KN

2.      - Nodi perimetrali > Assign > Joint loads > Forces > F = 111.17 KN

3.      - Nodi d’angolo > Assign > Joint loads > Forces > F = 55.59 KN

4.      - Nodi speciali > Assign > Joint loads > Forces > F =

        1.         69.48 KN

        2.         166.76 KN

        3.         55.59 KN

        4.         215.40 KN

        5.         118.12 KN

        6.         104.22 KN

        7.         48.64 KN

Ora avviamo l’analisi e verifichiamo l’abbassamento con SAP:

1.      Display Deformed Shape > SLE

Estraiamo le tabelle per verificare l’abbassamento allo SLE

1.      Display > Show Tables >

2.      Select Load Patterns > SLE

3.      Select Load Cases > SLE

Prendo la tabella relativa al Joint Displacement e verifico quali nodi presentano l’abbassamento maggiore (in relazione ad  1/200esimo  della luce)

Verifico dal modello SAP la distanza tra i nodi in questione e gli appoggi più vicini ad essi

1.      Select > Select Labels >

2.      Object Type > Joints

3.      Object Label > “numero nodo con abbassamento maggiore” (in questo caso: 267-288)

Applico la formula della Verifica di deformabilità:

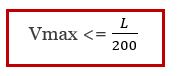
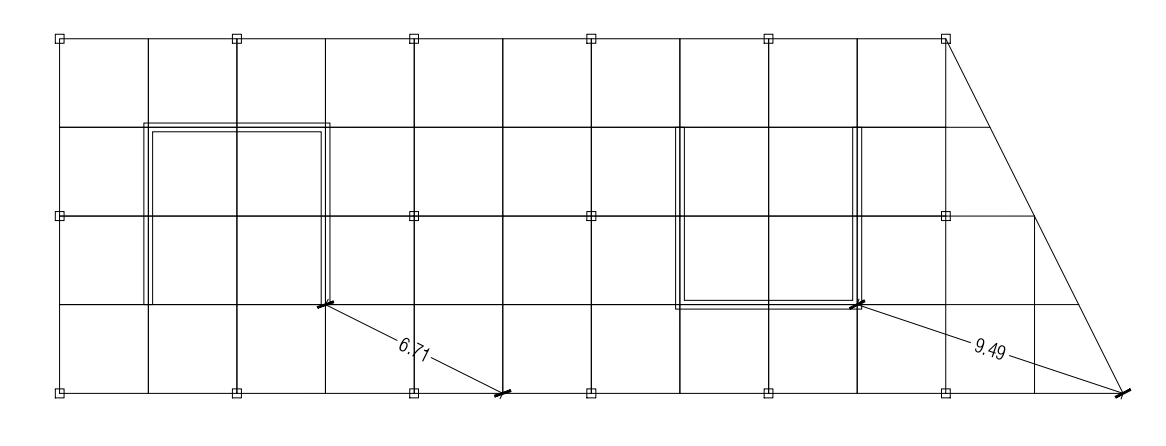
Calcolo la distanza nodo angolare (CAD) = 9.49 m

9.49 / 200 = 0.05 m      (1/200esimo della luce)

0.018 < 0.05                   Verifica soddisfatta

 

Calcolo la distanza nodo angolare (CAD) = 6.71 m

6.71 / 200 = 0.04 m      (1/200esimo della luce)

0.008 < 0.04                   Verifica soddisfatta

 

Ora estraiamo le tabelle per dimensionare le aste

1.      Display > Show Tables >

2.      Select Load Patterns > F

3.      Select Load Cases > F

Prendo le tabelle relative a Element Forces - Frames e ordino i valori delle sollecitazioni in base allo sforzo normale di trazione e compressione

Scegliamo gli intervalli di sollecitazioni per le assegnazioni delle sezioni:

SEZ A  (1000- 600 KN)

SEZ B   (600- 400 KN)

SEZ C  (400- 200 KN)

SEZ D  (200- 100 KN)

SEZ E  (100- 40 KN)

SEZ F  (40- 0 KN)

SEZ G  (0- 100 KN)

SEZ H  (100- 300 KN)

SEZ I  (300- 600 KN)

 

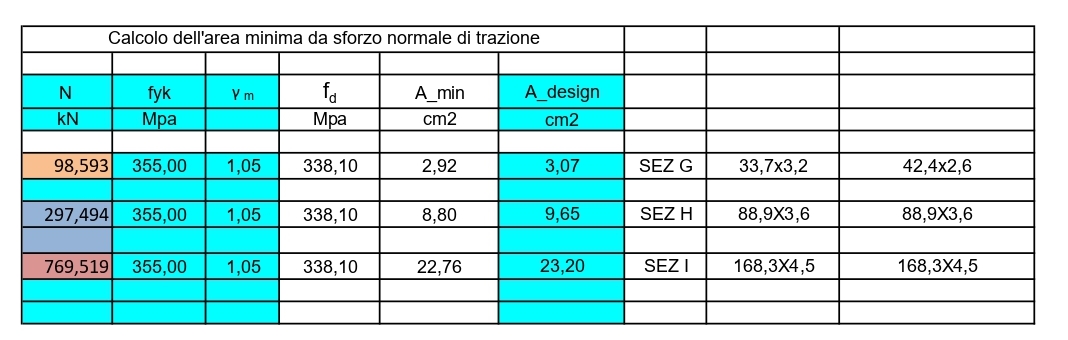
Dimensioniamo le aste a trazione e compressione mediante le tabelle Excel:

Dopo aver diviso in gruppi le sezioni ,da A ad I,e assegnato per ciascuna una dimensione a seguito del predimensionamento fatto tramite Excel, reinseriamoi valori ottenuti attraverso le tabelle di Sap all’interno del programma steso così da consentire a quest ultimo di associare ad ogni valore trovato per lo Sforzo Normale, la rispettiva sezione.

 

Aste a compressione

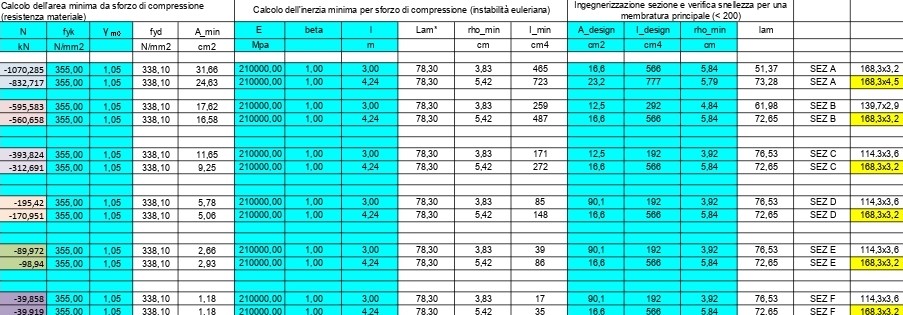
Aste a trazione

 

Ora, scelte le sezioni adeguate, inseriamo nelle varie tabelle esportate da SAP l'informazione che ne modificherà le sezioni precedentemente assegnate:

File > Import > Sap 2000 MS Excel Spreadsheet .xls File > add to existing model > ok

Overwrite previous - Replace element in model- Replace item in model

 

FASE 2:

Ora definiamo le nuove combinazioni di carichi che comprendano il nuovo peso proprio definito dalle nuove sezioni delle aste:

Per prima cosa assegniamo i carichi concentrati al 70% (SLE) ad ogni tipologia di nodo, in modo da verificare la deformabilità degli sbalzi (abbassamento)

      Define > Load pattern > SLE₂ > Add new load pattern

Ora ripetiamo l’analisi e verifichiamo nuovamente l’abbassamento con SAP:

1.      Display Deformed Shape > SLE₂

Estraiamo le tabelle per verificare l’abbassamento allo SLE

1.      Display > Show Tables >

2.      Select Load Patterns > SLE

3.      Select Load Cases > SLE

Prendo la tabella relativa al Joint Displacement e verifico quali nodi presentano l’abbassamento maggiore (in relazione ad  1/200esimo  della luce)

Verifico dal modello SAP la distanza tra i nodi in questione e gli appoggi più vicini ad essi

1.      Select > Select Labels >

2.      Object Type > Joints

3.      Object Label > “numero nodo con abbassamento maggiore” (in questo caso: 267-288)

Applico la formula della Verifica di deformabilità:

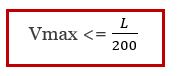
Calcolo la distanza nodo angolare (CAD) = 9.49 m

9.49 / 200 = 0.05 m      (1/200esimo della luce)

0.12 < 0.05                   Verifica non soddisfatta

 

Calcolo la distanza nodo angolare (CAD) = 6.71 m

6.71 / 200 = 0.04 m      (1/200esimo della luce)

0.05 < 0.04                   Verifica non soddisfatta

 

Non essendo soddisfatta la verifica all’abbassamento, aumentiamo la sezione delle aste

SEZ A (219.1 x 5.0)

SEZ B (219.1 x 4.0)

SEZ C (219.1 x 4.0)

SEZ D (219.1 x 4.0)

SEZ E (219.1 x 4.0)

SEZ F (219.1 x 4.0)

SEZ G (42.4 x 2.6)

SEZ H (88.9 x 3.6)

SEZ I (168.3 x 4.5)

E ridefiniamo nuovamente le nuove combinazioni di carichi che comprendano il nuovo peso proprio definito dalle nuove sezioni delle aste:

Assegniamo i carichi concentrati al 70% (SLE) ad ogni tipologia di nodo, e riverifichiamo la deformabilità degli sbalzi (abbassamento)

Applichiamo nuovamente la formula della Verifica di deformabilità:

9.49 / 200 = 0.05 m      (1/200esimo della luce)

0.10 < 0.05                   Verifica non soddisfatta

 

6.71 / 200 = 0.04 m      (1/200esimo della luce)

0.03 < 0.04                   Verifica soddisfatta

 

Non essendo soddisfatta la verifica relativa ai nodi (267-288), si è proceduto con l’inserimento di un ulteriore sostegno.

Applico ancora una volta la formula della Verifica di deformabilità:

Calcolo la nuova distanza del sostegno dal nodo angolare (CAD) = 4.28 m

4.28 / 200 = 0.021 m      (1/200esimo della luce)

0.01 < 0.021                 Verifica soddisfatta

 

Poi si assegnano i carichi concentrati (SLU) per ogni tipologia di nodo:

           Define > Load pattern > F₂ > Add new load pattern

1.      - Nodi centrali > Assign > Joint loads > Forces > F = 307.98  kN

2.      - Nodi perimetrali > Assign > Joint loads > Forces > F = 153.99  kN

3.      - Nodi d’angolo > Assign > Joint loads > Forces > F = 76.995 kN

4.      - Nodi speciali > Assign > Joint loads > Forces > F = 

        1.         2.8125 mq x 34.22 = 96.24 KN

        2.         6.75 mq x 34.22  = 230.985 KN

        3.         2.25 mq x 34.22 = 76.995 KN

        4.         8.7188 mq x 34.22 = 298.357 KN

        5.         4.7812 mq x 34.22 = 163.613 KN

        6.         4.2187 mq x 34.22 = 146.70 KN

        7.         1.9688 mq x 34.22 = 67.37 KN

Per la verifica delle aste si procede poi con l’avvio dell’analisi su SAP e la successiva estrazione delle tabelle delle sollecitazioni delle aste. 

Poi inseriamo i nuovi valori all'interno della tabella Excel e si procede nuovamente con la verifica al dimensionamento.

Aste a compressione

Aste a trazione

Verifiche al dimensionamento soddisfatte

 

 

 

 

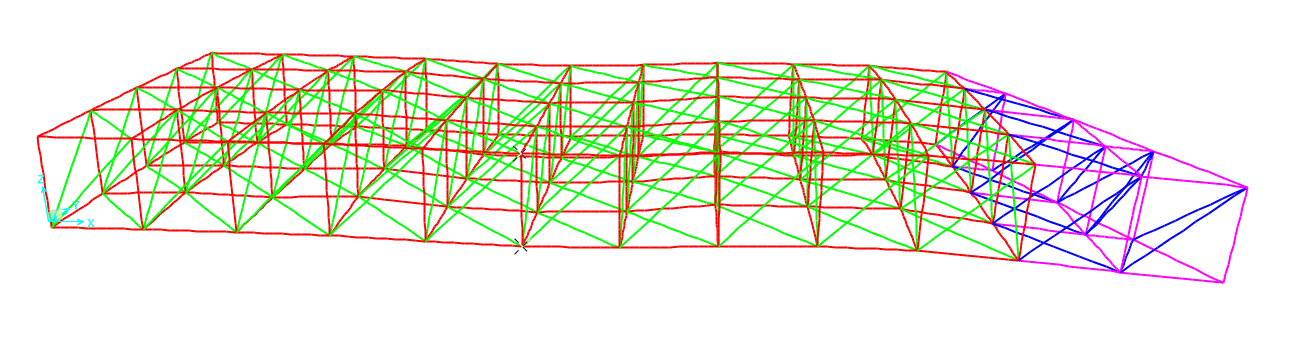
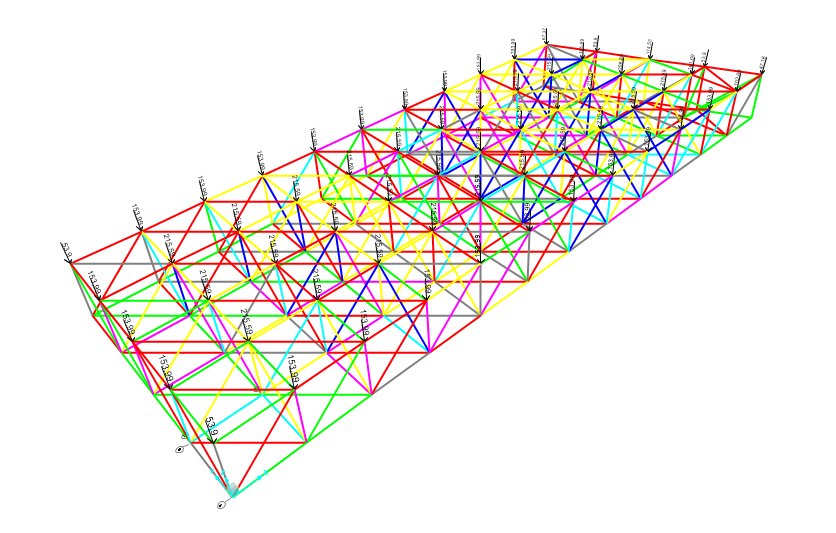
Render del modello di edificio appeso ad una travatura reticolare

Studenti: Jacopo Sforza, Brooke Sison, Andrea Spinaci

L’obiettivo dell’esercitazione è il progetto e il dimensionamento di una travatura reticolare 3D. La scelta di questa soluzione strutturale permette di avere ampie zone libere. Si è ipotizzata una struttura di 18m x 35m, con una parte irregolare (avente moduli 2,5m x 3m x 3m e una parte regolare composta da moduli di dimensioni 3m x 3m x 3m).

Definito l’impianto, è stato ridisegnato all’interno dell software SAP2000 partendo dalla costruzione di un modulo di 3 m x 3m x 3m lungo i tre assi X, Y, Z. All’interno del modulo di base abbiamo assegnato i diversi frame strutturali: aste verticali, orizzontali e diagonali con un profilo tubolare di D323,9 x 7,1 mm. Come materiale è stato scelto l’acciaio S355. 

Per completare la parte regolare della struttura è stato utilizzato il comando replicate ctrl+r, mentre la parte irregolare è stata costruita attraverso il comando punto (offset lungo gli assi x,y,z) e la costruzione delle singole aste. Ogni frame è stato assegnato al relativo gruppo (con le diverse proprietà): aste e diagonali triangolari, aste e diagonali irregolari.

Successivamente sono stati attribuiti i vincoli. Visto che le aste di una struttura reticolare sono tra loro incernierate, è stato definito il vincolo di cerniera tra tutte le aste attraverso il comando assign > frame > release/partial fixities. Inoltre sono stati definiti i vincoli cerniera nei punti in cui sono state progettate le strutture verticali definite dai pilastri e setti attraverso il comando assign > joint restraint > vincolo cerniera.

Per la definizione dei carichi viene individuato il peso del solaio al mq utilizzato nella precedente esercitazione pari a 13,872 KN/mq con un numero di piani pari a 3. Il peso del solaio che la struttura reticolare dovrà sostenere sarà pari a 13,872 KN/mq x 3 = 41,616 KN/mq. Per quanto riguarda il peso proprio della struttura reticolare è stato calcolato attraverso sap2000 sommando i diversi contributi F3 delle reazioni vincolari attraverso il comando run analisys > modal > run now – tabella Joint Reactions.

Valore del peso proprio: 1446,03 KN/mq
Area = (18 x 30) + (5 x 18/2) = 540 + 45 = 585 mq
F = (13,872  x 585) x (n=3)= 24.345,36 KN
Ftot = 25.791,39 KN

Successivamente abbiamo individuato il numero di nodi:

Nc= 52; Np= 30; Na= 4

Ftot= 52F + 30/2F + 4 F/4
Fnodo= 25.791,39 KN /68= 379,28 KN

Fc= 379,28 KN; Fp= 189,64 KN; Fa= 94,82 KN

In seguito è stata fatta l'analisi su Sap2000 verificando i punti di abbassamento massimo Vmax:

Nodo 145: L= 8,37 /250 = 0,033   Vmax = 0,016  La verifica di abbassamento nel nodo con Vmax viene rispettata.

DIVISIONE DELLE SEZIONI

Abbiamo diviso la struttura in tre gruppi: 

-        Struttura regolare

-        Struttura aste irregolari

-        Struttura diagonali irregolari

Per ogni singolo gruppo è stato esportato su Excel: Frame Section Assignment e Element forces frames. Per la Tabella Element forces Frame abbiamo assegnato gruppi di sezioni a seconda dello sforzo di trazione e di compressione.

Successivamente è stata utilizzata la Tabella Acciaio Aste Reticolare per il dimensionamento degli elementi, utilizzando la sollecitazione massima per ogni sezione.

Dopodiché sono state assegnate le sezioni sulla tabella Frame Section Assignment.

Nel momento di assegnazione delle sezioni su SAP2000, per la parte della struttura regolare, per ogni gruppo di aste e diagonali, abbiamo scelto le sezioni aventi l'area maggiore tra le aste e le diagonali più sollecitate.
Successivamente al dimensionamento, nella verifica è stata considerata la sezione maggiore tra il gruppo di aste e diagonali. 

Per la parte della struttura ad aste regolari i frame sono dalla SEZ. A a SEZ. I , per la parte delle aste irregolare dalla SEZ. L a SEZ. O. mentre per le diagonali dalla SEZ. P alla SEZ. T. Infine per ogni gruppo è stata importata la Tabella Excel per definire le varie sezioni su Sap2000.

Dopo aver assegnato le nuove sezioni, è stato ricalcolato il Peso Proprio della Struttura reticolare attraverso la somma delle Reazioni Vincolari.

Nuovo valore del peso proprio della struttura reticolare: 342,04 KN/mq

Ftot= 52F + 30/2 F+ 4/4F

Ftot = 24.345,36 + 342,04 = 24.687,4 KN
Fnodo= 24.687,4/68= 363,05 KN
Fc= 363,05 KN; Fp= 181,53 KN; Fa= 90,76 KN

Per quanto riguarda l'abbassamento viene fatta di nuovo l’analisi con l'esportazione su Excel delle tabelle Frame Section Assignment e Element forces frames e viene controllato che le nuove sezioni siano verificate.

TABELLA CON VERIFICA GRUPPO STRUTTURA NON REGOLARE ASTE (COMPRESSIONE E TRAZIONE)

TABELLA CON VERIFICA GRUPPO STRUTTURA REGOLARE (COMPRESSIONE E TRAZIONE)

TABELLA CON VERIFICA GRUPPO STRUTTURA NON REGOLARE DIAGONALI (COMPRESSIONE E TRAZIONE)

In allegato le tabelle con il dimensionamento e la verifica secondo le diverse sezioni assegnate. 

 

Trave reticolare con modulo (3X3) di Area 1400mq a cui sono appesi 3 solai della stessa area. Considerando il peso al mq del solaio di 10 kn/mq risulta un peso dei solai complessivo di 42000 kn da ridistribuire per ogni nodo.A questo peso poi occorrerà aggiungere il peso proprio della travatura reticolare.

 

 

Calcolo peso proprio trave con sezioni provvisorie poi aggiunto al peso totale dei solai.

 

Ora si prosegue calcolando l'abbassamento massimo allo SLE, che abbiamo considerato pari a 3/4 del valore dello SLU

Andando a prendere il valore massimo.

Calcolo della distanza minima dell'abbassamento dal vincolo più vicino.

Una volta verificato l'abbassamento si procede con la verifica alla resistenza con lo SLU.

Dopo aver avviato l'analisi allo SLU si espertano le tabelle di tutte le aste verticali, orizzontali e diagonali con i loro sforzi assiali.

Dividendo poi le aste per grandezza dello sforzo normale in vari gruppi da cui ne dipendono le sezioni. (Gruppo A-B-C-D-E-F Compressione, Gruppo G-H-I-L-M Trazione)

Mettiamo in relazione la divisione precedentemente fatta per le aste e le diagonali con la nuova suddivisione da esportare su SAP.

Si prendono i valori massimi di ogni gruppo per dimensionarli a pressoflessione per le aste compresse considerando anche la lunghezza dell'asta.

Mentre per le aste tese ci limitiamo a dimensionare in base all'area minima.

Una volta esportato il file exel lo si importa su sap così da cambiare le sezioni precedenti con quelle appena dimensionate.

Per la vonferma ulteriore della travereticolare bisogna ricalcolare il peso proprio della struttura sulla base delle nuove sezioni.

La trave risulta più leggera e anche meno rigida quindi si ricalcola l'abbassamento massimo allo SLE ricalcolato.U3 risultà più grande rispetto a prima superando i limiti di normativa, per questo al fine di diminuire la distanza minima andremo ad aggiungere un vincolo in prossimità del nodo numero 206.

Ricalcolo del peso agente su ogni nodo, risultando minore a prima si conviene che l'unica azione da fare è aggiungere un vincolo. Le aste e le diagonali per prime progettate erano sovradimensionate.

 

 

quindi, alla F_TOT, viene aggiunto il Peso Proprio

 

Questo è tutto il peso portato dalla trave reticolare, che deve essere ridistribuito sui nodi.

Quindi, vengono calcolati quanti sono i nodi centrali, perimetrali e angolari.

N_C = 180

N_P = 58

N_A = 4

Nei nodi, la forza sarà moltiplicata per l’area di influenza. Quindi, se nel nodo centrale viene applicata una forza F, nei nodi perimetrali una forza F/2  mentre in quelli angolari una forza F/4.

Di conseguenza:

Quindi, la forza da applicare al nodo sarà:

307 kN è la forza massima.

Quindi ai nodi centrali vengono assegnati i 307 kN; ai nodi perimetrali viene applicata la forza moltiplicata per 1/2 , mentre ai nodi angolari viene applicata la forza moltiplicata per 1/4.

Quindi F_P = 153,5 kN e F_A = 76,75 kN.

(Per verificare l’abbassamento, è necessario lo stato limite d’esercizio, perché la verifica dell’abbassamento si fa con lo SLE.)

Assegnato il carico e le sezioni, viene fatta partire una nuova analisi in cui viene analizzato solo il caso F e vengono analizzate le tabelle “Joint Displacement”, cioè lo spostamento dei punti.

L’abbassamento massimo si trova nel nodo n.41.

L’abbassamento massimo non deve essere superiore a 1/200 della luce.

La luce sarà uguale alla distanza del punto di massimo abbassamento dal vincolo più vicino.

Il nodo 41 dista di 4 moduli lungo l’asse x e di 2 moduli lungo l’asse y dalla cerniera più vicina.

Quindi

Una volta verificato l’abbassamento, viene esportata la tabella “Element Forces Frame” dove si trovano i risultati in termini di taglio, momento e sforzo normale delle aste verticali e orizzontali e delle aste diagonali; e la tabella “Frame Assignments”, che è una tabella in cui vengono ricapitolati il numero del frame e il tipo di aste, se diagonale o orizzontale e verticale.

Si procede con il raggruppamento degli elementi compressi in cinque gruppi e vengono considerati per ogni gruppo l’elemento con maggiore kN. 

Successivamente si deve verificare se le sezioni delle varie aste possano andare bene, altrimenti viene data una nuova sezione con l’ausilio del sagomario.

Quindi, per il primo raggruppamento, viene presa l’asta con sforzo normale maggiore e viene verificata. Stesso procedimento viene fatto per gli altri raggruppamenti.

 

 

 

 

 

CALCOLO DELL’AREA MINIMA DA SFORZO DI COMPRESSIONE

Stessa verifica viene fatta per la trazione, quindi:

CALCOLO DELL’AREA MINIMA DA SFORZO DI TRAZIONE

 

Questi valori devono essere importati su SAP2000.

Quindi, su SAP2000 vengono ridefinite le sezioni e successivamente viene importata la tabella.

 

TRAVE RETICOLARE CON LE SEZIONI NUOVE IMPORTATE DA EXCEL

Successivamente, viene rifatta l’analisi solo con il peso proprio, per ottenere il nuovo peso della trave; il valore di peso proprio viene aggiunto all’analisi dei carichi che rimane invariata perché si parla dei carichi appesi alla trave reticolare. Quindi, vengono calcolate di nuovo le forze da applicare sui singoli nodi e viene fatta una nuova analisi. Infine, vengono analizzate tutte le nuove tabelle e viene controllato che siano tutte quante verificate.

 

Questo è tutto il peso portato dalla trave reticolare, che deve essere ridistribuito sui nodi.

Nei nodi, la forza sarà moltiplicata per l’area di influenza. Quindi, se nel nodo centrale viene applicata una forza F, nei nodi perimetrali una forza F/2 mentre in quelli angolari una forza F/4.

Di conseguenza

Quindi, la forza da applicare al nodo sarà:

291,9 kN è la forza massima.

Ai nodi centrali saranno assegnati i 291,9 kN.

Ai nodi perimetrali sarà assegnata la forza moltiplicata per 1/2, mentre ai nodi angolari sarà applicata la forza moltiplicata per 1/4.

Quindi F_P = 145,95 kN e F_A = 72,97 kN.

Successivamente queste forze vengono di nuovo assegnate ai nodi; viene fatta di nuovo l’analisi e viene controllato che nuove sezioni siano verificate.

DEFORMATA LUNGO L’ASSE xz

Vengono estrapolate le tabelle “Element Forces Frame” e “Frame Section Assignment”, vengono riportati tutti i gruppi e viene fatta la verifica finale.

CALCOLO DELL’AREA MINIMA DA SFORZO DI COMPRESSIONE

CALCOLO DELL’AREA MINIMA DA SFORZO DI TRAZIONE

Dall’analisi, due aste di due sezioni non risultano verificate, quindi, per queste aste, è necessario aumentare la sezione prendendo un momento di inerzia e un raggio maggiore.