Portale di Meccanica

Questo è il mio primo blog

Laboratorio di progettazione strutturale 1M

Prof: Ginevra Salerno, Prof: Fabiana Riparbelli

A. A. 2020 - 2021

Studenti: Patryk Rynkowski, Luca Santilli

 

 

 

 

 

 

 

 

 

 

Il progetto si propone di risolvere l'importante snodo urbano tra via Ostiense e via del Porto Fluviale con un edificio a destinazione d'uso mista: commerciale ed uffici. La prima si troverà principalmente ai piani terra e primo, mentre la seconda andrà a svilupparsi in altezza nei piani superiori dei corpi di fabbrica. 

Le strutture sono risolte per la maggior parte con l'utilizzo di telai in calcestruzzo armato, con pilastri che poggiano a terra dal piano interrato dei parcheggi. Elemento fondante del progetto è però una piazza aperta interna, che servirà ad unire le dimensioni pubbliche a quelle private, e che configurerà il progetto con una corte interna. Tale piazza sarà raggiungibile da più direzioni esterne tramite dei grandi passaggi permeabili ottenuti grazie all'apertura del corpo di fabbrica su via Ostiense.

La soluzione strutturale che ha reso possibile questa connessione tra interno ed esterno è quella del graticcio, sorretto da due coppie di grandi pilastri ortogonali tra loro e uno centrale, che formerà un accesso dall'incrocio con le due importanti vie. Superiormente al graticcio si trova un telaio in calcestruzzo armato, il quale poggia i propri pilastri sui nodi. 

In tutti i corpi di fabbrica del progetto la maglia strutturale dei telai ha sempre una configurazione interna, il che lascia spazio al disegno di facciate libere, continue.

Gruppo: Panella Giordana e Ilaria Quagliani

Il progetto è situato a Roma in un lotto trapezoidale delimitato su due lati da via Ostiense e via del Porto Fluviale, a nord dalla ferrovia e ad ovest da una preesistenza.

L'edificio si articola su 8 piani:

• 2 piani interrati, dove troviamo un piano di parcheggi e la prima parte di zona commerciale
• piano terra dedicato ad altri servizi per il pubblico
• primo piano adibito ai servizi per gli uffici (reception, mensa...)
• 4 piani di uffici

I primi quattro piani sono strutturalmente sorretti da un telaio in cemento armato e gli altri 4 da una reticolare spaziale in modo da creare una grande terrazza pensata per rendere più piacevole la pausa pranzo degli impiegati. Inoltre questo tipo di struttura ci ha permesso di svuotare l'angolo all'incrocio di Via Ostiense e Via del Porto Fluviale in modo da alleggerire il fronte stradale già saturo nel quartiere.

La reticolare è sorretta da tre vani in cemento armato posizionati appositamente in modo da bilanciare tutta la struttura. Essi sono giuntati dal telaio in modo da non compromettere la staticità dell'edificio.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Per questa esercitazione abbiamo dimensionato un graticcio di travi inflesse partendo da un modello idealizzato di piastra, effettuando un infittimento delle travi. La piastra presenta un comportamento, fuori dal piano medio, soggetto prevalentemente a momento flettente M.

Momenti intorno a x e y.

Tagli che equilibrano la forza F.

Il graticcio è un oggetto tridimensioanle rappresentato da un modello bidimensionale dove i momenti abitano su due piani diversi per questo nell'equilibrio rotazionale si sommano i momenti Mx e My separatamente.

Rotazione e curvatura intorno a X

 

Rotazione e curvatura intorno a Y

GEOMETRIA

Abbiamo scelto una piastra di dimensioni 30 x 30 m con appoggi ogni 10 metri in modo da avere 4 appoggi per lato. a questo abbiamo diffrerenziato i pilastri per sezioni:

PILASTRI ANGOLARI: 100 x100 cm:

PILASTRI DI BORDO: 120 x 60 cm 

come prima cosa, avendo dimensionato sezioni rettangolari per i pilastri di bordo si dovrà tener conto dell’orientamentamento e quindi del valore del momento di inerzia che inciderà sulla rigidezza. Si è provveduto a ruotare i pilastri perimetrali posti lungo l’asse Y ( sistema globale ) andando a ruotare di 90° gli assi locali degli elementi. In questo modo il momento d’inerzia aumenta in quanto la base e l’altezza sono invertite e di conseguenza maggiore sarà la rigidezza.

Una volta assegnate le sezioni ai pilastri definiamo la sezione della piastra con shell-thick e imposto un’altezza di 100 cm. Per simulare il comportamento di un sistema discreto definisco un materiale C50/60 fittizio ponendo il coefficiente di poisson pari a 0 in quanto sappiamo che nel graticcio le deformazioni laterali delle travi sono trascurabili rispetto alle deformazioni principali.

Sistema continuo; Sistema discontinuo

ASSEGNAZIONE DEI CARICHI

Dopo aver discretizzato l’area suddivido i nodi dell piastra per l’assegnazione dei carichi verticali:

NODI CENTRALI

NODI PERIMETRALI

NODI ANGOLARI

L’edificio ipotizzato ha una struttura che regge 4 piani. Ogni piano occupa una superficie di 900 mq. Devo calcolare il carico di stato ultimo qu facendo l’analisi dei carichi del solaio. Scelgo un solaio in acciaio con qu di 12,45 KN/m2 . Per ogni nodo viene considerata l’area di influenza, dove per i perimetrali l’area di influenza è la metà e per gli angolari è 1/4 mentre per quelli centrali è massima.

P solaio= n x qu x A = 4 x 12,45 KN/m2 x 900 m2 = 44820 KN 

Nodi totali - nodi perimetrali - nodi angolari = Nodi centrali = 3600

Fc= 44820 KN / 3600 = 12,45 KN

Fp= 12,45 KN / 2 = 6,22 KN

Fa= 6,22 KN / 2= 3,11 KN

Assegno le forze ai nodi e mando l’analisi con il carico definito allo SLU e con il fattore moltiplicativo a 1 per considerare il peso proprio della struttura. Dai diagrammi del momento flettente i valori di m 1-1 e m 2-2 sono gli stessi valori, in quanto il sistema è simmetrico. Prendiamo il valore massimo in corrispondenza di un pilastro per dimensionare l’altezza della piastra.

 

 

 

 

 

 

DISEGNO RETICOLO GRATICCIO

Per dimensionare l’altezza delle travi del graticcio abbiamo calcolato il momento di inerzia di una porzione di piastra considerando l’interasse delle travi quindi in base a quante travi posiziono lungo i lati. Le travi dovranno avere lo stesso lo stesso momento di inerzia della porzione di piastra ma con base un base diversa e l’altezza mi dovrà garantire lo stesso valore di I e quindi l’incognita è h3.

h = (12 Ix / b) 1/3

La sezione della trave da assegnare nel modello di SAP è 40 cm x 190 cm. A questo punto modello il reticolo di travi inflesse andando a definire le sezioni ottenute. Per simulare un nodo rigido interno separo le travi modellate in modo che non siano continue.

 

Vado ad assegnare le forze concentrate in corrispondenza dei nodi centrali, perimetrali e angolari considerando le relative aree di influenza.

Fc= 44820 m2 / 144 = 311,25 KN

Fp= 155,63 KN

Fa= 77,81 KN

Definisco un nuovo carico Q con fattore moltiplicativo pari ad 1 sempre per considerare il peso effettivo della struttura e mando l’analisi per effettura la verifica di resistenza degli elementi e verificare allo SLE gli abbassamenti.

VERIFICA DI RESISTENZA TRAVI

Confrontando i valori dei momenti, in corrispondenza del nodo rigido tra trave e appoggio notiamo che sono molto simili.

Mmax (trave) = 11343,30KNm

Mmax (pilastro) = 11935,94 KNm

 

Diagrammi dei momenti M3 travi e pilastri

Per evitare che le travi si deformino troppo possiamo aumentare la rigidezza torsionale della trave di bordo, in questo modo, parte del momento flettente che arriva al nodo sarà assorbito dalla trave di bordo irrigidita aumentando la base. Assegnata la nuova sezione alla trave di bordo di 100 x 190 cm rimandiamo l’analisi per verificare i momenti sulle travi del graticcio. Dato che i contributi dei momenti delle travi, che appoggiano sulla trave di bordo e sugli appoggi scaricheranno sui pilastri, quest’ultimi risulteranno molto sollecitati. Dimensiono la sezione dei pilastri con il momento massimo 11351,11 KNm.

la sezione da assegnare ai pilastri è 60 x 190 cm. A questo punto per dimensionare la sezione della trave del graticcio rimando l’analisi prendendo il nuovo valore del momento massimo uguale 11247,83 KNm.

L’altezza minima risulta essere 219,78 cm quindi posso prendere una sezione di 40 cm x 230 cm e la assegno su SAP. Rimandando nuovamente l’analisi, il valore del momento massimo risulta 11562,35 KNm.

La sezione 40 x 230 cm risulta soddisfatta per la verifica a resistenza.

VERIFICA A PRESSOFLESSIONE PILASTRI

A questo punto abbiamo verificato la sezione dei pilastri soggetti a pressoflessione con il valore del momento ottenuto dopo aver assegnato la sezione della trave di bordo. Possiamo notare dal diagramma dello sforzo normale che il graticcio si comporta come una serie di portali.

Diagrammi Sforzo normale

 Dalla verifica risulta non verificata la sezione 60 x 190 cm e quindi andremo ad aumentare la sezione ottenendo dei piccoli setti.

VERIFICA DEFORMABILITA'

Devo verificare di quanto si abbassi e per essere soddisfatta l’abbassamento maggiore non deve superare un 1/200 della distanza maggiore tra gli appoggi. Per verificare la deformabilità devo assegnare il carico allo stato limite d’esercizio. Prendo lo spostamento maggiore e verifico che sia minore di L/200, dove L è la distanza massima. Dalla deformata risulta che il valore massimo di abbassamento è di 2,6 cm che soddisfa la verifica di deformabilità.

L’obiettivo di questa esercitazione è il dimensionamento e la verifica di un graticcio di travi inflesse e dei pilastri su cui poggia.
 Per l'esercitazione è stata ipotizzata una struttura di 50 m x 30 m in pianta, sostenuta da pilastri con un interasse di 10 m. Il progetto prevede che il graticcio, sostenuto da 4 pilastri angolari di dimensioni 1m x 1m e 12 pilastri perimetrali di dimensioni 1,2m x 0,6m, sorregga sopra di sé ulteriori 3 piani. 

Disegnamo quindi la struttura su Sap2000 definendo le sezioni dei pilastri utilizzando una classe di cemento ad alte prestazioni C50/60. Controlliamo poi l’orientamento dei pilastri in modo da ottenere l’inerzia maggiore lungo la direzione dove avremo le travi del graticcio; assegniamo il vincolo d’incastro ai pilastri e successivamente per iniziare il dimensionamento del graticcio studiamo il comportamento di una piastra (Shell) in calcestruzzo.

Discretizziamo la superficie in elementi più piccoli di 0.50 m x 0.50m e assegnamo i carichi. Si assegna un carico distribuito indicativo di progetto pari a Qu= 10KN/m, ripartendo il carico come carico puntuale F nei nodi centrali, F/2 in quelli di bordo e F/4 negli angoli. Si procede poi con l'avvio dell'analisi del modello grazie alla quale si osserva l’abbassamento max nettamente minore di 1/200 della luce massima e un Mmax di 3171,57 KNm.
Dopo aver effettuato l'analisi iniziale, proseguiamo con la modellazione del graticcio e assegnamo i carichi concentrati sui nodi:
Nodi centrali: 188,28KN
Nodi perimetrali: 94,14KN
Nodi angolari: 47,07KN

Avviando ora l'analisi otteniamo i seguenti schemi:

Grafico della deformata:

Grafico degli sforzi assiali:

Grafico dei momenti:

Dimensionamento:

Dall'analisi di sap2000 abbiamo estrapolato i valori massimi dei momenti e degli sforzi assiali con i quali abbiamo predimansionato le sezioni delle travi e dei pilastri. 
L' abbassamento risulta soddisfatto; vediamo però che travi di bordo e pilastri (non quelli angolari) sono sottodimensionati. Andiamo perciò ad irrigidire la struttura aumentando le sezioni.
Come prima cosa dimensioniamo la trave di bordo dove vediamo che il momento massimo è di 16000 KNxm:

Portando la base della trave di bordo da 0,4m a 1m vediamo come il valore scende a 10000 KNxm:

Vediamo che i pilastri arrivano ad avere un momento massimo di 16500 KNxm, inseriamo il valore in excel:

L'altezza della sezione del nostro pilastro dovrà essere di almeno 217cm per sopportare questo sfrozo.Le sezioni iniziali non risultavano quindi verificate a presso-flessione, per questo motivo abbiamo svolto diverse iterazioni fino ad arrivare alla soluzione finale, che prevede le travi di bordo di dimensioni 1,8m x 1m, i pilastri perimetrali (non angolari) 2,2m x 0,6m e il graticcio 1,8m x 0,4m.

Notiamo in ultimo che l'abbassamento risulta ridotto a seguito dell'irrigidimento della struttura. 0,06<30/200

 

 

Laboratorio di Progettazione Strutturale 1M – Prof. Ginevra Salerno

Esercitazione 5: Dimensionamento di un graticcio di travi inflesse

Studenti: Patryk Rynkowski, Luca Santilli

L’obiettivo di questa esercitazione è quello di dimensionare, partendo da una piastra, un graticcio di travi inflesse estrapolato dal caso di studio del nostro progetto.

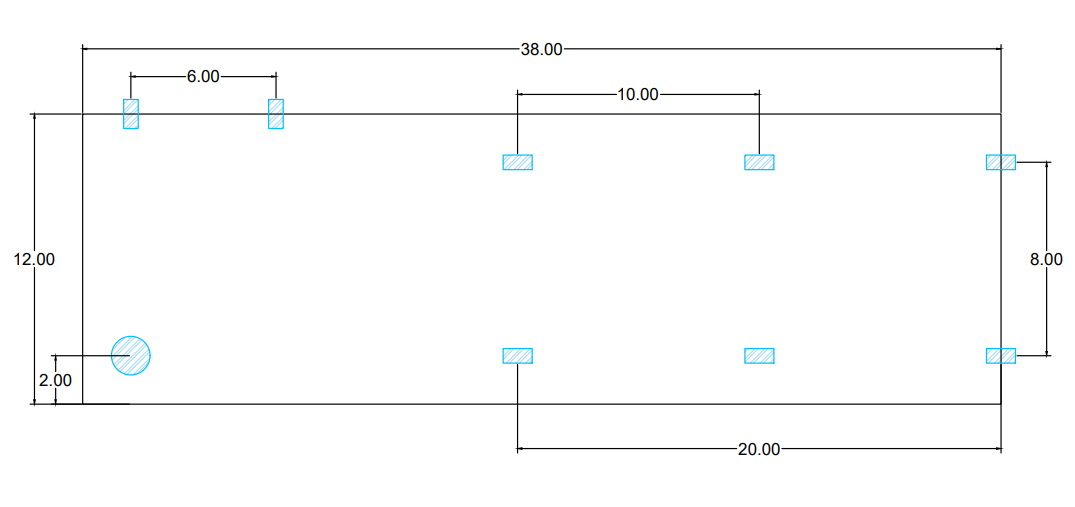
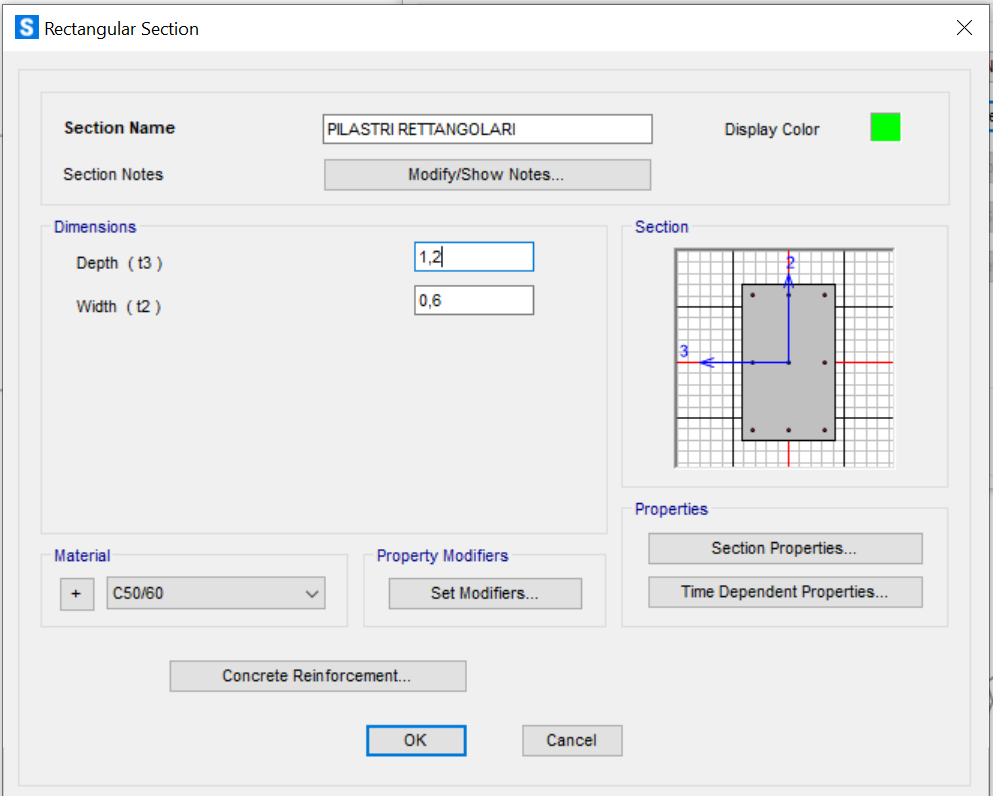
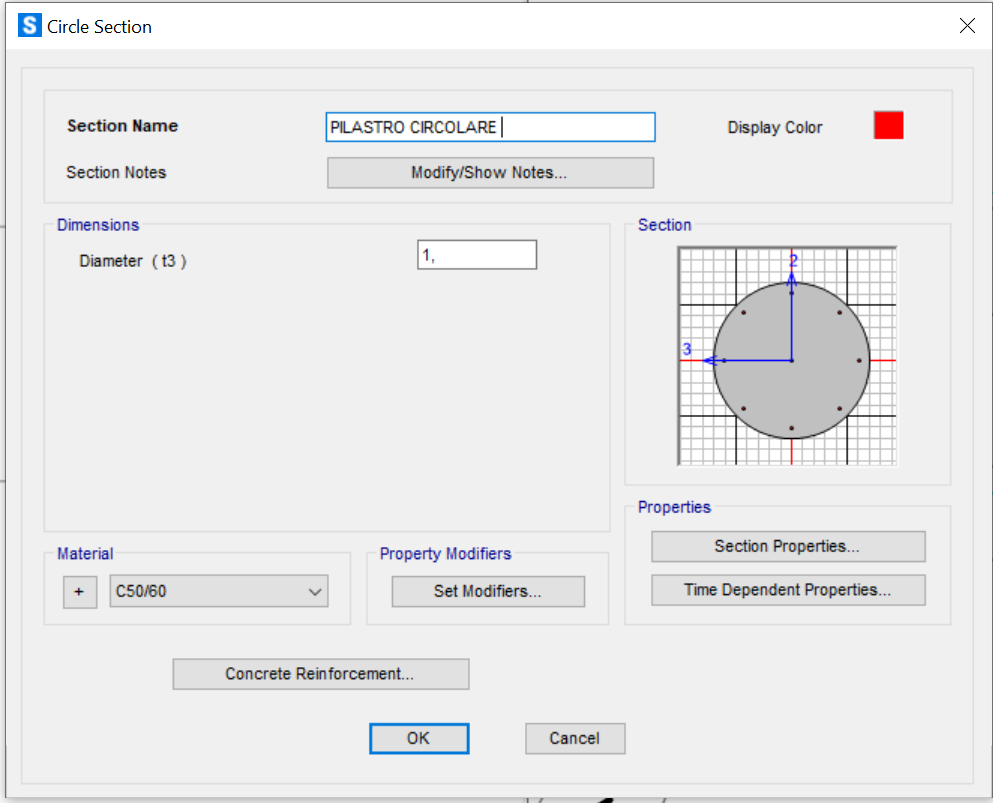
Iniziamo con il disegno su Autocad della piastra di dimensioni 38x12. Questa sarà costituita in cls C50/60. I pilastri rettangolari al di sotto della piastra avranno una dimensione di 1,2x0,6, mentre il pilastro circolare in prossimità dell’angolo un diametro di 0,8.

Pianta:

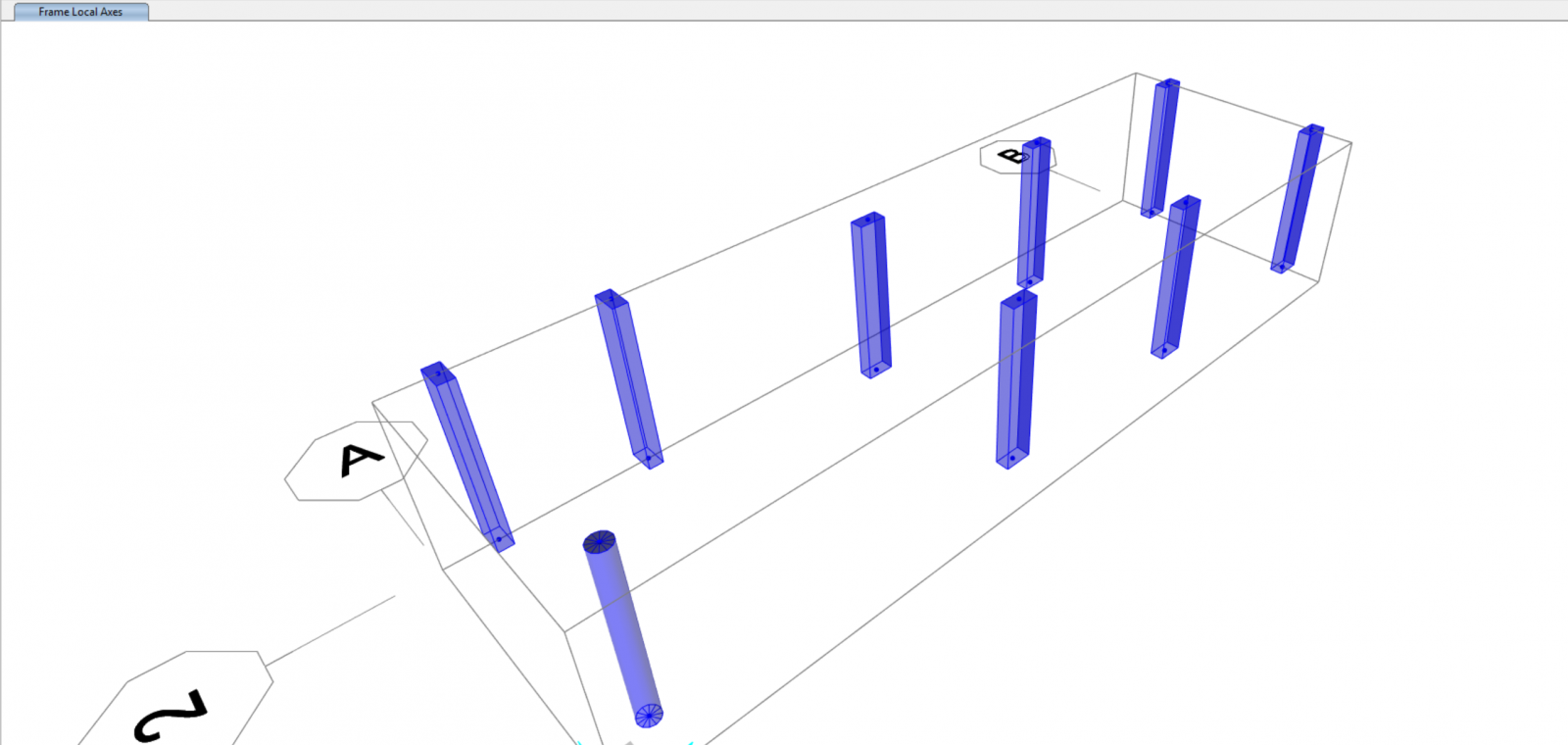
Ora passiamo su SAP2000 e ridisegniamo la nostra struttura.

Qui cambiamo immediatamente l’asse locale di alcuni pilastri perché si ottenga l’inerzia maggiore verso la direzione dello sviluppo del graticcio. (Assign-Frame-Load Axes à ruotiamo di 90°)

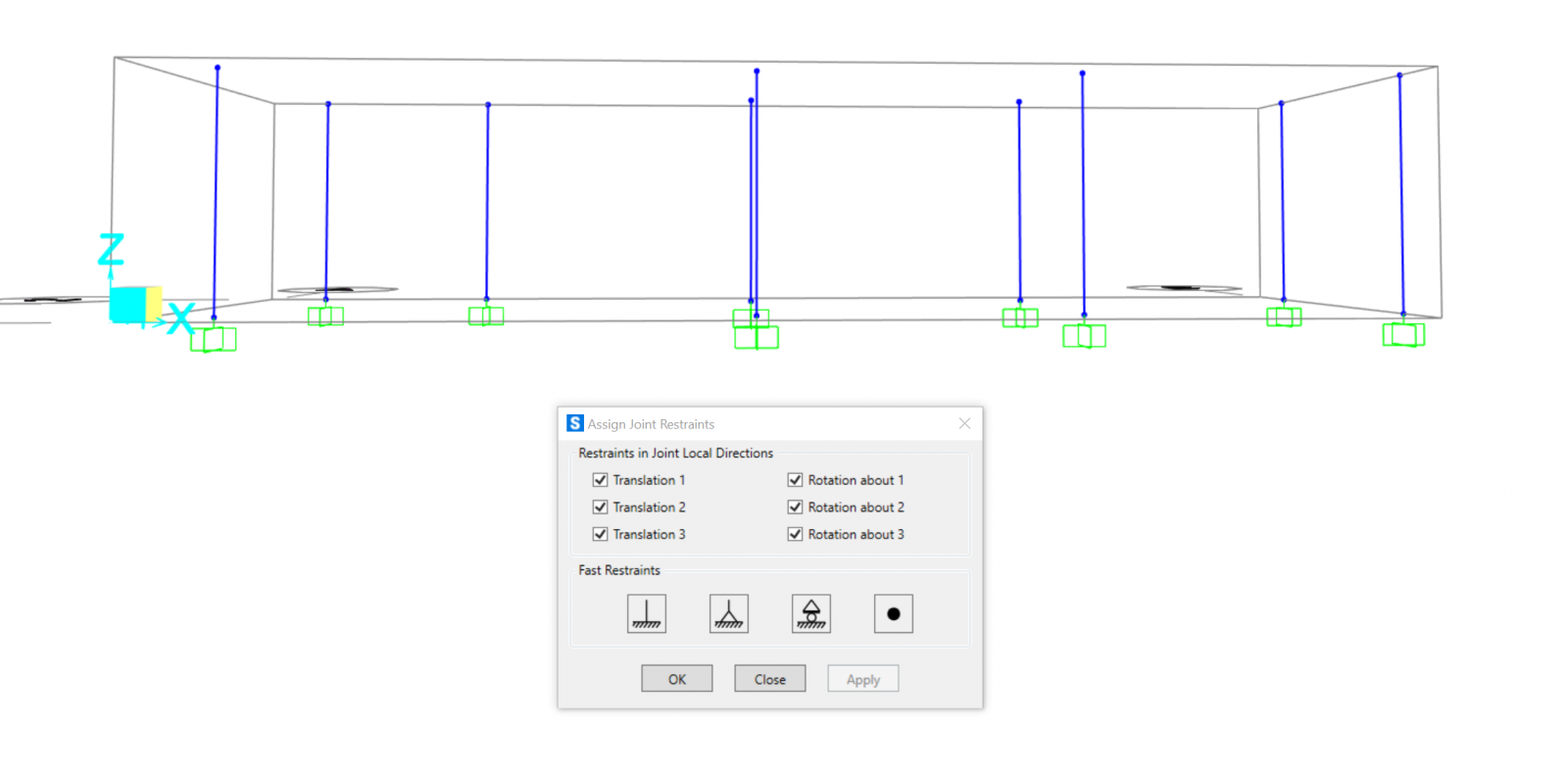
Procediamo con l’assegnazione di un vincolo esterno, in questo caso l’incastro.

Dato che la piastra è un elemento pieno, il suo coefficiente di Poisson è diverso da 0. Si utilizza quindi una piastra per avere una simulazione del graticcio. Con quest’ultimo infatti si hanno dei vuoti dove la deformazione non dà effetti secondari.

Il coefficiente di Poisson ci dice che lo sforzo normale sulla faccia di un materiale produce deformazioni primarie nella direzione dello sforzo normale, una deformazione secondaria invece nella direzione perpendicolare, di segno opposto (deformazione laterale).

Definiamo quindi il materiale per la piastra cambiando il coefficiente di Poisson, ponendolo uguale a 0, per simulare il comportamento di un sistema discreto. In questo modo si annullano gli effetti delle deformazioni nelle altre direzioni del materiale.

A questo punto definiamo la sezione della piastra (Shell section data).

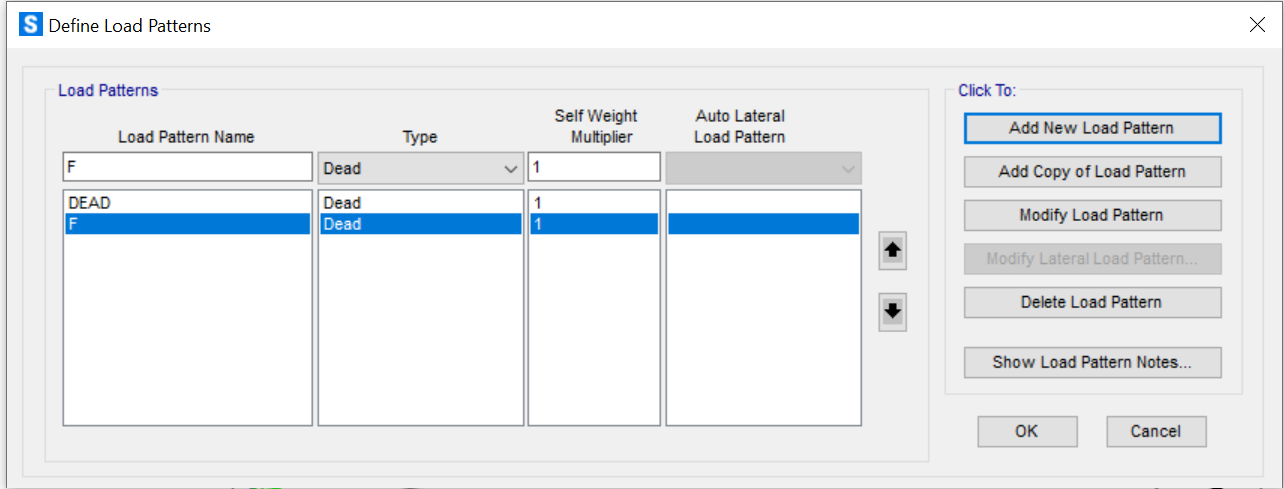
Ora definiamo il Load Pattern per assegnare dei carichi puntuali sui nodi, ponendo il moltiplicatore di Peso Proprio (Self Weight Multiplier) uguale a 1.

Procediamo nel disegno della struttura costruendo l’area (Draw Poly Area).

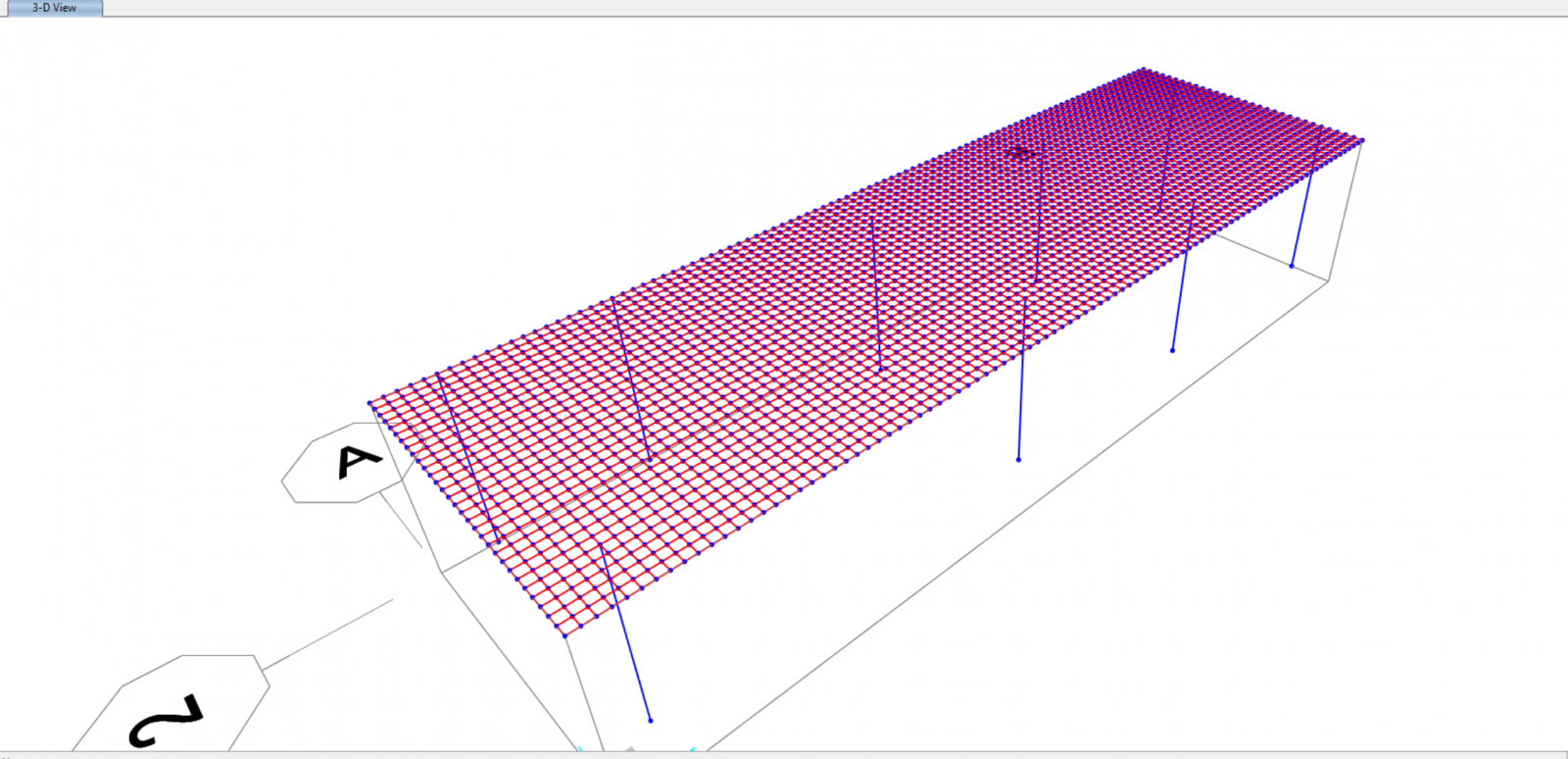
Discretizziamo successivamente l’area appena creata in moduli 0,4x04. (Divide select areas)

Suddividiamo i nodi per angolari, perimetrali e centrali.

Applichiamo i carichi:

Area 456m²

Qu = 12 kN/m²

Numero piani: 3      Q Piano 5472 kN/m²

Q Piano * 3 = 16416 kN/m²

Calcoliamo le aree d’influenza

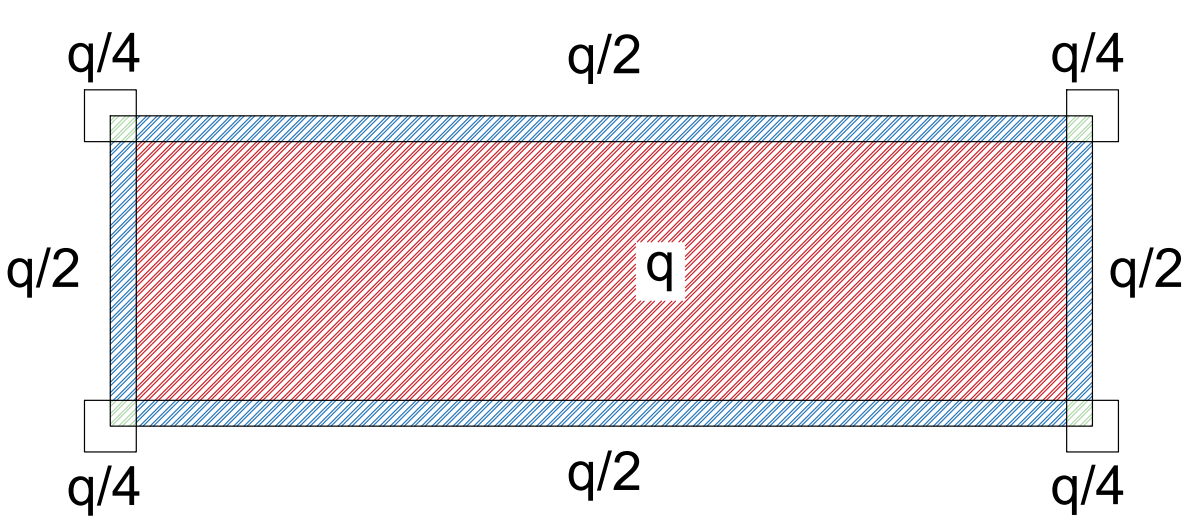
Q angolo = ¼ q

Q perimetrale = ½ q

Q centrale = 1 q

Numero nodi totale = 2976

Centrali (2726) q      Perimetrali (246) q/2     Angolari (4) q/4

Totale = 3100 Nodi

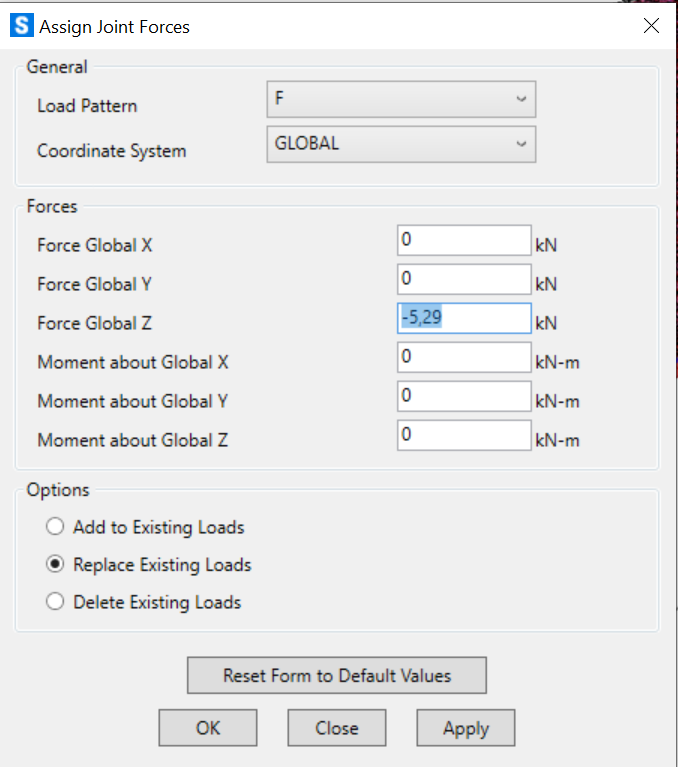
16416/3100 è 5,29 kN su ogni nodo

N centrali = 5,29 kN

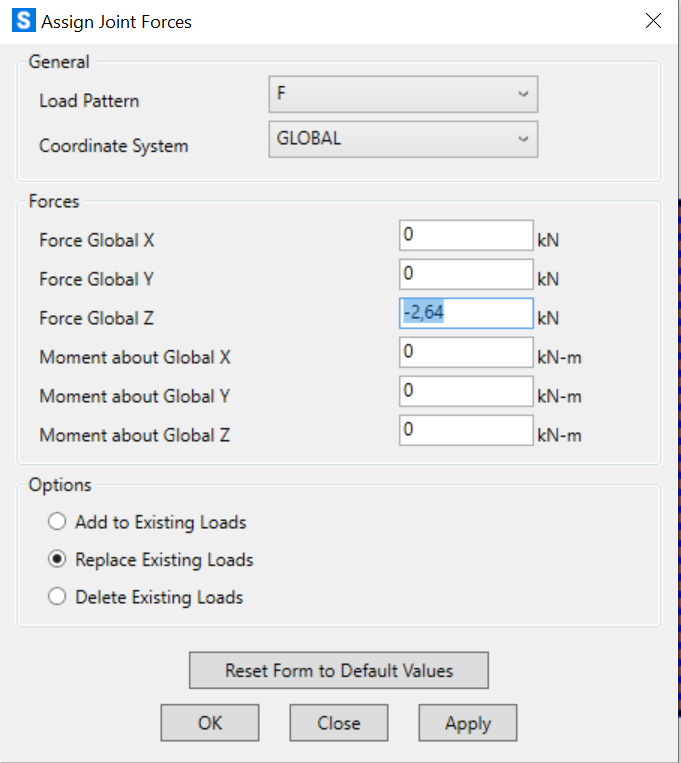
N perimetrali = 2,64 kN

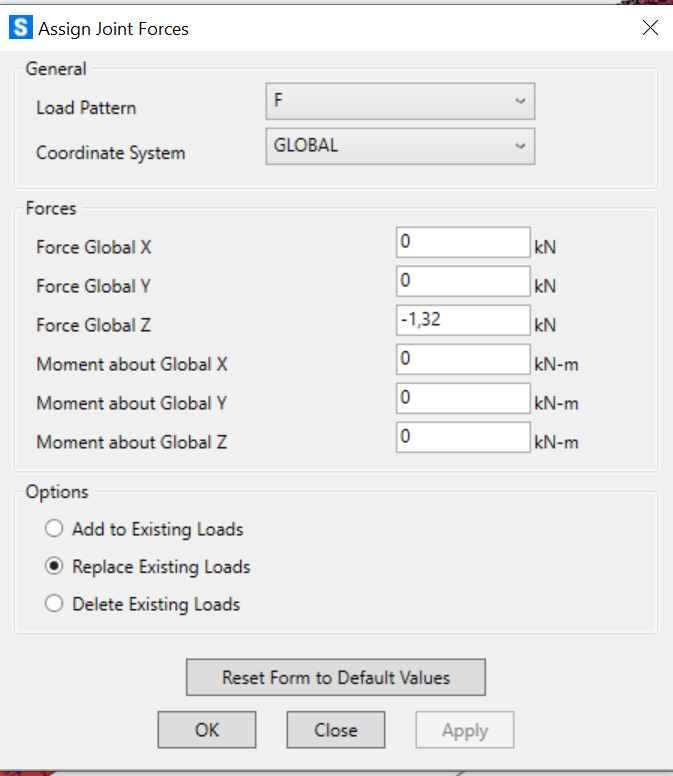
N angolari = 1,32 kN

Ora assegniamo F sui nodi

Perimetrali:

Angolari:

Centrali:

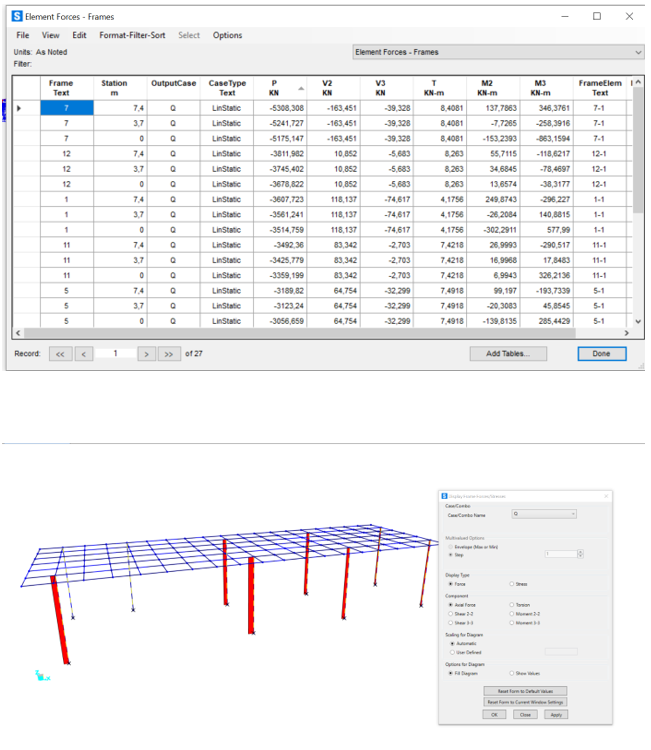
Si passa ad avviare l’analisi.

Momento M11

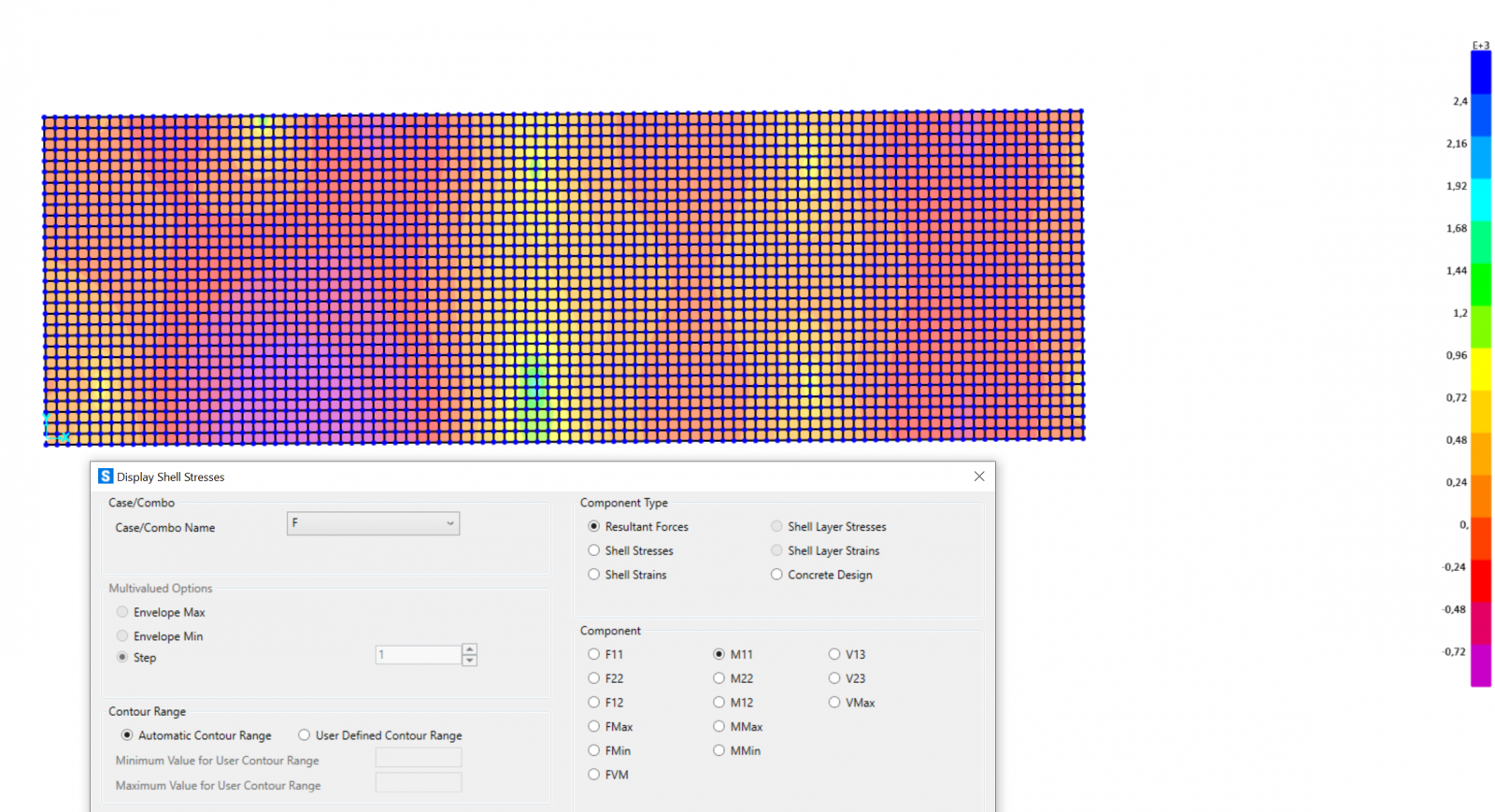
Momento M22

M Max = 2419,48 kN m

A questo punto visualizziamo le tabelle su Excel per i risultati del dimensionamento.

B=100cm   hu = 63cm  H = 68cm    VERIFICATA

Dato che i pilastri non sono posizionati lungo il perimetro della struttura, non c’è stato bisogno di allargare la trave di bordo.

Inerzia della piastra:

bh³/12 = 0,833     Ix = bh³/12

Inerzia di un passo da 2 mt

Ix = 2/12 --> 0,16m⁴

H = ³√Ix-12/b --> ³√0,16-12/0,4 --> ³√4,8 à 1,69

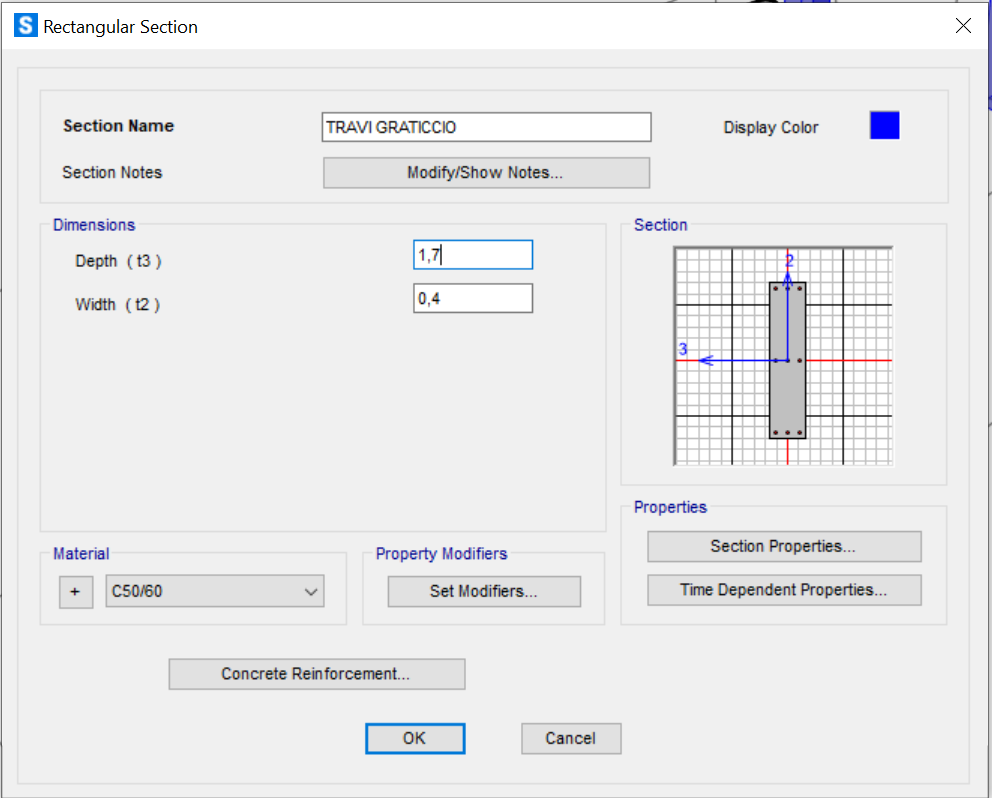
Width = b=0,4m

Depth = h = 1,70m

Ora definiamo la sezione delle travi del graticcio.

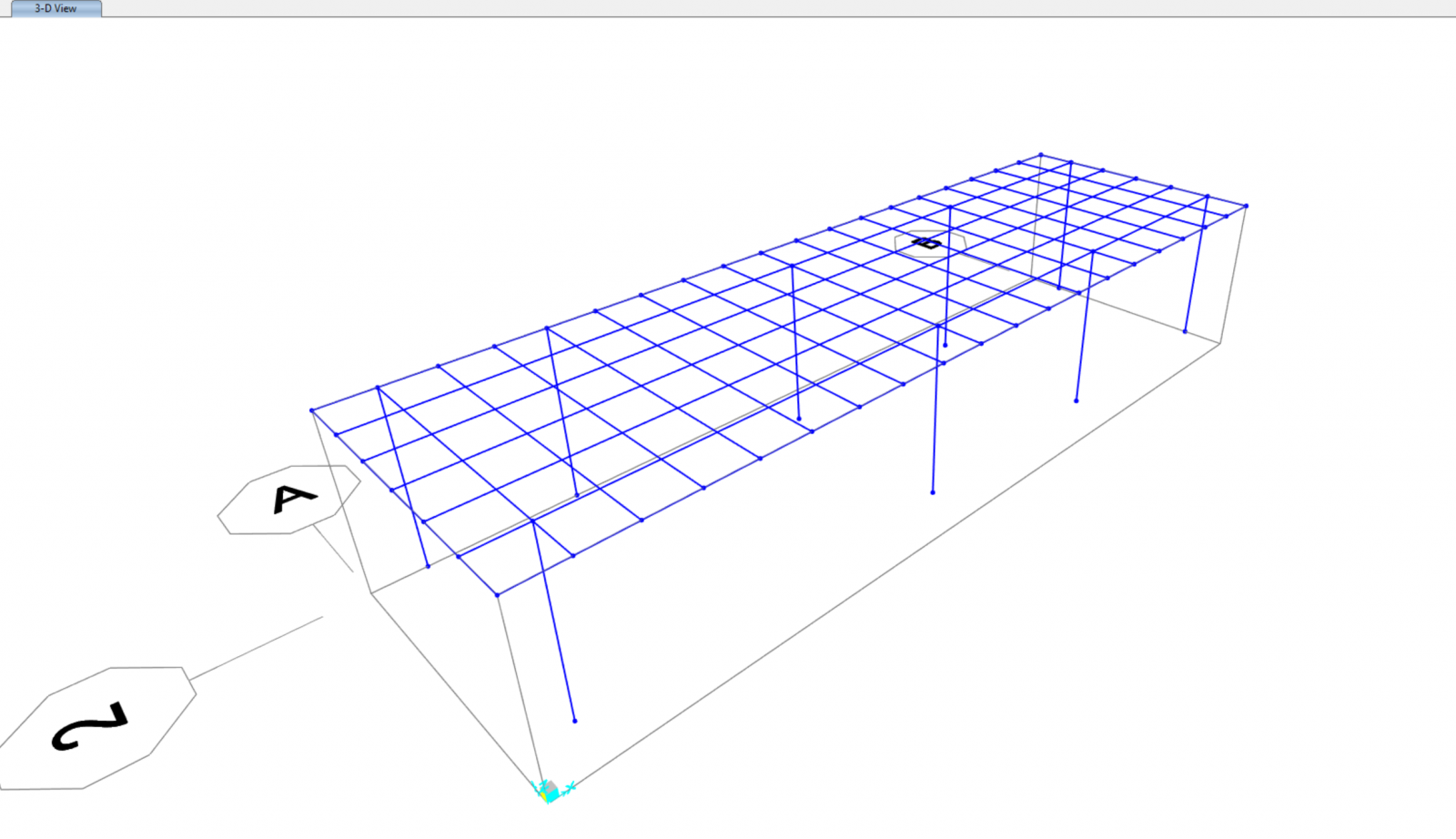
Ora dobbiamo assegnare il nodo rigido al graticcio e quindi interrompere la trave nell’intersezione.

(Divide selected frames)

Definiamo un nuovo Load Pattern Q

Q Tot = 16416 kN/m²

N nodi centrali = 90   q --> 90

N nodi perimetrali = 46   q/2 --> 23

N nodi angolari = 4   q/4 --> 1

N nodi tot = 114

16416 kn/m² / 114  --> carico concentrato sui nodi = 144 kN

144 kN  --> nodi centrali

72 kN --> nodi perimetrali

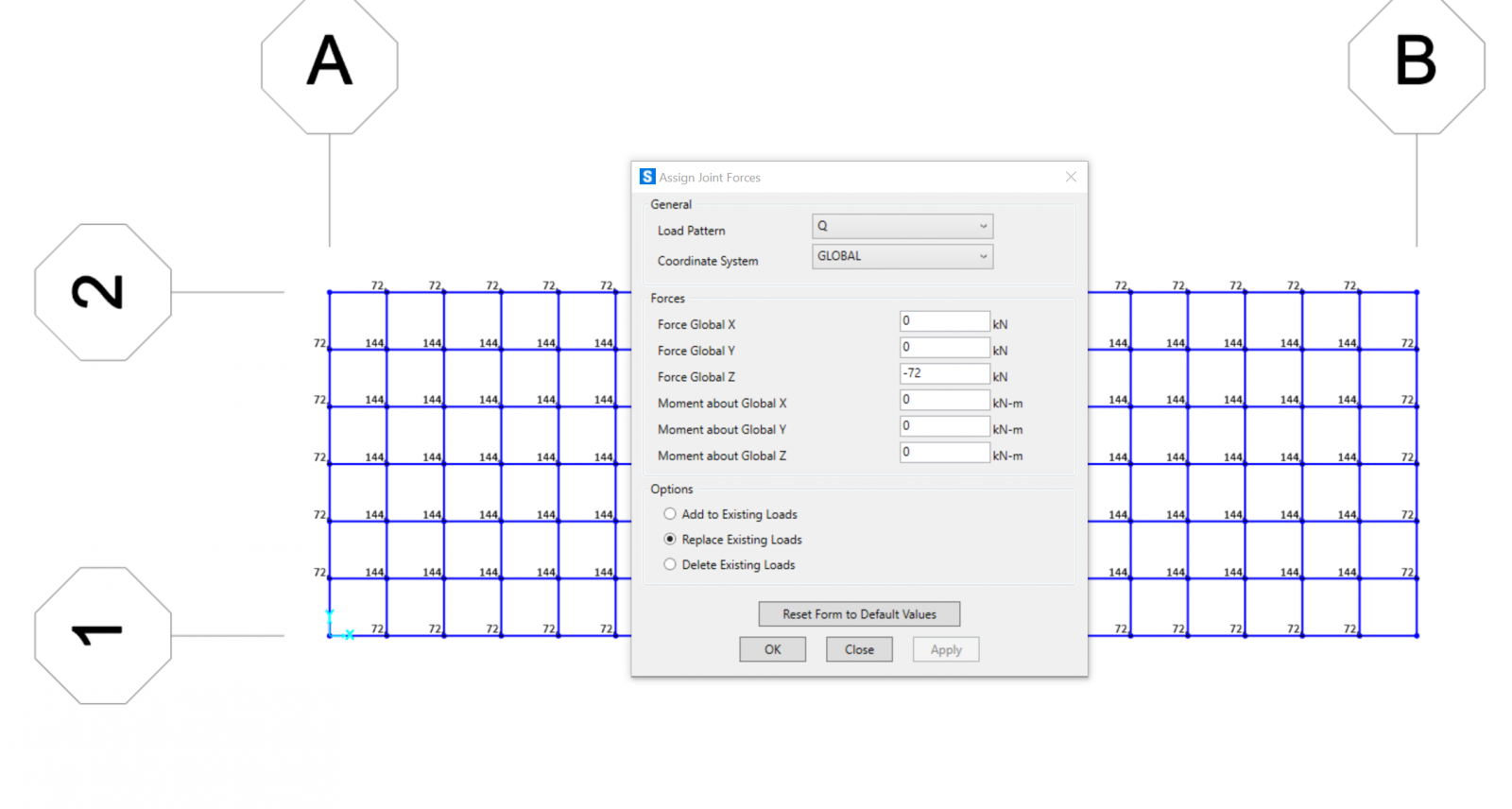
36 kN --> nodi angolari

Visualizziamo tutte le forze

Avviamo nuovamente l’analisi e visualizziamo la verifica ad abbassamento:

Δz = 0,0099m --> 9,9mm                Verificato   0,009 < 1/200l 

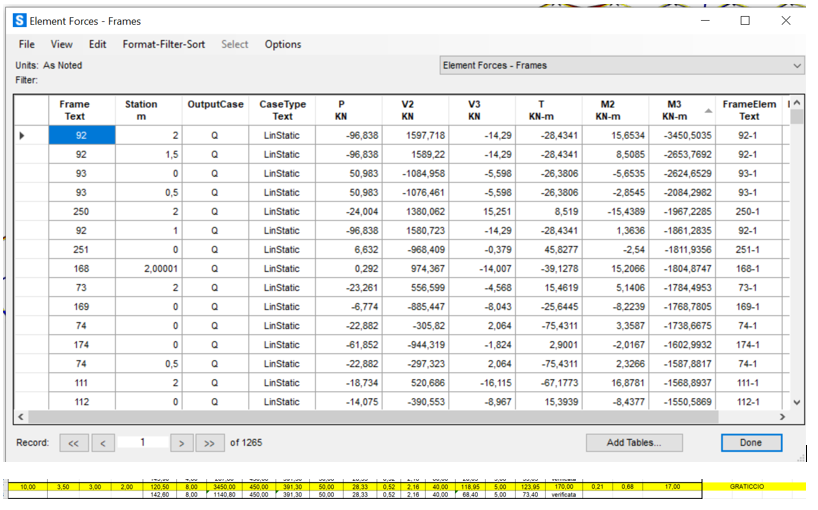
M33 Max graticcio 3450 kN/m sulle travi (FRAME 92) verificata

M33 Max pilastri 1074 kN/m (FRAME 8) verificata

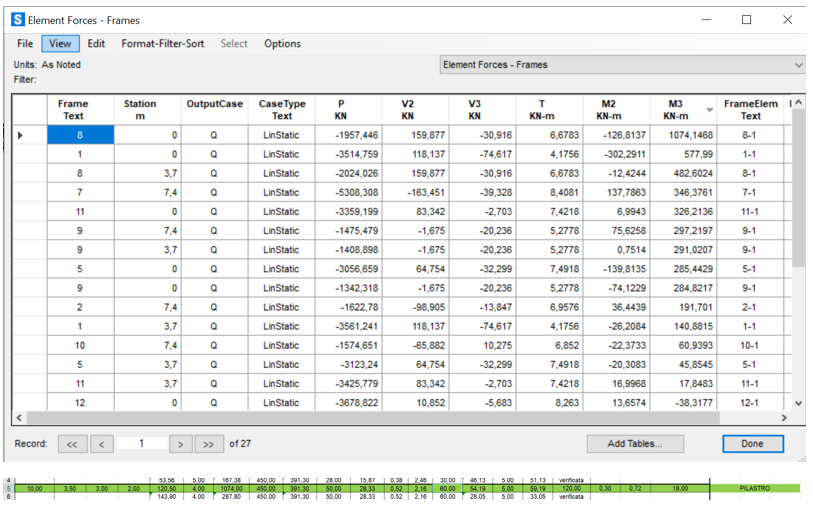
Sforzo normale sui pilastri:

Momento torcente sulla trave di bordo

Mτ = 96,54 kN/m --> 96,54*10⁶ N*mm

Τ = ἀ*Mτ/b*a²

ἀ = 3+1,8*(0,4/2) = 3,36

ἀ = 400m   ß = 200m

τ = 3,36*96,54*10⁶ / 2000*400² = 1,01 N/mm² = 1,01 Mpa < 8 Mpa   VERIFICATA A TORSIONE

 

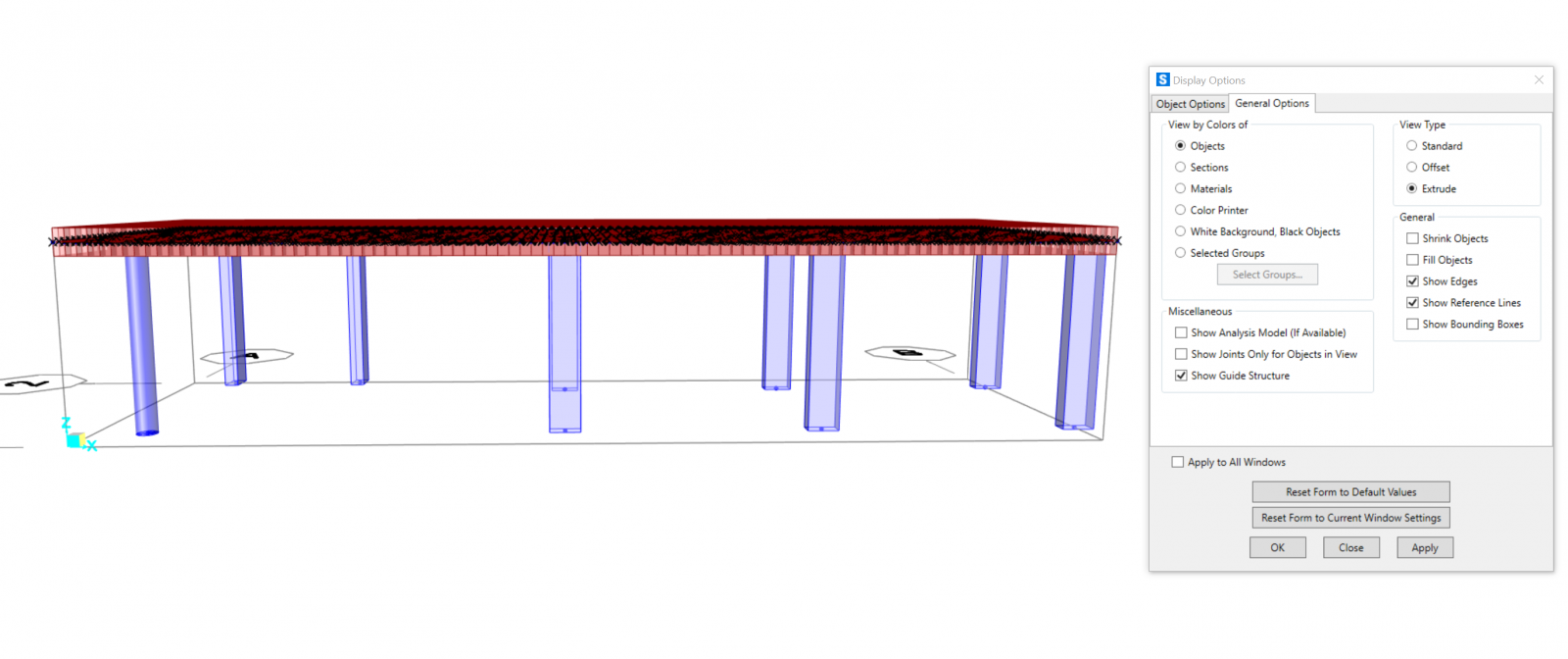
Render

 

Per l'esercitazione del progetto di un graticcio di travi inflesse è stata ipotizzata una struttura di 40 m x 20 m in pianta, sostenuta da pilastri con un interasse di 10 m. Per prima cosa è stato modellato un modello di piastra equivalente dal quale si ricava il momento di inerzia necessario a dimesionare le travi del graticcio. Quinii, si disegna la struttura su Sap2000 definendo la sezione dei pilastri, con una classe di calcestruzzo ad alte prestazioni C50/60, di dimensioni 1 m x 1 m per gli angolari, e di 1,2 m x 0,6 m per quelli intermedi, direzionandi l’orientamento dei pilastri in modo da ottenere l’inerzia maggiore lungo la direzione di dove saranno le travi del graticcio. Assegniamo il vincolo d’incastro ai pilastri, per iniziare il dimensionamento del graticcio dobbiamo per prima cosa studiare il comportamento di una piastra (Shell) in calcestruzzo.

Discretiziamo la superficie in elementi più piccoli di 0.50 m x 0.50m e assegniamo i carichi. È stato assegnato un carico distribuito indicativo di progetto pari a Qu= 10KN/m, ripartendo il carico come carico puntuale F nei nodi centrali, F/2 in quelli di bordo e F/4 negli angoli. Dall’analisi si osserva l’abbassamento max, che è accettabile perché di 2 cm, nettamente minore di 1/200 della luce massima e un Mmax di 3450 KNm.

Si utilizza il foglio excel per dedurre l’altezza della piastra trovando la sezione di una trave con un momento di inerzia equivalente a quello di una porzione di piastra larga come l'interasse delle travi del graticcio. 

Si passa al dimensionamento del graticcio.
Prendendo in considerazione l’inerzia di una fascia di 1mq della piastra e decidendo, una base di 40 cm ed un passo di 2m per le travi. Calcoliamo l’altezza del graticcio con la formula inversa;
Ix= b x h^3 / 12 
H= ( (Ix x 12)/b ) ^1/3 = 1,7 m 
Possiamo tornare su Sap2000 e disegnare il graticcio, spezzando i frame per creare dei nodi rigidi e creando un nuovo load pattern per i nuovi carichi da assegnare ad ogni nodo. Avviamo una nuova analisi e verifichiamo l’abbassamento e le sollecitazioni delle travi centrali e dei pilastri. Al fine di aumentare la rigidezza torsionale della trave di bordo, questa è stata allargata fino ad arrivare a una sezione di 1 m x 1,7 m. È stato necessario anche allungare i pilastri che sono assimilabili a dei piccoli setti.

Verifica a flessione travi

Verifica a flessione pilastri

 

 

 

 

 

 

L’esercitazione, di cui allego lo svolgimento nel file PDF, si pone l’obbietivo di mostrare come sia possibile risolvere strutture discrete complesse, come un graticcio di travi, attraverso un modello continuo equivalente più semplice.