Portale di Meccanica

 

Prima di procedere con l’esercitazione è bene definire il concetto di rigidezza. Essa può essere espressa come la forza necessaria ad imprimere uno spostamento unitario, dal momento che la forza F è pari alla rigidezza K per lo spostamento d. In sostanza è ciò che lega la causa (forza) all’effetto prodotto (spostamento): maggiore è la rigidezza, maggiore dovrà essere la forza necessaria a produrre un medesimo spostamento.

TELAIO SHEAR TYPE

Questo tipo di telaio costituisce una delle 2 configurazioni limite attraverso la quale studiamo in maniera ideale il comportamento di un portale. In particolare esso è legato intrinsecamente al concetto di rigidezza, in quanto un assunto imprescindibile è che la trave sia considerata come un corpo rigido piano, la cui rigidezza flessionale infinita non ne consente alcuna deformazione.

Non essendoci deformazione, né rotazione negli incastri tra pilastri e trave, quest’ultima trasla orizzontalmente di una lunghezza dche intendiamo conoscere. Siccome la forza F è nota, necessitiamo della rigidezza dei pilastri, unici elementi deformabili del sistema e oggetto della nostra analisi. 

Il pilastro in esame è una struttura 3 volte iperstatica dal momento che è incastrato ad entrambi gli estremi, ma possiamo imporre un cedimento vincolare elastico nell’estremo destro per il quale l’elemento si deforma. La deformazione presuppone una curvatura e di conseguenza un momento, a prescindere dalla presenza di un carico.

 

Proprio l’assenza del carico ci consente di utilizzare con maggiore semplicità l’integrazione della linea elastica:

Per trovare le 4 costanti di integrazione incognite investighiamo le condizioni al bordo:

A questo punto possiamo scrivere le equazioni dello spostamento e della rotazione:

Deriviamo la rotazione jper ottenere la curvatura. Da quest’ultima ricaviamo il Momento flettente M e il Taglio T che ne è la derivata:

Ottenute le equazioni di taglio e momento, possiamo diagrammare i due sforzi:

Le tensioni calcolate sono le reazioni vincolari nel pilastro, ma dobbiamo tenere a mente che esso fa parte di un telaio, quindi tali tensioni si trasmettono, uguali ed opposte, all’interno della trave:

PILASTRO                                                                                       TRAVE

Attraverso l’equilibrio alla traslazione orizzontale del corpo ridido trave calcoliamo il valore dello spostamento de della rigidezza:

 

In questo blog si continua a trattare il problema iperstatico, stavolta risolto col metodo delle rigidezze. In particolare viene calcolata una trave vierendeel in cui i pilastri sono infinitamente rigidi e i traversi deformabili.

SCHEMA DI CALCOLO

Per effetto delle forze esterne, i pilastri traslano, senza deformarsi, di una quantità δ.

DEFORMATA

La trave in esame ha lo stesso comportamento di un telaio “shear-type” in cui conoscendo il valore degli spostamenti  δ è possibile determinare il valore delle caratteristiche di sollecitazione e delle rigidezze dei traversi. Riferendoci, infatti, ad una trave doppiamente incastrata soggetta ad un cedimento vincolare si hanno i seguenti valori notevoli del momento e del taglio nei vincoli.

SCHEMA NOTEVOLE

Il problema iperstatico verrà, quindi, risolto scrivendo per ogni incognita (spostamento) un’equazione alla traslazione verticale.

RISOLUZIONE: 6 equazioni alla traslazione verticale per 6 incognite (δ6, δ5,δ4,δ3,δ2,δ1)

1.      F = 2T  →  F = 24 EI/l³ δ6  →  δ6= Fl³/24 EI

T = 12 EI/l³ δ6  

T = 12 EI/l³ * (Fl³/24 EI) = F/2

M = 6 EI/l²  δ6 = Fl/4

 

2.      F + F/2 + F/2= 2T  →  2F = 24 EI/l³ δ5  →  δ5= Fl³/12 EI

T = 12 EI/l³ δ5

T = 12 EI/l³ * (Fl³/12 EI) = F

M = 6 EI/l²  δ5 = Fl/2

 

3.      F + F + F= 2T  →  3F = 24 EI/l³ δ4  →  δ4= Fl³/8 EI

T = 12 EI/l³ δ4

T = 12 EI/l³ * (Fl³/8 EI) = 3/2F

M = 6 EI/l²  δ4= 3/4 Fl

 

4.      F + 3/2F + 3/2F= 2T  →  4F = 24 EI/l³ δ3  →  δ3= Fl³/6 EI

T = 12 EI/l³ δ3

T = 12 EI/l³ * (Fl³/6 EI) = 2F

M = 6 EI/l²  δ3=  Fl

 

5.      F + 2F + 2F= 2T  →  5F = 24 EI/l³ δ2  →  δ2= 5 Fl³/ 24EI

T = 12 EI/l³ δ2

T = 12 EI/l³ * (5 Fl³/24 EI) = 5/2F

M = 6 EI/l²  δ2=  5/4Fl

 

6.      F + 5/2F + 5/2F= 2T  →  6F = 24 EI/l³ δ1  →  δ1= Fl³/4 EI

T = 12 EI/l³ δ1

T = 12 EI/l³ * (Fl³/4 EI) = 3F

M = 6 EI/l²  δ1=  3/2 Fl

Determinato Taglio, Momento e rigidezze dei traversi, trovo momento e taglio anche nei pilastri.

DIAGRAMMA TAGLIO E MOMENTO

Allo stesso modo di prima, siamo in grado di risolvere lo stesso tipo di trave, stavolta doppiamente incastrata.

SCHEMA DI CALCOLO

Bisogna notare che la trave è simmetrica e simmetricamente caricata per cui basta studiarne la metà ed in corrispondenza della simmetria bisogna considerare la forza di valore pari a F/2

DEFORMATA

RISOLUZIONE:3 equazione alla traslazione verticale per 3incognite (δ3,δ2,δ1)

1.      F/2 = 2T  →  F = 48 EI/l³ δ3  →  δ3= Fl³/48 EI

T = 12 EI/l³ δ3  

T = 12 EI/l³ * (Fl³/48 EI) = F/4

M = 6 EI/l²  δ3= Fl/8

 

2.      F + F/4 + F/4 = 2T  → 3/2 F = 24 EI/l³ δ2  →  δ2= Fl³/16 EI

T = 12 EI/l³ δ2  

T = 12 EI/l³ * (Fl³/16 EI) = 3/4 F

M = 6 EI/l²  δ2= 3/8 Fl

3.      F + 3/4F + 3/4F = 2T  → 5/2 F = 24 EI/l³ δ1  →  δ1= 5 Fl³/48 EI

T = 12 EI/l³ δ1  

T = 12 EI/l³ * (5 Fl³/48EI) = 5/4 F

M = 6 EI/l²  δ1= 5/8 Fl

TRAVERSI

PILASTRI

DIAGRAMMI TAGLIO E MOMENTO

VERIFICA IN SAP2000

Questione cruciale consiste nel far capire al programma che i pilastri sono infinitamenti rigidi. Per fare ciò, o si dà un valore elevato al modulo di Young al materiale con cui è fatto il pilastro, o si aumenta a dismisura la sezione del pilastro stesso. In particolore ho dato un valore altissimo al modulo di Young del materiale che costituisce il pilastro a cui tra l'altro ho assegnato una sezione di 1m x 1m, mentre alla trave è stata assegnata una sezione molto piccola.

Di seguito vengono proposti gli schemi finali:

Esercizio 1

DEFORMATA

DIAGRAMMA MOMENTO

DIAGRAMMA TAGLIO

Esercizio 2

DEFORMATA

DIAGRAMMA MOMENTO

DIAGRAMMA TAGLIO

Trave Vierendeel

• La trave è infinitamente resistente a flessione (momento di inerzia molto alto)
• I pilastri non si deformano se sottoposti ad un qualsiasi sforzo normale

Telaio Shear Type

Il Telaio Shear Type costituisce una delle 2 configurazioni limite attraverso cui si studia il comportamento di un portale. Questo schema ideale si basa sul concetto di rigidezza, infatti nelle condizioni iniziali si pone che la trave sia un corpo rigido, la cui rigidezza flessionale infinita non ne consente alcuna deformazione. In aggiunta, i pilastri su cui essa è appoggiata, vengono considerati non deformabili assialmente e collegati alla trave con nodi a incastro. Tutto questo condiziona notevolmente la trave, che non può ruotare ma solamente traslare orizzontalmente. Analizzare e risolvere questo tipo di struttura vuol dire studiare i pilastri, unici elementi deformabili (solo flessionalmente) da cui ricavare i valori di taglio e momento per poi capire in seguito come essi si trasmettono alla trave.

---

Trave Vierendeel a sbalzo

La seguente trave Vierendeel può essere risolta esattamente con lo stesso metodo utilizzato per risolvere un telaio shear type.
La trave sotto esame infatti altro non è che uno schema di telaio shear type disposto orizzontalmente, nel quale tutti i nodi sono a incastro e in cui i montanti verticali vengono considerati a rigidezza flessionale e assiale infinita e quelli orizzontali a rigidezza assiale infinita.

Per prima cosa troviamo i valori del taglio in corrispondenza di ogni forza esercitata sulla trave, per mezzo dell’equazione di equilibrio alla traslazione. È evidente che una volta capito il meccanismo attraverso cui si ripartiscono le forze lungo la trave, si possono trascrivere facilmente i valori del taglio senza fare troppi calcoli. Eseguire i calcoli però ci fornisce anche un altro dato importante, ovvero il valore δ dello spostamento del ritto e quindi della deformazione della trave; trovati i valori degli spostamenti di ogni ritto potremo disegnare la deformata.

Ora posso procedere al disegno di massima della deformata.

 

Dallo schema della deformata ottengo un’informazione precisa: dove la curvatura è nulla, cioè dove ho un flesso nella deformata, anche il momento sarà nullo, questo mi facilita la comprensione del diagramma del momento.

Con questa informazione, per trovare il valore dei momenti sulle parti della trave fra le aste verticali, basta moltiplicare il valore di ciascun taglio trovato in precedenza, per il braccio l/2.
Esempio: F/2 x l/2 = Fl/4

I diagrammi di momento e taglio sui ritti devono essere calcolati invece nel seguente modo:
per il primo, si devono equilibrare i nodi, ovvero bisogna equilibrare  i momenti trovati in precedenza sulle travi, con un momento interno alla ritto.
Esempio: Fl/2+Fl/4 = (1/4+2/4)Fl = 3/4Fl

Per il diagramma del taglio, bisogna equilibrare il momento del ritto (appena calcolato) con una coppia di forze, il cui valore è il valore del taglio in quel punto; si calcola moltiplicando per due i momenti agenti sul traverso e dividendo per il braccio della coppia “l”.
Esempio: Fl/4 x 2/l = F/2

Ora posso disegnare il diagramma del taglio e del momento:

Verifico su Sap2000 che la deformata e i diagrammi delle sollecitazioni ottenuti, siano esatti o quanto meno credibili.



Il risultato è molto simile in tutti e tre i casi. Da notare una leggera rotazione delle aste verticali nello schema della deformata.

---

Trave Vierendeel incastrata ai bordi

In questo secondo caso di studio, ho una trave Vierendeel vincolata a entrambi gli estremi; procedo nella stessa maniera del primo caso di studio, sfruttando però la palese simmetria di questo schema strutturale e tenendo conto che la forza agente sul ritto centrale si ripartisce su 4 traversi.

Procedo ai calcoli per trovare i valori dello spostamento di ogni asta e i valori del taglio sui traversi, partendo dall’asta centrale:

Disegno la deformata.

Calcolo anche i valori del momento sui traversi, moltiplicando i valori del taglio, ottenuti in precedenza, per il braccio “l/2”.

Passo ora al calcolo del diagramma del momento e del taglio sulle aste.

Equilibrio dei nodi:

Equilibrio delle aste:

Posso ora disegnare i diagrammi delle sollecitazioni su travi e aste:

Verifico i risultati ottenuti su Sap2000.

 

I risultati anche in questo caso sono molto simili!

 

RISOLUZIONE DI UN SISTEMA IPERSTATICO MEDIANTE IL METODO DELLE FORZE

 

 

Per la risoluzione dello schema statico qui rappresentato verrà applicato il metodo delle forze, che prevede di declassare vincoli fino a raggiungere l'isostaticità e sostituendoli con forze incognite, che corrispondono alle reazione che i vincoli appena esclusi fornirebbero come risposta ai carichi agenti.

La scelta dei vincoli da declassare è dettata dalla conoscenza del valore di abbassamenti e rotazioni nelle condizioni di carico e schema strutturale che si presenta. In questo caso trasformare le cerniere esterne in cerniere interne aggiungendo dei momenti agenti a destra e a sinistra risolve il problema agevolmente: i momenti infatti ripristinano la condizione di vincolo esclusa, garantendo la simmetria delle rotazioni a destra e a sinistra della cerniera interna appena inserita. Inoltre è noto il valore della rotazione in quell'ambito. Al contrario, declassando la reazione verticale dei carrelli e sostituendola con delle forze verticali, per risolvere il problema sarebbe stato necessario conoscere gli abbassamenti della trave non solo in mezzeria, ma anche a ¼L (valore valido anche a ¾ della lunghezza per simmetria di condizioni di carico e vincolo). Per arrivare a queste informazioni sarebbe stato necessario applicare il metodo della linea elastica, grazie al quale sono note le informazioni riguardo i valori delle rotazioni e abbassamenti nelle condizioni che si presentano in questo caso. Nel caso del momento applicato all'estremo è importante considerare che non imprime solo una rotazione nel punto in cui è applicato, ma anche una rotazione di entità dimezzata all'altro estremo.

 

 

Questo è lo schema alternativo, risultato dell'applicazione del metodo delle forze.

 

 

I momenti aggiunti in seguito al declassamento dei vincoli sono ovviamente incogniti. Per trovarne il valore bisogna eguagliare le rotazioni a destra e a sinistra della cerniera, eguaglianza che questi stessi momenti assicurano. Sempre grazie alla simmetria delle condizioni di carico e di vincolo è possibile considerare X₁ = X₃.

Per trovare il valore di X₁ ed X₂ è sufficiente mettere a sistema 2 equazioni ottenute eguagliando le rotazioni a destra e a sinistra dei punti B e C.

 

 

trovato il valore dei momenti è possibile calcolare le reazioni vincolari dei 2 sistemi, quello con i momenti e quello con il carico ripartito, considerando la trave sempre come discontinua.

La somma delle reazioni, per il principio di sovrapposizione degli effetti, darà come risultato quelle della struttura obbiettivo dell'esercizio.

 

 

 

Ora è possibile disegnare i grafici del Taglio e del Momento flettente lungo la trave.

Anche se un poco in ritardo, eccomi qui. 

Veniamo direttamente al punto: si deve dimensionare la strutture portante di un solaio a nostra scelta, scegliendo autonomamente la tecnologia: nel mio caso, sarà il legno (è ora che anche qui in italia si inizi ad utilizzarlo consapevolmente e coscientemente!).

Prima di tutto, ho stabilito le dimensioni del solaio di riferimento (6m x 10m), proseguendo poi nello scegliere con cura i vari "strati" del pacchetto solaio, al fine di ottenere una situazione "comune" di carichi, ma anche tecnologicamente efficiente (qui sotto potete vedere la composizione del pacchetto più una piccola keyplan del solaio). 

Il solaio è così composto:

1) Listelli per controsoffitto in legno di FAGGIO, 2cm x 5cm, intervallati tra essi di 2cm (PESO SPECIFICO di 7,5 KN/mc)

2) Struttura metallica per sostegno controsoffitto (PESO SPECIFICO IRRILEVANTE)

3) Travetti in legno lamellare combinato GL24c da dimensionare (PESO SPECIFICO di 3,5 KN/mc)

4) Tavolato di spessore 1,5cm di legno di castagno (PESO SPECIFICO di 4,85 KN/mc)

5) Isolante in fibra di legno 10cm (PESO SPECIFICO di 1,8 KN/mc)

6) Tavolato irrigidente di spessore 1,5cm di legno di abete (PESO SPECIFICO di 3,5 KN/mc)

7) Strato di sottopavimento per i rumori da calpestio (PESO SPECIFICO IRRILEVANTE)

8) Parquet scuro di spessore 1cm (PESO SPECIFICO di 9,5 KN/mc)

E ora, sono cavoli. Ai fini del dimensionamento di una trave, importantissima è la luce che ricopre essa stessa, e la porzione di solaio che deve sorreggere (notare lo schemino nell'immagine precedente, in alto a sinistra.)

Come è chiaro, la trave più sollecitata è quella centrale, che su una luce di 6m, "sostiene" il peso di una porzione di solaio di interasse di 5m (gli altri 5 sono suddivisi 2,5m per ciascuna trave tra le due rimanenti, parallele).

Bene, a noi la nostra amata normativa.  Per dimensionare la trave, dobbiamo sommare le 3 combinazioni di carichi che agiranno su essa, come riportato dalla noramativa: questa suddivide i carichi in Qs (strutturali, come travetti e tavolato), Qp (portati, ossia tutto ciò di cui è composto il solaio, considerando anche il peso dei tramezzi di 1KN/mq e degli impianti di 0,5KN/mq), e Qa (accidentali). Per quest'ultima categoria, ci vengono già dati dei cairichi su mq, a seconda della destinazione d'uso dell'edificio per il quale stiamo progettando la trave; quello da me scelto, è un edificio per civile abitazione, quindi, il valore Qa, come da normativa, è di 2KN/mq).

Come avete notato se FOSSE STATI ATTENTI, il Qa è espresso in KN/mq, e non KN/mc come i materiali precendetemente elencati...e quindi?????  Quindi, con calcolatrice alla mano, moltiplichiamo ogni peso specifico per lo spessore scelto del materiale, in modo da ottenere il peso per superficie dei singoli materiali scelti!! Ora, abbiamo le nostre 3 combinazioni di carico, espresse per forza su unità di superficie, fantastico!!!! 

C'è un però: per fare i precisini, per ogni combinazione di carico, dobbiamo applicare un coefficiente di sicurezza, ossia dei "numeri" che mi vanno ad alterare in modo più sfavorevole, la mia situazione di carico, al fine di ottenere una progettazione con un più alto valore di sicurezza. Nello specifico, chiamati "gamma"  valgono 1.1 per i Qs, e 1,5 per i Qp e Qa.

A noi progettazione!!!  Chiaramente con l'aiuto di un foglio excel, (anzi, IL foglio excel scaricabile da questo sito, nella sezione downloads), avevate dubbi???)

Il foglio excel, è stato da me leggermente modificato, inserendo nelle formule come già detto, i valori "gamma" di sicurezza; ma non solo: ora il foglio è impostato non solo per il calcolo della trave, ma anche PRIMA SU TUTTO IL DIMENSIONAMENTO DEI TRAVETTI, e successivamente per la verifica della trave scelta CONSIDERANDO IL CONTRIBUTO DEL PROPRIO PESO!!!

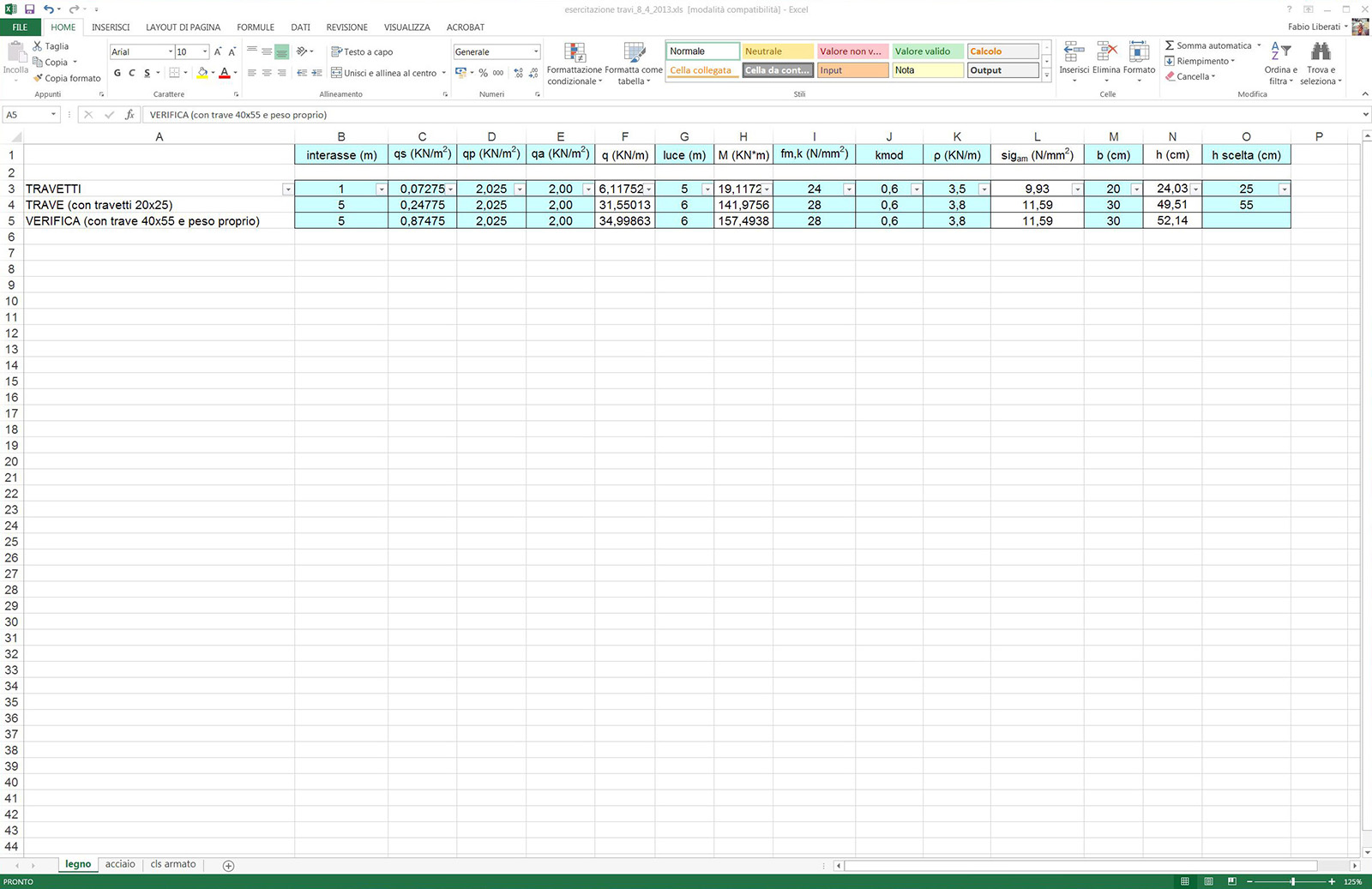
Infatti, come noterete dalla tabella che segue, prima ho considerato i Qs escludendo i travetti, in modo da poterli CORRETTAMENTE DIMENSIONARE, basandomi su materiale scelto (legno lamellare combinato GL24c).

Una volta dimensionati, li ho inclusi con il proprio peso nel Qs, al fine di dimensionare la trave.

Ma, se mi fossi fermato qui, vedete come dalla seconda riga risulta che avrei necessità di una trave alta 50cm una volta fissata la base... e invece NO!!! Sbagliato, poichè la trave, HA UN PROPRIO PESO, e non indifferente!!

Ergo, sapendo che le travi vengono prodotte generalmente con scarti di 5cm, ho scelto una trave alta 55cm, e ho verificato se questa volta, fosse stata in grada di portare il solaio e se stessa...

Et voilà!!!  TRAVE PROGETTATA E VERIFICATA!

 

 

 

 

 

 

 

Esercitazione 5

Metodo delle rigidezze – Trave Vierendeel

Una trave Vierendeel puo’ essere idealizzata come equivalente ad uno schema di telaio shear type coricato, in cui i montanti verticali vengono quindi considerati a rigidezza infinita.

 

Si osservano immediatamente i caratteri di simmetria di cui gode la struttura. Si può così procedere ad analizzarne solo una metà, aspettandoci che gli stessi risultati siano applicabili all’altra. 

 

Si procede quindi con la definizione delle reazioni vincolari, ricordando la somiglianza con la struttura shear type.

 

Si hanno ora tutte le informazioni per disegnare il grafico del taglio:

 

Sempre tenendo presente le somiglianze con il telaio shear type, ci aspettiamo che la legge del momento nei tratti orizzontali abbia un punto di nullo alla metà di ogni tratto. Sapendo inoltre  che tale legge sarà lineare, data la presenza di soli carichi puntuali, per disegnarne il grafico ci occorrono soltanto due valori certi per i quali far passare una retta. Si scelgono per comodità  quelli agli estremi, che saranno uguali in modulo e di segni opposti. Infatti si può scrivere l’equazione di equilibrio dei momenti rispetto ad l/2, dove la risultante sappiamo che sarà nulla (perché il grafico ha un nullo). 

Da cui otteniamo tali risultati:

 

Per ottenere i valori del momento per i tratti verticali, invece, imponiamo l’equilibrio dei nodi:

 

N.B. Per ragioni di simmetria, escludiamo a priori la possibilità che il montante verticale centrale sia soggetto a momento.

Andando quindi a ricomporre le due parti della struttura si ottengono  i seguenti diagrammi: