Risoluzione di una Trave reticolare con il metodo di Ritter
Per risolvere questa trave reticolare posso utilizzare il metodo di Ritter che prevede l'analisi dello sforzo normale di tre aste tagliate da una sezione
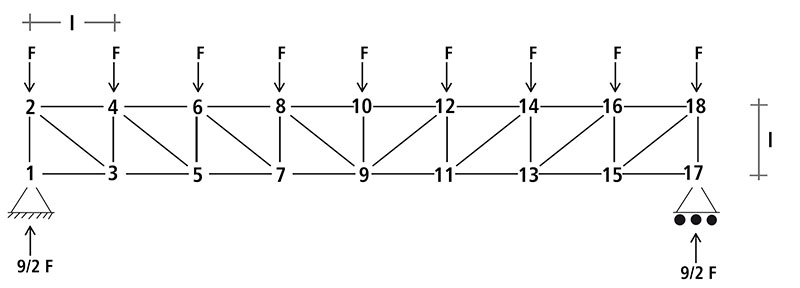
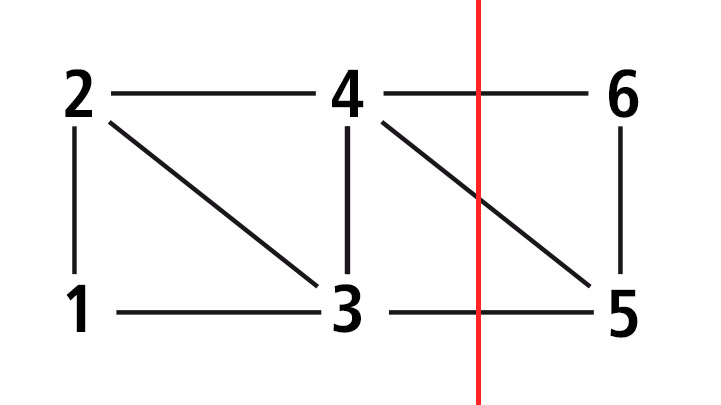
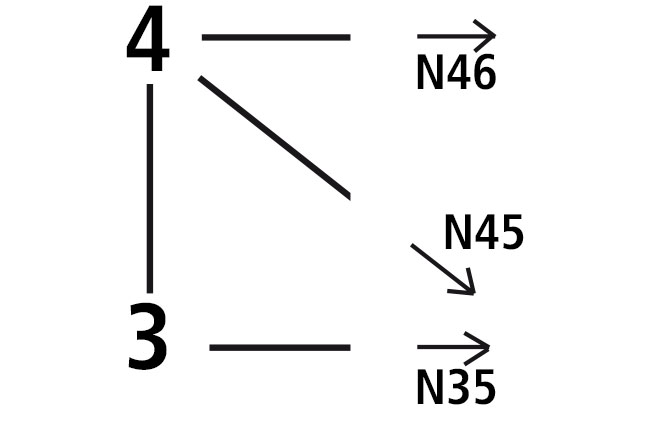
Utilizzo il punto 5 come centro di rotazione di N46: - N46*l - 9/2 F *2l + F*l + F*2l = 0 N46 = - 6 F
Utilizzo il punto 4 come centro di rotazione di N35 + N35*l - 9/2 F*l + F*l = 0 N35 = 7/2 F
L'asta obliqua è inclinata di 45° rispetto alla trave e al montante quindi dovrò utilizzare il seno o il coseno di 45 ( √2/2)
N45 * √2 /2 + 7/2 F - 6F N45 = 5 √2 /2 F
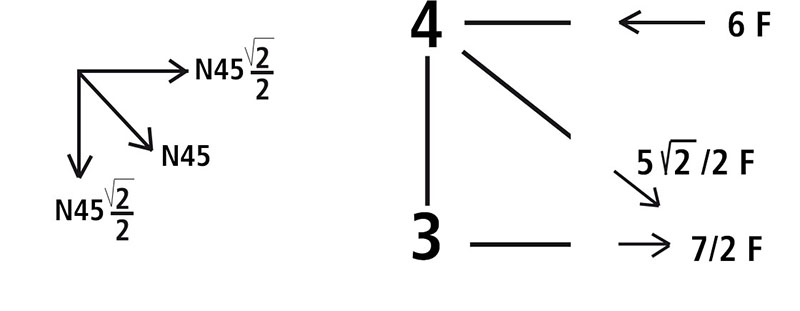
Con lo stesso metodo trovo le sezioni delle aste di metà trave (l’altra metà sarà simmetrica)
- N24*l - 9/2 F*l + F*l = 0 N24 = - 7/2 F
+ N13*l = 0 N13 = 0 (asta scarica)
+ N23√2 /2 - 7/2 F = 0 N23 = 7 √2 /2 F
- N68*l - 9/2 F*3l + F*6l = 0 N68 = - 15/2 F
+ N57*l - 9/2 F*2l + F*3l = 0 N57 = 6 F
+ N67√2 /2 - 15/2 F + 6 F = 0 N67 = 3 √2 /2 F
- N810*l - 9/2 F*4l + F*10l = 0 N810 = - 8 F
+ N79*l - 9/2 F*3l + F*6l = 0 N79 = 15/2 F
+ N89 √2 /2 + 15/2 F - 8 F = 0 N89 = √ 2 /2 F
Per i montanti verticali eseguo sempre una sezione di Ritter su tre aste per ricavarne la normale
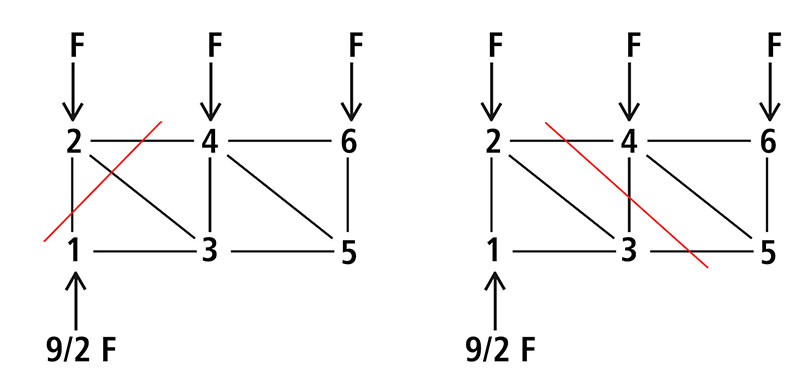
+ N12 + F + 7 2 /2 * 2 /2 F = 0 N12 = - 9/2 F
+ N34 - F + 9/2 F = 0 N34 = - 7/2 F
+ N56 - 2F + 9/2 F = 0 N56 = - 5/2 F
+ N78 - 3 F + 9/2 F = 0 N78 = - 3/2 F
+ N910 + F = 0 N910 = - F
A questo punto ho tutti gli sforzi normali di metà trave che si ripeteranno simmetricamente sulla seconda metà consentendomi di disegnare il diagramma dello sforzo normale di tutta la trave reticolare
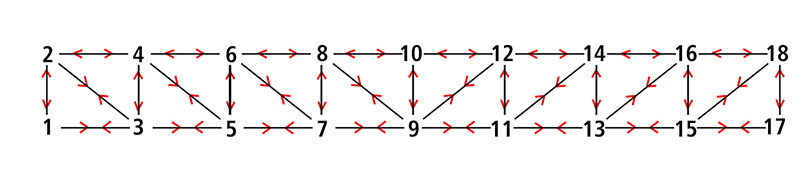
Ho assegnato alla lunghezza delle aste l = 1m e alla forza applicata sui nodi F = 100 N

Risoluzione della struttura in SAP 2000
Stabilisco l’unità di misura (KN,m,C), disegno la trave ed associo il peso proprio della struttura pari a 0 (Define -> Load Patterns)
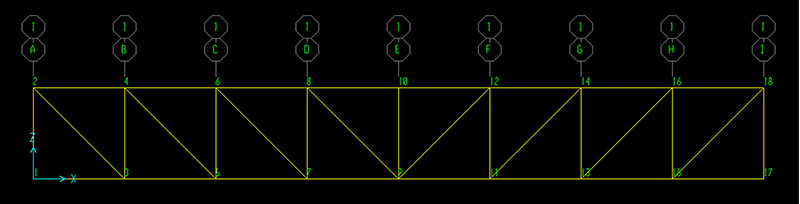
Ora inserisco i due vincoli ai vertici della struttura (Assign -> Joint -> Restraints) ed inserirsco le cerniere interne alle aste assegnando un rilascio (Assign -> Frame -> Releases/Partial Fixity)
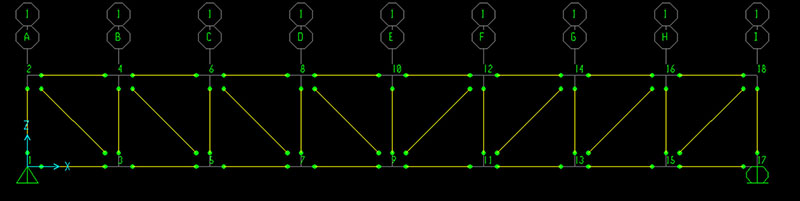
Devo assegnare un profilo alle varie aste quindi scelgo un tubolare in acciaio (Define -> Section Properties -> Frame Sections) definendone il diametro e lo spessore. Dopo aver definito il profilo posso associarlo alle aste della struttura reticolare (Assign -> Frame -> Frame Sections)
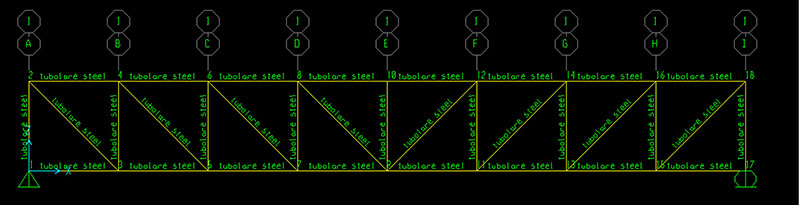
A questo punto vado ad inserire le mie forze di F = 100 N applicate sui nodi nella parte alta della trave (Assing -> Joint Loads -> Forces). Le forze dovranno riportare segno negativo poichè orientate verso in basso con verso opposto alla Z del sistema di riferimento
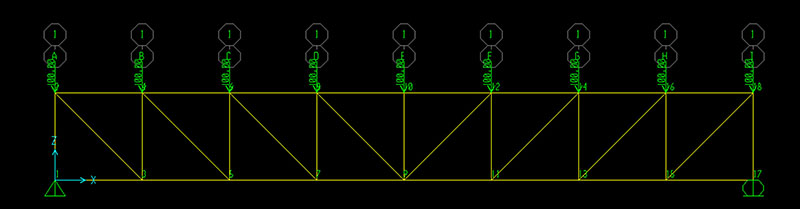
La mia struttura a questo punto ha sia vincoli che forze applicate e può essere calcolata (Run Analysis). Visto che è una struttura reticolare avrà solo sforzi normali che posso visualizzare nel diagramma della normale (Show Forces/Stresses ->Frames/Cables -> Axial Force)
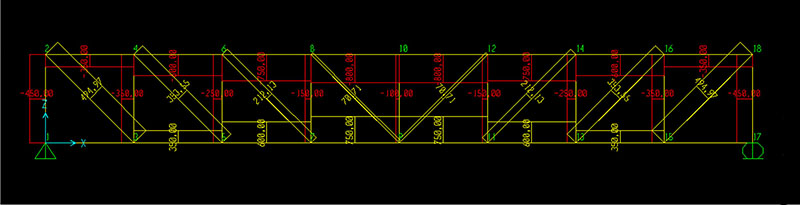
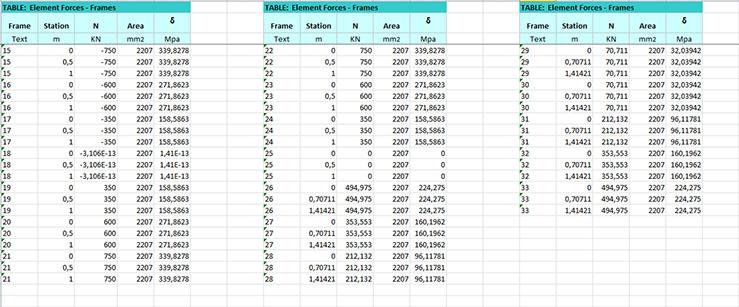
Ora vado a visualizzare le tabelle relative al calcolo della struttura (Display -> Show Tables -> [Joint Output; Element Output; Structure Output] -> Element Forces/Frames) poi esporto la tabella in Excel (File -> Export Current Table -> To Excel) la pulisco dai valori nulli di taglio e momento lasciando solo gli sforzi normali (KN), l'area della sezione del tubolare (mm2) ed il valore di sigma (Mpa)
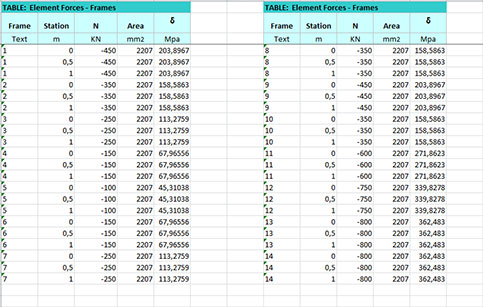
sulla seconda metà consentendomi di disegnare il diagramma dello sforzo normale di tutta
la trave reticolare
A questo punto ho tutti gli sforzi normali di metà trave che si ripeteranno simmetricamente
sulla seconda metà consentendomi di disegnare il diagramma dello sforzo normale di tutta
la trave reticolare
A questo punto ho tutti gli sforzi normali di metà trave che si ripeteranno simmetricamente
sulla seconda metà consentendomi di disegnare il diagramma dello sforzo normale di tutta
la trave reticolare
- N68*l - 9/2 F*3l + F*6l = 0 N68 = - 15/2 F
- N68*l - 9/2 F*3l + F*6l = 0 N68 = - 15/2 F
- N68*l - 9/2 F*3l + F*6l = 0 N68 = - 15/2 F
+ N13*l = 0 N13 = 0 (asta scarica)
+ N23 2 /2 - 7/2 F = 0 N23 = 7 2 /2 F
- N68*l - 9/2 F*3l + F*6l = 0 N68 = - 15/2 F
+ N57*l - 9/2 F*2l + F*3l = 0 N57 = 6 F
+ N67 2 /2 - 15/2 F + 6 F = 0 N67 = 3 2 /2 F
- N810*l - 9/2 F*4l + F*10l = 0 N810 = - 8 F
+ N79*l - 9/2 F*3l + F*6l = 0 N79 = 15/2 F
+ N89 2 /2 + 15/2 F - 8 F = 0 N89 = 2 /2 F- N24*l - 9/2 F*l + F*l = 0 N24 = - 7/2 F
+ N13*l = 0 N13 = 0 (asta scarica)
+ N23 2 /2 - 7/2 F = 0 N23 = 7 2 /2 F
- N68*l - 9/2 F*3l + F*6l = 0 N68 = - 15/2 F
+ N57*l - 9/2 F*2l + F*3l = 0 N57 = 6 F
+ N67 2 /2 - 15/2 F + 6 F = 0 N67 = 3 2 /2 F
- N810*l - 9/2 F*4l + F*10l = 0 N810 = - 8 F
+ N79*l - 9/2 F*3l + F*6l = 0 N79 = 15/2 F
+ N89 2 /2 + 15/2 F - 8 F = 0 N89 = 2 /2 F
- N24*l - 9/2 F*l + F*l = 0 N24 = - 7/2 F
+ N13*l = 0 N13 = 0 (asta scarica)
+ N23 2 /2 - 7/2 F = 0 N23 = 7 2 /2 F
- N68*l - 9/2 F*3l + F*6l = 0 N68 = - 15/2 F
+ N57*l - 9/2 F*2l + F*3l = 0 N57 = 6 F
+ N67 2 /2 - 15/2 F + 6 F = 0 N67 = 3 2 /2 F
- N810*l - 9/2 F*4l + F*10l = 0 N810 = - 8 F
+ N79*l - 9/2 F*3l + F*6l = 0 N79 = 15/2 F
+ N89 2 /2 + 15/2 F - 8 F = 0 N89 = 2 /2 F- N24*l - 9/2 F*l + F*l = 0 N24 = - 7/2 F
+ N13*l = 0 N13 = 0 (asta scarica)
+ N23 2 /2 - 7/2 F = 0 N23 = 7 2 /2 F
- N68*l - 9/2 F*3l + F*6l = 0 N68 = - 15/2 F
+ N57*l - 9/2 F*2l + F*3l = 0 N57 = 6 F
+ N67 2 /2 - 15/2 F + 6 F = 0 N67 = 3 2 /2 F
- N810*l - 9/2 F*4l + F*10l = 0 N810 = - 8 F
+ N79*l - 9/2 F*3l + F*6l = 0 N79 = 15/2 F
+ N89 2 /2 + 15/2 F - 8 F = 0 N89 = 2 /2 F
+ N13*l = 0 N13 = 0 (asta scarica)
+ N23 2 /2 - 7/2 F = 0 N23 = 7 2 /2 F
- N68*l - 9/2 F*3l + F*6l = 0 N68 = - 15/2 F
+ N57*l - 9/2 F*2l + F*3l = 0 N57 = 6 F
+ N67 2 /2 - 15/2 F + 6 F = 0 N67 = 3 2 /2 F
- N810*l - 9/2 F*4l + F*10l = 0 N810 = - 8 F
+ N79*l - 9/2 F*3l + F*6l = 0 N79 = 15/2 F
+ N89 2 /2 + 15/2 F - 8 F = 0 N89 = 2 /2 F
- N24*l - 9/2 F*l + F*l = 0 N24 = - 7/2 F
+ N13*l = 0 N13 = 0 (asta scarica)
+ N23 2 /2 - 7/2 F = 0 N23 = 7 2 /2 F
- N68*l - 9/2 F*3l + F*6l = 0 N68 = - 15/2 F
+ N57*l - 9/2 F*2l + F*3l = 0 N57 = 6 F
+ N67 2 /2 - 15/2 F + 6 F = 0 N67 = 3 2 /2 F
- N810*l - 9/2 F*4l + F*10l = 0 N810 = - 8 F
+ N79*l - 9/2 F*3l + F*6l = 0 N79 = 15/2 F
+ N89 2 /2 + 15/2 F - 8 F = 0 N89 = 2 /2 F
su tre aste per analizzarne lo sforzo normale
Grazie al metodo di Ritter opero una sezione
su tre aste per analizzarne lo sforzo normaleGrazie al metodo di Ritter opero una sezione
Grazie al metodo di Ritter opero una sezione
su tre aste per analizzarne lo sforzo normale
Grazie al metodo di Ritter opero una sezione
su tre aste per analizzarne lo sforzo normale
Grazie al metodo di Ritter opero una sezione
su tre aste per analizzarne lo sforzo normale
Commenti recenti