Blog

Dimensionamento di un sistema con travi Vierendeel

L’obiettivo dell’esercitazione è quello di modellare un aggetto con una Vierendeel e verificare gli effetti conseguenti su travi e pilastri.

1. Definizione del modello                                                                                                                                     

La struttura in cemento armato è composta da tre travi Vierendeel, ognuna delle quali ha un estremo libero e l’altro incastrato nel setto corrispondente. Ogni trave Vierendeel è scandita in cinque moduli da 3.50 m x 3.50 m, mentre il setto ha dimensioni 10,50 m x 7,00 m.

Dopo aver stabilito la geometria del modello, si rappresenta la struttura su SAP2000, realizzando il setto con una poly area, successivamente discretizzata in superfici da 0,25 x 0,25 m.

 

2. Assegnazione dei vincoli                                                                                                                                   

Si assegnano come vincoli a tutti i punti base del setto gli incastri, in modo che il comportamento del setto sia assimilabile a quello reale.

 

3. Assegnazione dei carichi                                                                                                                                   

Data la geometria della struttura, si stabilisce il carico in base alle aree di influenza, determinando le forze concentrate F sui pilastri.

-Pilastri perimetrali F= -173.35 kN

-Pilastro perimetrale (estremo libero) F= -86.67 kN

-Pilastri centrali F= -315.41 kN

-Pilastro centrale (estremo libero) F= -157.70 kN

4. Assegnazione delle sezioni                                                                                                                               

La sezione del setto è in cemento armato ed è definita tramite una shell con spessore 0,6 m.

Le travi e i pilastri invece vengono dimensionati tramite la forza F dovuta al carico (pacchetto solaio + peso proprio) e i momenti massimi (sulle travi M=9FL/4, sui pilastri M=FL/2, dove L=3.50 m). Per aumentare la rigidezza flessionale dei pilastri il momento d’inerzia deve essere maggiore, e quindi bisogna andare ad aumentare la sezione dei pilastri.

 

5. Analisi e verifiche                                                                                                                                               

Fatte tutte le assegnazioni, si procede all’analisi per verificare gli effetti della combinazione di carico allo stato limite ultimo (SLU). Tramite l’analisi si individuano i nuovi momenti flettenti, in questo modo si possono verificare le sezioni precedentemente dimensionate.

 

Per effettuare la verifica degli abbassamenti si sottopone la struttura allo stato limite di esercizio (SLE), quindi a nuove forze concentrate sui pilastri. Il nodo sottoposto ad un abbassamento maggiore è quello nell’estremo libero della trave Vierendeel centrale, di conseguenza si verifica che l’abbassamento massimo sia inferiore a 1/200 della luce (17.50 m / 200): δ_max = 0,0182 m < 0.0857 m OK

La quarta esercitazione si poneva come obiettivo il dimensionamenti di una Trave Vierendeel. Si è partiti immaginando una struttura formata da due setti in cls armato di base 8 m e altezza 12 m, ai quali vengono incastrate due travi Vierendeel che aggettano di 16 m, con una maglia quadrata di 4 m e altezza 3 m.

Analizzando i carichi che gravano sulle travi risulta un valore di Qu 12,23 KN/m derivante dal calcolo allo SLU tra qs=3,62 kN/mq, qp=2,81 kN/mq e qa=2kN/mq considerando un solaio come specificato in foto:

A questo punto si è disegnato il il modello su Autocad e successivamente importato su SAP, inseriti i vincoli e le relative forze si procede all'analisi e si esportano i dati utili su Excel. Nei valori si ricercano N e M massimi per effetturare il predimensionamento delle sezioni dei montanti, dei  montanti esterni e dei correnti delle travi Vierendeel. Per fare ciò si trova il modulo di resistenza necessario attraverso la relazione Wx= Mmax/fyd che fornisce dati utili alla ricerca del profilato sul sagomario. Si è poi proceduto alla sostituzione delle sezioni ricavate su SAP per avviare una nuova analisi al fine di ottenere i valori specifici di momento e normale tenendo conto del peso proprio della struttura.

Grafico della deformata.

Grafico dello sforzo normale.

 

Grafico del momento.

I nuovi valori sono stati inseriti nelle tabelle Excel per la verifica a pressoflessione di correnti e montanti. Gli elementi risultano inizialmente verificati ad eccezione dei correnti per i quali si sceglie un profilato leggermente più grande che risulterà poi verificato. 

Una volta verificate le sezioni e corrette sul modello di SAP si è effettuato il cpntrollo degli spostamenti considerando che lo spostamento massimo non superi mai 1/200 l max= 16/200=0.08 m. Essendo δ max= 0.0589 m la struttura risulta verificata.

 

Il nostro progetto è caratterizzato da da un sistema di travi Vierendeel a sbalzo per circa 16mt. 

La struttura particolare si sviluppa si 5 piani. La distanza tra i solai è di 4.2mt

Impostata l'analisi dei carichi:

Abbiamo sviluppato l'analisi dei carichi utile per la modellazione successiva in SAP:

  

Importato il modello 3D modellato precedentemente su Autocad abbiamo proseguito con la modellazione:

Apportati i carichi calcolati, una volta avviata l'analisi, sono stati definiti gli schemi statici:

Taglio

Sforzo Assiale:

Momento:

Laboratorio di Progettazione Strutturale 1M – Prof. Ginevra Salerno

Esercitazione 4: Dimensionamento di massima di una trave Vierendeel

Studenti: Patryk Rynkowski, Luca Santilli

Questa esercitazione ha l’obiettivo di dimensionare una trave Vierendeel per risolvere una struttura in aggetto. La trave Vierendeel è caratterizzata da collegamenti rigidi e presenta sollecitazioni di taglio e momento flettente.

Disegniamo quindi una struttura ipotetica con gli estremi di sinistra incastrati ad un supporto esterno e quelli di destra liberi. La lunghezza complessiva è di 23.5m, con interassi da 4.25m, altezza di 12.6m.

Pianta:

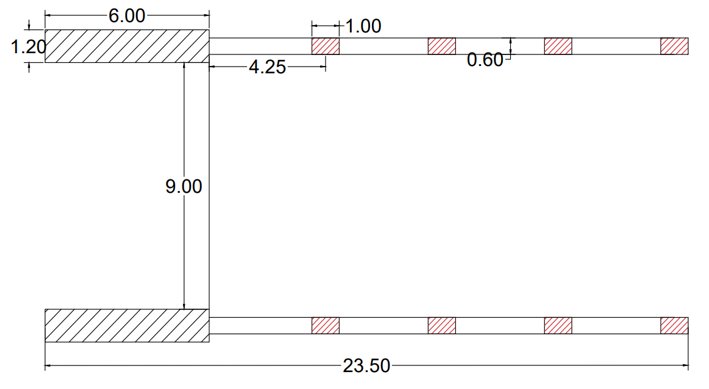
Prospetto:

Dato che la trave Virendeel è assimilabile alla configurazione di un telaio di tipo Shear ruotato di 90⁰, possiamo delineare la deformata del nostro modello.

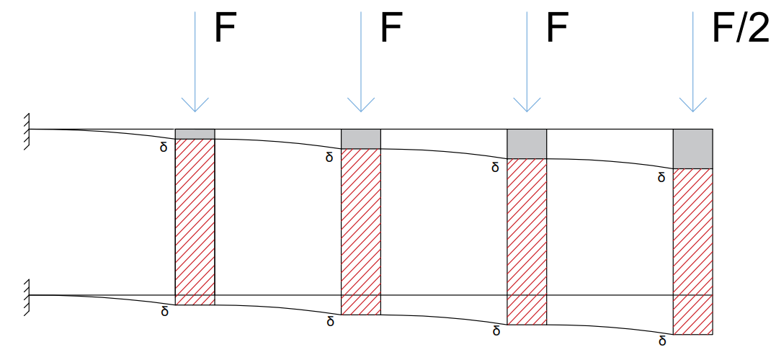
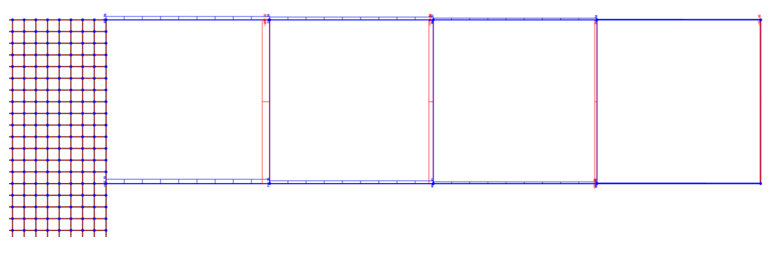
A questo punto passiamo su SAP e modelliamo la struttura tramite il comando Draw Poly Area.

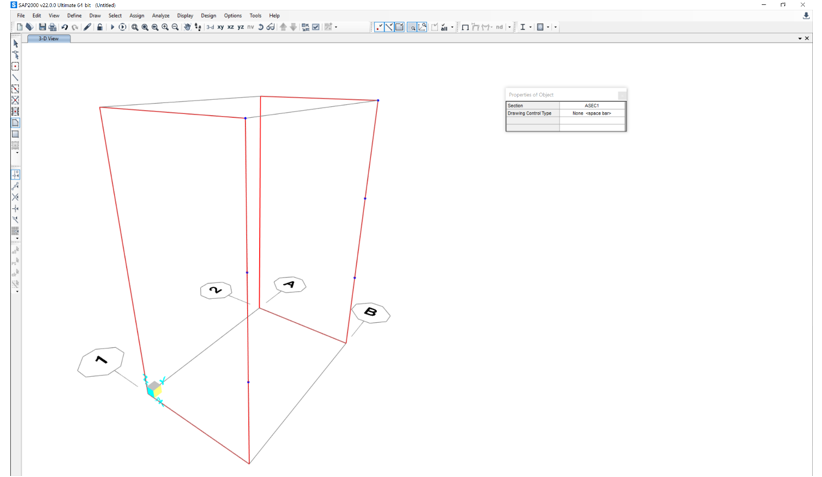
Tramite il comando Edit Area – Divide Area, creiamo una griglia di 0,3mx0,3m.

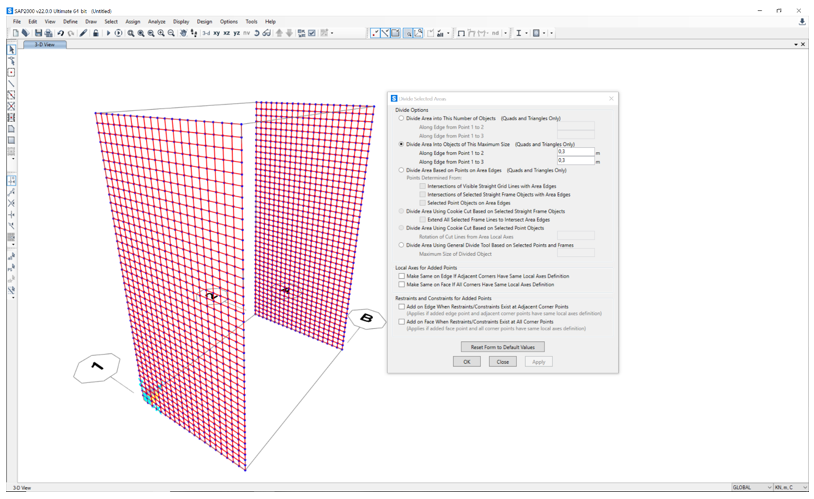
Ora costruiamo la trave Virendeel, appoggiandola ai setti.

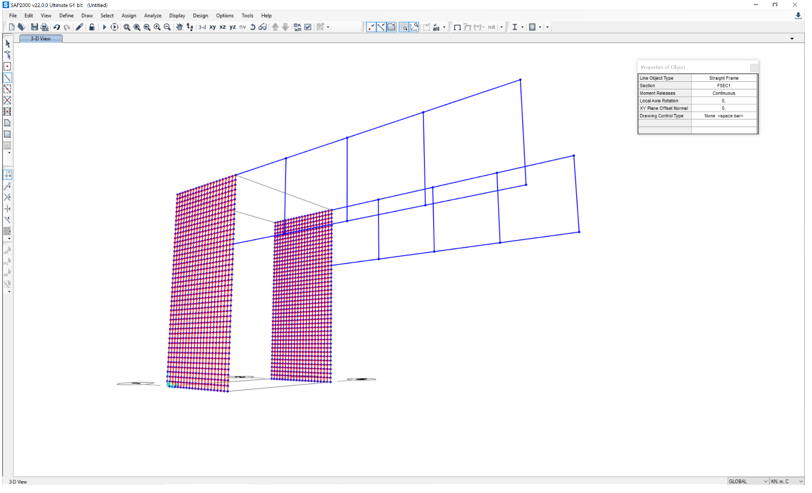
Aggiungiamo ora i vincoli esterni alla base dei setti (Joint Restraints).

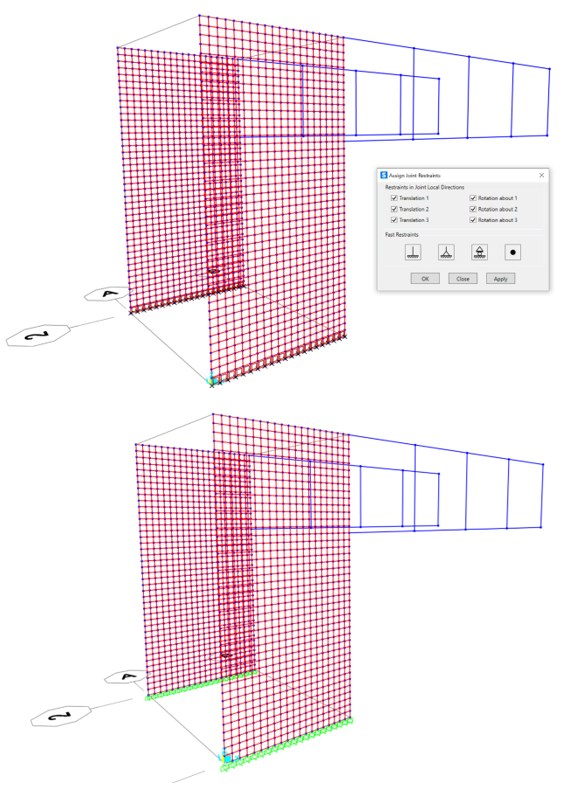
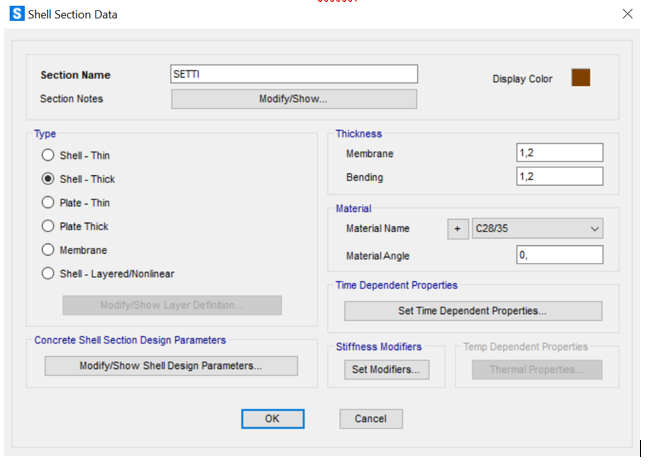
Definiamo la sezione dell’area: 

tipo (Shell-Thick); 

materiale (C28/35); 

spessore (1,2m).

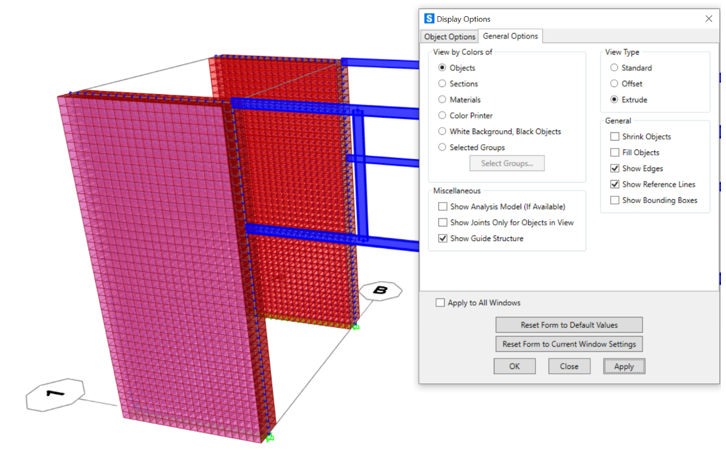
Infine definiamo le sezioni di travi (30x60) e pilastri (100x60): 

PILASTRI

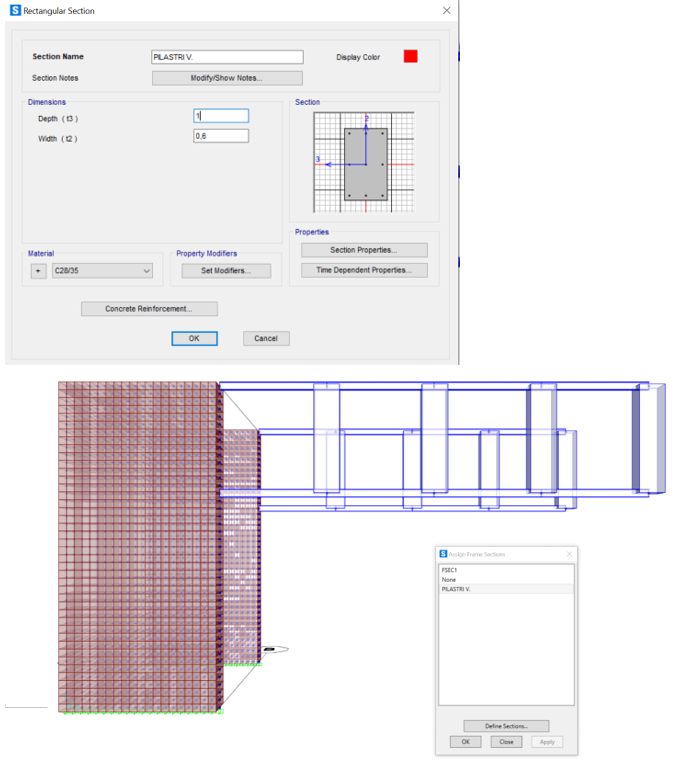
TRAVI

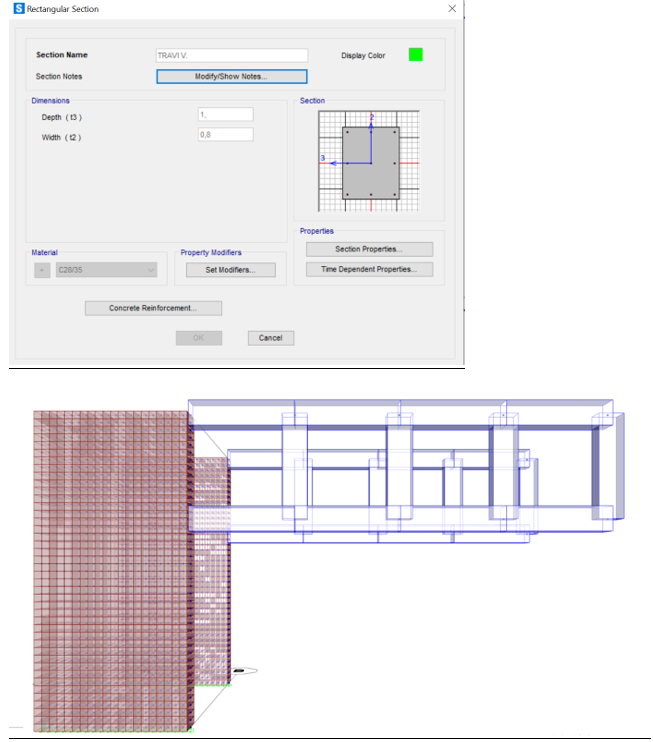
Ora passiamo all’assegnazione dei carichi.

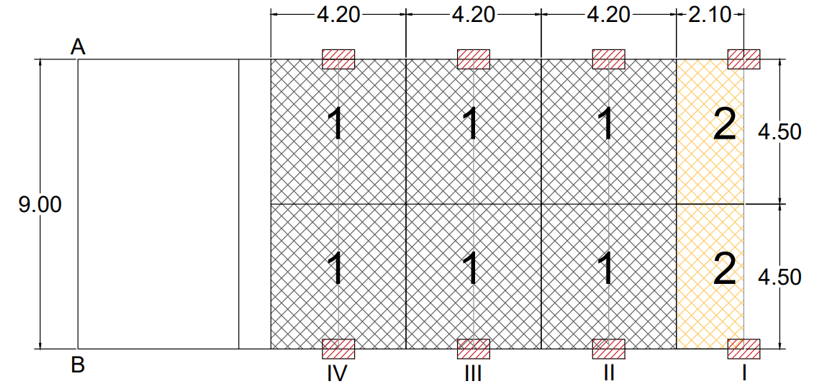
Qs = 3,5 Kn/m²        Qa = 2,00 Kn/m²         Qp = 3,0 Kn/m²        Qu = 12,05 Kn/m²

 

1. Ai = 18,9 m²   q solaio = 227,74 Kn x 2
2. Ai = 9,45 m²   q solaio = 113,87 Kn x 2  

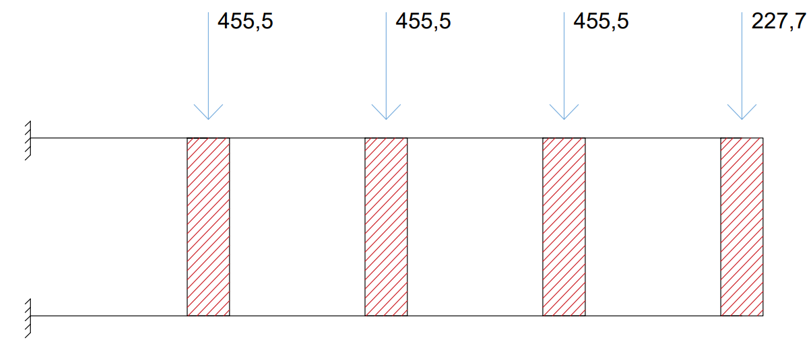
F = 455,5 Kn   F/2 = 227,7  Kn

Assegniamo il tutto su SAP (Assign Joint Forces).

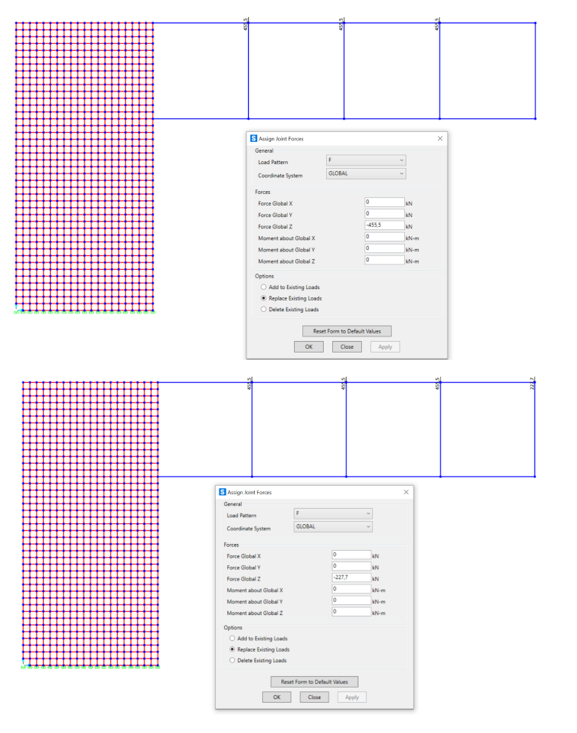
TAGLIO

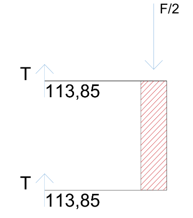
Trave I: 2T = F/2 --> T = F/4 --> T = 113, 85 Kn

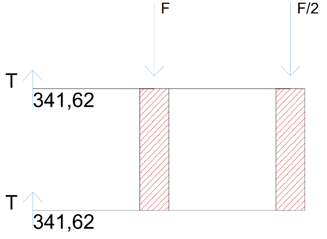
Trave II: 2T = F + F/2 --> T = ¾ F --> 341, 62 Kn

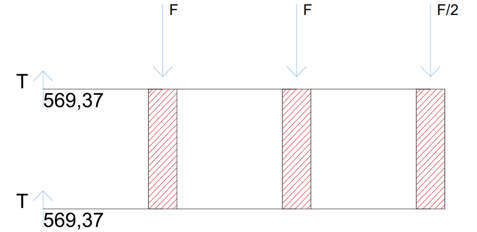
Trave III: 2T = F/2 + F + F = T = 5/4 F --> 569,37 Kn

Trave IV: 2T = F +F + F + F/2 --> 7/4 F      T = 797,12 Kn

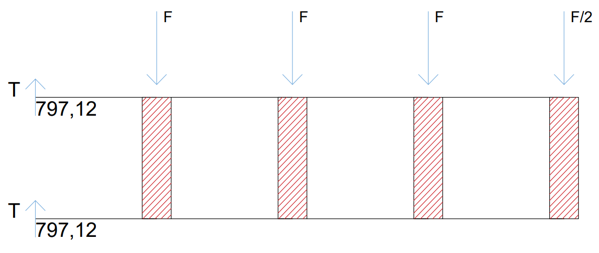
Visualizziamo il grafico del taglio su SAP:

MOMENTO FLETTENTE

M’ = T  ->  M = ∫ T  ->  M = T*X+C

I)  F = 455,5 Kn ; L = 4,2m

M(l) = F/4*4,2+C = 478,27 + C

M(0) = F/4*0+C = C

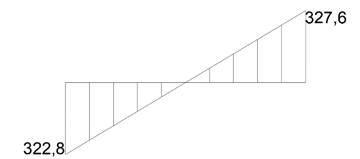
C = M(l) = 478,27 – 327,6 = 150,67

C = M(0) = 150,67

 

II)  F = 455,5 Kn ; L = 4,2m

M(l) = ¾ Fl + C = 1434,82 + C

M(0) = ¾ F*0+C = C

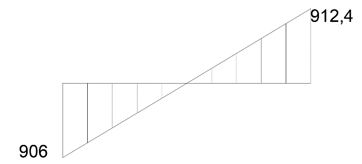
C = M(l) = 1434,82 – 912,4 = 522,42

C = M(0) = 522,42

 

III)  F = 455,5 ; L = 4,2

M(l) = 5/4 F*L+C = 2391,37

M(0) = 5/4 F*0+C = C

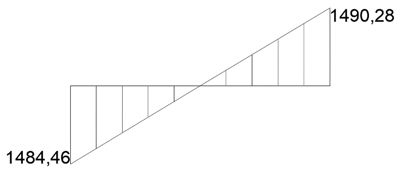
C = M(l) = 2391,37-1490,28 = 901,09

C = M(0) = 901,08

 

IV)  F = 455,5 ; L = 4,2

M(l) = 7/2 F*L+C = 6695,85+C

M(0) = 7/2 F*0+C = C

C = M(l) = 4046,74

C = M(0) = 4046,74

 

Visualizziamo il grafico del momento su SAP:

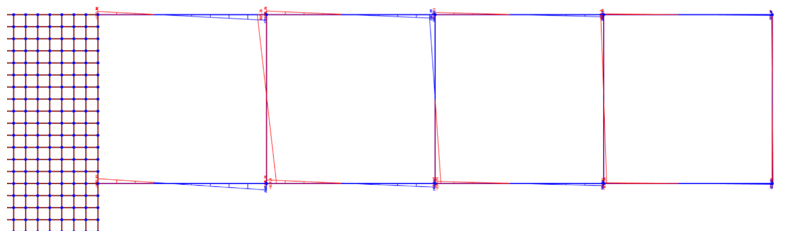
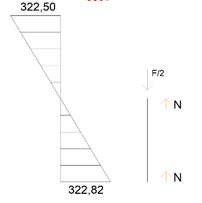
PILASTRI

I) M’ = T   M = 322,82   T = 113,85     

N+N – F/2 = 0

N+N = F/2

2N = F/2 -> N = F/4 -> 111,59

N = 11,59 Kn

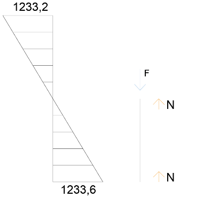
II)  M = 1233,6 Kn    T = 341,62 Kn

N+N-F -> N+N = F -> 2N = F

N = F/2 -> 616,9 Kn

III)  T = 568,37 KnM = 2396,9

N = F/2 -> 1198,45 Kn

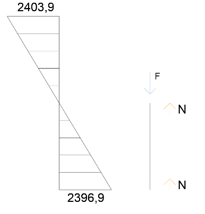
IV)  M = 4139,4   T = 797,12 Kn

N+N = F -> N = F/2 -> 2069,7 Kn

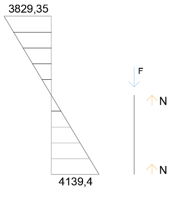
Diagramma sforzo normale N:

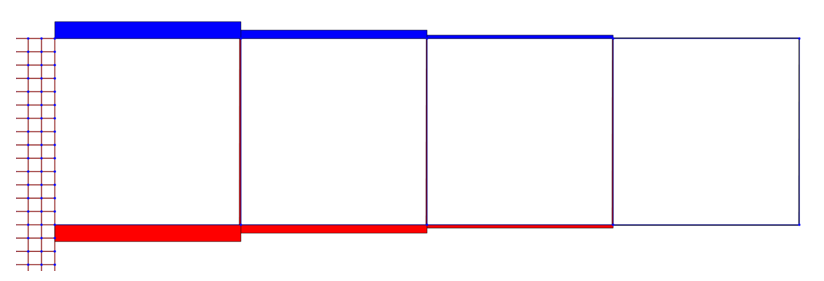
Visualizziamo la struttura deformata su SAP e constatiamo l’ABBASSAMENTO:

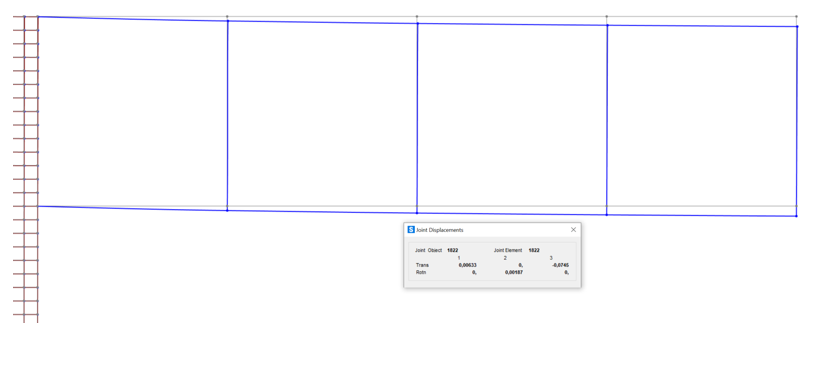
A questo punto possiamo procedere alle verifiche sulle relative tabelle Excel:

PILASTRI:

TRAVI:

Render:

Gruppo: Panella Giordana, Quagliani Ilaria

Il nostro progetto al terzo e quarto piano si compone di due vierendeel di modulo 3x3 m lunghe 18 metri che permettono di avere uno spazio al piano terra senza appoggi. Le vierendeel si appoggiano a due setti disposti longitudinalmente di lunghezza 4 metri e spessore 30 cm.

Pianta Vierendeel                                     

Prospetto

Pianta telaio

ANALISI DEI CARICHI

Solaio

Combinazione di carico allo stato limite ultimo SLU:  qu= 25,96 KN/m

Qu: 25,96 x 3 = 77,88 KN

Sapendo che il cemento armato pesa molto abbiamo aggiunto il peso proprio della struttura: pp = 30,68 KN

Il carico totale applicato puntualmente su ogni nodo è:  F= (77,88 + 30,68) x 3= 325,68 KN

ANALISI STATICA DELLA TRAVE VIERENDEEL

Poiché la trave vierendeel si comporta come un telaio shear type ribaltato  i correnti hanno le stesse caratteristiche dei pilastri del telaio e i montanti quelle del traverso.

In virtù di ciò siamo riuscite a calcolare deformata, taglio e momento dei correnti:

questi sono i diagrammi che ci aspettiamo poi usciranno dall'analisi su sap

MODELLO SU SAP

Su sap sono state applicate le sezioni alle travi, di 30 x 40, e ai pilastri, 30 x 80. Le travi che collegano le vierendeel sono di 25 x 30. La classe del cls scelta è C28/35.

Il modello teorico della trave di Vierendeel è assimilabile a quella del telaio shear type infatti applichiamo rigidezza infinita al pilastro modificando il fattore moltiplicativo del momento d’inerzia.

Applichiamo i carichi definiti in precedenza e i vincoli. Per assicurarci che tra la trave e il setto ci fosse effettivamente un nodo rigido è stato applicato il Constraint Body.

Mandata l'analisi abbiamo ottenuto quello che ci aspettavamo:

Deformata

Taglio

Momento

Sforzo Assiale

VERIFICA

Una volta ricavati i sforzi abbiamo verificato i pilastri a presso flessione e le travi a flessione:

 

 

 

 

 

 

 

Per questa esercitazione si è dimensionata una trave tipo Vierendeel. Si è ipotizzata una struttura formata da 3 setti a cui sono incastrate altrettante travi Vierendeel che aggettano di 15 m, con una maglia quadrata di lato 3 m.

Dall'analisi dei carichi è risultato un valore di Qu 12,23 KN/m che deriva dal calcolo allo SLU tra qs=3,62 kN/mq, qp=2,81 kN/mq e qa=2kN/mq considerando un solaio formato da pannello in gessofibra, trave in acciaio, lamiera grecata, solaio in cls, isolante acustico, massetto e pavimentazione.

A questo punto si è disegnato il il modello su CAD ed importato su SAP da cui si sono rilevati i valori di N e M massimi per effetturare il predimensionamento delle sezioni dei dei montanti e dei correnti, centrali e di bordo, delle Vierendeel. Per fare ciò si trova il modulo di resistenza necessario attraverso la relazione Wx= Mmax/fyd per poi trovare i profili nel sagomario. A questo punto si sono sostitute le sezioni ricavate su SAP per avviare di nuovo l'analisi al fine di ottenere i nuovi valori di momento e normale tenendo conto del peso proprio della struttura.

Grafico dello sforzo normale.

Grafico del momento.

I nuovi valori sono stati inseriti nelle tabelle excel per la verifica a pressoflessione di correnti e montanti. Risultano verificati tutti gli elementi ad eccezione dei correnti delle Vierendeel esterne per le quali non basta un profilato HEA320. Il corrente, quindi, risulta verificato con un profilato leggermete più grande, un HEA360.

Infine si è verificato se l'abbassamento fosse minore di 1/200 della luce totale, ovvero 15/200=0,075 m. Lo spostamento è di 0.054 m. La verifica risulta soddisfatta.

 

L’esercitazione prevede il dimensionamento di massima e la verifica di una trave Vierendeel costituita da una serie di travi continue, caratterizzate da un’infinita rigidezza flessionale, e una serie di montanti verticali infinitamente rigidi sia assialmente che flessionalmente. Abbiamo ipotizzato tre travi Vierendeel composte ciascuna da quattro campate di 3,50x3,50 m e  poste ad un interasse di 5,00 m l’una dall’altra. Poiché il modello ideale semplificato di trave Vierendeel è assimilabile ad un telaio shear – type ruotato di 90° possiamo risolvere la statica della struttura. 

---

Per quanto riguarda l’analisi dei carichi abbiamo fatto riferimento al dimensionamento effettuato per la prima esercitazione di un solaio in laterocemento con destinazione ad uso uffici, tenendo in considerazione la combinazione fondamentale di carico allo SLU con coefficienti parziali di sicurezza sfavorevoli.

q_u= γ_G1 x G₁ + γ_G2 x G₂ + γ_Q2 x Q₁= 1,3 x 1,70 + 1,5 x 3,40 + 1,5 x 2,00 =10,30 kNm^-2

Per ottenere i valori delle forze concentrate agenti sui singoli pilastri moltiplichiamo il carico uniformemente distribuito appena calcolato per l’interasse tra i pilastri e per la loro luce. 

---

A questo punto predimensioniamo i correnti e i pilastri delle Vierendeel e le travi secondarie. 

---

Andiamo ad impostare la struttura su Sap: modelliamo la geometria delle travi Vierendeel e assegniamo i diaphragm constraints a tutti i nodi affinchè abbiano il comportamento di nodi rigidi. Modelliamo poi i setti come gusci con comportamento membranale, vincolati alla base e nel punto di collegamento con le Vierendeel da degli incastri. A questo punto assegniamo le sezioni predimensionate alle travi e ai pilastri utilizzando un calcestruzzo C28/35. 
Assegniamo quindi i carichi puntiformi precedentemente calcolati in corrispondenza dei pilastri. 

 

 

 

 

 

 

 

 

Facciamo quindi partire l’analisi per ricavare i diagrammi e i valori delle sollecitazioni agenti sulla struttura.
Risulta inoltre che i valori del taglio e del momento calcolati risolvendo la statica risultano, seppur approssimati, corrispondenti con quelli determinati da Sap.

---

A questo punto esportiamo le tabelle delle sollecitazioni e procediamo alla verifica degli elementi strutturali: verifichiamo che la tensione agente sulle travi inflesse e sui pilastri pressoflessi sia minore della tensione di rottura. 

La struttura risulta interamente verificata.

---

Effettuiamo ora una verifica di deformabilità per assicurarci che l’abbassamento della struttura sottoposta al carico sia minore di quello massimo ammissibile. 
Calcoliamo quindi il carico allo SLE considerando una combinazione di carico frequente: 
q_e= G₁ + G₂ + ψ_1j x Q₁= 1,70 + 3,40 + 0,5 x 2,00 = 6,1 kNm^-2 
Calcoliamo quindi le deformazioni utilizzando le formule ricavate in precedenza dalla rigidezza traslante della trave, che mette in relazione forza e spostamento.

Risulta che l'abbassamento totale della struttura rispetta i limiti di normativa.

Studentesse: Santacesaria Elena,Schettini Benedetta.

Abbiamo ipotizzato un sistema composto da 3 travi Vierendeel incastrate  su 3 setti.

La trave si compone di 5 campate di 4 metri ciascuna per 4 metri di altezza. Il setto ha dimensioni 6x12x0,5 m

ANALISI DEI CARICHI

L’analisi dei carichi ci ha permesso di calcolare il valore delle forze Normali agenti sui montanti.

Abbiamo calcolato il Qslu di un solaio in laterocemento tramite la somma dei carichi strutturali, sovraccarichi permanenti non strutturali e carichi accidentali per un edificio di uffici aperto al pubblico.

Qs = 2,8  KN/mq

Qp = 3,12  KN/mq

Qa = 3  KN/mq

Qu = 12,91 KN/mq

ANALISI STATICA

TAGLIO

Abbiamo calcolato i valori del taglio e gli spostamenti δ tramite le equazioni di equilibrio.

MOMENTO

Tramite i valori del taglio abbiamo calcolato i Momenti che si sviluppano su ogni tratto di trave.

EQUILIBRIO

AREE DI INFLUENZA

Abbiamo calcolato il carico che grava su ogni montante tramite le aree di influenza e il carico Qslu.

PREDIMENSIONAMENTO

Essendo la Vierendeel un sistema strutturale che simula il comportamento del modello Shear Type in orizzontale, occorre dimensionare i montanti con una rigidezza flessionale maggiore di quella dei correnti, per fare ciò, non possiamo aumentare infinitamente il valore del modulo di elasticità (per arrivare al comportamento del modello teorico), ma possiamo aumentarne la sezione agendo quindi sul momento di inerzia e di conseguenza sulla rigidezza.

Con i valori degli sforzi interni abbiamo effettuato un predimensionamento degli elementi che costituiscono la trave.

Abbiamo predimensionato i correnti a flessione e i montanti a pressoflessione.

COSTRUZIONE DEL MODELLO

Abbiamo costruito la trave Vierendeel su Sap2000, con le dimensioni stabilite, per poi passare alla modellazione dei setti tramite lo strumento Draw Poly Area, ne abbiamo discretizzato la superficie e posto i vincoli di incastro a terra e vincolato la trave Vierendeel ai setti.

Il setto si comporta come una Shell, dunque abbiamo assegnato a questo elemento il suo spessore.

Define > Section Properties > Area Sectiones > Shell > Add new section > Shell Thick > Thickness =0,50

 Il materiale assegnato è lo stesso cls utilizzato per la trave, ovvero il C40/50.

Il passaggio successivo è stata l’assegnazione dei carichi, abbiamo creato quindi un load pattern con i carichi del solaio allo Slu e li abbiamo assegnati ad ogni montante.

Essendo la struttura in cls abbiamo considerato il peso proprio del sistema Vierendeel-setti e abbiamo creato una load combination Qtot comprensiva del peso proprio e del Qslu.

Abbiamo avviato l’analisi per visualizzare la configurazione deformata e i diagrammi delle sollecitazioni.

Diagramma Normale

Diagramma Taglio 2-2

Diagramma taglio 3-3

Diagramma momento 2-2

Diagramma momento 3-3

A questo punto abbiamo estrapolato le tabelle Excel ed effettuato la verifica tramite il valore massimo di Momento,Taglio e Normale.

Le sezioni preassegnate risultano non verificate, dunque ne abbiamo aumentato le dimensioni.

VERIFICA SPOSTAMENTI

Abbiamo calcolato la somma degli spostamenti dei singoli tratti per verificare che non superi il valore massimo di abbassamento.

Sapendo che il valore trovato è stato calcolato con i carichi allo Slu, abbiamo corretto il risultato riducendo l’abbassamento del 35%, ossia considerando la combinazione di carico allo Sle, ottenendo così uno spostmento di 0,038  <  0,08.