Portale di Meccanica

Nella terza esercitazione viene proposta una nuova carpenteria rispetto alla precedente, dovendo tener conto del fatto che non stiamo più lavorando con una trave doppiamente appoggiata, bensì con una mensola. Per quanto rigurda le fasi inizali non ci sono grandi variazioni, poichè il metodo di individuazione dell'area di influenza della trave maggiormente sollecitata rimane identico, così come la riproposizione degli stessi solai e la loro relativa stratigrafia. I materiali usati sono: per il legno Gl 24c, acciaio Fe 430/S275, calcestruzzo C 25/30 con barre d’acciaio B450A.

LEGNO

ACCIAIO

CEMENTO ARMATO

Prima di iniziare l'analisi è bene ricordare che non ci troviamo in presenza di una trave doppiamente appoggiata, ma di una mensola, quindi dobbiamo considerare che  il momento massimo, in corrispondenza della sezione di incastro varrà:

M_max= q_ul²/ 2

A questo punto posso procedere, attraverso l'aiuto di un foglio Excel, al dimensionamento della sezione della trave per ciascuna delle tre tecnologie e la relativa verifica a deformabilità.

LEGNO

Essendo il legno un materiale leggero, posso trascurare il peso proprio della trave.

ACCIAIO

Ipotizzata la struttura in figura, la trave che mi accingo a dimensionare è quella maggiormente sollecitata, ossia quella evidenziata d’arancione, in quanto interessata dalla maggiore area di influenza - 15 m² (dove 3 m = luce, 5 m = interasse).

TRAVE IN LEGNO

1| Analisi dei carichi

I carichi - strutturali, permanenti e accidentali - che la trave dovrà sopportare sono gli stessi dell'Esercitazione 2.

      q_s = 0,438 kN/m²

      q_p = 2,69 kN/m²

      q_a = 5,00 kN/m²

**Carico totale

A questo punto, tramite il foglio di calcolo – Excel (scaricabile dalla sezione Download del Portale di Meccanica), ricavo il carico totale. Quindi inserisco i valori dell’interasse (5 m), di q_s (0.438 kN/m²), di q_p (2.69 kN/m²) e di q_a (5 kN/m²) e il foglio di calcolo mi fornisce il valore del carico totale q_u, secondo la formula seguente:

      q_u = [(q_s x 1,3) + (q_p x 1,3) + (q_a x 1,5)] x interasse

2| Progetto

Come seconda cosa, servendomi sempre del foglio di calcolo – Excel, inserisco la luce della trave (3 m) e ottengo il momento massimo della stessa – intesa come una mensola, secondo la formula M_max = ql²/2

Poi fornisco i seguenti valori:

• resistenza a flessione caratteristica f_m,k = 24 MPa (dipendente dal tipo di legno, ovvero lamellare GL 24h)
• coefficiente della durata del carico k_mod = 0,8 (fornito dalla normativa)
• coefficiente parziale di sicurezza del materiale γ_m = 1,45 (legno lamellare)

e ottengo la tensione ammissibile f_d [N/mm²], secondo la formula seguente:

      f_d = f_m,k x k_mod / γ_m

Ipotizzo il valore della base b (40 cm) e ricavo l’altezza minima h_min che la trave deve avere, secondo la seguente formula:

      h_min = (interasse x M_max x 1000 / b x f_d) ^ 0,5

Assegno quindi alla sezione una h = 60 cm.

Definisco poi il valore del modulo elastico E = 8000 N/mm², e ottengo il momento d’inerzia I_x, i carichi incidenti q_e, l’abbassamento massimo v_max  e il rapporto tra la luce e l’abbassamento massimo della trave l/v_max, rispettivamente secondo le seguenti formule

      I_x = b x h³ / 12

      q_e = (q_s + q_p + 0.5 x q_a) x i

      v_max = q_e x 10 x (l x 100)⁴ / (8 x E x 100 x I_x)

3| Verifica

A questo punto verifico che il rapporto tra la luce e l’abbassamento massimo della trave sia maggiore o uguale a 250, ossia l/v_max ≥ 250, trascurando il peso proprio della trave a causa della sua leggerezza:

Essendo l/v_max (606.49) > 250 la sezione 40 x 60 cm è verificata.

TRAVE IN ACCIAIO

1| Analisi dei carichi

I carichi - strutturali, permanenti e accidentali - che la trave dovrà sopportare sono gli stessi dell'Esercitazione 2.

      q_s = 2,01 kN/m²

      q_p = 2,84 kN/m²

      q_a = 5,00 kN/m²

**Carico totale

A questo punto, tramite il foglio di calcolo – Excel, ricavo il carico totale. Quindi inserisco i valori dell’interasse (5 m), di q_s (2.01 kN/m²), di q_p (2.84 kN/m²) e di q_a (5 kN/m²) e il foglio di calcolo mi fornisce il valore del carico totale q_u, secondo la formula seguente:

      q_u = [(q_s x 1,3) + (q_p x 1,3) + (q_a x 1,5)] x interasse

2| Progetto

Come seconda cosa, servendomi sempre del foglio di calcolo – Excel, inserisco la luce della trave (3 m) e ottengo il momento massimo della stessa – intesa come una mensola, secondo la formula M_max = ql²/2

Poi fornisco il seguente valore:

• tensione di snervamento f_y,k = 275 MPa (dipendente dal tipo di acciaio, ovvero Fe 430/ S275)

e ottengo il modulo di resistenza elastico minimo W_x,min [cm³], secondo la formula seguente:

      W_x,min = M_max / f_d x 1000

Quindi, sul sagomario, scelgo il profilo IPE 450 con W_x = 1500 cm³, I_x = 33740 cm⁴ e peso = 77.6 kg/m = 0.776 kN/m e ottengo q_e, secondo la seguente formula:

      q_e = (q_s + q_p + 0.5 x q_a) x i + p_trave

Infine definisco il valore del modulo elastico E = 210000 N/mm², e il foglio di calcolo mi fornisce il valore dell’abbassamento massimo v_max e il suo rapporto con la luce l/v_max, rispettivamente secondo le formule seguenti:

      v_max = q_e x 10 x (l x 100)⁴ / (8 x E x 100 x I_x)

3| Verifica

A questo punto verifico che il rapporto tra la luce e l’abbassamento massimo della trave sia maggiore o uguale a 250, ossia l/v_max ≥ 250.

Essendo l/v_max (559.446) > 250 il profilo IPE 450 è verificato.

TRAVE IN CALCESTRUZZO ARMATO

1| Analisi dei carichi

I carichi - strutturali, permanenti e accidentali - che la trave dovrà sopportare sono gli stessi dell'Esercitazione 2.

      q_s = 2,368 kN/m²

      q_p = 2,654 kN/m²

      q_a = 5,00 kN/m²

**Carico totale

A questo punto, tramite il foglio di calcolo – Excel, ricavo il carico totale. Quindi inserisco i valori dell’interasse (5 m), di q_s (2.368 kN/m²), di q_p (2.654 kN/m²) e di q_a (5 kN/m²) e il foglio di calcolo mi fornisce il valore del carico totale q_u, secondo la formula seguente:

      q_u = [(q_s x 1,3) + (q_p x 1,3) + (q_a x 1,5)] x interasse

2| Progetto

Come seconda cosa, servendomi sempre del foglio di calcolo – Excel, inserisco la luce della trave (3 m) e ottengo il momento massimo della stessa – intesa come una mensola, secondo la formula M_max = ql²/2

Poi fornisco il seguente valore:

• tensione di snervamento dell’acciaio f_yk = 450 MPa (dipendente dal tipo di acciaio, ovvero B450C)

e ottengo la tensione di progetto dell’acciaio f_yd [MPa], secondo la formula seguente:

      f_yd = f_yk / γ_s, dove γ_s = 1,15

Mentre, per la tensione di progetto del calcestruzzo (cls) f_cd, fornisco la resistenza caratteristica a compressione R_ck (40 N/mm²) e il foglio Excel me lo calcola, secondo la formula seguente:

      f_cd = 0,85 x R_ck / γ_c, dove γ_c = coefficiente parziale di sicurezza = 1,5 

oltre a calcolarmi β (0.46) e r (2.26).

Ipotizzo il valore della base b (40 cm) e ricavo prima l’altezza utile minima h_u,min, secondo la seguente formula:

      h_u,min = r x (M_max x 1000 / (f_cd x b)) ^ 0,5

e poi l’altezza minima H_min, secondo la formula seguente:

      H_min = h_u,min + Δ, dove Δ = copriferro = 5 cm

Assegno quindi alla sezione una H = 50 cm, e il foglio di calcolo mi fornisce q_e secondo la formula seguente:

      q_e = (q_s + q_p + 0.5 x q_a) x i + p_trave

Infine definisco il valore del modulo elastico E = 21000 N/mm² e ottengo il momento d’inerzia I_x, l’abbassamento massimo v_max e il rapporto tra la luce e l’abbassamento massimo l/v_max, rispettivamente secondo le seguenti formule:

      I_x = b x h³ / 12

      v_max = q_e x 10 x (l x 100)⁴ / (8 x E x 100 x I_x)

3| Verifica

A questo punto, come fatto per la trave in legno e in acciaio, verifico che il rapporto tra la luce e l’abbassamento massimo della trave sia maggiore o uguale a 250, ossia l/v_max ≥ 250.

Essendo l/v_max (1594.73) > 250 la sezione 40 x 50 cm è verificata.

INTRODUZIONE: In questa esercitazione dimensioneremo una trave a sbalzo nelle tre principali tecnologie: legcemento armato e acciaio.

Definita la carpenteria di riferimento, individuo la trave maggiormente sollecitata e l'area di influenza di luce L=2,5 m e interasse I=4,55 m (nel rettangolo rosso).

Prendo in considerazione la stratigrafia dei solai utilizzati per il dimensionamento della trave e i carichi trovati.

1_STRUTTURA IN LEGNO

La parte iniziale del procedimento è la stessa applicata nella seconda esercitazione, quindi i risultati di h min,per il legno e il c.a., e di W min,per l'acciaio, saranno gli stessi.

N.B. Differentemente dalla seconda esercitazione, dove prendavamo in considerazione una trave doppiamente appoggiata, ora consideriamo lo schema statico di una mensola, quindi il valore del momento massimo sarà M=ql^2/2.

ANALISI:

qs:  0,51 KN/m^2

qp:  2,54 KN/m^2

qa:  2 KN/m^2

Il foglio Excell mi fornisce il carico totale a metro lineare (qu) e, inserita la luce, il momento massimo Mmax: ql^2/2.

Assumo:

f m.k.=24               (legno lamellare GL 24c)           [resistenza a flessione caratteristica]

k mod=0,80                                                             [coefficiente di durata del carico]

ym=1,50                                                                  [coefficiente parziale di sicurezza del materiale]

Con questi valori il file Excell può calcolarmi la tensione ammissibile fd=(fmk * k mod)/ym.

PROGETTO:

Ipotizzo la base della trave di 25 cm. Il foglio elettronico svilupperà un valore di H min (altezza minima) che richiederà di essere ingegnerizzata a causa della presenza dei decimali.

Assegno al materiale un modulo elastico E=8000 Mpa.

Ottengo:

1. Ix (momento di inerzia) = (b*h^3)/12

2. qe (carico incidente) dove non vi è inserito il peso proprio della trave poichè si tratta di un materiale leggero, a differenza dell'acciao e del cls armato.

Occore fare la verifica a deformabilità controllando che l'abbassamento massimo del profilo, studiato in rapporto con la luce, non sia tale da deformare la struttura, ostacolandone l'uso. Perciò la verifica viene fatta riferendosi allo stato limite di esercizio (SLE).

v max (abbassamento massimo); L (luce)/v max > 250 (valore valido per i solai in generale)

2_STRUTTURA IN CALCESTRUZZO ARMATO

ANALISI:

qs: 2,12 KN/m^2

qp: 1,9 KN/m^2

qa: 2 KN/m^2

Il file Excell mi da qu (carico totale a metro lineare) e M max (momento massimo)=ql^2/2, inserendo prima la luce.

Assumo:

fyk [tensione di snervamento]= 450 Mpa

fck [valore caratteristico di resistenza cilindrica] = 35 Mpa

Con questi valori posso calcolarmi le tensioni di progetto fyd (acciaio) e fcd (cls).

PROGETTO:

Ipotizzo la base della trave uguale a 25 cm e un copriferro sigma = 5 cm. Il foglio elettronico mi da un'altezza minima (hmin) che poi ingegnerizzerò.

Assumo un modulo elastico del materiale E = 8000 Mpa.

Mi trovo:

Ix = (b*h^3)/12

qe = carico incidente, dove inserisco il peso della trave.

v max = abbassamento massimo

L (luce)/ v max > 250

3_STRUTTURA IN ACCIAIO

ANALISI:

qs: 1,78 KN/m^2

qp: 1,81 KN/m^2

qa: 2 KN/m^2

Il file Excell mi da qu (carico totale a metro lineare) e M max (momento massimo)=ql^2/2, inserendo prima la luce.

Assumo:

fyk = 235  ( tensione di snervamento)

Il foglio elettronico mi calcola fd (tensione di progetto) dell'acciao.

PROGETTO:

W min (modulo di resistenza) = M max/fd

Ingegnerizzo il valore di W min.

Ottengo i seguenti valori dalla tabella dei profili IPE standard:

Ix (Jx nella tabella)  [cm^4]

peso [in Kg/m nella tabella, per convertire il valore in KN/m moltiplico per 10^-2]

qe (carico incidente) dove aggiungo il peso della trave

v max = abbassamento massimo

L (luce)/ v max > 250

Disegno il mio impalcato

Individuo la mensola maggiormente sollecitata

Luce 3,00 metri

Interasse 4,00 metri

Area di influenza  data da luce x interasse. Dunque 3,00 x 4,00 = 12 m²

SOLAIO IN ACCIAIO

CARICHI STRUTTURALI

Soletta in cls

0,12 m³/m² x 2100 kg/m³ = 252 kg/m² = 2,46 KN/m²

Travetti

Peso  travetto al m²= 12,9 kg/m x 1,00 m= 12,9 kg/m²=0,126 KN/m²

 Lamiera grecata

HI-BOND TIPO A 55/P 600

10,47 kg/m²= 0,102 kN/m²

Rete elettrosaldata

820/2  AD

4,08 kg/m²= 0,039 kN/m²

CARICHI STRUTTURALI TOTALI  2,72 KN/m²

CARICHI PERMANENTI

Massetto in cls allegerito

0.05 m³/m² x 1800 Kg/m³  = 90 Kg/m² = 0,882 kN/m²

Controsoffitto

0.015 m³/m² x 1325 Kg/m³  = 19,875 Kg/m² = 0,194 kN/m²

Pavimento

Peso specifico = 0.018 m³/m² x 700 Kg/m³  = 12,6 Kg/m² = 0,1223 kN/m²

Incidenza Impianti:

0,5 KN/m²

Incidenza Tramezzi:

1 KN/m²

CARICHI PERMANENTI TOTALI  2,70 KN/m²

CARICHI ACCIDENTALI 3 kN/m^2​

Inserisco tutti i valori trovati nella tabella excel e trovo il carico ultimo e il momento massimo. A differenza dell'esercitazione della trave, trattandosi di una mensola

il momento sarà dato da :

M_max= ql²/8

Scelgo l'acciaio Fe S235 (Fe 360) con tensione caratteristica di snervamento f_yk=235 MPa e trovo  W_x,min 

Cofronto questo valore con le tabelle dei profilati  IPE360

Effettuo la verifica  dell'abbassamento massimo vmax. Inserisco il modulo elastico e calcolo Ix.

Il rapporto tra la luce e il vmax è maggiore di 250, Dunque la sezione scelta è verificata.

SOLAIO CEMENTO ARMATO

CARICHI STRUTTURALI

Getto in cls

0,04 m³/m² x 2100 kg/m³ = 84 kg/m² = 0,82 KN/m²

Travetti

 (0.16 m x 0,10 m x 1,00 m) x 2 = 0,032 m³/m²

0,32 m³/m² x 2100 kg/m³ = 67,2 kg/m² = 0,658 KN/m²

Pignatte

(0,16 m  x 0,40 m x 1,00 m) x 2 = 0.128 m³/m²

0.015 m³/m² x 1500 Kg/m³  = 192 Kg/m² = 1,8 kN/m²

Rete elettrosaldata

815/2  AD

Peso 5,30  kg/m²= 0,052 kN/m²

CARICHI STRUTTURALI TOTALI: 3,33 KN/m²

CARICHI PERMANENTI

Pavimento in cotto

0,025 m  x 1,00 m x 1,00 m = 0.025 m³/m²

Peso specifico = 0.025 m³/m² x 40 Kg/m³  = 1 KN/m²

Massetto

 (0,04 x 1,00 x 1,00) m³/m²  x 1800kg/m³ = 72,0 kg/m² = 0,72 kN/m²

Intonaco

0,015 m  x 1,00 m x 1,00 m = 0.015 m³/m²

0.015 m³/m² x 12 KN/m³ = 0,18 KN/m²

Isolante acustico

Spessore 1,3 cm = 0.013 m

Peso specifico = 0,05 kN/m²

Incidenza Impianti:

0,5 KN/m²

Incidenza Tramezzi:

1 KN/m²

CARICHI PERMANENTI TOTALI: 3,45 KN/m²

CARICHI ACCIDENTALI 3 kN/m^2​

Calcono il carico ultimo e il momento massimo. Scelgo le classi di resistenza e inserisco la base pari a 40 cm. Mi trovo così l'H. Dato che stiamo parlando di cemento armato è importante inserire anche il peso proprio della trave aggiungendolo ai carichi strutturali. 

Inserisco Il modulo elastico e calcolo Ix

Verifico infine che rapporto  Ix/vmax sia maggiore di 250. 

SOLAIO IN LEGNO

CARICHI STRUTTURALI

Travetti

 (0.2 m x 0,10 m x 1,00 m) x 2 = 0,04 m³/m²

0,04 m³/m² x 5 kN/m³ = 0,2 kN/m²

TAVOLATO

(0,03 m  x 1,00 m x 1,00 m) = 0,03 m³/m²

0.03 m³/m² x 5  KN/m³  = 0,15 kN/m²

CARICHI STRUTTURALI TOTALI: 0,35 KN/m²

CARICHI PERMANENTI

Pavimento in legno rovere

0,02 m  x 1,00 m x 1,00 m = 0.02 m³/m²

0.02 m³/m² x 7 KN/m³  = 0,14 KN/m²

Massetto

 (0,04 x 1,00 x 1,00) m³/m²  x 1800kg/m³ = 72,0 kg/m² = 0,72 kN/m²

Incidenza Impianti: 0,5 KN/m²

Incidenza Tramezzi: 1 KN/m²

CARICHI PERMANENTI TOTALI: 2,36 KN/m²

CARICHI ACCIDENTALI  3 kN/m^2​

Inserisco tutti i valori trovati nella tabella excel Trovo il carico ultimo e il momento massimo. 

Deciso il tipo di di legno impiegato GL24h,  inserisco i coeff.   k_mode g_m 

k_mod 0,6

g_m 1,45

Fisso la base di 30 cm e mi trovo l'H. 

Inserisco infine il modulo elastico, calcolo Ix e verifico che il rapporto tra Ix/vmax sia maggiore di 250. 

Disegno il mio impalcato

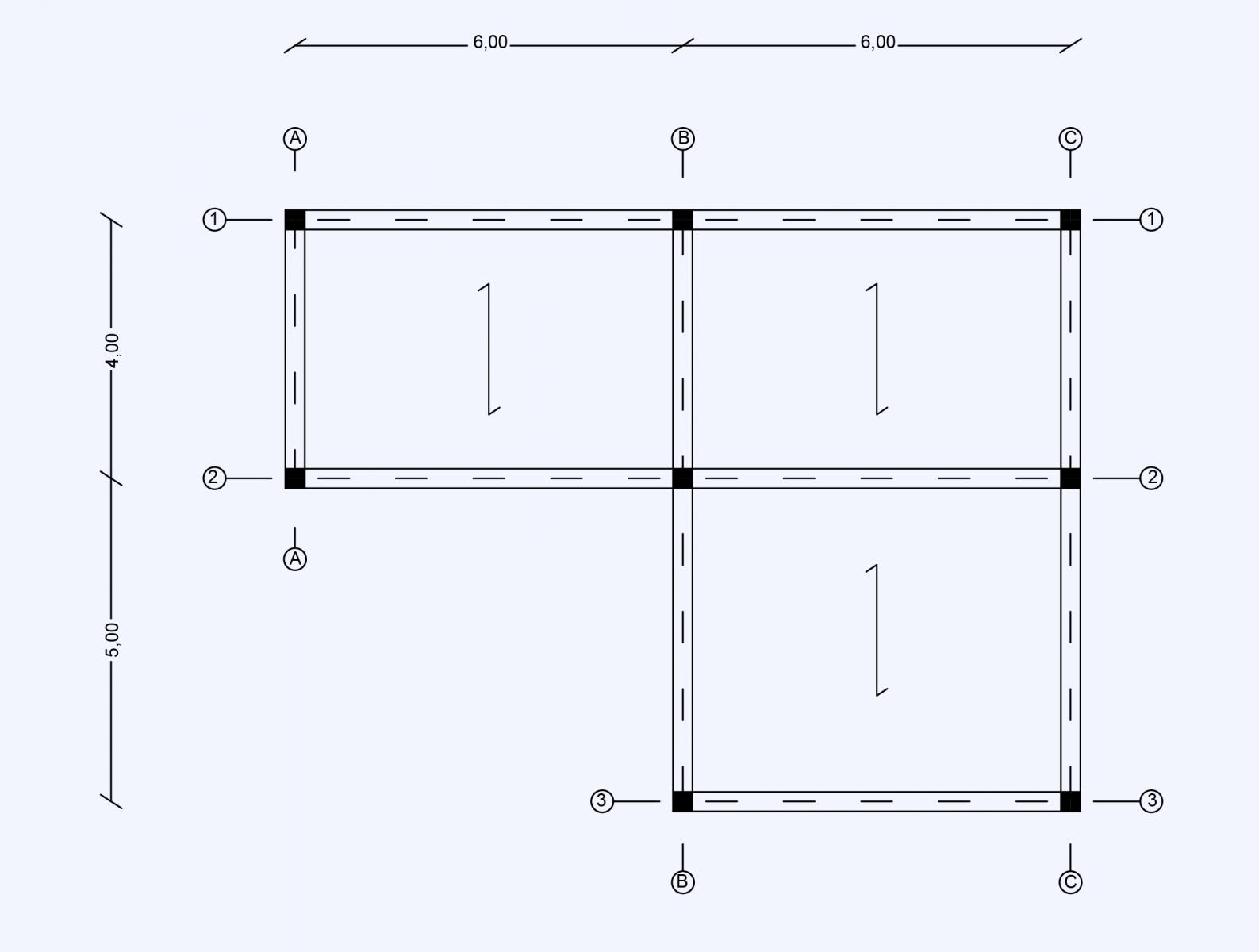
Individuo la trave maggiormente sollecitata

Luce 6,00 metri

Interasse 4,50 metri

Area di influenza  data da luce x interasse. Dunque 6,00 x 4,50 = 27 m²

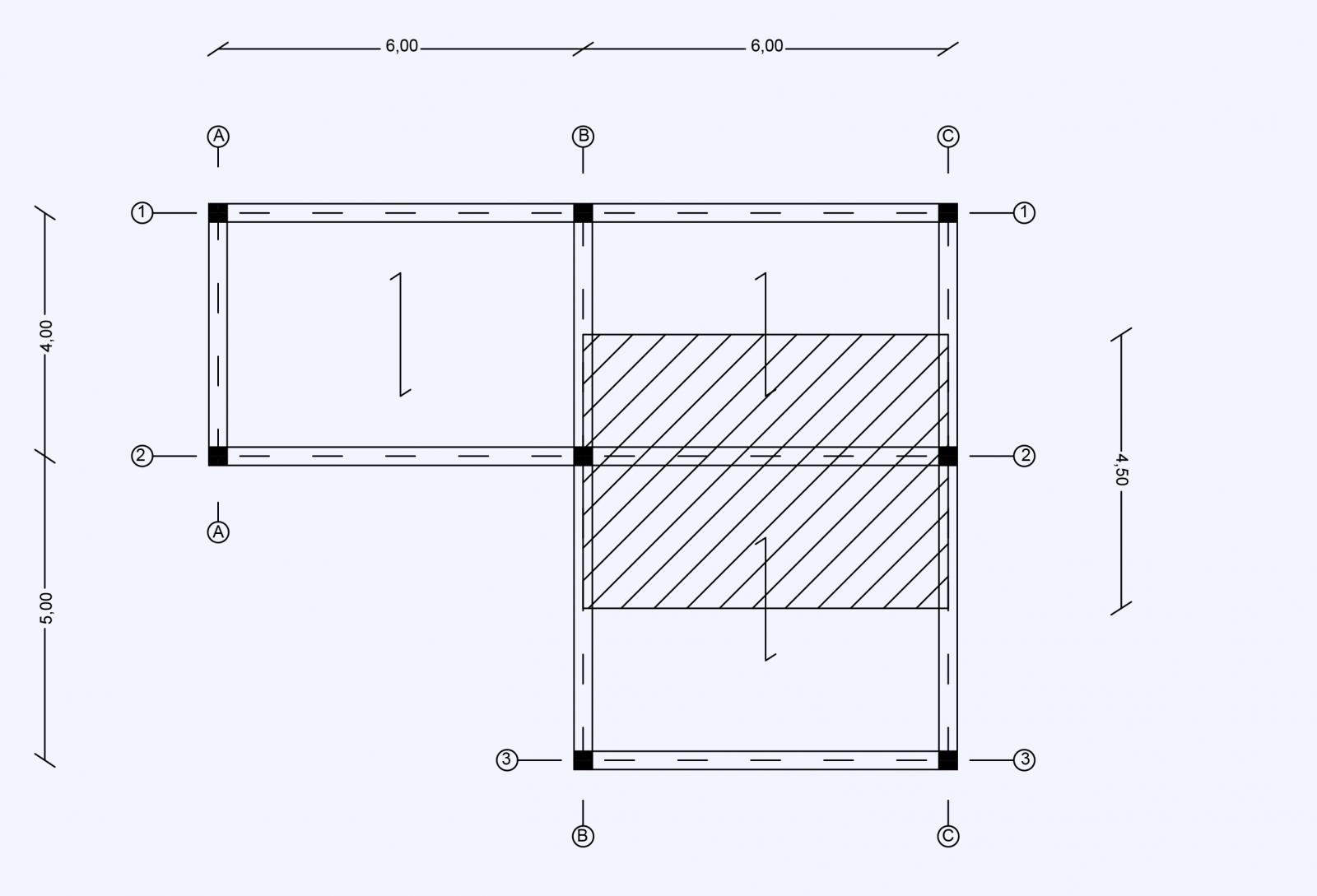
Si distinguono tre diversi tipi di carico:

Qs (KN/mq) CARICO STRUTTURALE  dovuto al peso proprio di tutti gli elementi costruttivi con funzione portante ( peso travetti, pignatte,peso proprio, soletta, rete elettrosaldata )

Qp (KN/mq) = CARICO PERMANENTE non strutturale dato  dunque da tutti gli elementi che non svolgono una funzione portante. ( massetto, pavimento, isolante, controsoffitto ) . A questi si aggiunge il carico dato dai tramezzi pari a 1KN/mq e quello dato dagli impianti 0,5 KN/mq;

Qa (KN/mq) = CARICO ACCIDENTALE viene dato dalla normativa in base allo destinazione d’uso degli ambienti. 

SOLAIO IN ACCIAIO 

CARICO STRUTTURALE

Soletta in cls

Spessore della soletta =   12 cm = 0.12 m

Volume soletta al mq  =   0.12 m x 1,00 m x 1,00 m = 0,12 m³/m²

Sapendo che la densità del cls è di 2100 kg/m³ moltiplicando i due valori ottengo il peso specifico

0,12 m³/m² x 2100 kg/m³ = 252 kg/m²

 (252 x 9,8)/1000 = 2,46 KN/m²

Travetti

Per quanto riguarda i travetti è importante considerare l’interasse. Nel nostro caso i travetti si trovano ad un interasse di 1 metro. Dunque 1/i = 1. In un metro di solaio abbiamo 1 travetto.

Dal sito oppo vado a questo punto a trovare l’ipe presa in considerazione IPE140.

Peso  travetto al m²= 12,9 kg/m x 1,00 m= 12,9 kg/m²=0,126 Kn/m²

Lamiera grecata

HI-BOND TIPO A 55/P 600 TYPE A 55/P600

Avendo la lamiera uno spessore di 0.8 mm vado a vedere il peso specifico inerente a quello spessore

10,47 kg/m² . Trasformo anch’esso in kN/m²

10,47 kg/m² = 0,102 kN/m²

Rete elettrosaldata

820/2  AD

Peso 4,08 kg/m²= 0,039 kN/m²

CARICO STRUTTURALE

Soletta in cls

Spessore della soletta =   12 cm = 0.12 m

Volume soletta al mq  =   0.12 m x 1,00 m x 1,00 m = 0,12 m³/m²

Sapendo che la densità del cls è di 2100 kg/m³ moltiplicando i due valori ottengo il peso specifico

0,12 m³/m² x 2100 kg/m³ = 252 kg/m²

 (252 x 9,8)/1000 = 2,46 KN/m²

Travetti

Per quanto riguarda i travetti è importante considerare l’interasse. Nel nostro caso i travetti si trovano ad un interasse di 1 metro. Dunque 1/i = 1. In un metro di solaio abbiamo 1 travetto.

Dal sito oppo vado a questo punto a trovare l’ipe presa in considerazione IPE140.

Peso  travetto al m²= 12,9 kg/m x 1,00 m= 12,9 kg/m²=0,126 Kn/m²

Lamiera grecata

HI-BOND TIPO A 55/P 600 TYPE A 55/P600

Avendo la lamiera uno spessore di 0.8 mm vado a vedere il peso specifico inerente a quello spessore

10,47 kg/m² . Trasformo anch’esso in kN/m²

10,47 kg/m² = 0,102 kN/m²

Rete elettrosaldata

820/2  AD

Peso 4,08 kg/m²= 0,039 kN/m²

CARICHI STRUTTURALI TOTALI: 2,46 KN/m² + 0,126 Kn/m² + 0,102 kN/m² + 0,039 kN/m² = 2,72 KN/m²

CARICO PERMANENTE

Massetto in cls allegerito

Spessore 5 cm = 0.05 m

Densità γ = 1800 Kg/m³

Volume al m² 0,05 m  x 1,00 m x 1,00 m = 0.05 m³/m²

Peso specifico = 0.05 m³/m² x 1800 Kg/m³  = 90 Kg/m² = 0,882 kN/m²

Controsoffitto

Spessore 1,5 cm = 0.015 m

Densità γ = 1325 Kg/m³

Volume al m² 0,015 m  x 1,00 m x 1,00 m = 0.015 m³/m²

Peso specifico = 0.015 m³/m² x 1325 Kg/m³  = 19,875 Kg/m² = 0,194 kN/m²

Pavimento

Spessore 1,8 cm = 0.018 m

Densità γ = 700 Kg/m³

Volume al m² 0,018 m  x 1,00 m x 1,00 m = 0.018 m³/m²

Peso specifico = 0.018 m³/m² x 700 Kg/m³  = 12,6 Kg/m² = 0,1223 kN/m²

Incidenza Impianti: 0,5 KN/m²

Incidenza Tramezzi: 1 KN/m²

CARICHI PERMANENTI TOTALI: 0,882 kN/m² +  0,194 kN/m² + 0,1223 kN/m² +  0,5 KN/m² + 1 KN/m² = 2,70 KN/m²

CARICO ACCIDENTALE

Infine devo tenere in considerazione anche i  carichi accidentali. Nel mio caso la tipologia è quella degli uffici  dunque

Cat. B2- Uffici aperti al pubblico= 3 kN/m^2​

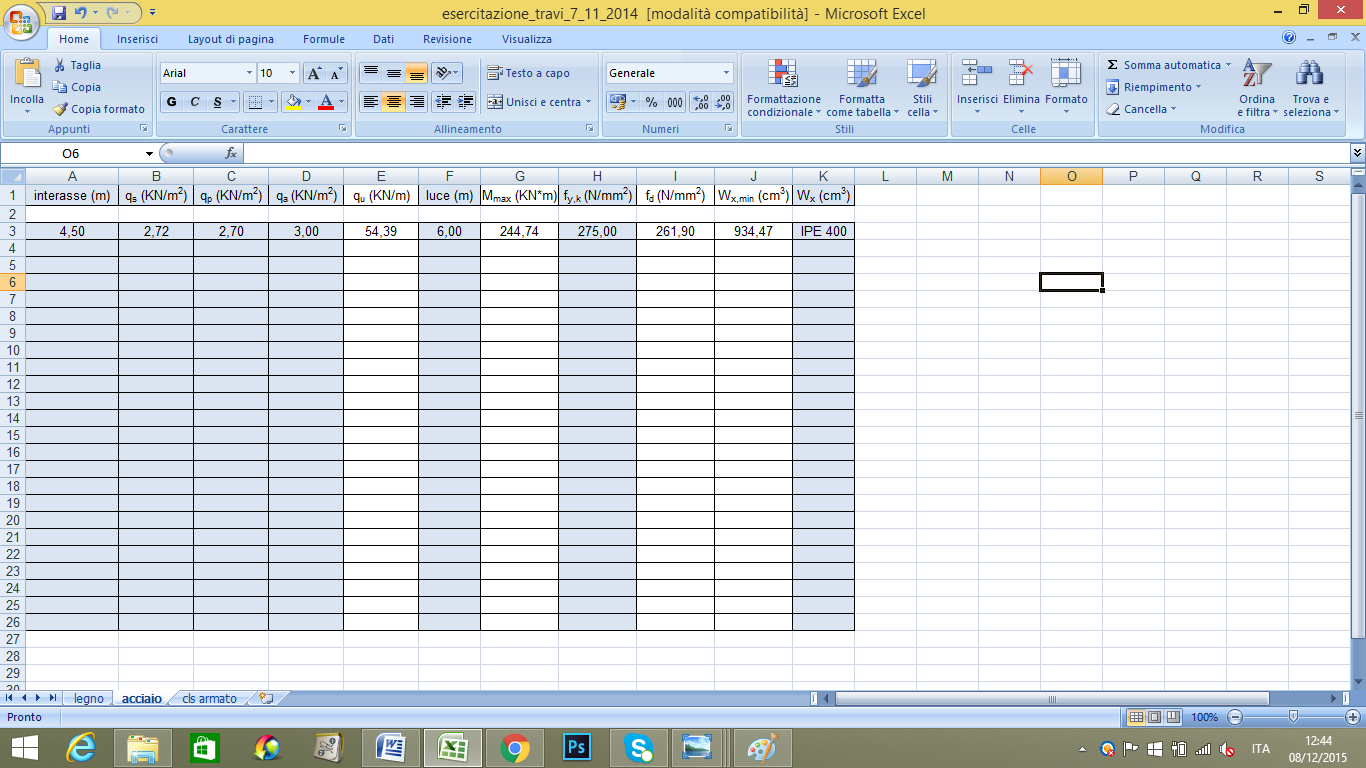
Inserisco tutti i valori trovati nella tabella excel

Trovo il carico ultimo e il momento massimo

Q_u= 1,3 q_s+1,5q_p+1,5q_a

M_max= ql²/8

Scelgo ACCIAIO  Fe 430/S275 con tensione caratteristica di snervamento f_yk=275 MPa e una tensione di progetto f_d= 261,9 MPa. Mi trovo infine W_x,min  e lo confronto con i  valori dei profilati IPE sul sito oppo.

IPE 400

SOLAIO IN CEMENTO ARMATO 

CARICHI STRUTTURALI

Getto in cls

0,04 m³/m² x 2100 kg/m³ = 84 kg/m²

 (84 x 9,8)/1000 = 0,82 KN/m²

Per quanto riguarda i travetti e le pignatte è importante considerare l’interasse. Nel nostro caso l’interasse è di 0,5. Dunque 1/i = 2. In un metro di solaio abbiamo 2 travetti e 2 pignatte

Travetti

Volume al mq=   (0.16 m x 0,10 m x 1,00 m) x 2 = 0,032 m³/m²

0,32 m³/m² x 2100 kg/m³ = 67,2 kg/m²

 (336 x 9,8)/1000 = 0,658 KN/m²

Pignatte

Spessore 16  cm = 0.16 m

Densità γ = 1500 Kg/m³

Volume al m² (0,16 m  x 0,40 m x 1,00 m) x 2 = 0.128 m³/m²

Peso specifico = 0.015 m³/m² x 1500 Kg/m³  = 192 Kg/m² = 1,8 kN/m²

Rete elettrosaldata

815/2  AD

Peso 5,30  kg/m²= 0,052 kN/m²

CARICHI STRUTTURALI TOTALI: 3,33 KN/m²

CARICHI PERMANENTI

Pavimento in cotto

Spessore 2,5 cm = 0.025 m

Densità γ = 40 KN/m³

Volume al m² 0,025 m  x 1,00 m x 1,00 m = 0.025 m³/m²

Peso specifico = 0.025 m³/m² x 40 Kg/m³  = 1 KN/m²

Massetto

 (0,04 x 1,00 x 1,00) m³/m²  x 1800kg/m³ = 72,0 kg/m² = 0,72 kN/m²

Intonaco

Spessore 1,5 cm = 0.015 m

Densità γ = 12 KN/m³

Volume al m² 0,015 m  x 1,00 m x 1,00 m = 0.015 m³/m²

Peso specifico = 0.015 m³/m² x 12 KN/m³ = 0,18 KN/m²

Isolante acustico

Spessore 1,3 cm = 0.013 m

Peso specifico = 0,05 kN/m²

Incidenza Impianti:0,5 KN/m²

Incidenza Tramezzi:1 KN/m²

CARICHI PERMANENTI TOTALI: 3,45 KN/m²

CARICHI ACCIDENTALI  3 kN/m^2​

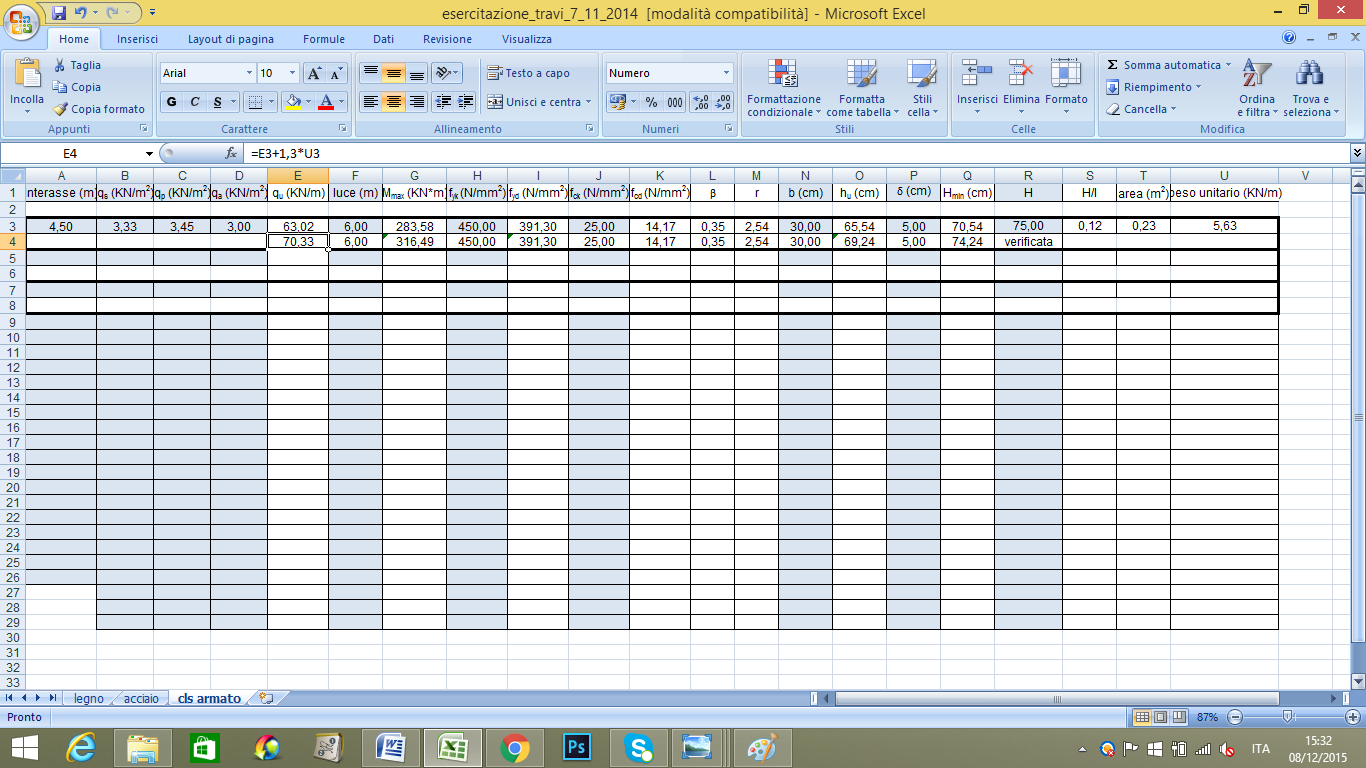
Inserisco tutti i valori trovati nella tabella excel

Trovo il carico ultimo e il momento massimo. Dopo scelgo la classe di resistenza sia per l’armatura in acciaio sia per il calcestruzzo. Inserisco la misura della base e δ=5. Per il cemento armato devo tenere in considerazione anche il peso proprio. 

H=75 cm

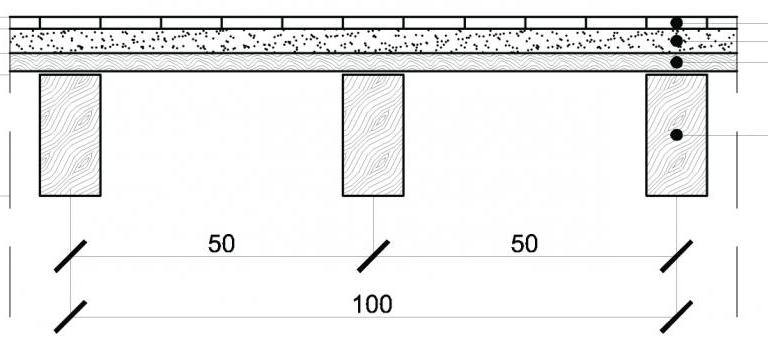
SOLAIO IN LEGNO

CARICO STRUTTURALE

Per quanto riguarda i travetti è importante considerare l’interasse. Nel nostro caso l’interasse è di 0,5. Dunque 1/i = 2. In un metro di solaio abbiamo 2 travetti

Travetti 0,04 m³/m² x 5 kN/m³ = 0,2 kN/m²

TAVOLATO 0.03 m³/m² x 5  KN/m³  = 0,15 kN/m²

CARICHI STRUTTURALI TOTALI: 0,35 KN/m²

CARICO PERMANENTE

Pavimento in legno rovere 0.02 m³/m² x 7 KN/m³  = 0,14 KN/m²

Massetto  (0,04 x 1,00 x 1,00) m³/m²  x 1800kg/m³ = 72,0 kg/m² = 0,72 kN/m²

Incidenza Impianti:0,5 KN/m²

Incidenza Tramezzi: 1 KN/m²

CARICHI PERMANENTI TOTALI: 2,36 KN/m²

  CARICO ACCIDENTALE 3 kN/m² 

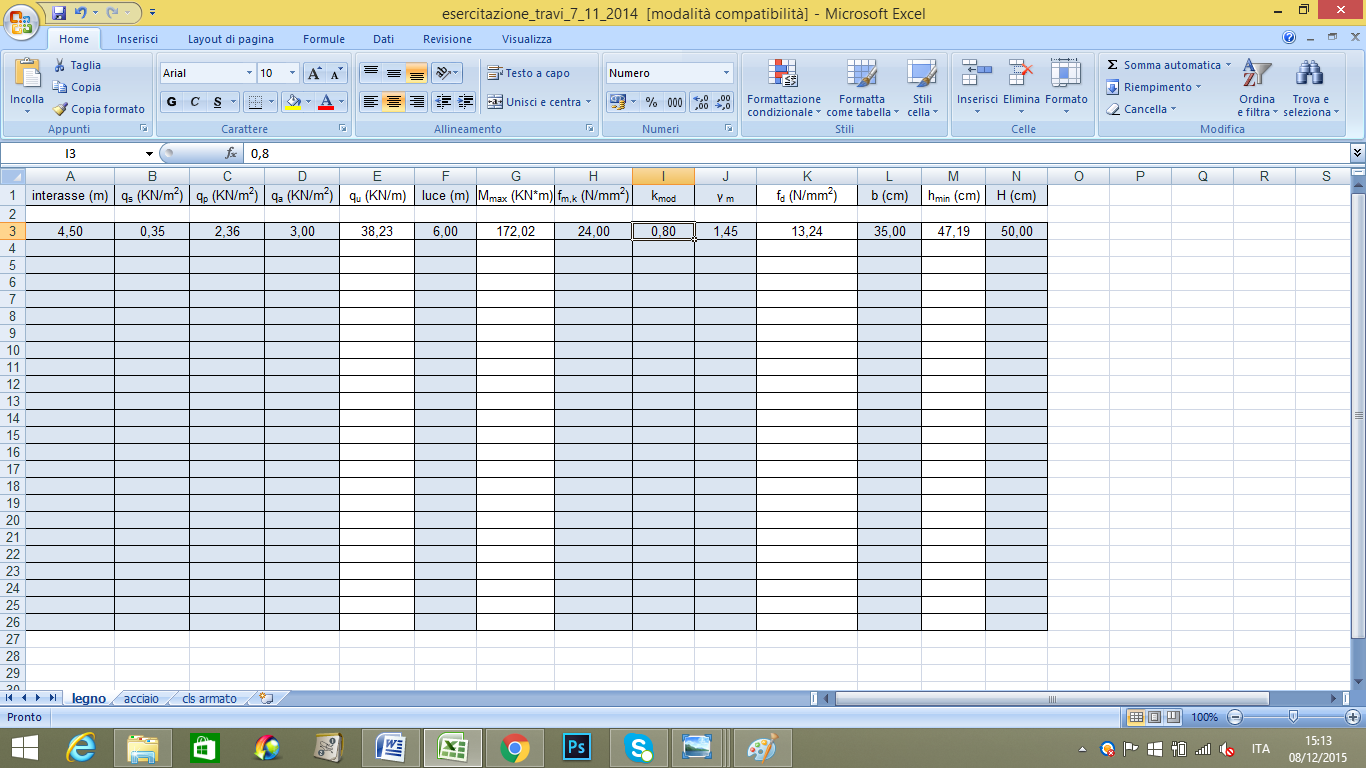
Inserisco tutti i valori trovati nella tabella excel Trovo il carico ultimo e il momento massimo. 

Deciso il tipo di di legno impiegato GL24h,  inserisco i coeff.   k_mode g_m 

k_mod 0,6 dipende dalla di durata del carico(  permanente nel mio caso ) e dalla                classe di servizio ( classe 1 -> È caratterizzata da un’umidità del materiale in equilibrio con l’ambiente a una temperatura di 20°C e un’umidità relativa dell’aria circostante che non superi il 65%, se non per poche settimane all’anno. )

g_m 1,45  

H= 50 cm

In questa terza esercitazione dimensioneremo una mensola verificando che il valore del rapporto tra la luce e l’abbassamento v_max sia maggiore di 250.

La mensola in questione ha luce di 3 m e interasse di 6 m. La sua area di influenza (segnata in verde) è di 18 mq.

Per poter dimensionare la mensola abbiamo bisogno di determinare i carichi gravanti su di essa, che si distinguono in carichi strutturali (qs), carichi permanenti non strutturali (qp) e infine carichi accidentali (qa). Questi carichi sono già stati calcolati per la precedente esercitazione.

Altro dato determinante ai fini del dimensionamento è il valore del momento massimo M_max. Trattandosi di una mensola il momento massimo sarà pari a ql²/2. 

ACCIAIO

TOTALE CARICHI STRUTTURALI qs = q1 + q2  = 2,492 KN/m²

TOTALE CARICHI PERMANENTI qp:  q1 + q2+ q3 + q4 + q5 = 2,9 KN/m²

TOTALE CARICHI ACCIDENTALI qa: Carico secondo normativa: 2 KN/m²

Combinazione allo SLU per 1mq di solaio: q = 2,492 (1,3) + 2,9 (1,5) + 2 (1,5) = 10,6 KN/m²
Carico totale agente sulla trave: qtot = q x A = 10,6 KN/m² x 18 m² = 190,8 KN
Carico lineare agente sulla trave: qu = q x i= 10,6 x 6m = 63,6 KN/m
Momento massimo della trave: Mmax = (qu x l²)/2 = (63,6 x 3²)/2 = 286 KNm

Tensione caratteristica di snervamento (acciaio S275): f_yk =235 MPa
Tensione caratteristica di progetto: f_yd = 223,81 MPa
Modulo di resistenza a flessione (minimo): W_x,min = 1277,5 cm³

DAL SAGOMARIO SCELGO IPE 450 => Wx,min = 1500 cm3  

Inserisco nella tabella Excel il valore del momento di inerzia Ix = 33740 cm4

Posso verificare che la sezione scelta rispetti i limiti di abbassamento, calcolando il Qe con cui è possibile calcolare l’abbassamento massimo della trave vmax e verificare che il rapporto tra luce e abbassamento sia maggiore di 250 (come da normativa). 

CALCESTRUZZO ARMATO

TOTALE CARICHI STRUTTURALI qs = q1 + q2 + q3 = 3,42 KN/m²

TOTALE CARICHI PERMANENTI qp:  q1 + q2+ q3 + q4 + q5 + q6 + q7 = 4,38 KN/m²

TOTALE CARICHI ACCIDENTALI qa: Carico secondo normativa: 2 KN/m²

Combinazione allo SLU per 1mq di solaio: q = 3,42 (1,3) + 4,38 (1,5) + 2 (1,5) = 14 KN/m²
Carico totale agente sulla trave: qtot = q x A = 14 KN/m² x 18 m² = 252 KN
Carico lineare agente sulla trave: qu = q x i= 14 x 6m = 84 KN/m
Momento massimo della trave: Mmax = (qu x l²)/2 = (84 x 3²)/2 = 378 KNm

Resistenza caratteristica dell’acciaio: f_yk= 450 MPa  
Resistenza caratteristica del cls: f_ck = 30 Mpa
Resistenza di progetto dell’acciaio: f_yd = f_yk / 1,15 = 391,30 Mpa
Resistenza di progetto del cls: f_cd = 0,83 x (f_ck/ 1,15) = 17 Mpa

Valore della base della trave (ipotizzato): b = 40 cm
Altezza utile della trave: hu = r (Mmax x 100 / f_cd x b))0,5 = 56,99 cm
Altezza minima della trave: hmin = hu + δ = 61,99 cm  dove δ è uguale alla distanza tra il baricentro dell’armatura ed il filo del cls teso
Valore di H scelto: H = 65 cm

A questo punto posso ottenere il peso unitario della trave e il Qe e verifico che:
l/v_max > 250
In questo caso è pari a 960 quindi la sezione è verificata

LEGNO

TOTALE CARICHI STRUTTURALI qs = q1 + q2 = 0,84 KN/m²

TOTALE CARICHI PERMANENTI qp:  q1 + q2+ q3 = 2 KN/m2

TOTALE CARICHI ACCIDENTALI qa: Carico secondo normativa: 2 KN/m2

Combinazione allo SLU per 1mq di solaio: q = 0,84 (1,3) + 2 (1,5) + 2 (1,5) = 7,092 KN/m²
Carico totale agente sulla trave: qtot = q x A = 7,092 KN/m² x 18 m² = 127,65 KN
Carico lineare agente sulla trave: qu = q x i= 7,092 x 6m = 42,55 KN/m
Momento massimo della trave: Mmax = (qu x l²)/2 = (42,55 x 3²)/2 = 191,5 KNm

Resistenza a flessione caratteristica: f_m,k = 24 MPa (dipende dal tipo di legno) 
Coefficiente di durata del carico: k_mod= 0,6 
Coefficiente parziale di sicurezza del materiale: γm= 1,50 
Tensione ammissibile: f_d = f_m,k x k_mod / γm = 9,60 MPa

Valore della base della trave (ipotizzato): b = 35 cm
Altezza minima della trave: hmin = (interasse x Mmax x 1000 / (b x f_d)^0,5 = 54,70  cm
Valore di H scelto: H = 60 cm
 

Devo calcolare l’abbassamento della trave v_max, in quanto il rapporto tra luce ed abbassamento deve essere, per normativa, maggiore di 250

l/v_max > 250

In questo caso è di 740,24 quindi la sezione è verificata

Come nella precedente esercitazione, per dimensionare la trave, bisogna calcolare i carichi che agiscono su di essa (Qu= (qs x γ_G1 + qp x γ_G2  + qa x γ_G3  x interasse) e il momento massimo. La trave in questo caso non è più appoggiata ma si comporta come una mensola. Quindi il momento massimo non è più Mmax= (qu x l^2)/8 ma --> Mmax=(qu x l^2)/2

CARICHI STRUTTURALI

- Tavolato in legno           -->   γ = 6,00 KN/mc

                                                    S = 2,5 cm   0,025 m

                                                    P.P = 6 x 0,025 = 0,15 KN/mq

- Travetti i= 1 m L=6 m    -->   γ = 6,00 KN/mc

                                                    Volume = ( 0,08 m x 0,10 m x 1m ) 3m = 0,024 mc

                                                    P.P = 6 x 0,024 = 0,144 KN/mq

TOTALE CARICHI STRUTTURALI = 0,294 KN/mq

CARICHI PERMANENTI

- Pavimento (2 cm)         -->   P.P 0,40 KN/mq

- Massetto il cls               -->   γ = 20,00 KN/mc

                                                  S = 11 cm   0,11 m

                                                  P.P = 20 x 0,11 = 2,2 KN/mq

TOTALE CARICHI PERMANENTI = 2,6 KN/mq

CARICHI ACCIDENTALI

Cat. A _ Civile abitazione à 2 KN/mq

PROGETTO

Combinazione di carico allo SLU per 1 mq di solaio --> q =0,294 x 1,3+2,6x 1,5+2 x 1,5 =  7,28 KN/mq

Carico del solaio portato della trave --> qtot = q x A = q x i x l = 7,28 KN/mq x 24 mq = 174,72 KN

Carico lineare agente sulla trave --> qu = qtot / l = q x i = 7,28 KN/mq x 6 m = 43,68 KN/m

Momento massimo della trave --> Mmax = (qu x l^2)/2 = (43,68 x 16)/2= 349,44  KNm

Tensione di progetto --> fd = kmod x fm,k / γm = 0,8 x 24 [N/mmq] / 1,45 = 13,24 N/mmq

Infine, ipotizzo il valore della base b (40 cm) e calcolo l’altezza minima hmin che deve avere la trave:

hmin = (interasse x Mmax x 1000 / b x fd)0,5 = 73,90 cm Valore di H scelto : 75 cm

VERIFICA

Per la mensola è necessario calcolare e verificare l’abbassamento della trave. Determino quindi il modulo elastico  (E=8000) e il momento d'inerzia (Ix=(b*h^3) /12) e carico totale qe (combinazione di carico frequente per SLE reversibili), necessario per il calcolo dello spostamento.

Qe = (G1 + G2 + Ψ1 x  Q1) x i

Calcolo cosi l'abbassamento max (Vmax) e verificare che il rapporto tra la luce della trave e il suo spostamento max sia maggiore di 250, come da normativa.

Vmax=qel^4/8EIx                                 l/ Vmax ≥ 250

CARICHI STRUTTURALI

- Soletta in cls                            -->   γ = 25,00 KN/mc

                                                     S = 4 cm   0,04 m

                                                     P.P = 25 x 0,04 = 1 KN/mq

- Travetti                                     -->   γ = 25,00 KN/mc

                                                     Smedio = 0,12 x 0,2 / 0,50 = 0,048 m

                                                     P.P =  25 x 0,048 = 1,20 KN/mq

- Pignatte                                    -->   γ = 8,00 KN/mc

                                                     Smedio = 0,38 x 0,2 / 0,50 = 0,152 m         

                                                     P.P. =  8 x 0,152 = 1,22 KN/mq   

TOTALE CARICHI STRUTTURALI = 3,42 KN/mq  

CARICHI PERMANENTI

- Pavimento (s = 20 mm)         --> P.P. = 0,40 KN/mq

- Massetto di allettamento     --> γ = 20,00 KN/mc

  in cls alleggerito                            S = 80 mm = 0,08 m

                                                           P.P = 20 x 0,08 = 1,6 KN/mq

-Isolante acustico (s = 40 mm)   -->  P.P. = 0,40 KN/mq

-Isolante acustico (s = 40 mm)   -->  P.P. = 0,40 KN/mq

-Massetto in malta di cemento  -->   γ = 25,00 KN/mc

                                                                     S = 40 mm = 0,04 m

                                                                     P.P. =  25 x 0,04 = 1 KN/mq

-Intonaco                                          -->   γ=18,00 KN/mc

                                                                     S= 20 mm = 0,02 m

                                                                     P.P. =18 x 0,02 = 0,36 KN/mq

Incidenza impianti                         --> 0,5 KN/mq

Incidenza tramezzi                         --> 1,60 KN/mq

TOTALE CARICHI PERMANENTI = 5,76 KN/mq         

CARICHI ACCIDENTALI  

Cat. A _ Civile abitazione à 2 KN/mq 

PROGETTO          

Combinazione di carico allo SLU per 1 mq di solaio -->  q =3,42 x 1,3 + 5,76 x 1,5 + 2 x 1,5 = 16,09 KN/mq

Carico del solaio portato della trave --> qtot = q x A = q x i x l = 16,09 KN/mq x 24 mq = 386,16 KN

Carico lineare agente sulla trave --> qu = qtot / l = q x i = 16,09 KN/mq x 6 m = 96,54 KN/m

Momento massimo della trave --> Mmax = (qu x l^2)/2 = (96,54 x 16)/2 = 772,32 KN*m

Stabilendo fyk ( 450  N/mmq ) e fck ( 45  N/mmq ) si ottengono:

tensione di progetto dell’acciaio -->  fyd = fyk/1,15 = 391,30 N/mmq 

tensione di progetto del cls compresso --> fcd = αcc x (fck / γc) = 0,85 x (45/1,5) = 25,5 N/mmq.

Infine, ipotizzo il valore della base b (40 cm) e calcolo l’altezza minima hmin che deve avere la trave:

hu= r • (Mmax • 1000 / (fcd• b))0,5   = 60,56 cm  

Hmin= hu + δ = 65,56 cm

(con δ= copriferro= 5 cm)

Infine assegno una altezza H (70 cm) maggiore di Hmin per tenere conto del peso proprio della trave.

VERIFICA

 Verifica ad abbassamento dove Vmax=qel^4/8EIx e l/ Vmax ≥ 250

CARICHI STRUTTURALI

-Lamiera grecata tipo HI BOND A55/P600         --> S = 0,07 m

                                                                                   --> P.P=0,092 KN/mq

Gettata di cls alleggerito                                       --> γ = 20,00 KN/mc

                                                                                  -->  Stot = 0,12 m

                                                                                  --> P.P = 2,4 KN/mq

TOTALE CARICHI STRUTTURALI  = 2,492 KN/m2

CARICHI PERMANENTI

- Pavimento                                                            -->  γ = 20,00 KN/mc

                                                                                 -->  S= 0,02 m

                                                                                 --> P.P= 20 x 0,02 = 0,4 KN/mq

 - Massetto in cls                                                   -->  γ = 20,00 KN/mc

                                                                                 --> S= 0,035 m

                                                                                 --> P.P = 20 x 0,035 = 0,7 KN/mq

- Isolante acustico Fonoroll pb                           --> γ = 10 KN/mc

                                                                                 --> S = 0,03 m

                                                                                 --> P.P = 0,3 KN/mq

- Incidenza impianti                                              --> 0,5 KN/mq

- Incidenza tramezzi                                              -->1 KN/mq

TOTALE CARICHI PERMANENTI = 2,9 KN/m2

CARICHI ACCIDENTALI

Cat. A _ Civile abitazione à 2 KN/mq 

PROGETTO

Combinazione allo SLU per 1mq di solaio -->  q = 2,492 (1,3) + 2,9 (1,5) + 2 (1,5) = 10,6 KN/m2

Carico totale agente sulla trave --> qtot = q x A = 10,6 KN/m2 x 24 mq = 254,4 KN

Carico lineare agente sulla trave --> qu = q x i= 10,6 x 6m = 63,6 KN/m

Momento massimo della trave --> Mmax = (qu x l^2)/2 = (63,6 x 16)/2 = 508,8 KNm

Tensione caratteristica di snervamento (acciaio S275) --> fyk =275 MPa

Tensione caratteristica di progetto --> fyd = 261,90 MPa

Modulo di resistenza a flessione (minimo) --> Wx,min = 1940 cmq

DAL SAGOMARIO SCELGO IPE 500 => Wx,min = 2194  cm3 

VERIFICA

Inserisco quindi nella tabella Excel il momento di inerzia (Ix = 48200 cm^4) e il peso (0,907 Kn/m) e il modulo di elasticità (E = 210000). Con questi ultimi dati posso verificare se la sezione scelta rispetta i limiti di abbassamento. Il foglio infatti mi calcolerà il Qe, con cui sarà possibile calcolare l'abbassamento max (Vmax) e verificare che il rapporto tra la luce della trave e il suo spostamento max sia maggiore di 250, come da normativa.

Ipotizzando l’uso di tre diversi materiali (legno, acciaio e calcestruzzo) l’esercitazione consiste nel dimensionare la trave maggiormente sollecitata all’interno della propria pianta di carpenteria. La trave maggiormente sollecitata è quella soggetta ad una maggiore area d’influenza evidenziata in rosso di 5m (interasse) x6m (luce della trave) =30 mq .

CARICHI STRUTTURALI

- Tavolato in legno           -->   γ = 6,00 KN/mc

                                                    S = 2,5 cm   0,025 m

                                                    P.P = 6 x 0,025 = 0,15 KN/mq

- Travetti i= 1 m L=6 m    -->   γ = 6,00 KN/mc

                                                    Volume = ( 0,08 m x 0,10 m x 1m ) 3m = 0,024 mc

                                                    P.P = 6 x 0,024 = 0,144 KN/mq

TOTALE CARICHI STRUTTURALI = 0,294 KN/mq

CARICHI PERMANENTI

- Pavimento (2 cm)         -->   P.P 0,40 KN/mq

- Massetto il cls               -->   γ = 20,00 KN/mc

                                                  S = 11 cm   0,11 m

                                                  P.P = 20 x 0,11 = 2,2 KN/mq

TOTALE CARICHI PERMANENTI = 2,6 KN/mq

CARICHI ACCIDENTALI

Cat. A _ Civile abitazione à 2 KN/mq

PROGETTO

Combinazione di carico allo SLU per 1 mq di solaio --> q =0,294 x 1,3+2,6x 1,5+2 x 1,5 =  7,28 KN/mq

Carico del solaio portato della trave --> qtot = q x A = q x i x l = 7,28 KN/mq x 30 mq = 218,4 KN

Carico lineare agente sulla trave --> qu = qtot / l = q x i = 7,28 KN/mq x 5 m = 36,4KN/m

Momento massimo della trave --> Mmax = (qu x l^2)/8 = (36,4 x 36)/8= 163,8 KNm

Tensione di progetto --> fd = kmod x fm,k / γm = 0,8 x 24 [N/mmq] / 1,45 = 13,24 N/mmq

Infine, ipotizzo il valore della base b (40 cm) e calcolo l’altezza minima hmin che deve avere la trave:

 hmin = (interasse x Mmax x 1000 / b x fd)0,5 = 43,08 cmValore di H scelto : 50 cm

CARICHI STRUTTURALI

- Soletta in cls                            -->   γ = 25,00 KN/mc

                                                     S = 4 cm   0,04 m

                                                     P.P = 25 x 0,04 = 1 KN/mq

- Travetti                                     -->   γ = 25,00 KN/mc

                                                     Smedio = 0,12 x 0,2 / 0,50 = 0,048 m

                                                     P.P =  25 x 0,048 = 1,20 KN/mq

- Pignatte                                    -->   γ = 8,00 KN/mc

                                                     Smedio = 0,38 x 0,2 / 0,50 = 0,152 m         

                                                     P.P. =  8 x 0,152 = 1,22 KN/mq   

TOTALE CARICHI STRUTTURALI = 3,42 KN/mq  

CARICHI PERMANENTI

- Pavimento (s = 20 mm)         --> P.P. = 0,40 KN/mq

- Massetto di allettamento     --> γ = 20,00 KN/mc

  in cls alleggerito                            S = 80 mm = 0,08 m

                                                           P.P = 20 x 0,08 = 1,6 KN/mq

-Isolante acustico (s = 40 mm)   -->  P.P. = 0,40 KN/mq

-Isolante acustico (s = 40 mm)   -->  P.P. = 0,40 KN/mq

-Massetto in malta di cemento  -->   γ = 25,00 KN/mc

                                                                     S = 40 mm = 0,04 m

                                                                     P.P. =  25 x 0,04 = 1 KN/mq

-Intonaco                                          -->   γ=18,00 KN/mc

                                                                     S= 20 mm = 0,02 m

                                                                     P.P. =18 x 0,02 = 0,36 KN/mq

Incidenza impianti                         --> 0,5 KN/mq

Incidenza tramezzi                         --> 1,60 KN/mq

TOTALE CARICHI PERMANENTI = 5,76 KN/mq         

CARICHI ACCIDENTALI  

Cat. A _ Civile abitazione à 2 KN/mq 

PROGETTO          

Combinazione di carico allo SLU per 1 mq di solaio -->  q =3,42 x 1,3 + 5,76 x 1,5 + 2 x 1,5 = 16,09 KN/mq

Carico del solaio portato della trave --> qtot = q x A = q x i x l = 16,09 KN/mq x 30 mq = 482,7 KN

Carico lineare agente sulla trave --> qu = qtot / l = q x i = 16,09 KN/mq x 5 m = 80,45 KN/m

Momento massimo della trave --> Mmax = (qu x l^2)/8 = (80,45 x 36)/8 = 362,02 KN*m

Stabilendo fyk ( 450  N/mmq ) e fck ( 45  N/mmq ) si ottengono:

tensione di progetto dell’acciaio -->  fyd = fyk/1,15 = 391,30 N/mmq 

tensione di progetto del cls compresso --> fcd = αcc x (fck / γc) = 0,85 x (45/1,5) = 25,5 N/mmq.

Infine, ipotizzo il valore della base b (40 cm) e calcolo l’altezza minima hmin che deve avere la trave:

hu= r • (Mmax • 1000 / (fcd• b))0,5   = 41,46 cm  

Hmin= hu + δ = 46,46 cm

(con δ= copriferro= 5 cm)

Infine assegno una altezza H (55 cm) maggiore di Hmin per tenere conto del peso proprio della trave.

CARICHI STRUTTURALI

-Lamiera grecata tipo HI BOND A55/P600         --> S = 0,07 m

                                                                                   --> P.P=0,092 KN/mq

Gettata di cls alleggerito                                       --> γ = 20,00 KN/mc

                                                                                  -->  Stot = 0,12 m

                                                                                  --> P.P = 2,4 KN/mq

TOTALE CARICHI STRUTTURALI  = 2,492 KN/m2

CARICHI PERMANENTI

- Pavimento                                                            -->  γ = 20,00 KN/mc

                                                                                 -->  S= 0,02 m

                                                                                 --> P.P= 20 x 0,02 = 0,4 KN/mq

 - Massetto in cls                                                   -->  γ = 20,00 KN/mc

                                                                                 --> S= 0,035 m

                                                                                 --> P.P = 20 x 0,035 = 0,7 KN/mq

- Isolante acustico Fonoroll pb                           --> γ = 10 KN/mc

                                                                                 --> S = 0,03 m

                                                                                 --> P.P = 0,3 KN/mq

- Incidenza impianti                                              --> 0,5 KN/mq

- Incidenza tramezzi                                              -->1 KN/mq

TOTALE CARICHI PERMANENTI = 2,9 KN/m2

CARICHI ACCIDENTALI

Cat. A _ Civile abitazione à 2 KN/mq 

PROGETTO

Combinazione allo SLU per 1mq di solaio -->  q = 2,492 (1,3) + 2,9 (1,5) + 2 (1,5) = 10,6 KN/m2

Carico totale agente sulla trave --> qtot = q x A = 10,6 KN/m2 x 30 mq = 318 KN

Carico lineare agente sulla trave --> qu = q x i= 10,6 x 5m = 53 KN/m

Momento massimo della trave --> Mmax = (qu x l^2)/8 = (42,4 x 30)/8 = 159 KNm

Tensione caratteristica di snervamento (acciaio S275) --> fyk =275 MPa

Tensione caratteristica di progetto --> fyd = 261,90 MPa

Modulo di resistenza a flessione (minimo) --> Wx,min = 607,09 cmq

DAL SAGOMARIO SCELGO IPE 330 => Wx,min = 713 cm3 

Per la verifica si aggiunge il peso proprio della sezione ai carichi strutturali, si ricalcola Mmax e si ridetermina Wx,min che dovrà essere minore di 713 cmq

p.p. IPE = 0,49 KN/m

q = 2,982 (1,3) + 2,9 (1,5) + 2 (1,5) = 11,22 KN/mq

qtot = q x A = 11,22 KN/m2 x 30 mq = 336 KN

qu = q x i= 11,22 x 5m = 56,1 KN/m

Mmax = (qu x l^2)/8 = (56,1 x36 )/8 = 252 KNm

Wx,min = 607,09 cmq      VERIFICATO

L’esercitaione prevede l’analisi della trave più sollecitata di un impalcato strutturale a telaio (travi e pilastri), nella tre diverse teconologie: C.A., ACCIAIO E LEGNO.

Nella figura è rappresentato un impalcato strutturale:

Procedo con l’analisi dei carichi qs, qp , qa per ciascuna tecnologia:                                                                             1) Dimensionamento di una trave in legno.

1.Sovraccarico strutturale qs

-travetto in legno: 2x (0,25*0,4)mq x 6KN/mc= 1,2 KN/mq

-tavolato: (0,03+*1*1)mq  x 6KN/mc = 0,18 KN/mq

Tot.  qs 1,38 KN/mq

2.Sovraccarico permanente qp

-piastrelle in ceramica: 0,01 x 0,2kN/mq = 0,002 KN/mq

-malta di allettamento: 0,02 x 20KN/mq = 0,4 KN/mq

-isolante: 0,04 x 1KN/mq = 0,04 KN/mq

-massetto: 0,08 x 18KN/mq = 1,44 KN/mq

 -Incidenza tramezzi 1 KN/mq  

 -incidenza impianti 0,5 KN/mq

 Tot. qp 3,382 KN/mq

3.Sovraccarico accidentale

   Da normativa per edifici a uso residenziale 2 KN/mq

4.Ora andiamo ad inserire i dati nella tabella excel  inserendo i qs, qp , qa e mi trovo il qu.                                     Inserisco la il valore della luce della trave per trovare quanto vale il Mmax.               

5.Ho scelto il legno lamellare. Inserisco la tensione caratteristica a flessione fmk del legno che equivale a 24 MPa. La normativa mi fornisce la tensione di progetto fmd attraverso il coefficiente diminutivo dei valori di resistenza del materiale kmod = 0,80  ed il coefficiente parziale di sicurezza γm = 1,45 in base al materiale da me scelto. Trovo il valore della tensione di progetto fd.

6.Fisso la base b della trave per trovare hmin della sezione. Trovo il valore di H che deve essere maggiore di hmin.

2) Dimensionamento di una trave in acciaio.

1.Sovraccarico strutturale qs

-lamiera grecata: 0,08 x 0,1 KN/mq = 0,008 KN/mq

-soletta: 0,18 x 25 KN/mq = 4,5 KN/mq

 -peso travetto IPE 140: 0,129 KN/mq

 Tot.  qs 4,637 KN/mq

2.Sovraccarico permanente qp

-piastrelle in ceramica: 0,01 x 0,2kN/mq = 0,002 KN/mq

-malta di allettamento: 0,02 x 20KN/mq = 0,4 KN/mq

-isolante: 0,04 x 1KN/mq = 0,04 KN/mq

-massetto: 0,08 x 18KN/mq = 1,44 KN/mq

 -Incidenza tramezzi 1 KN/mq  

 -incidenza impianti 0,5 KN/mq

 Tot. qp 3,382 KN/mq

3.Sovraccarico accidentale

  Da normativa per edifici a uso residenziale 2 KN/mq

4.Ora andiamo ad inserire i dati nella tabella excel  inserendo i qs, qp , qa e mi trovo il qu.                                     Inserisco la il valore della luce della trave per trovare quanto vale il Mmax.

5.Scelgo la classe dell’acciaio strutturale S275 con tensione caratteristica di snervamento fyk = 275 MPa. Cosi ho trovato la tensione di progetto fd, in questo modo ricavo il modulo di resistenza minimo rispetto all'asse x Wx,min = 841,08. Scelgo la sezione della trave IPE ( IPE 360) consultando la tabella dei Profilati metallici sul sito www.oppo.it e scegliendo un profilato con Wx > Wx,min.

3)Dimensionamento di una trave in  calcestruzzo armato.

1.Sovraccarico strutturale qs

-pignatte:  2 x 8 kg = 16 kg = 0,16 KN

-travetti: (0,16 *0,1*1) x 25 KN/mc = 0,4 KN

 -soletta: 0,04 m x 25 KN/mc = 1 KN/mc

 Tot.  qs 1,56 KN/mc

2.Sovraccarico permanente qp

-piastrelle in ceramica: 0,01 x 0,2kN/mq = 0,002 KN/mq

-malta di allettamento: 0,02 x 20KN/mq = 0,4 KN/mq

-isolante: 0,04 x 1KN/mq = 0,04 KN/mq

-massetto: 0,08 x 18KN/mq = 1,44 KN/mq

 -Incidenza tramezzi 1 KN/mq  

 -incidenza impianti 0,5 KN/mq

 Tot. qp 3,382 KN/mq

3.Sovraccarico accidentale

   Da normativa per edifici  a uso residenziale 2 KN/mq

4.Ora andiamo ad inserire i dati nella tabella excel  inserendo i qs, qp , qa e mi trovo il qu.                                     Inserisco la il valore della luce della trave per trovare quanto vale il Mmax.

5.Uso la classe di resistenza caratteristica dell'acciaio fyk da armatura B450C che vale 450 MPa (N/mm²) e la classe di resistenza del calcestruzzo fck per uso ordinario C2530 che equivale a 25 MPa. Excel calcola la tensione di progetto dell'acciaio fyd, servendosi del coefficiente riduttivo per le resistenze a lunga durata acc = 0,85, e la tensione di progetto del calcestruzzo (fcd) servendosi del coefficiente parziale di sicurezza del calcestruzzo γc = 1,15.

6.Inserisco la base b della trave (35 cm) così da trovare l'altezza utile della sezione hu dalla quale ricaverò l'altezza minima della sezione Hmin. Per verificare la correttezza della trave Hmin < H.

L'obiettivo della terza esercitazione è quello di dimensionare una trave a sbalzo, in legno, acciaio e cemento armato, in modo tale che il suo abbassamento massimo sia minore di 1/250 della luce come da normativa.

Consideriamo un solaio 10m*10m con uno sbalzo di 3m.

Individuando le aree di influenza deduco che la trave più sollecitata è la 4-7 e che, considerando solo la luce dell'aggetto, presenta una luce di 3,00m. A questo punto calcolo i carichi che gravano sul solaio, per tutte e tre le tipologie: LEGNO, ACCIAIO E CEMENTO ARMATO.

SOLAIO IN LEGNO

Carichi strutturali (qs): 0,7 KN/mq

                                    Trave + Travetti + Regolo

Carichi permanenti (qp): 1,76 KN/mq

                                      Pavimento + Malta d'allettamento + Massetto + Tavolato + Controsoffitto

Carichi accidentali (qa): 2 KN/mq

                                       Sovraccarico d'esercizio per edificio residenziale da normativa

Ora inserisco i dati nel foglio Excell e controllo che l'abbassamento massimo rispetti i limiti del 1/250 della luce e per fare questo bisogna verificare la trave allo STATO LIMITE D'ESERCIZIO (qe), ovvero il limite di carico oltre il quale la trave perde la sua funzionalità strutturale e la sua efficienza. Per trovare l'abbassamento avrò inolte bisogno del Modulo di Young E (per il legno 8000 N/mmq e il momento di inerzia che verrà calcolato in automatico.

Lo spostamento massimo sarà cosi uguale a 1,00 cm e risulta minore di 300/250 quindi la trave è verificata a deformabilità.

SOLAIO IN ACCIAIO

Carichi strutturali (qs): 1,7 KN/mq

                                    Travetto IPE + Lamiera grecata + Getto di CLS

Carichi permanenti (qp): 0,778 KN/mq

                                      Pavimento + Malta d'allettamento + Isolante + Controsoffitto

Carichi accidentali (qa): 2 KN/mq

                                       Sovraccarico d'esercizio per edificio residenziale da normativa

Ora inserisco i dati nel foglio Excell scegliendo il profilato principale IPE 300 e controllo che l'abbassamento massimo rispetti i limiti del 1/250 della luce e per fare questo bisogna verificare la trave allo STATO LIMITE D'ESERCIZIO (qe), ovvero il limite di carico oltre il quale la trave perde la sua funzionalità strutturale e la sua efficienza. Per trovare l'abbassamento avrò inolte bisogno del Modulo di Young E (per l'acciaio 21000 N/mmq e il momento di inerzia l'ho inserito quando ho scelto il tipo di profilo.

Lo spostamento massimo sarà cosi uguale a 1,014 cm e risulta minore di 300/250 cm quindi la trave è verificata a deformabilità.

SOLAIO IN CEMENTO ARMATO 

Carichi strutturali (qs): 3,05 KN/mq

                                    Calcestruzzo + Pignatta

Carichi permanenti (qp): 1,478 KN/mq

                                      Pavimento + Malta d'allettamento + Isolante + Massetto + Intonaco

Carichi accidentali (qa): 2 KN/mq

                                       Sovraccarico d'esercizio per edificio residenziale da normativa

Ora inserisco i dati nel foglio Excell e controllo che l'abbassamento massimo rispetti i limiti del 1/250 della luce e per fare questo bisogna verificare la trave allo STATO LIMITE D'ESERCIZIO (qe), ovvero il limite di carico oltre il quale la trave perde la sua funzionalità strutturale e la sua efficienza. Per trovare l'abbassamento avrò inolte bisogno del Modulo di Young E (per il cemento armato 21000 N/mmq e il momento di inerzia calcolato automaticamente.

Lo spostamento massimo sarà cosi uguale a 0,47 cm e risulta minore di 300/250 cm quindi la trave è verificata a deformabilità.