Esercitazione

1_Analisi azioni del vento

Al fine di completare la consegna precedente, è stata svolta l'analisi delle azioni del vento. Per questo passaggio, sono stati assegnati dei carichi distribuiti sui pilastri sia lungo un lato corto sia su un lato lungo dell'edificio, quindi lungo 2 direzioni e versi se osservato sul piano orizzontale.

E' stato calcolato l'interasse dell'area di influenza in facciata di ogni pilastro, espresso in m, e poi è stato moltiplicato per il carico dell'azione del vento di valore pari a 0,5 KN/m². Successivamente sono stati assegnati i carichi distribuiti sul modello di SAP2000 ed è stata eseguita l'analisi, per trovare le tensioni agenti sui pilastri e verificarli a pressoflessione, tenendo conto del carico del vento combinato con il carici verticali. La tensione massima alla quale il pilastro è sollecitato è fornita dalla sovrapposizione degli effetti dello sforzo normale e del momento flettente trasmesso dalla trave.

Verifica a pressoflessione del pilastro: N/A + M_max/W_max < fcd

Con fcd = resistenza di progetto del calcestruzzo

 

Diagramma del momento flettente

Diagramma dello sforzo normale

Deformata

Analisi dell'abbassamento

I pilastri da verificare a pressoflessione sul file Excel sono un pilastro tipo in facciata sul lato corto dell'edificio ed un pilastro tipo all'angolo.

Dal risultato si evince che il progetto dei pilastri è verificato.

 

 

 

 

 

 

 

La terza esercitazione consiste nel calcolare come il telai che costituiscono la struttura dell'edificio della precedente esercitazione si ripartiscono la  forza sismica, applicando il metodo delle rigidezze.

Il telaio preso in considerazione è il seguente:

I telai che compongono la struttura sono:
1_O, costituito dai pilastri: 1-2-3
2_O, costituito dai pilastri: 4-5-6
3_O, costituito dai pilastri: 7-8-9
4_O, costituito dai pilastri: 10-11-12
1_V, costituito dai pilastri: 1-4-7-10-13
2_V, costituito dai pilastri: 2-5-8-11-14
3_V, costituito dai pilastri: 3-6-9-12-15

Successivamente, si determina la rigidezza dei telai prendendo in considerazione ogni singolo controvento, si calcola il centro di massa e il centro delle rigidezze. Infine si calcola la ripartizione delle forze sismiche per piano e per ogni controvento, lungo l'asse x e lungo l'asse y. Essendo l'edificio preso in considerazione simmetrico e con pilastri che cambiano di sezione solamente di piano in piano, il centro geometrico combacia con quello delle rigidezze. Quindi l'edificio si deforma unicamente tramite traslazione. Il procedimento del calcolo della forza sismica è stato effettuato per ogni piano.

Successivante sono state applicate le forze nel centro geometrico di ogni piano nel modello di Sap2000.

Fatta partire l'analisi abbiamo estratto le tabelle excel da Sap2000 e abbiamo riverificato l'eccentricità dei pilastri. Quelli del primo e del secondo piano rientrano ancora nel caso di piccola eccentricità mentre quelli dei piani successivi non rientrano più nello stesso caso ma  nel caso di moderata eccentricità. I pilastri dei primi due piani risultano ancora verificati, mentre, effettuando la verifica a pressoflessione nel caso di moderata eccentricità di quelli del secondo e terzo piano, questi non risultano più verificati. Di conseguenza abbiamo verificato la sezione aumentanto le geometrie delle sezioni.

 

Abbiamo costruito il modello su SAP, sull’asse y abbiamo 3 campate da 4 m, sull’asse x abbiamo una la prima campata da 6 m, seconda, terza e quarta campata da 5 m e l’ultima è uno sbalzo laterale di 2,5 m.

 

 

 

 

 

 

 

 

 

La struttura è composta da 3 piani di 3,5 m ciascuno, con un corpo scala centrale.

In base al tipo di cemento e ai carichi strutturali inseriti sulla tabella excel, abbiamo dimensionato le nostre sezioni, e successivamente abbiamo assegnato i vincoli.

ANALISI DEI CARICHI

Successivamente abbiamo assegnato i carichi:

Carico permanente strutturale (Qs): 3,5 KN/mq

Carico permanente non strutturale (Qp): 3,5 KN/mq

Sovraccarico accidentale (Qa): 2,0 KN/mq

Combinazione SLU: Qu= (Qs x 1,3)+(Qp x 1,5)+(Qa x 1,5)= 12,05 KN/mq

PREDIMENSIONAMENTO

Distinte le travi principale dalle secondarie, abbiamo suddiviso le travi in

-Travi principali centrali

-Travi principali perimetrali

Su Excel, una volta calcolati i carichi uniformemente distribuiti su ogni trave, andiamo a inserirli sul modello di SAP. Una volta inseriti i carichi abbiamo avviato il calcolo delle sollecitazioni che ci ha mostrato la deformata e i relativi grafici degli sforzi.

DEFORMATA

 

 

 

 

 

 

 

 

SFORZO NORMALE

MOMENTO

TAGLIO

VERIFICA

Per la verifica abbiamo esportato le tabelle di SAP su Excel. Per le travi utilizziamo gli sforzi massimi presi dalle tabelle di dimensionamento, mentre per i pilastri teniamo conto dell’eccentricità.

PIANO TERRA

PRIMO PIANO

SECONDO PIANO

 

 

Ai fini dell’esercitazione abbiamo ipotizzato un edificio multipiano in calcestruzzo armato costituito da un modulo di 5x4 m e un aggetto laterale di 2 m. La struttura a telaio, costituita da travi principali, travi secondarie, pilastri e mensole, si eleva per 8 piani fuori terra. 

---

Si ipotizza che la struttura sia realizzata in c. a. ordinario, con un calcestruzzo di classe di resistenza C 28/35 ed acciaio B 450 C per l’armatura. 

Calcoliamo preventivamente le resistenze di progetto dei materiali:
- la resistenza di progetto dell’acciaio ridotta, rispetto alla tensione caratteristica di snervamento, di un coefficiente parziale di sicurezza: f_yd=f_yk/ γ_s
- la resistenza di progetto a compressione del calcestruzzo ridotta, rispetto alla resistenza caratteristica cilindrica, di un coefficiente parziale di sicurezza e di un ulteriore coefficiente riduttivo per le resistenze di lunga durata: f_cd= α_ccf_ck/ γ_c

---

Per quanto riguarda l’analisi dei carichi abbiamo fatto riferimento al dimensionamento effettuato per la prima esercitazione di un solaio in laterocemento con destinazione ad uso uffici, tenendo in considerazione la combinazione fondamentale di carico allo SLU con coefficienti parziali di sicurezza sfavorevoli. 

q_u= γ_G1 x G₁ + γ_G2 x G₂ + γ_Q2 x Q₁= 1,3 x 1,70 + 1,5 x 3,40 + 1,5 x 2,00 =10,30 kNm^-2

---

Prima di procedere al dimensionamento di massima delle travi principali e secondarie calcoliamo il carico lineare distribuito sulla trave moltiplicando il carico allo SLU ottenuto dall’analisi dei carichi per l’interasse della trave che consideriamo di 4 m per la trave principale e di 1 m per quella secondaria. Andiamo quindi a calcolare il momento massimo agente approssimando il comportamento dell’elemento a quello di una trave doppiamente appoggiata con carico uniformemente distribuito. Il momento massimo si verifica nella mezzeria e ha valore ql²/8, dove q è il carico lineare precedentemente calcolato e l è la luce della trave. 

---

Procediamo quindi al dimensionamento delle travi: ipotizziamo un valore per la base dell’elemento, pari a 30 cm per le travi principali e a 25 cm per le travi secondarie. Per calcolare l’altezza utile della sezione della trave ipotizziamo una sezione fittizia di solo cls. Costruiamo il diagramma delle tensioni imponendo che il calcestruzzo lavori al massimo e che, quindi, la sua tensione sia pari alla tensione di rottura (fcd); allo stesso modo imponiamo che la tensione dell’acciaio sia pari alla sua tensione di snervamento ridotta di un coefficiente di omogeneizzazione (da normativa pari a 15) che tiene conto dei diversi moduli di elasticità dei due materiali. Attaverso la formula del momento flettente, dato dalla coppia di forze costituita dalla risultante di compressione del cls compresso e dalla risultante di trazione dell’acciaio teso, calcoliamo l’altezza utile della sezione reagente. Quest’ultimo valore, sommato alla dimensione del copriferro posta pari a 5 cm, darà il valore minimo dell’altezza della sezione. 

 

---

Procediamo al dimensionamento delle mensole utilizzando l’analisi dei carichi e i materiali già utilizzati per la trave. Calcoliamo il momento agente considerando la mensola come una trave a sbalzo con carico uniformemente ripartito: il momento massimo si verifica in corrispondenza dell’incastro e vale ql²/2. 
Dimensioniamo la sezione ingegnerizzata seguendo gli stessi passaggi delle travi principali e secondarie. 

Dopo aver dimensionato effettuiamo una verifica di abbassamento, quindi allo stato limite di esercizio, per controllare che l’abbassamento della mensola sottoposta al carico sia minore di quello massimo ammissibile. 
Calcoliamo quindi il carico allo SLE considerando una combinazione di carico frequente: 
q_e= G₁ + G₂ + ψ_1j x Q₁= 1,70 + 3,40 + 0,5 x 2,00 = 6,1 kNm^-2 
con il coefficiente di combinazione ψ_1j = 0,5 per la categoria uffici. 
Come per le travi calcoliamo il carico uniformemente distribuito sulla mensola moltiplicando il carico allo SLE per l’interasse e sommando il peso proprio dell’elemento. 
Calcoliamo quindi il momento di inerzia della sezione rettangolare che vale I_x = (b x h³)/12. A questo punto calcoliamo l’abbassamento massimo ammissibile con la formula v_max=(ql⁴)/8EI_x che deriva dall’equazione della linea elastica. A questo punto verifichiamo che l’abbassamento della mensola rispetti i limiti di normativa e che sia quindi minore di 1/250 della luce. 

 

 

---

Dopo aver individuato il pilastro maggiormente sollecitato procediamo al dimensionamento: 
in primo luogo calcoliamo i pesi portati dal pilastro in esame, ovvero quello delle travi principali e secondarie e quello del solaio, e li moltiplichiamo per il numero di piani per ottenere lo sforzo normale agente sul pilastro. Per il calcolo utilizziamo una resistenza di progetto a compressione del calcestruzzo ulteriormente ridotta per tenere conto della fessurazione del cls. 
A questo punto calcoliamo l’area minima e la base minima della sezione del pilastro considerando una sezione quadrata. Essendo il pilastro soggetto a pressoflessione andiamo a ricalcolare la base minima necessaria affinchè l’elemento non vada in instabilità a carico di punta: calcoliamo quindi la luce libera di inflessione del pilastro considerando un coefficiente di inflessione pari a 1 in caso di elemento doppiamente incernierato. Determiniamo dunque la snellezza critica superata la quale l’asta va in instabilità da carico di punta e il raggio di inerzia minimo della sezione grazie al quale otteniamo il valore della base minima del pilastro. Siamo quindi in grado di scegliere base e altezza della sezione del pilastro. 

 

---

Dopo aver predimensionato gli elementi che costituiscono il telaio andiamo a impostare e costruire la struttura su SAP2000. Dividiamo gli elementi in gruppi in base alla loro area di influenza. Per quanto riguarda gli elementi orizzontali differenziamo travi principali centrali, travi principali perimetrali, travi secondarie e mensole. Dividiamo invece gli elementi verticali in pilastri centrali, perimetrali e angolari per ogni piano. 
Definiamo e assegniamo i vincoli alla struttura: incastri in corrispondenza dell’attacco a terra e diaphragm constraint al resto della struttura affinchè la struttura si comporti come un telaio a nodi rigidi. Procediamo quindi definendo e assegnando i materiali, le sezioni predimensionate e i carichi agenti sulla struttura. In questo caso, oltre ad assegnare i carichi permanenti e variabili già calcolati con la combinazione di carico allo SLU, introduciamo anche la forza orizzontale del vento, sia in direzione x che in direzione y.  Facciamo quindi partire l’analisi per ricavare i diagrammi e i valori delle sollecitazioni agenti sulla struttura. 

---

Una volta ricavati i valori delle sollecitazioni grazie al modello di SAP possiamo andare a verificare la struttura.
Per comodità verifichiamo solamente gli elementi piú sollecitati.
Procediamo alla verifica delle travi sottoposte a flessione retta: dobbiamo verificare che la tensione agente su ogni trave sia minore di fcd, ovvero della tensione di rottura del calcestruzzo.

---

Procediamo ora alla verifica, a flessione per quanto riguarda travi e mensole, e a pressoflessione per quanto riguarda i pilastri: dobbiamo accertarci che la tensione massima agente sia minore della tensione di rottura. Per i pilastri distinguiamo tre casi differenti in base all’eccentricità. 

 

L'intera struttura risulta verificata.

---

La struttura in cls armato di 4 piani fuori terra presenta 5 campate di 6X4 m, con degli sbalzi di 2,4 m che aggettano oltre il lato lungo delle campate e si ipotizza un uso residenziale. Per prima cosa è stata disegnato lo schema del piano tipo e le aree di influenza di travi e pilastri. L'edificio è stato modellato direttamente su SAP.

 

- Analisi dei carichi

Per eseguire il predimensionamento degi elementi che compongono il telaio è stato necessario svolgere l'analisi dei carichi. Si è preso in considerazione un solaio in laterocemento. 

- Predimensionamento

Dopo aver diviso travi principali, secondarie e mensole si sono ipotizate le geometrie delle sezioni tramite l'utilizzo delle tabelle excel inserendo l'analisi dei carichi precedendemente svolta e i dati derivanti dalla geometria dell'edificio come la luce e l'interasse delle travi. Per i pilastro si è proceduto in modo analogo.

- Analisi del modello

Una volta impostate le sezione su SAP sono stati aggiunti i carichi distribuiti utilizzando la combinazione dei carichi allo SLU e sono stati inseriti i vincoli esterni ed interni. È stata poi avviata l'analisi.

- Verifica

Dall'analisi di SAP si ricavano le tabelle con gli sforzi agenti sulle aste da esportare in excel per effettuare la verifica. Per le travi, si utilizzano le tabelle usate per il predimensionamento, inserendo questa volta i valori massimi degli sforzi ricavati da SAP. I pilastri si verificano tenendo conto dell'eccentricità. In questo caso specifio, alciune travei principali, di sezione rettangolare 30x60, non sono verificate. Per risolvere il problema è necessario utilizzare una classe di calcestruzzo più resistente oppure aumentare l'altezza delle travi.

Pilastri

 

Studentesse: Elena Santacesaria, Benedetta Schettini.

Il fine di questa seconda esercitazione è quello di considerare un edificio multipiano con una struttura composta da telai piani in cls armato (le travi collaborano con i pilastri) e dunque di dimensionare i suoi elementi: travi, pilastri, mensole.

MODELLO

Per prima cosa abbiamo costruito la struttura da analizzare direttamente su SAP2000, partendo da una griglia regolare di 4x3 campate (di 5x4m ciascuna) e uno sbalzo laterale di 2m. La struttura si sviluppa su 3 piani di 3m ciascuno, con un corpo scala centrale. Per la definizione del modello iniziale siamo partite da un'assegnazione preliminare di massima delle sezioni dei vari elementi, che poi verranno adeguatamente verificati. Altro passaggio fondamentale è stato quello di assegnare i vincoli a terra, che in una struttura a telaio rigido in cls sono tutti incastri. Una volta definito il modello siamo passate al predimensionamento degli elementi.

ANALISI DEI CARICHI

Prima di tutto, per poter dimensionare gli elementi, è necessario conoscere il carico q che grava su questi e dunque procedere con l'analisi dei carichi che consente di conoscere l'entità della forza agente sui componenti della struttura. Abbiamo ipotizzato l'utilizzo di un solaio in latero-cemento.
Carico permanente strutturale (travetti, pignatte, soletta):
Qs= 3,5 KN/mq
Carico permanente non strutturale (intonaco, massetto, malta, pavimentazione, incidenza tramezzi):
Qp=3,0 KN/mq
Sovraccarico accidentale (definito in base alla destinazione d'uso, nel nostro caso residenziale):
Qa=2,0 KN/mq

Abbiamo dunque calcolato la combinazione allo SLU con i rispettivi coefficienti: Qu= (Qs*1,3)+(Qp*1,5)+(Qa*1,5) ottenendo: Qu=12,05 KN/mq

PREDIMENSIONAMENTO

Travi
Per prima cosa, ragionando sull'orditura del solaio, abbiamo distinto le travi principali dalle secondarie. Successivamente, in base alle rispettive aree di influenza di solaio agente su di esse, le abbiamo ulteriormente distinte in:
-Travi principali centrali (più sollecitate, hanno l'area di influenza maggiore)
-Travi principali perimetrali (con area di influenza dimezzata)
-Travi secondarie centrali
-Travi secondarie perimetrali

Vedremo in seguito che le travi perimetrali, principali e secondarie, sono soggette ad un carico ulteriore che è quello del tompagno e dunque una suddivisione più corretta sarebbe:
-Travi principali centrali e travi principali perimetrali che portano il tompagno
-Travi secondarie che portano solo se stesse e travi secondarie che portano il tompagno (confermando che non sono mai scariche).

Da queste considerazioni siamo passate su Excel. Una volta calcolato il carico uniformemente distribuito su ogni trave, ricaviamo il momento flettente massimo che agisce su di esse (ricordando che nel caso di una trave doppiamente appoggiata si trova nella sezione di mezzeria e dunque vale: Mmax: (Qu*l^2)/8), il valore della resistenza a compressione del cls (fcd) e quella dell'acciaio di armatura (fck). Tramite questi ultimi valori abbiamo ricavato i parametri β (la cui formula definisce il rapporto tra l'altezza utile hu e l'asse neutro) ed r.
Fissate in precedenza le dimensioni della base, nel nostro caso 30cm sia per le travi principali che secondarie, abbiamo ottenuto l'altezza utile alla quale è stata aggiunta la dimensione del copriferro, per conoscere infine l'altezza minima di progetto, successivamente ingegnerizzata (Hmin=hu+δ). Per ultimi abbiamo calcolato l'area della sezione e subito dopo, conoscendo il peso specifico del cls, il peso unitario, valore importante che è stato sommato al Qu per capire se le dimensioni della sezione consentono alla trave di resistere anche sommando al carico ultimo il peso proprio dell'intero elemento.

Mensole

I medesimi passaggi svolti per il predimensionamento delle travi sono stati eseguiti anche per quanto riguarda le mesole. Definita l'area di influenza ed il carico uniformemente distribuito che grava su di esse, abbiamo raggiunto il valore massimo del momento agente (che non è più quello di una trave doppiamente appoggiata, ma trattandosi di mensole, in corrispondenza della sezione di incastro vale: Mmax=(Qu*l^2)/2). Stabilite le dimensioni della sezione, 30x45cm nel nostro caso, abbiamo effettuato una verifica a deformabilità controllando che l'abbassamento massimo dell'elemento fosse minore del 2% della distanza massima dall'appoggio. Questo procedimento è stato effettuato allo SLE per verificare che non vi siano deformazioni capaci di limitare l'efficienza della costruzione.

Pilastri

Anche in questo caso è stato fondamentale cominciare con l'individuazione e il calcolo delle varie aree di influenza. Per ogni piano abbiamo distinto 3 categorie di pilastri:
-angolari
-perimetrali 
-centrali (quelli centrali del piano terra saranno sicuramente i più sollecitati poichè su questi verranno trasmessi tutti i carichi dei piani superiori)

Passando dunque su Excel, nel compilare la tabella questa volta abbiamo dovuto tener conto del fatto che su questi elementi il carico non è uniformemente distribuito, bensì concentrato, e considera la somma dei carichi agenti di solaio, travi principali e secondarie (tiene conto quindi della possibilità di rottura del materiale per schiacciamento e della possibilità che si verifichi il fenomeno di instabilità).

Arriviamo così a definire uno sforzo normale massimo verosimile che dipende dal carico dovuto al peso proprio delle travi che si poggiano in testa al pilastro, dal carico del solaio e dal numero dei piani dell'edificio. A partire dalla resistenza di progetto del materiale fcd, abbiamo ricavato di conseguenza l'area di sezione minima del pilastro affinchè non si verifichi lo schiacciamento del materiale.

Da questo momento in poi è subentrato il concetto di snellezza, e abbiamo dimensionato considerando anche il momento flettente, poichè sappiamo che i pilastri sono elementi soggetti a pressoflessione. Abbiamo stabilito quindi il valore massimo di snellezza, usando la luce libera di inflessione (che tiene conto di come il pilastro è vincolato) e il modulo di elasticità del cls, e da questa il valore minimo del raggio di inerzia necessario al fine di evitare il fenomeno dell'instabilità euleriana.

Determinate quindi la base e l'altezza minima abbiamo definito la sezione effettiva di progetto ed è stato poi necessario verificare a pressoflessione il pilastro, imponendo che la tensione massima a cui è sottoposto siamo minore o uguale alla resistenza di progetto del materiale.

Modello

Dopo aver predimensionato tutti gli elementi del telaio siamo tornate al modello su SAP2000, per agevolare il lavoro abbiamo diviso gli elementi in vari gruppi, e infine riassegnato correttamente le sezione calcolate precedentemente, avendo già definito il materiale. Per assegnare i carichi uniformemente distribuiti abbiamo creato una combinazione di carichi SLU (da Define/Load Combination) che tiene conto dei carichi sopracitati Qs, Qp, Qa, del peso proprio PP degli elementi e del G2, il peso del tompagno che grava sulle travi perimetrali e che è stato aggiunto nella combinazione come carico lineare insieme agli altri. Per ultimo è stato applicato il diaphram per simulare al meglio la condizione di telaio rigido.

Terminato il modello abbiamo avviato l'analisi e ottenuto così la configurazione deformata.

DIAGRAMMA SFORZO NORMALE

DIAGRAMMA TAGLIO 2-2

DIAGRAMMA TAGLIO 3-3DIAGRAMMA MOMENTO 2-2

DIAGRAMMA MOMENTO 3-3

Abbiamo infine esportato le tabelle su Excel, divise in gruppi, e per ciascuno abbiamo preso gli sforzi massimi e verificato le sezioni.

VERIFICA

Terminata l'analisi è stata fatta la verifica degli elementi progettati sostituendo però le sollecitazioni di progetto con quelle ottenute da SAP2000. La verifica mette a confronto le tensioni agenti sulla sezione più sollecitata con le tensioni ammissibili: σmax ≤ fcd

Verifica travi a flessione

Per la trave la tensione massima è stata calcolata come rapporto tra momento massimo e modulo di resistenza a flessione massimo:  σmax= Mmax/Wmax    Mmax/Wmax≤ fcd

Verifica mensole

Verifica pilastri a pressoflessione

Per il pilastro la tensione massima è fornita dallo sforzo normale di compressione e dal momento flettente trasmesso dalla trave al pilastro: σmax= N/A+Mmax/Wmax
Da cui la verifica di una sezione presso inflessa: N/A+Mmax/Wmax≤ fcd.

In base ai valori di N e M ottenuti da SAP2000 abbiamo capito in quale tabella inserirci, ovvero se ci troviamo nel caso della piccola, moderata o grande eccentricità.

Al piano terra e al primo piano abbiamo riscontrato un'eccentricità piccola poiché i pilastri sono maggiormente soggetti a sforzo normale di compressione.

Al secondo piano abbiamo riscontrato alcuni pilastri con eccentricità moderata in quanto l'aumento dell'eccentricità è dovuto al decremento dello sforzo Normale che grava sui pilastri.

 

        

 

• MODELLAZIONE DEL TELAIO

Per la modellazione dell’edificio è stato utilizzato direttamente il software di SAP2000 andando, in seguito al predimensionamento delle sezioni, ad assegnare le informazioni relative al materiale, alle sezioni degli elementi e ai carichi verticali ed orizzontali. Innanzitutto è stata disegnata la struttura del primo livello e poi replicata in altezza fino ad ottenere l’altezza prestabilita dell’edificio. Essendo un telaio di elementi verticali e orizzontali tra loro collegati da nodi rigidi, assegno un vincolo interno (Assign/Joint/Constraint/Diaphragm) e ai pilastri del piano terra il vincolo di incastro esterno al terreno. Assengnando il diaphragm, si impone a tutti i punti un’unica rotazione attorno all’asse z, in modo da ottenere un impalcato rigido.

Per facilitare l’assegnazione delle sezioni ottenute dal predimensionamento degli elementi verticali e orizzontali, si creano dei gruppi di selezione per le travi e i pilastri.

• PREDIMESIONAMENTO DELLE TRAVI 

Procedo con individuare le aree di influenza delle travi e misurarne l’interasse.

 

       

Scelto il solaio in laterocemento dell’impalcato ne considero un metro quadro di normativa per calcolarne il peso. Per definire la combinazione di carico allo stato limite ultimo SLU devo tener conto dei coefficienti di sicurezza.

• q_s = 3,50 KN/m²

• q_p = 3,00 KN/m²

• q_a = 2,00 KN/m²

• q_u = q_s x 1,3 + q_p x 1,5+ q_a x 1,5 = 12,05 KN/m²

Calcolato il carico del solaio, espresso come densità di carico superficiale in [KN/m² ], lo moltiplico per l’interasse trovando il carico lineare incidente sulle travi q_trave [KN/m].

q _trave = q_solaio x l

Per vedere quali siano le travi più sollecitate, considero il valore più grande del momento M_max sulle travi soggette a flessione  . Il momento massimo si calcola con il carico q_trave per la luce della trave. Per una trave doppiamente appoggiata il M_max è ql²/ 8 .

Per determinare l’altezza utile h_u , ovvero la distanza tra il lembo superiore del cls compresso e il baricentro delle armature tese, ho bisogno di alcuni dati e di fissare la misura della base. La formula di progetto è h_{u =} r x √ (M_max/ b ). I dati di cui ho bisogno sono le resistenze caratteristiche dell’acciaio e del cls per ricavare le tensioni di progetto relative al materiale e i moduli elastici da cui ricavo il coefficiente di omogenizzazione. Impongo che la tensione di progetto del cls sia uguale alla tensione massima nella trave, per poterla dimensionare e trovare l’altezza ingegnerizzata H_ing .

Scelgo un acciao di armatura S450C e un cls C28/35.

• f_yd = f _yk / 1,15

• f_cd = ( f_ck / 1,5 ) x 0,85

• r = √( 2 / ( f_cd ( 1 - beta / 3 ) beta ) ) 

• beta = f_cd / ( f_cd  + (  f_yd / n ) )

• n = Ef / Ec =  15       Coefficiente di omogenizzazione 

Trovate le tensioni di progetto posso determinare l’altezza utile h_u e, sommandola al copriferro, calcolare l’altezza minima che deve avere la sezione per non inflettersi.

• Hmin = h_u + delta

  

Per verificare se la sezione ingegnerizzata sia in grado di tenere il peso proprio e i carichi, aggiungo al carico totale del solaio il peso unitario della trave ( Peso specifico del cls moltiplicato all’area della sezione ) e lo motiplico per il 1,3. Considerando il peso proprio della trave, la sezione H_ing risulta comunque maggiore dell’altezza minima e la verifica è soddisfatta.

• PREDIMESIONAMENTO DELLE TRAVI A SBALZO

Il procedimento di progetto è uguale al precedente, calcolato il carico lineare posso determinare il momento massimo flettente per la formula dell’altezza utile h_u .

Una volta verificata la sezione ingegnerizzata, che deve essere maggiore della h_u, devo verificare che la trave non si abbassi troppo. La verifica degli abbassamenti si effettua allo stato limite d’esercizio e bisogna verificare che l’abbassamento massimo v_max sia maggiore di un certo limite di deformabilità di 1/250 della luce della mensola. Il valore dell’abbassamento si può calcolare con l’equazione della linea elastica che tiene in considerazione il momento flettente della mensola M_max = ql²/ 2, il modulo elastico della trave E_cls e momento d’inerzia I_x = b x h³ / 12 per sezioni rettangolari.  

• PREDIMESIONAMENTO DEI PILASTRI

Si è proceduto individuando l’area di influenza di ciascun pilastro. Il pilastri maggiormente sollecitati sicuramente saranno quelli al piano terra, poiché su questi verrano trasmessi tutti i carichi dei piani superiori.

                         

L’area di influenza ha come dimensioni L_p e L_s e varia in base alla posizione dei pilastri se posti centralmente, perimetralmente o angolarmente. Calcolata l’area osservo che quelli più sollecitati saranno i pilastri centrali, quelli con l’area di influenza maggiore e quindi con sforzo normale maggiore. Per determinare lo sforzo normale di compressione N, vado a considerare sia il peso delle travi sia il peso del solaio relativo all’area di influenza. Il peso delle travi, gravante nell’area di influenza dei pilastri, si ricava sommando i contributi di ogni trave e moltiplicando per 1,3.

• q_trave = ( trave_p + trave_s ) x 1,3                                               [ KN/m ]

Il carico dovuto al solaio si ricava dalla combinazione allo stato limite ultimo del carico strutturale, di quello permanente e di quello accidentale, il tutto moltiplicato per l’area di influenza per ottenere una forza concentrata.

• q_solaio = ( q_s x 1,3 + q_p x 1,5+ q_a x 1,5 ) x A                            [ KN/m₂] x [ m₂ ] = [ KN ]​

A questo punto posso calcolare la forza di compressione sommando il q_trave e il q_solaio e moltiplicando per il numero dei piani. Una volta ricavato lo sforzo di compressione sui pilastri posso dimensionare la sezione uguagliando la tensione massima nella trave alla resistenza di progetto del materiale e ottenere l’area minima che deve avere la sezione per evitare la rottura.

• f_cd = sigma _max                      sigma _max = N / A

• f_cd = N / A

• A _min = N / f_cd​

Per elementi strutturali in cls armato le sezioni dei pilastri sono rettangolari e la formula della base minima è 2√3 x p_min ovvero in funzione della snellezza del pilastro. Per trovare il raggio minimo di inerzia devo prima deteminare la snellezza e la luce libera di inflessione che tiene conto dei vincoli a cui è soggetto il pilastro .

• lamba = π √ (E / f _cd )                     l₀ = l x beta

• p_min = √ (l₀ / lamba )

Trovato il raggio di inerzia calcolo la base minima b_min e la sovradimensiono nell’ingegnerizzazione. Per dimensionare l'altezza minima della sezione h_min ,divido la base ingegnerizzata per l’area precedentemente calcolata nel dimensionamento a resistenza. L'altezza ingegnerizzata descrive la sezione rettangolare del pilastro in cls armato, da cui si ricava l’area di progetto Adesign.

• h_min= b / A _min

Si è scelto di adottare sezioni di lato non inferiore a 30 cm e dunque di area non inferiore a 900 cm² . Le sezioni dimensionate sono 50 x 30 cm, 40 x 30 cm e 30 x 30 cm rispettivamente per i pilastri del piano terra, primo piano e piano secondo. Per la verifica della sezione poiché nel cemento armato il nodo rigido tra trave e pilastro trasmette momento, il pilastro deve resistere a pressoflessione.

•ANALISI DEL TELAIO DIMESIONATO IN SAP

Per la verifica a pressoflessione dei pilastri è stato necessario introdurre il telaio su SAP per ricalcolare correttamente le sollecitazioni della struttura. Dopo aver effettuato il predimesionamento degli elementi strutturali sui fogli di calcolo di excel, ne è stata effettuata l'assegnazione delle sezioni sul modello di SAP precedentemente creato.

Come prima cosa, avendo dimensionato sezioni rettangolari, per i pilastri si dovrà tener conto dell'orientamentamento e quindi del valore del momento di inerzia che inciderà sulla rigidezza traslante del telaio. Si è provveduto a ruotare i pilastri perimetrali posti lungo l'asse Y ( sistema globale ) andando a ruotare di 90° gli assi locali degli elementi. In questo modo il momento d’inerzia aumenta in quanto la base e l'altezza sono invertite e di conseguenza maggiore sarà la rigidezza.

• SOLLECITAZIONI MASSIME

Definisco il valore dei carichi lineari, ottenuti dai fogli excel, e li assegno alle travi che trasmetteranno momento ai pilastri. Alle perimetrali è stato aggiunto il contributo del tompagno. Il carico della tamponatura esterna in laterizio forato è stato calcolato prima al metro quadro e moltiplcato poi per l'interpiano netto ovvero l'altezza del pilastro. Nell'analisi delle sollecitazioni considero anche le forze orizzontali del vento lungo la direzione X e Y . L'azione del vento agisce sulle tamponature dei piani e da queste viene trasmesso ai pilastri sottoforma di carico distribuito linearmente lungo l'altezza.

 

Per ricavare le sollecitazioni massime e verificare le sezioni dimensionate, seleziono i pilastri in base ai gruppi mandando l'analisi con COMBO_Y e COMBO_X per valutare quale sia la condizione più gravosa. Dall'analisi i valori di COMBO_X risultano simili alla combinazione SLU per questo si è scelto di considerare solo l'azione del vento agente sul sopravento maggiore.

• VERIFICA DEI PILASTRI A PRESSOFLESSIONE

Dopo aver mandato l'analisi con i carichi verticali e orizzontali, ricavo le nuove sollecitazioni di progetto che andrò ad inserire nella tabella excel ai fini dell'assegnazione dei pilastri nelle tabelle della piccola, moderata e grande eccentricità. Per suddividere i pilastri nelle tre eccentricità è stata fatta una tassonomia in base al piano e sono stati individuati i pilastri in pianta per distiguerli in base all'orientamento ( per i pilastri ruotati è stato condiserato M attorno all'asse locale 2). Sono stati quindi inseriti i pilastri nel file excel di verifica della pressoflessione. In base al rapporto tra N e M si ricava il valore dell'eccentricità e si confronta il valore ottenuto con h/6 e h/2 .

I pilastri del piano terra risultano tutti in piccola eccentricità, quelli del primo piano rientrano sia nella moderata che nella piccola mentre quelli dell'ultimo piano ricevendo una sforzo di compressione minore avranno l'eccentricità più grande. Una volta classificati in base all'eccentricità, per verificare il pilastro a pressoflessione si deve imporre che la tensione massima sia minore della resistenza di progetto.

• sigma_max ≤ f_cd

La tensione massima può essere calcolata in funzione dello sforzo normale di compressione e il momento.

• sigma_max = N / A + M / W_max

Dalla verifica risultano non verificate le sezioni 30 x 30 cm di quattro pilastri dell'ultimo piano. Cambiando le dimensioni della sezione con 40 x 40 cm la verifica risulta soddisfatta.

 

           

 

 

Esercitazione 2: Dimensionamento struttura a telaio in C.A.

Iniziamo con il disegno su Autocad della pianta del solaio del caso di progetto, con le seguenti dimensioni: 24m lungo l’asse x, 12m lungo l’asse y, 3,5m lungo l’asse z (altezza interpiano), con 3 piani totali. Il corpo scala misura 4mx2,4m, con un’alzata di 17,5cm, una pedata di 28cm e il pianerottolo 1,2mx2,4m. Lo sbalzo lungo l’asse x misura 2m.

 

Ora raggruppiamo le aree d’influenza Ai dei pilastri e le calcoliamo.

Passiamo su SAP2000 e procediamo al ridisegno della struttura.

 

A questo punto iniziamo con il pre-dimensionamento della trave principale, scegliendo innanzitutto il materiale da SAP C28/35.

Dal foglio Excel abbiamo modificato l’interasse e la luce e Fck (28). Mettendo come base b 30cm, come altezza h 55cm, la sezione è verificata.

 

Su SAP, aggiungiamo una nuova sezione chiamata TRAVE PRINCIPALE (rosso), con il materiale scelto C28/35 e gli riportiamo le dimensioni ottenute dal foglio Excel (h0,55 b0,3).

Tornando al foglio Excel passiamo alla seconda trave, modificando l’interasse e la luce e Fck(28). Scegliendo come base b25 cm, come altezza h 35cm, la sezione risulta verificata.

Su SAP, definiamo una nuova sezione chiamata TRAVE SECONDARIA (arancione), con il materiale scelto C28/35 e gli riportiamo le dimensioni ottenute dal foglio excel (h0,35 b0,25).

Passiamo al dimensionamento delle mensole tramite il foglio Excel, qui modifichiamo i valori base b 30cm e altezza h 50cm, così la sezione risulta verificata.

Definiamo una nuova sezione su SAP chiamata MENSOLA(verde) dello stesso materiale C28/35 ma con altezza h 50cm e base b 30cm, così da foglio Excel.

Ora dobbiamo definire il peso delle travi principali e secondarie che poggiano sul pilastro. Su SAP utilizziamo i comandi: DEFINE-SECTION PROPERTIES-SHOW MATERIALS, da lì vediamo il peso per unità di volume (25).

Sul foglio excel, nel peso della trave principale facciamo l’operazione =25*0,3*0,55 e otteniamo il peso in kN/m 4,13. Ripetiamo l’operazione per la trave secondaria e otteniamo il peso in kN/m 2,19. Copiamo la fila per il numero dei piani (3). Aggiungiamo il modulo elastico E alla tabella (32308 Mpa).

Abbiamo definito la sezione dei tre pilastri dei vari piani:

• (PT=40cmx40cm)
• (P1=35cmx35cm)
• (P2=30cmx30cm)

 

Su SAP, definiamo i pilastri.

 

Definiamo travi principali centrali(TP_C), principali perimetrali (TP_P), secondarie (TS).

Aggiungiamo nuove sezioni per il corpo scala: cordolo (SCALA_CORDOLO: cyano), ginocchio (SCALA_GINOCCHIO: rosa antico), montanti (SCALA_MONTANTI: rosso vino).

Disegniamo dalla vista 3d il corpo scale, e creiamo un unico gruppo che contenga tutti gli altri (SCALE: viola). Assegniamo le sezioni alle travi principali, secondarie, mensole e pilastri. Separiamo la trave principale nel punto di congiunzione con il cordolo della scala.

 

Una volta copiato il modello e aver creato i piani superiori ci mettiamo in vista 3d x-y con apertura 0 e assegniamo i frame dei piani 1-2 ai gruppi che abbiamo creato per il piano terra.

Ora definiamo i vincoli, assegnando un incastro per ogni pilastro a terra.

Selezioniamo tutte le travi di ogni piano attraverso la 2d view con z ad altezza di ogni rispettivo piano 3,5-7-10,5 e gli assegniamo la condizione di impalcato tramite il comando Diaphram.

Passiamo a definire i casi di carico creando i seguenti load patterns: Qa (moltiplicatore di peso proprio 0), Qp (moltiplicatore di peso proprio 0), Qs (moltiplicatore di peso proprio 0), PP (moltiplicatore di peso proprio 1). 

Si definisce poi un load combination con tutti questi carichi, ognuno moltiplicato per il proprio coefficiente maggiorativo da normativa:

• PP: Scale factor = 1,3
• Qs: Scale factor = 1,3
• Qp: Scale factor = 1,5
• Qa: Scale factor = 1,5

Consideriamo ora i carichi di tamponatura: tramezzi, muri pieni, muri con finestre e muri con porte e finestre.

Consideriamo il carico sulla scala: gradini e pianerottolo.

Inoltre, a tutto ciò va aggiunto il peso variabile.

Moltiplichiamo i carichi Qp, Qs, Qa per l’interasse:

Qs*I   3,5x2 = 7 kN/m

Qp*I  3,0x2 = 6 kN/m          

Qa*I  2,0x2 = 4 kN/m

Qu = 12,05 kN/m

Calcoliamo il carico sulle travi principali perimetrali

Qtpp = 39,35 Kn/m   Qtpc (senza scala) = 52,2 Kn/m  Qtpc (con scala) = 26,1 kN/m

Calcoliamo il carico sulle travi secondarie perimetrali

Qtspm = 14,02 kN/m  Qtspb = 15,62 kN/m

Trave secondaria balcone 5,25x0,5 = 2,6 kN/m

Trave secondaria centrale (senza scale)  Qtsc 9,5 kN/m

Trave secondaria centrale (con scale)  Qtsc 6,52 kN/m

Trave principale perimetrale (mensola)  Qtpcpm 5,25 kN/m*2 = 10,5 kN/m

Trave principale centrale (mensola)  Qtpcm 5,25 kN/m*4 = 21 kN/m

Calcoliamo la trave a ginocchio: Pianerottolo-trave 6 kN/m      Qtgp = 8,16 kN/m     Qg = 9 kN/m

A questo punto creiamo i load patterns con i carichi distinti per travi principali (con e senza scala), perimetrali e centrali secondarie (con e senza scala), mensola con balcone. Specifichiamo i carichi con finestre o muro pieno. Q per la scala sul pianerottolo e la trave a ginocchio.

 

PP*1,3

Qs*1,3

Qp*1,5

Qp*1,5

CARICHI:

• Tramezzi = 1kN/m²
• Muro = 10kN/m²
• Finestre = 8kN/m²
• Muro con porte e finestre = 7kN/m²
• Gradini = 2,5kN/m²
• Pianerottolo = 5kN/m²
• Peso variabile = 1,8kN/m²

NOTA: la moltiplicazione per il coefficiente di sicurezza (SCALE FACTOR) è stata fatta preventivamente, successivamente è stato moltiplicato il peso proprio PP con il coefficiente di sicurezza nella LOAD COMBINATIONS.

Assegniamo i carichi creati (DISTRIBUTED LOADS)

(NEL FILE PDF SI TROVANO GLI SCREENSHOT APPROFONDITI PER OGNI CASO DI CARICO)

Su Autocad disegniamo le piante indicanti i carichi con le rispettive Aree d’influenza Ai delle travi.

A questo punto possiamo avviare l’analisi.

Visualizziamo la struttura deformata tramite il comando SHOW DEFORMED SHAPE.

 

Ora, tramite il comando SHOW FORCES/STRESSES-FRAMES/CABLES/TENDONS, visualizziamo i diagrammi del momento in XZ.

Ora il diagramma dello sforzo assiale dei pilastri.

Ora mettiamo in evidenza i diagrammi del momento 33 con i relativi valori scaturiti dall’analisi.

Vista XZ:

 

YZ:

Infine, posizioniamo la vista trasversale dal lato opposto inserendo 24m come valore sull’asse X, affinché si vedano i diagrammi della facciata con gli sbalzi.

YZ:

 

Per visualizzare le tabelle: Display – Show Tables, scegliamo i casi di carico con Select Load Patterns e spuntiamo ANALYSIS RESULTS.

Nella tabella che si apre scegliamo Elements Forces/Frames, valori che saranno utilizzati per il successivo dimensionamento.

 

Visualizziamo i diagrammi su SAP:

• Trave principale

 

• Mensole

 

PILASTRI

PILASTRI P.T. CENTRALI IN CLS28/32 (40x40)   FRAME 49

• N = 2952 kN
• M = 31,6
• e = M:N = 0,010m à 1cm

1cm < H/6  PICCOLA ECCENTRICITÀ

Fcd = 15,9 Mpa

I (Momento d’Inerzia) = (b*hᶟ)/12 = 213333,33 mᶟ

Wx (Modulo di resistenza a flessione) = (b*h²)/6 = 10666,66 mᶟ

σN = (N*10):A = 18,45 Mpa

σm = (M*1000):Wx = 2,96 Mpa

σMax = 21,41 Mpa > fcd  NON VERIFICATO (dobbiamo scegliere pilastri rettangolari)

PILASTRI CENTRALI PIANO PRIMO (35x35)   FRAME 117

• N = 1998,8 kN/m
• M = 47,83 kN/m
• e = M:N = 0,24m à 24cm à H/6 < 24cm < H/2 MODERATA ECCENTRICITÀ

Fcd = 15,9 Mpa

I = bhᶟ/(12) = 125052, 08 cm⁴

Wx = bh²/6 = 7145, 83 cm³

σN = 16,27 Mpa

σM = 4,48 Mpa

σMax = σN + σM = 20,75 > fcd   NON VERIFICATA (dobbiamo scegliere un pilastro a sezione rettangolare)

PILASTRI CENTRALI PIANO 2 (30x30) FRAME 185

• N = 1012,4 kN
• M = 33,42 kN/m
• e = M:N = 0,33m à 33cm à H/6 < 33cm < H/2 MODERATA ECCENTRICITÀ

fcd = 15,9 Mpa

I = bhᶟ/(12) = 67500 Mpa

Wx = bh²/6 = 4500 Mpa

σN = 11,24 Mpa

σM = 7,42 Mpa

σMax = σN + σM = 18,66 > fcd   NON VERIFICATA (dobbiamo scegliere un pilastro a sezione rettangolare)

Render:

Studentesse: Elisa Meta, Alessia Silvestri

Studentesse: Mariani Lucia, Maurelli Ilaria

Progetto della geometria
Abbiamo progettato un edificio regolare in calcestruzzo armato con le seguenti caratteristiche:
Dimensioni della pianta: 22,00x12,00 metri
- Altezza totale: 10,50 metri
- Altezza interpiano: 3,50 metri
- Numero di piani: 3
- Lievi aggetti: mensole di 2,00 metri
- Gabbia scala con travi a ginocchio di dimensioni  2,50x4,00 metri
- Comportamento a telaio

 

 

Analisi dei carichi
Dopo aver definito la geometria, abbiamo definito i carichi superficiali distribuiti su un metro quadrato di solaio che, dopo essere stati convertiti in carichi linearmente distribuiti, dovranno essere assegnati alle aste orizzontali.
Queste ultime sono state differenziate, dopo aver definito l'orditura del solaio, in travi principali e travi secondarie e, successivamente, sono state suddivise anche in base al carico agente su di esse.

Tassonomie delle travi
- Travi principali perimetrali
   Interasse 2,00 metri
   (Portano il peso proprio, il peso del solaio e il peso del tompagno)
- Travi principali centrali
   Interasse 4,00 metri
   (Portano il peso proprio e il peso del solaio) 
- Travi secondarie perimetrali
   Interasse 0,50 metri
   (Portano il peso proprio e il peso del tompagno)
- Travi secondarie centrali
   Interasse 1,00 metri
   (Portano il peso proprio)

Abbiamo quindi calcolato i carichi agenti su un metro quadrato di solaio suddividendoli nelle tre categorie
- Carico permanenti strutturali
- Sovraccarico permanente non strutturale
- Carico accidentali

Analisi dei carichi di un solaio in laterocemento

1. Pavimentazione in parquet
   2 cm = 0,02 m
2. Massetto
   3,00 cm = 0,03 m
3. Isolante
   4,00 cm = 0,04 m
4. Soletta collaborante
   5,00 cm = 0,05 m 
5. Pignatte
   20,00 cm = 0,20 m
6. Travetti
   20,00 cm = 0,20 m
7. Intonaco
   1,50 cm = 0,015 m

​Spessore totale solaio = 35,50 cm = 0,355 m

Calcolo del carico distribuito superficiale

1. 0,02 m x 7,20 KN/m³ = 0,144 KN/m²
2. 0,03 m x 20,00 KN/m³ = 0,60 KN/m²
3. 0,04 m x 0,20 KN/m³ = 0,008 KN/m²
4. 0,05 m x 25,00 KN/m³ = 1,25 KN/m²
5. 2 (0,20 x 0,12 x 1,00) KN/m³ x 25 KN/mc = 1,20 KN/m²
6. 2 (0,38 x 0,20 x 1,00) m³/m² x 15 KN/mc = 2,28 KN/m²
7. 0,015 m x 18,00 KN/m³ = 0,27 KN/m²

- Carico strutturale q_s
   Soletta + Travetti + Pignatte
   1,25 KN/m² + 1,20 KN/m² + 2,28 KN/m² = 4,73 KN/m²
- Sovraccarico permanente q_p
   Parquet + Massetto + Isolante + Intonaco + Incidenza impianti + Incidenza tramezzi
   0,144 KN/m² + 0,60 KN/m² + 0,008 KN/m² + 0,27 KN/m² + 0,50 KN/m² + 1,00 KN/m² = 2,52 KN/m² = 2,52 KN/m²
- Carico accidentale q_a
   Dato fornito dalla normativa in base alla destinazione d’uso = 2,00 KN/m²

A questo punto abbiamo considerato le combinazioni di carico fornite dalla normativa per le verifiche agli stati limite, utilizzando coefficienti parziali di sicurezza sfavorevoli.

Combinazione di carico allo stato limite ultimo SLU
γs qs + γp qp + γa qa = 1,30 x 4,73 KN/m² + 1,50 x 2,52 KN/m² + 1,50 x 2,00 KN/m² = 12,89 KN/m² = 12,90 KN/m²
q_u = 12,90 KN/m²
Combinazione di carico allo stato limite d’esercizio SLE
γ̃s qs + γ̃p qp + γ̃a qa = 1,00 x 4,73 KN/m² + 0,70 x 2,52 KN/m² + 0,70 x 2,00 KN/m² = 7,88 KN = 7,90 KN/m²
qe = 7,90 KN/m²

Successivamente abbiamo calcolato il carico linearmente distribuito del tompagno che andrà a gravare sul perimetro dell’edificio (travi principali perimetrali, travi secondarie perimetrali)

Analisi dei carichi del tompagno 

1. Intonaco esterno
   2,00 cm = 0,02 m
2. Isolante
   5,00 cm = 0,05 m
3. Rasante
   1,00 cm = 0,01 m
4. Blocchi in laterizio forati
   20,00 cm = 0,20 m
5. Intonaco interno
   2,00 cm = 0,02 m

Spessore totale tompagno = 30,00 cm = 0,30 m
Altezza totale tompagno =
(altezza interpiano) - (spessore del solaio) =
350,00 cm - 35,50 cm = 314,50 cm = 3,145 m

Calcolo del carico distribuito lineare
0,02 m x 3,145 m x 18,00 KN/m³ = 1,13 KN/m
0,05 m x 3,145 m x 0,20 KN/m³ = 0,03 KN/m
0,01 m x 3,145 m x 0,30 KN/m³ = 0,009 KN/m
0,20 m x 3,145 m x 8,00 KN/m³ = 5,00 KN/m
0,02 m x 3,145 m x 18,00 KN/m³ = 1,13 KN/m
Peso totale tompagno = 7,299 KN/m = 7,30 KN/m

Infine, grazie moltiplicando i carichi superficiali ottenuti rispettivamente per gli interassi delle membrature su cui agiscono, abbiamo ottenuto i carichi linearmente distribuiti da assegnare su SAP.

Carico dovuto al vento

Per quanto riguarda gli elementi strutturali verticali, abbiamo considerato un contributo del vento pari a 0,50 KN/m² e, dopo aver suddiviso i pilastri in base al loro interasse, abbiamo calcolato il carico distribuito verticale agente su ogni pilastro nelle due direzioni x e y.

Tassonomie dei pilastri
- Pilastri perimetrali
   Interasse 5,00 metri
   (Subiscono il carico trasmesso dal solaio alle travi principali e l’azione orizzontale del vento lungo le due direzioni x e y)
- Pilastri angolari
   Interasse 2,50 metri
   (Subiscono il carico trasmesso dal solaio alle travi principali e l’azione orizzontale del vento lungo le due direzioni x e y)
- Pilastri centrali
   (Subiscono il carico trasmesso dal solaio alle travi principali per tutti i piani sovrastanti)

Pre dimensionamento
Per il pre dimensionamento delle membrature ci siamo basate su tre modelli fondamentali di aste:
- Mensola verticale
- Trave doppiamente appoggiata
- Mensola orizzontale

Pilastri
Modello: mensola verticale
Per pre dimensionare gli elementi strutturali verticali che compongono il nostro edificio, abbiamo per prima cosa effettuato il calcolo per la base minima di un pilastro in calcestruzzo di altezza 3,50 m
b_min = 2√3ρ_min = 2√3 x 3,33 cm = 11,55 cm
Dividendo il valore dell'area minima ottenuta per questo valore della base, abbiamo trovato la dimensione minima dell'altezza del pilastro
h_min = 159,00 cm² / 11,55 cm = 13,77 cm
Il pre dimensionamento è stato effettuato considerando una dimensione della base e dell'altezza dell'elemento maggiore rispetto alle dimensioni minime trovate in quanto, data l’entità della struttura e sulla base delle precedenti esercitazioni effettuate su SAP, il valore minimo risultava troppo piccolo per poter costituire la base di un pilastro in grado di resistere alle sollecitazioni agenti.
Lo sforzo di compressione utilizzato per il pre dimensionamento è stato calcolato considerando il carico allo stato limite ultimo moltiplicato per l’area di influenza del pilastro, a questo è stato aggiunto il peso proprio delle travi in calcestruzzo, il tutto moltiplicato per il numero di piani.
Dopo aver calcolato la tensione massima dovuta allo sforzo di compressione, abbiamo verificato che essa non superasse il valore della resistenza di calcolo a compressione del calcestruzzo scelto (C40/32)
N/A + M_t/W_max < di f_cd

Travi
Modello: trave doppiamente appoggiata
Per il pre dimensionamento degli elementi strutturali orizzontali abbiamo ipotizzato, sulla base delle precedenti esercitazioni effettuate su SAP, in aula e in autonomia, una dimensione delle travi compatibile con i carichi agenti sull’edificio, differenziando secondo le diverse tassonomie precedentemente elencate.
Il valore del momento flessionale considerato per il pre dimensionamento equivale al valore del momento massimo in campata per un modello di trave doppiamente appoggiata sottoposta a carico orizzontale linearmente distribuito, tale valore equivale a ql²/8.
Abbiamo poi definito le resistenze dei materiali: C32/40 per il calcestruzzo e acciaio S450 per le armature.
A questo punto, grazie alla teoria della flessione della trave, abbiamo potuto determinare i valori di β ed r.
Una volta determinati questi valori, abbiamo stabilito arbitrariamente una dimensione della base in modo tale da poter determinare l’altezza utile h_u e di conseguenza l’altezza totale H minima della trave in calcestruzzo.
Aggiungendo poi, oltre ai carichi precedentemente considerati, anche il peso proprio della trave stessa, e ripetendo i calcoli, abbiamo potuto ottenere il valore reale dell’altezza minima H: questo valore ci è servito per verificare le dimensioni delle sezioni da noi precedentemente ipotizzate.

Mensole
Modello: mensola orizzontale
Per il pre dimensionamento delle mensole abbiamo effettuato lo stesso procedimento precedentemente utilizzato per il pre dimensionamento delle travi.
La sola differenza sta nella scelta del valore di calcolo del momento flessionale che, in questo caso, equivale al valore del momento massimo (in corrispondenza del vincolo di incastro) di una trave che presenta una estremità incastrata a un’altra estremità libera, sottoposta al medesimo carico orizzontale linearmente distribuito. Tale valore equivale a ql²/2.

Una volta verificate tutte le sezioni ipotizzate abbiamo quindi definito su SAP le dimensioni delle sezioni per ogni tipologia di elemento strutturale:

Dimensioni degli elementi che compongono il telaio
Pilastro piano terra = 32x44 cm 
Pilastro primo piano = 30x42 cm 
Pilastro secondo piano = 28x40 cm 
Travi principali = 60x30 cm 
Travi secondarie = 35x25 cm 
Mensole = 50x30 cm 

Dimensioni degli elementi che compongono la scala
Trave a ginocchio = 30x20 cm 
Cordolo = 45x30 cm 
Montanti = 30x30 cm 

 

Modellazione in SAP2000
Per la modellazione dell’edificio su SAP abbiamo seguito le seguenti fasi:

- Per prima cosa abbiamo modellato la geometria dell’edificio su SAP grazie alla griglia e gli strumenti di disegno “Frame” e “Special Joint” ;

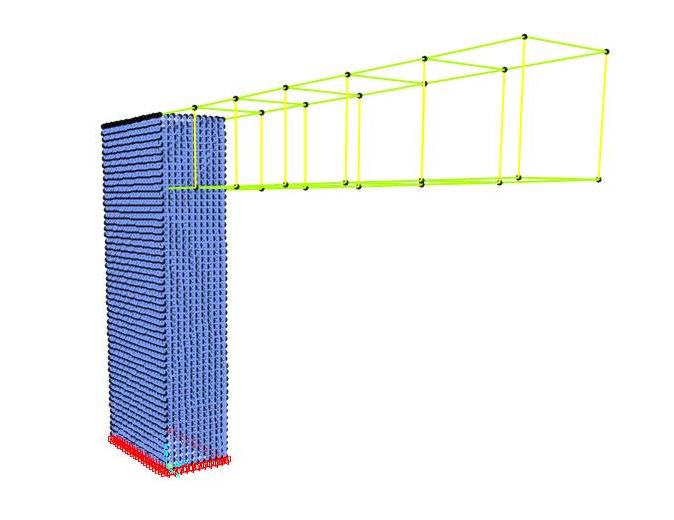
- Abbiamo poi assegnato i vincoli esterni di tipo incastro alla base dei pilastri del piano terra;

- Per simulare un nodo rigido interno, abbiamo definito i rilasci agli estremi delle aste (non abbiamo assegnato nessun rilascio alle estremità, in questo modo la rotazione intorno a tutti gli assi nel punto di collegamento tra gli elementi è pari a zero);

- Per facilitare la successiva assegnazione dei carichi, abbiamo suddiviso i vari elementi del modello in diversi gruppi:

Pilastri 0 _ Angolari
Pilastri 0 _ Perimetrali
Pilastri 0 _ Centrali
Pilastri 1 _ Angolari
Pilastri 1 _ Perimetrali
Pilastri 1 _ Centrali
Pilastri 2 _ Angolari
Pilastri 2 _ Perimetrali
Pilastri 2 _ Centrali
Travi principali _ Perimetrali
Travi principali _ Centrali
Travi secondarie _ Perimetrali
Travi secondarie _ Centrali
Corpo scala

 

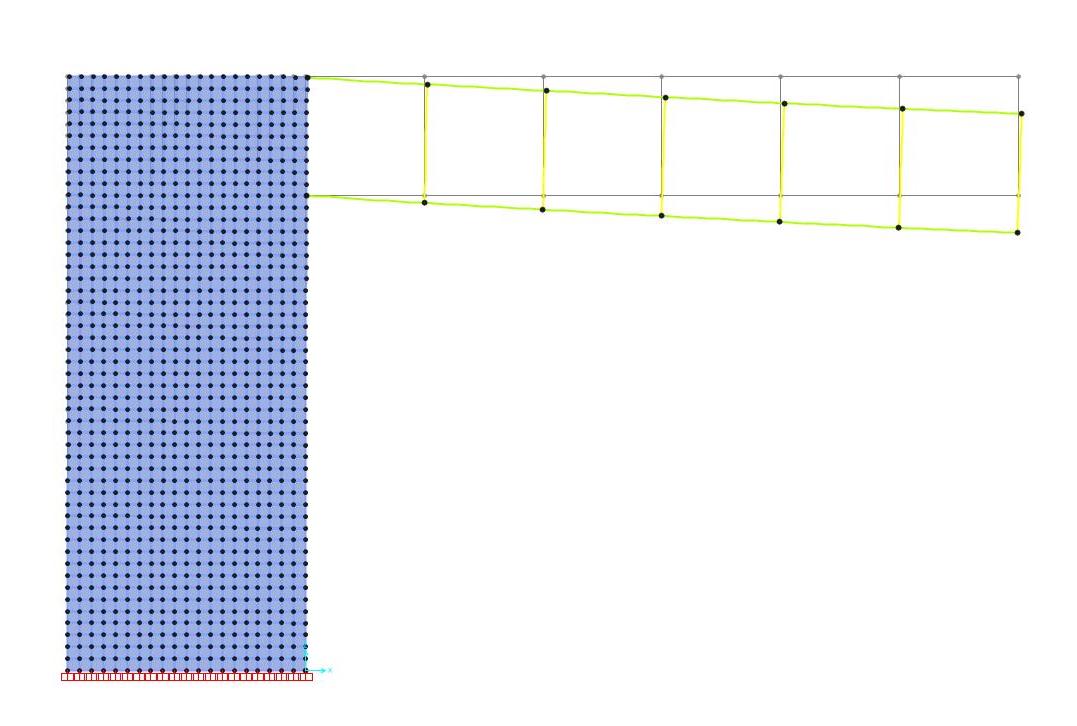
- Grazie a tale suddivisione abbiamo assegnato agli elementi strutturali le sezioni precedentemente definite;

- Successivamente abbiamo definito i carichi fissando il relativo fattore moltiplicatore del peso proprio “Load Patterns”, in questo modo abbiamo potuto considerare il peso proprio di ogni singolo elemento che compone il modello grazie al carico PP:

Qs (0)
Qp (0)
Qa (0)
PP (1)
Vento X (0)
Vento Y (0)

- Abbiamo poi definito le diverse combinazioni di carico “Load Combination” moltiplicando ogni singolo carico per il relativo coefficiente parziale di sicurezza:

- Combinazione allo stato limite ultimo: SLU
   Qs (1,3)
   Qp (1,5)
   Qa (1,5)
   PP (1,3)
- Combinazione: Vento lungo la direzione X
   SLU (1)
   Vento X (1)
- Combinazione: Vento lungo la direzione Y
   SLU (1)
   Vento Y (1)

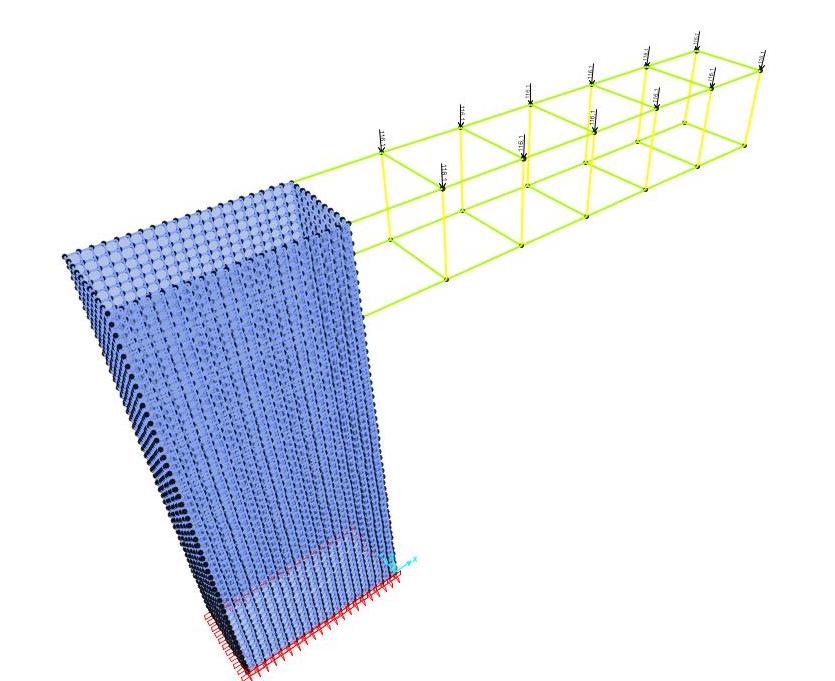
- Dopo aver definito i carichi, abbiamo assegnato a ogni elemento strutturale i rispettivi valori del carico distribuito ottenuti dall’analisi dei carichi precedentemente svolta;

- Per simulare una struttura a telaio con impalcato rigido, abbiamo assegnato il vincolo “Diaphram” dalla voce “Costrains” per tutti gli elementi orizzontali presenti per ogni piano.
In questo modo, sotto l'effetto delle forze agenti, l'impalcato si comporterà come un corpo rigido;

- Avendo scelto delle sezioni rettangolari per gli elementi verticali, abbiamo orientato i singoli pilastri con l'asse d'inerzia maggiore lungo la direzione di maggiore sollecitazione per garantire una deformazione contenuta;

 

 

 

 

- A questo punto abbiamo avviato l’analisi del modello “Run Analysis”;

- Abbiamo visualizzato la configurazione deformata della struttura, in particolare gli spostamenti verticali in corrispondenza degli aggetti, e i diagrammi delle sollecitazioni agenti (N, T, M);

- In fine abbiamo esportato le tabelle Excel relative ai valori delle sollecitazioni nella combinazione di carico allo stato limite ultimo per la verifica degli elementi inflessi e pressoinflessi.

Verifica

Verifica delle aste orizzontali
Abbiamo sostituito i valori esportati dal modello nella tabella Excel relativa alla verifica delle travi principali, secondarie e delle mensole orizzontali e abbiamo controllato che la verifica fosse soddisfatta per ogni elemento.

Travi principali

Travi secondarie

Mensole

Verifica delle aste verticali

Abbiamo creato un altro file Excel in cui abbiamo calcolato l'eccentricità dello sforzo assiale agente sui pilastri, abbiamo suddiviso questi ultimi nei vari piani inserendo le tre categorie di eccentricità, piccola moderata e grande.
Abbiamo poi verificato di quanto lo sforzo assiale fosse decentrato rispetto all'asse baricentrico dell'asta, ripetendo questa considerazione per ogni piano.
Al piano terra l'eccentricità risulta piccola in quanto i pilastri sono maggiormente soggetti a sforzo normale di compressione; al primo piano si presentano i primi pilastri con eccentricità moderata mentre all'ultimo piano i  pilastri presentano anche valori di grande eccentricità.

L'aumento della dimensione dell'eccentricità, che è definita come rapporto tra il momento intorno all'asse x e lo sforzo normale, spiega la morfologia degli elementi verticali, data l'entità degli sforzi a cui essi sono sottoposti.

Pilastri

Eccentricità

Modello 3D