In questa quinta esercitazione dobbiamo calcolare la spartizione di una forza orizzontale (forza sismica o del vento) sui diversi telai che compongono la struttura che ho preso in esame, applicando il metodo delle rigidezze.
Come modello di studio prendo in esame un generico edificio con struttura in telai shear-type in cemento armato, che riesce a svolgere il ruolo di controvento oltre che trasmettere i carichi verticali a terra.
PRIMO STEP
Per prima cosa prendiamo in esame la pianta di carpenteria dell'edificio e andiamo ad individuare i telai orizzontali e verticali. Nel mio caso individuo un totale di 14 telai, divisi in:
-7 telai verticali
-7 telai orizzontali
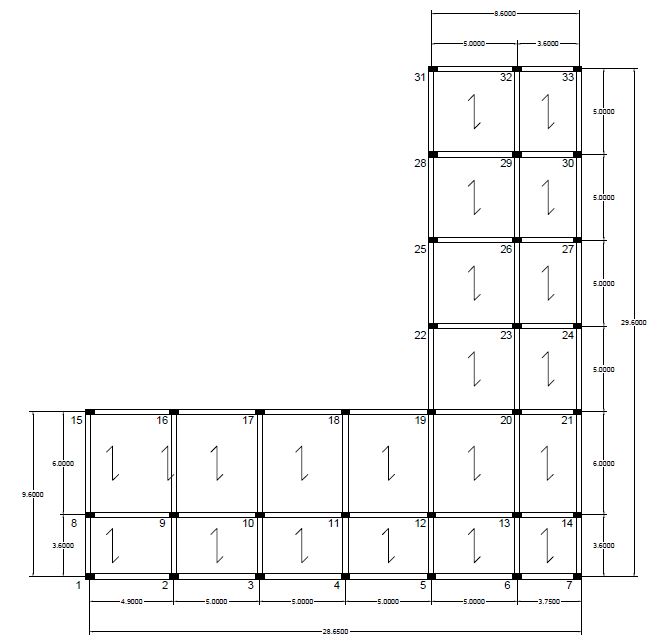
I pilastri hanno sezione 30 cm x 50 cm. Divido i telai in:
v1 = pilastri 1,8,15 o1 = pilastri 1,2,3,4,5,6,7
v2 = pilastri 2,9,16 o2 = pilastri 8,9,10,11,12,13,14
v3 = pilastri 3,10,17 o3 = pilastri 15,16,17,18,19,20,21
v4 = pilastri 4,11,18 o4 = pilastri 22,23,24
v5 = pilastri 5,12,19,22,25,28,31 o5 = pilastri 25,26,27
v6 = pilastri 6,13,20,23,26,29,32 o6 = pilastri 28,29,30
v7 = pilastri 7,14,21,24,27,30,33 o7 = pilastri 31,32,33
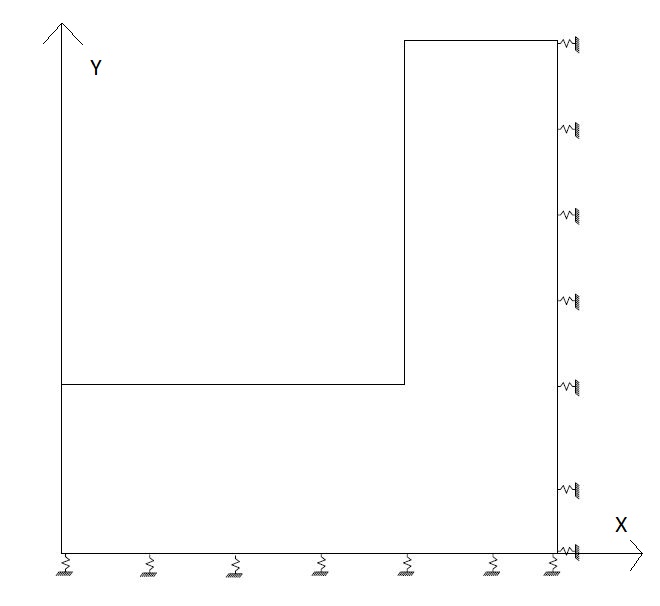
Indico nella struttura i controventi, rappresentandoli in pianta come delle molle. Sono un particolare tipo di vincolo che esercitano una forza reattiva ma allo stesso tempo subiscono una deformazione, tra la forza reattiva e la deformazione vi è una diretta proporzione.
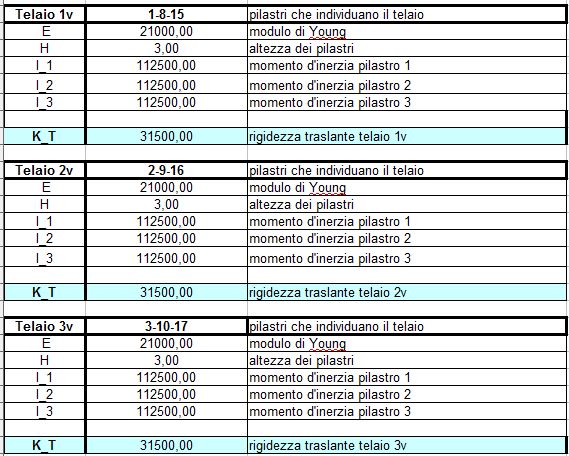
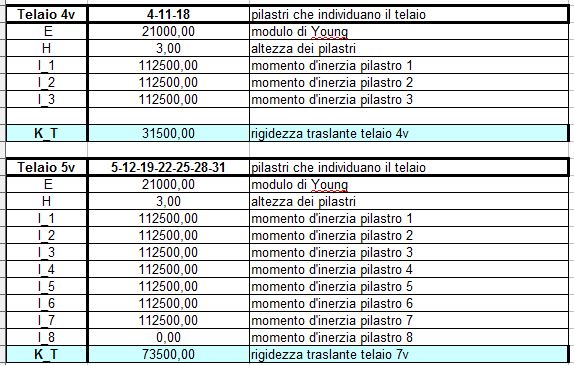
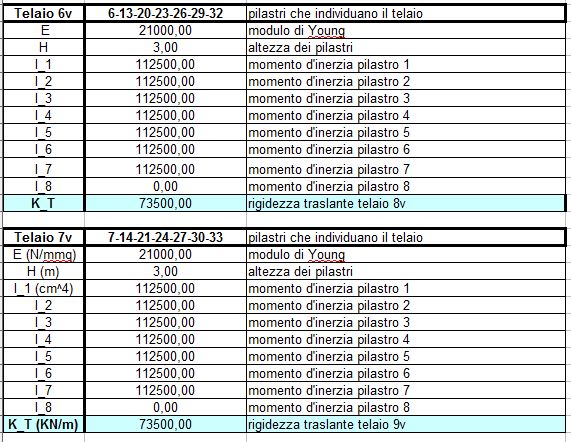
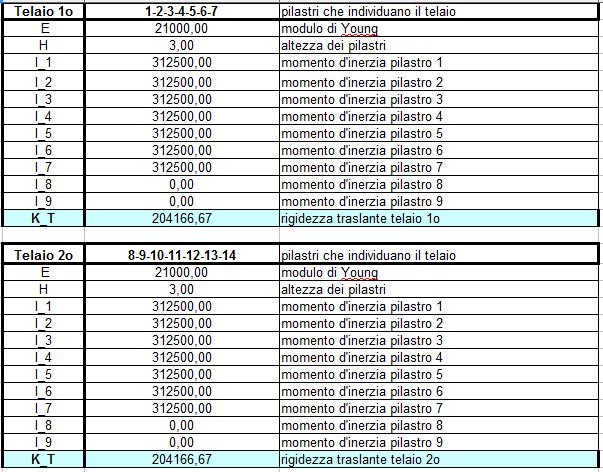
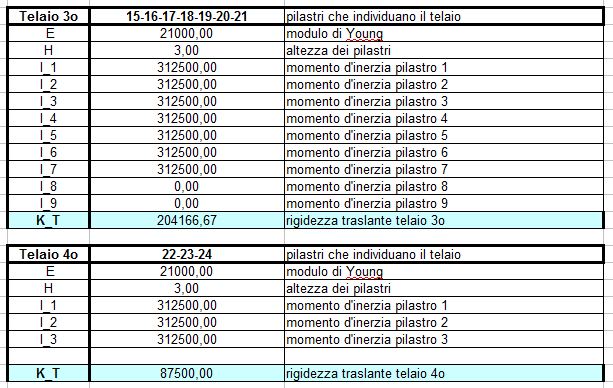
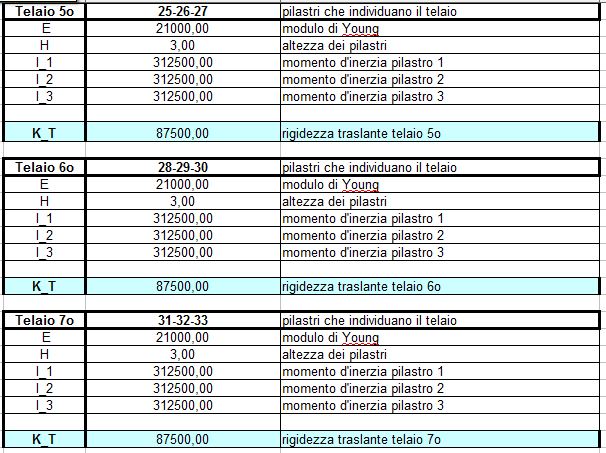
In questo primo step mi devo ricavarela rigidezza traslante di ogni telaio (k = 12 EI/ h3 + 12 EI/ h3). Bisogna stare attenti al diverso orientamento dei pilastri poichè questi offrono un momento d’inerzia diverso in base al loro orientamento (bh^3/12).
I due valori possibili sono 112500.00 cm4 e 312500.00 cm4.
SECONDO STEP
Nella seconda tabella sono riportate le rigidezza dei controventi analizzati precedentementi, e la distanza di ciascuno di essi dall'origine.
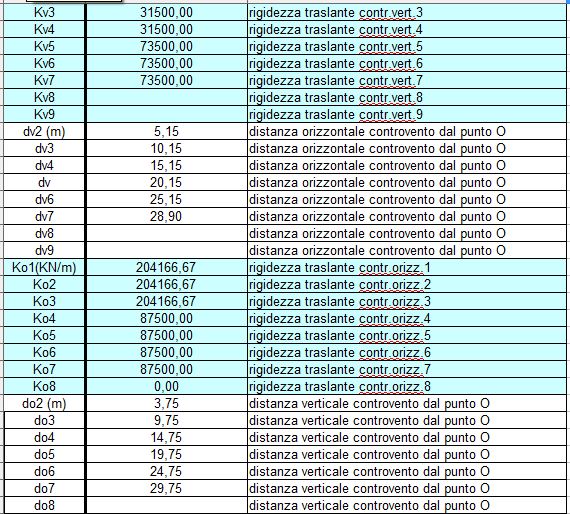
TERZO E QUARTO STEP
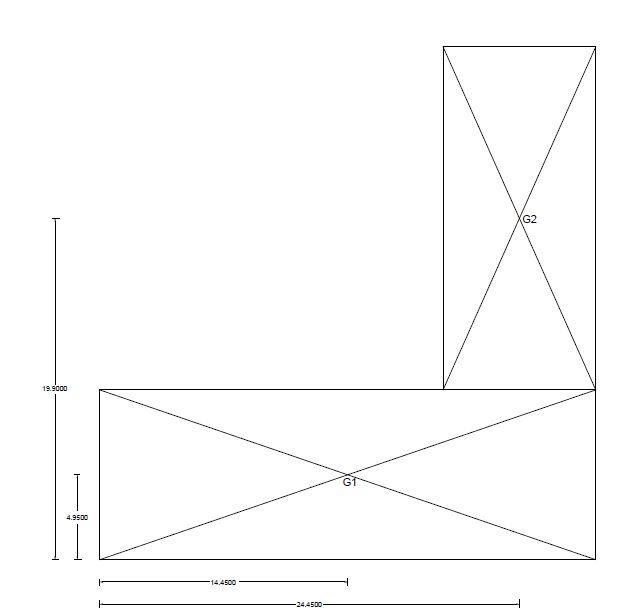
In questo passo dobbiamo calcolare il centro di massa dell'impalcato. Per semplificare questo calcolo, divido la forma della mia pianta in figure geometricamente semplici ( la L dell'edificio viene divisa in due rettangoli). Misuro l’area di questi e la distanza dei loro centri d’area con l’origine fissata precedentemente.
Con questi dati applico la formula per ottenere le due coordinate del centro di massa dell'impalcato:
Xg= A1*Xg1 + A2*Xg2 + A3*Xg3 / Atot
Yg= A1*Yg1 + A2*Yg2 + A3*Yg3 / Atot
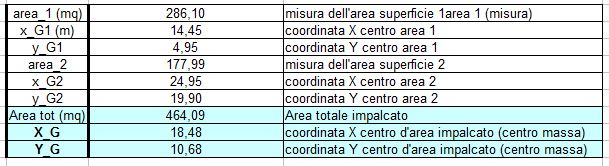
Il mio centro di massa G ha come cordinate ( XG =18,48; YG= 10,68). A questo punto vado a sostituire nella formula del centro di massa, la rigidezza dei telai al posto delle aree e la loro distanza dall'origine degli assi, al posto di xG1, xG2, yG1 e yG2. E' possibile ora trovare le coordinate del centro delle rigidezze C dell'impalcato.
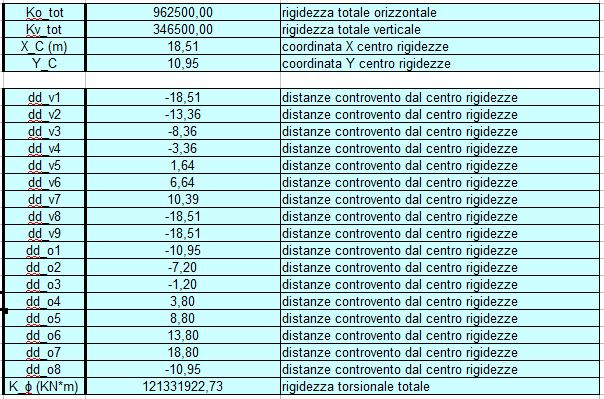
Il centro delle rigidezze ha come coordinate Xc= 18.51 m; Yc= 10.95 m. In questo caso il centro di massa e il centro delle rigidezze si trovano molto vicini. Ciò implica che l’impalcato colpito da una forza lungo X o da una forza lungo Y subirà semplicemente una traslazione, senza subire una rotazione. Invece se i due punti fossero capitati molto più distanti, questa distanza sarebbe servita come "braccio" del momento, sia in caso di una forza orizzontale, che nel caso di una forza verticale.
QUINTO STEP
Nella quinta tabella utilizziamo l'analisi dei carichi sismici per ricavare il valore della forza sismica complessiva agente sul centro di massa. A questo punto vado a riprendere i valori di qs, qp e qa che ho ottenuto nella prima esercitazione, mentre la destinazione ad uso residenzia dell'edificio mi determina un coefficiente di contemporaneità di ψ = 0,3.
Il coefficiente di intensità sismica c viene determinato dall'area geografica dell'impalcato ed è pari a c = 0,10.
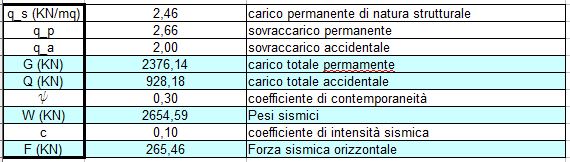
F = 130, 32 KN è il valore della forza sismica da applicare in entrambe le direzioni (x;y)
SESTO E SETTIMO STEP
Negli ultimi due step le tabelle determinano la ripartizione della forza sismica sui vari telai e gli effetti che va a provocare sul telaio.
Nello specifico la sesta tabella prende in esame la traslazione e la rotazione scaturite da Fx, mentre la successiva analizza gli stessi effetti legati a Fy
Ripartizione forza sismica lungo X
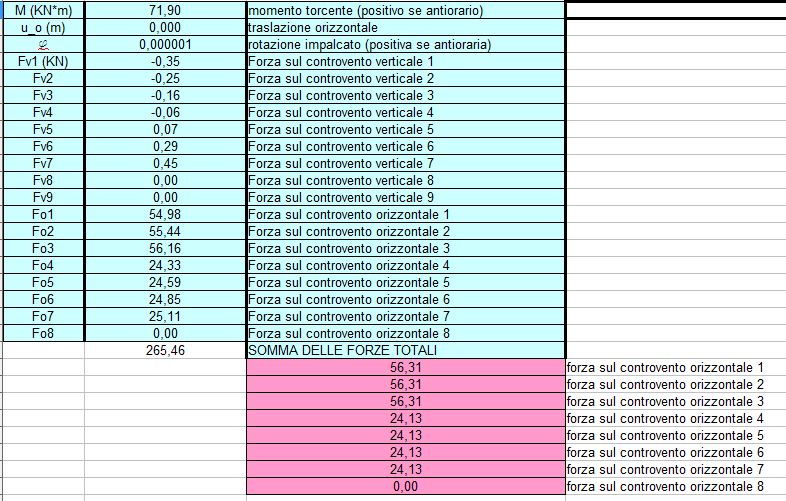
Ripartizione forza sismica lungo Y
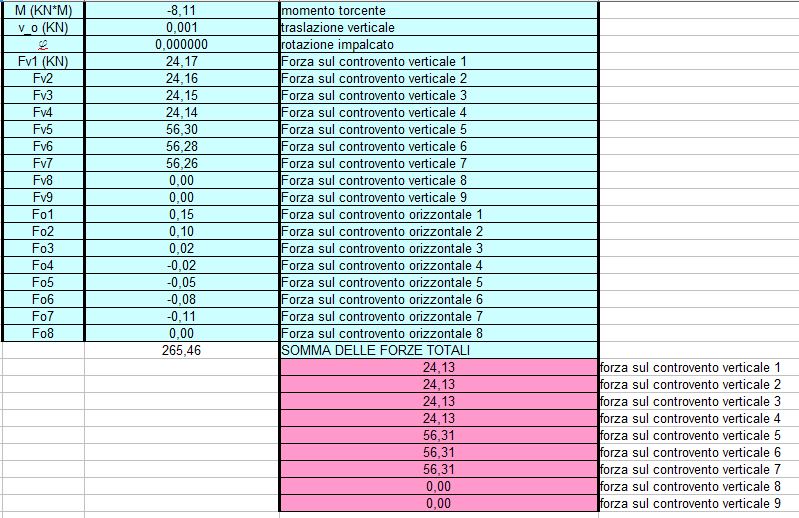
Gli effetti dell'azione sismica legati a Fx sono i seguenti:
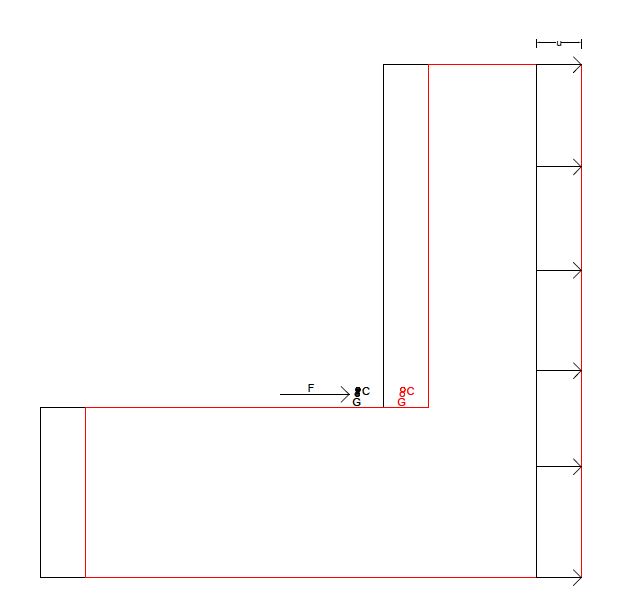
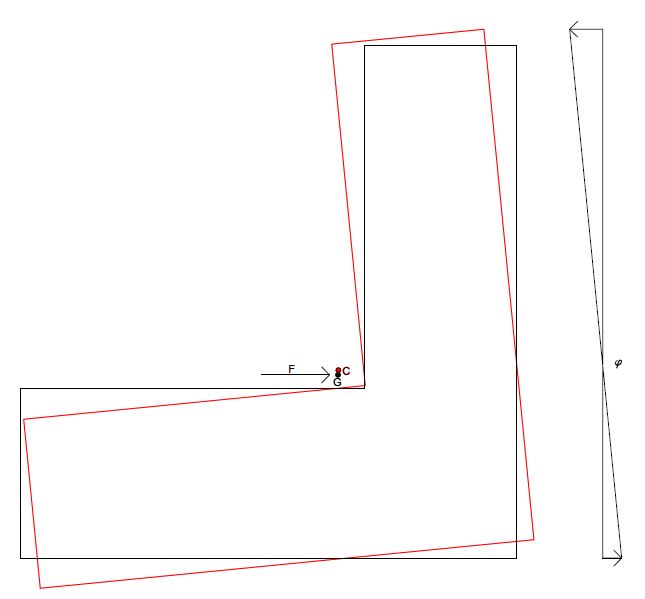
Gli effetti dell'azione sismica legati a Fy sono i seguenti:
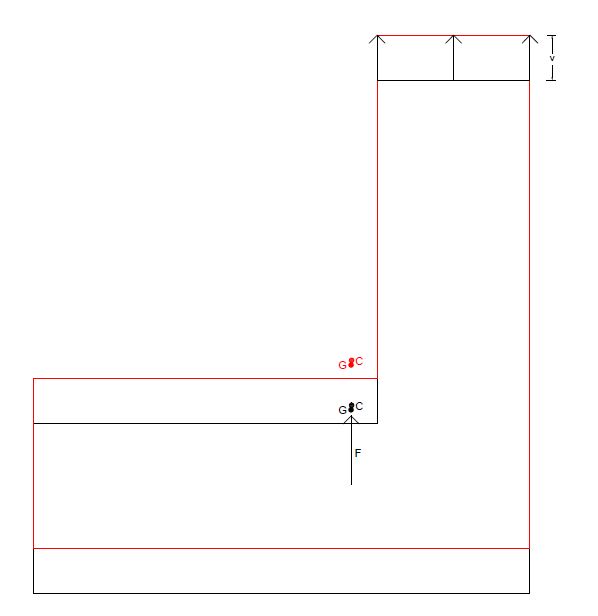
Commenti recenti