Portale di Meccanica

Questa esercitazione consiste nel dimensionamento del pilastro più sollecitato in un telaio nelle tre diverse tecnologie: legno, acciaio e cemento armato.

L1 = 7m

L2 = 5m

Area di influenza = L1 x L2 = 35m²

Numero piani = 4

 

Il pilastro sottoposto a maggiore sforzo normale nella struttura presa in analisi è quello evidenziato in rosso: su di esso infatti grava il carico di travi e solaio per la maggiore area di influenza che dovrà essere moltiplicato per il numero dei piani sovrastanti.

LEGNO

 

Contributo delle travi

Si calcola moltiplicando il peso unitario di ciascuna trave (considero il peso unitario della trave calcolato nella prima esercitazione) per l’interasse, moltiplicando il valore ottenuto per il coefficiente di sicurezza per carichi strutturali pari a 1.3.

 

Qtravi = (Peso unitario trave1 x  L1 x 1.3) + (Peso unitario trave2 x L2 x 1.3)

 

Contributo del solaio

Si ottiene moltiplicando la somma dei carichi (strutturali, permanenti e accidentali calcolati nella prima esercitazione e maggiorati dei rispettivi coefficienti di sicurezza) per l’area di influenza.

 

Qsolaio = [(qs x1.3) + (qp x 1.5) + (qa x 1.5)] x area di influenza

 

È dunque possibile calcolare lo sforzo normale agente sul pilastro del piano terra

N = (Qtravi + Qsolaio) x 4 piani

 

Un pilastro sottoposto a compressione può essere soggetto a rottura per schiacciamento del materiale o soggetto all’innesco del fenomeno di instabilità.

 

Per evitare il fenomeno di rottura per schiacciamento la tensione massima nel pilastro (σmax) deve essere minore della resistenza a compressione di progetto del materiale (fcd).

 

σmax < fcd

 

Imponendo σmax = fcd possiamo ricavare l’area minima della sezione ovvero il valore minimo che deve avere l’area per non essere soggetta a rottura.

Infatti poiché

σmax = N/Amin

fcd = N/Amin

 

In fase progettuale si è scelto per il pilastro un legno lamellare GL24h con resistenza caratteristica fmk pari a 24 Mpa. La resistenza di progetto fd che viene calcolata dal foglio tiene conto della resistenza caratteristica corretta con alcuni parametri:

fd = (kmod x fmk)/γm

γm è un coefficiente di sicurezza del materiale: in questo caso per il legno lamellare γm = 1.45.

Kmod è un coefficiente correttivo che tiene conto della durata di carico (consideriamo una durata media) e dell’umidità della struttura (consideriamo una classe media).

 

dunque ora, conoscendo il valore di fcd, è possibile calcolare l’area minima con la formula inversa.

Amin =N/fcd

 

Affinché, invece, nel pilastro non si inneschi un fenomeno di instabilità lo sforzo nomale deve essere inferiore allo sforzo critico euleriano.

 

N<Ncrit

 

Sappiamo che

Ncrit= (π²EImin)/(βl)²

 

Poiché

βl = l0 (lunghezza libera di inflessione)

Imin=Aρmin²

 

Ncrit = (π²EAρmin²)/(l0)²

 

Poiché λ=l0/ρmin

Ncrit = π²EA/ λ²

 

Allo sforzo critico euleriano è possibile associale una tensione critica

σcrit = Ncrit/A = π²E/ λ²

 

Per evitare il fenomeno di instabilità la tensione massima nel pilastro (σmax) deve essere minore della tensione critica (σcrit)

σmax < σcrit

 

Poiché abbiamo imposto

σmax = fcd

allora

 

fcd < σcrit    (prima di inflettersi per instabilità, il pilastro si rompe. Questa soluzione è

                       ottimale poiché l’instabilità non è controllabile)

fcd < π²E/ λ²

λ² < π²E/fcd

λmax = π √(E/fcd)

Dunque una volta inseriti i valori del modulo di elasticità (E) proprio del materiale e la resistenza di progetto (fcd), il foglio di calcolo ricava la snellezza massima del pilastro (λmax).

Ma, poiché

λ = l0/ρmin

 

ρmin = l0/λ

 

Dunque una vola inseriti i valori di β e della lunghezza del pilastro (l), si ottiene il valore della lunghezza libera di inflessione (l0) che il foglio di calcolo dividerà per la snellezza massima appena ricavata: dunque si ottiene il raggio di inerzia minimo. Ricordando che nelle sezioni rettangolari

ρmin = √(1/12) b

possiamo ricavare la base tramite la formula inversa:

bmin = 2√3 ρmin

Una volta ingegnerizzata calcoliamo l’altezza minima

hmin= Amin/b

Una volta ingegnerizzata anche l’altezza il foglio ricalcola l’area e il momento d’inerzia di design. Dunque sarà necessario verificare che l’area di design sia maggiore dell’area minima precedentemente calcolata.

 

ACCIAIO

Per calcolare lo sforzo normale agente sul pilastro si sommano nuovamente i contributi di travi e solaio all’interno dell’area di influenza e si moltiplicano per il numero di piani.

Anche in questo caso, per ricavare il contributo delle travi, si sceglie il peso unitario delle travi della prima esercitazione e si moltiplica per l’interasse relativo e per il coefficiente si sicurezza strutturale.

Qtravi = (Peso unitario trave1 x  L1 x 1.3) + (Peso unitario trave2 x L2 x 1.3)

 

Poi per ricavare il contributo del solaio si scelgono i valori dei carichi strutturali, permanenti e accidentali della prima esercitazione, si maggiorano con i relativi coefficienti di sicurezza e la loro somma viene moltiplicata per l’area di influenza.

Qsolaio = [(qs x1.3) + (qp x 1.5) + (qa x 1.5)] x area di influenza

 

È dunque ora possibile calcolare lo sforzo normale agente sul pilastro del piano terra

N = (Qtravi + Qsolaio) x 4 piani

 

Avendo scelto per la trave un acciaio S275 con resistenza caratteristica fyk=275Mpa, si ricava la resistenza di progetto correggendo quella caratteristica con un coefficiente di sicurezza γm=1.05.

fyd = fyk/γm

Dunque imponendo σmax = fyd possiamo ricavare l’area minima della sezione come sopra:

 

Amin= N/fyd

 

Come per il legno inserendo i dati relativi al modulo di elasticità (E) relativo al materiale e la resistenza di progetto (fyd) appena calcolata, il foglio ricava il valore della snellezza massima

λmax = π √(E/fcd)

Inserendo poi i valori di β e della lunghezza del pilastro (l), si ottiene il valore della lunghezza libera di inflessione (l0) che il foglio di calcolo dividerà per la snellezza massima appena ricavata: dunque si ottiene il raggio di inerzia minimo.

ρmin = l0/λ

 

Ora, poiché la sezione di un pilastro in acciaio non è rettangolare, bensì sarà un profilo HEA possiamo calcolare il momento di inerzia minimo con la formula

Imin = A x ρmin²

Ora sarà possibile scegliere su un sagomario l’HEA che possiederà un momento inerzia, un raggio di inerzia e un area immediatamente superiori a quelle trovate. Il foglio ricalcolerà la snellezza con i nuovi valori e si dovrà verificare che non superi il valore 200.

 

CEMENTO ARMATO

Per calcolare lo sforzo normale agente sul pilastro si sommano nuovamente i contributi di travi e solaio all’interno dell’area di influenza e si moltiplicano per il numero di piani.

Anche in questo caso, per ricavare il contributo delle travi, si sceglie il peso unitario delle travi della prima esercitazione e si moltiplica per l’interasse relativo e per il coefficiente si sicurezza strutturale.

Qtravi = (Peso unitario trave1 x  L1 x 1.3) + (Peso unitario trave2 x L2 x 1.3)

 

Poi per ricavare il contributo del solaio si scelgono i valori dei carichi strutturali, permanenti e accidentali della prima esercitazione, si maggiorano con i relativi coefficienti di sicurezza e la loro somma viene moltiplicata per l’area di influenza.

Qsolaio = [(qs x1.3) + (qp x 1.5) + (qa x 1.5)] x area di influenza

 

È dunque ora possibile calcolare lo sforzo normale agente sul pilastro del piano terra

N = (Qtravi + Qsolaio) x 4 piani

 

Scelgo poi un calcestruzzo classe C60/75 con resistenza caratteristica fck = 60 Mpa.

Il foglio di calcolo ricava la resistenza di progetto con la formula

Fcd= (α x fck)/ γm

Dove γm è il coefficiente di sicurezza di 1.5

e α è un coefficiente che tiene conto del tempo pari a 0.85

 

Dunque imponendo σmax = fcd possiamo ricavare l’area minima della sezione come sopra:

 

Amin= N/fcd

 

Come per il caso di legno e acciaio inserendo i dati relativi al modulo di elasticità (E) relativo al materiale e la resistenza di progetto (fyd) appena calcolata, il foglio ricava il valore della snellezza massima

λmax = π √(E/fcd)

Inserendo poi i valori di β e della lunghezza del pilastro (l), si ottiene il valore della lunghezza libera di inflessione (l0) che il foglio di calcolo dividerà per la snellezza massima appena ricavata: dunque si ottiene il raggio di inerzia minimo.

ρmin = l0/λ

 

Come nel caso del legno possiamo ricavare la base tramite la formula:

bmin = 2√3 ρmin

Una volta ingegnerizzata calcoliamo l’altezza minima

hmin= Amin/b

Una volta ingegnerizzata anche l’altezza, il foglio ricalcola l’area e il momento d’inerzia di design.

 

Per il pilastro in calcestruzzo è necessario aggiungere un ulteriore verifica. Infatti il pilastro non sarà soggetto a sola compressione, ma anche a flessione derivante dall’incastro che avremo nel nodo trave pilastro. Dunque per verificare a presso-flessione dovremo controllare che la tensione massima dovuta sia allo sforzo normale che al momento flettente sia inferiore alla tensione di progetto.

σmax = N/A + Mt/Wmax < fcd

Dunque il foglio, avendo tutti i dati, calcola automaticamente il modulo di resistenza a flessione Wmax

Wmax= bh²/6

E il momento all’estremo della trave e quindi sulla testa del pilastro che viene calcolato come

Mt= (qt x Lp²)/12

Dove qt (calcolato da foglio) è il carico di solaio distribuito sulla trave principale: quindi si sommano i carichi strutturali, permanenti e accidentali maggiorati per l’interasse tra le travi principali ovvero qt = [(qs x 1.3) + (qp x 1.5) + (qa x 1.5)] x Ls.

Dunque il foglio di calcolo ricava il σmax e verifica se risulta minore di fcd. Se non risulta verificato sarà necessario aumentare gradualmente le dimensioni del pilastro fino alla verifica di questa condizione.

 

 

 

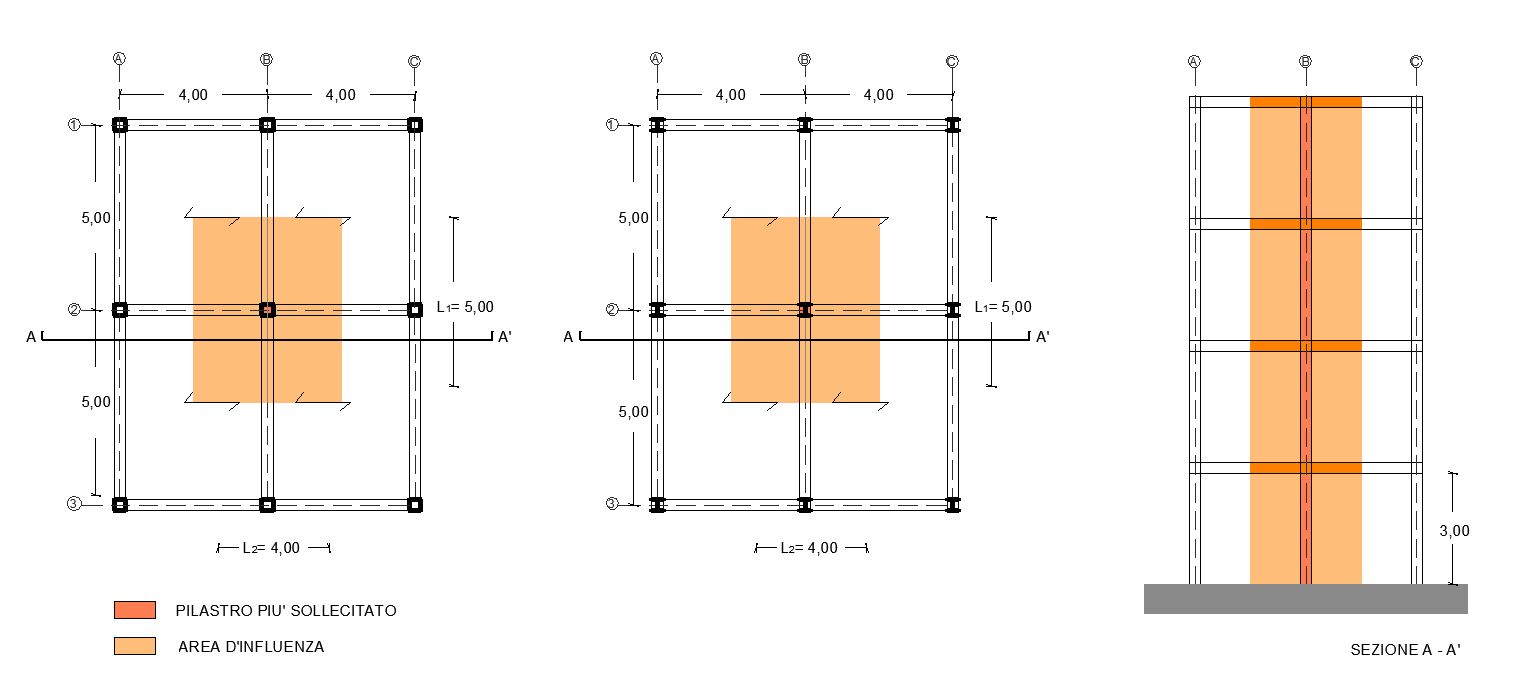
Lo scopo di questa esercitazione è il dimensionamento di un pilastro nelle tre diverse tecnologie: Legno, Acciio e Calcestruzzo armato.

Osservando le piante, appare subito evidente che il pilastro più sollecitato risulti essere quello centrale, perchè quello con area di influenza maggiore A = L₁ x L₂ = m 5,00 x 4,00 = 20 m².

Poichè il foglio di calcolo necessita di alcune informazioni relative ai carichi che gravano sui solai, faranno riferimento la prima e la terza esercitazione EXE1_Dimensionamento di una trave per un solaio in legno, acciaio e calcestruzzo armato e EXE3_Verifica a deformabilità di una trave a sbalzo.

 

LEGNO

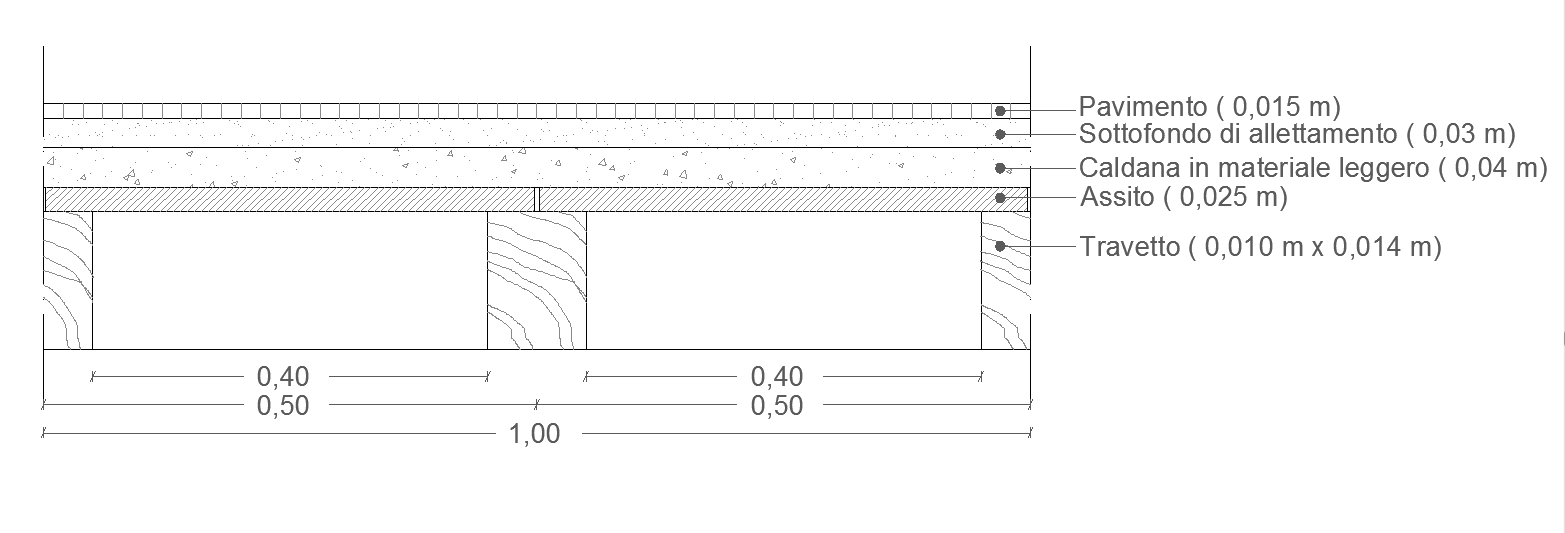
La prima parte del foglio Excel è impostata sul calcolo dello sforzo normale di compressione N agente sul pilastro.

Per definire questo valore è necessario prima di tutto individuare il carico dovuto al peso proprio delle travi, moltiplicando l'area della sezione della trave per il peso specifico del materiale di cui quest'ultima è composta.

Area sezione = (0,30 x 0,55) m

Peso specifico = 8 KN/m³

Di conseguenza:

Trave_p = (0,30 x 0,55) m x 8 KN/m^{3 =} 1,32 KN/m

Trave_s = (0,30 x 0,55) m x 8 KN/m^{3 =} ​1,32 KN/m

Si inseriscono a questo punto i valori dei carichi gravanti sul solaio e il numero dei piani n = 4

Carico strutturale (Qs) = 0,265 KN/m²

Carico permanente (Qp) = 2,66 KN/m²

Carico accidentale (Qa) = 2,00 KN/m²

La successiva parte del foglio di calcolo prevede di definire l'area minima A_min che la sezione del pilastro deve avere per evitare che il materiale entri in crisi. Per ottenere ciò, devo essere inseriti alcuni parametri:

- La resistenza a flessione caratteristica con fibre di legno parallele f_c0,k = 21 MPa;

- Il coefficiente di durata del carico k_mod = 0,8;

- Il coefficiente parziale di sicurezza del materiale γ_m = 1,45

 La terza parte del foglio di calcolo è incentrata sulla definizione della base b e dell'altezza h.

Per fare ciò bisogna inserire ancora alcuni dati:

- Il modulo di elasticità del materiale E = 8.800 N/mm²;

- Il coefficiente adimensionale che riflette l’influenza dei vincoli β = 1;

- L'altezza del pilastro l = 3m.

Attraverso l'utilizzo di questi parametri si riesce a calcolare:

- Il valore massimo della snellezza λ_max;

- Il vaolre minimo del raggio d'inerzia ρ_min.

Ora è possibile calcolare una delle due dimensioni della sezione del pilastro, ossia la base minima b_min. Questo valore dovrà però essere ingegnerizzato, dovrà cioè essere scelto un valore della base b superiore ad b_min. A questo punto, nota una delle due dimensioni, potrà essere definita anche l'altra, l'altezza h_min, che andrà a sua volta ingegnerizzata, per ottenere un valore h_min < h.

L'ultima operazione consiste nella fase di verifica. 

Infatti, dopo aver definito i valori di base e altezza della sezione del pilastro, con b < h, il foglio Excel individuerà anche l'area di progetto A_design. La sezione risulterà verificata se, e solo se, A_design > A_min

700 cm² > 529 cm²

LA SEZIONE E' VERIFICATA!

 

ACCIAIO

 

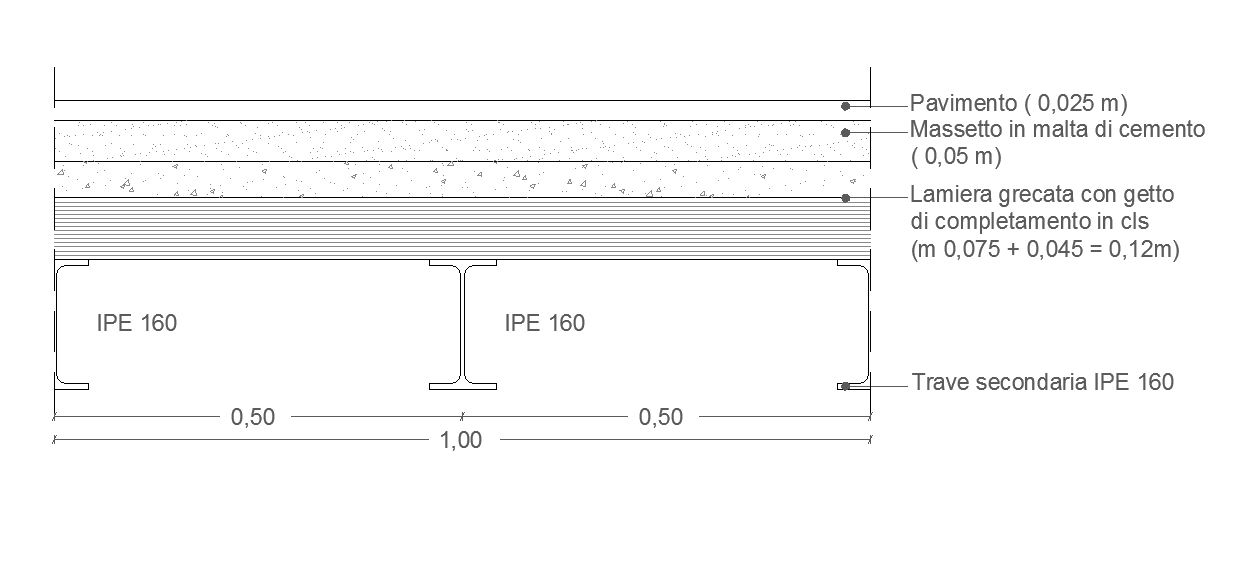
Come nel caso del legno, anche per il dimensionamento di un pilastro in acciaio, la prima parte del foglio Excel è impostata sul calcolo dello sforzo normale di compressione N agente sul pilastro.

Per definire questo valore è necessario prima di tutto individuare il carico dovuto al peso proprio delle travi, quindi:

Trave_p (IPE 400) = 66,3 Kg/m = 0,66 KN/m

Trave_s (IPE 160) = 15,8 Kg/m = 0,16 KN/m

Si inseriscono a questo punto i valori dei carichi gravanti sul solaio e il numero dei piani n = 4

Carico strutturale (Qs) = 2,03 KN/m²

Carico permanente (Qp) = 2,95 KN/m²

Carico accidentale (Qa) = 2,00 KN/m²

La successiva parte del foglio di calcolo prevede di definire l'area minima A_min che la sezione del pilastro deve avere per evitare che il materiale entri in crisi. Per ottenere ciò, devo essere inseriti alcuni parametri:

- La tensione di snervamento f_yk = 275 MPa;

- Il coefficiente parziale di sicurezza del materiale γ_m = 1,05

 La terza parte del foglio di calcolo è incentrata sulla definizione del momento di inerzia minimo I_min.

Per fare ciò bisogna inserire ancora alcuni dati:

- Il modulo di elasticità del materiale E = 210.000 N/mm²;

- Il coefficiente adimensionale che riflette l’influenza dei vincoli β = 1;

- L'altezza del pilastro l = 3 m.

Attraverso l'utilizzo di questi parametri si riesce a calcolare:

- Il valore massimo della snellezza λ_max;

- Il vaolre minimo del raggio d'inerzia ρ_min.

Ora è possibile calcolare il momento d'inerzia minimo I_min = A x (ρ_min)²

Attraverso l'ingegnerizzazione dei valori di ρ_min e I_min sarà possibile scegliere il profilo HEA adatto. Bisognerà dunque vedere sulla Tabella Profilati metallici, qual è quello che riporta i valori di raggio minimo di inerzia e momento di inerzia minimo superiori rispetto a quelli del foglio di calcolo.

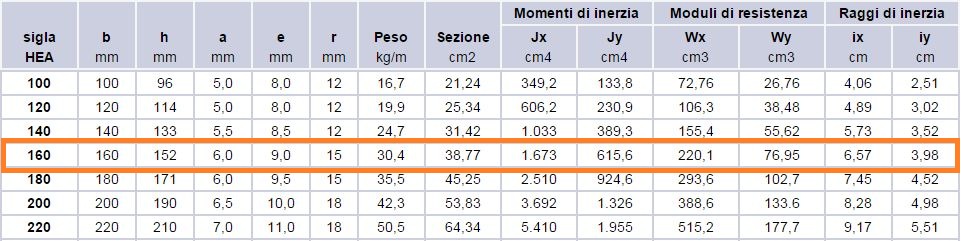
Il profilo scelto è un HEA 160. A questo punto, dopo aver inserito l'area di progetto A_design, il momento di inerzia minimo di progetto I_design e il raggio minimo d'inerzia ρ_min, il profilo risulterà verificato se, e solo se 

A_design > A_min

IL PROFILO E' VERIFICATO!

 

 

CALCESTRUZZO ARMATO

 

Come nel caso del legno e dell'acciaio, anche per il dimensionamento di un pilastro calcestruzzo armato, la prima parte del foglio Excel è impostata sul calcolo dello sforzo normale di compressione N agente sul pilastro.

Per definire questo valore è necessario prima di tutto individuare il carico dovuto al peso proprio delle travi, moltiplicando l'area della sezione della trave per il peso specifico del materiale di cui quest'ultima è composta.

Area sezione = (0,30 x 0,50) m

Peso specifico = 25 KN/m³

Di conseguenza:

Trave_p = (0,30 x 0,50) m x 25 KN/m^{3 =} 3,75 KN/m

Trave_s = (0,30 x 0,50) m x 25 KN/m^{3 =} ​3,75 KN/m

Si inseriscono a questo punto i valori dei carichi gravanti sul solaio e il numero dei piani n = 4

 

Carico strutturale (Qs) = 2,54 KN/m²

Carico permanente (Qp) = 2,35 KN/m²

Carico accidentale (Qa) = 3,00 KN/m²

La successiva parte del foglio di calcolo prevede di definire l'area minima A_min che la sezione del pilastro deve avere per evitare che il materiale entri in crisi, e di conseguenza anche la dimensione minima della base b_min. Per ottenere ciò, deve essere inserita la tensione di snervamento f_ck = 40 MPa;

La terza parte del foglio di calcolo è incentrata sulla definizione del momento di inerzia minimo I_min.

Per fare ciò bisogna inserire ancora alcuni dati:

- Il modulo di elasticità del materiale E = 21.000 N/mm²;

- Il coefficiente adimensionale che riflette l’influenza dei vincoli β = 1;

- L'altezza del pilastro l = 3 m.

Attraverso l'utilizzo di questi parametri si riesce a calcolare:

- Il valore massimo della snellezza λ_max;

- Il vaolre minimo del raggio d'inerzia ρ_min.

Dopo aver determinato una delle due dimensioni della sezione del pilastro, ossia la base minima b_min si potrà ingegnerizzare, dovrà cioè essere scelto un valore della base b superiore ad b_min. A questo punto, nota una delle due dimensioni, potrà essere definita anche l'altra, l'altezza h_min, che andrà a sua volta ingegnerizzata, per ottenere un valore h_min < h.

L'ultima operazione consiste nella fase di verifica. 

Infatti, dopo aver definito i valori di base e altezza della sezione del pilastro, con b < h, il foglio Excel individuerà anche l'area di progetto A_design. La sezione risulterà verificata se

                                                                                A_design > A_min    (1)

In questo caso però è necessaria un’ulteriore verifica della sezione, poiché nel cemento armato il nodo tra trave e pilastro, essendo realizzato con un incastro, trasmette momento, sottoponendo il pilastro a presso-flessione.

E' per questo motivo che oltre alla (1), bisogna imporre anche che

                                                                                  σ_max ≤ f_cd

Poichè tutte e due le condizioni risultano soddisfatte

LA SEZIONE E' VERIFICATA!

 

La quarta esercitazione consiste nel dimensionamento di un pilastro nelle tre varie tecnologie: legno, acciaio e calcestruzzo.

Per l’esercitazione ho preso in considerazione il pilastro maggiormente sollecitato a sforzo normale (N) di un edificio di 3 piani; uno di quelli presenti a piano terra sui quali scarica il peso dell'intera struttura sovrastante.

Ho ripreso la pianta di carpenteria utilizzata nella prima esercitazione in modo da poter riutilizzare i valori dei carichi dei solai.

L'area di influenza del pilastro è di 24 mq. (L1= 4 m ; L2= 6 m)

LEGNO

- Dopo aver inserito i dati relativi alla grandezza del solaio ed aver trovato l'area di influenza del pilastro, calcolo il peso unitario della trave_p e della trave_s

trave= area della sezione (0,30 x 0,40) mq x peso specifico 6 KN/m3 = 0,72 KN/m

 

Posso calcolare il carico dovuto al peso proprio delle travi 

q trave= (trave p x L1 x 1,3) + (trave s x L2 x 1,3) = 9,36 KN

 

- Per calcolare il valore complessivo del carico agente, inserisco i valori dei carichi agenti sul solaio: carichi strutturali, carichi permanenti e carichi accidentali

q solaio= (1,3 x qs + 1,5 x qp + 1,5 x qa) x A = 191,36 KN

 

- Per finire calcolo lo sforzo di compressione N

N= (q trave x q solaio) x n piani= 602 KN

 

 

Posso così calcolare l’ area minima necessaria affinché il materiale non entri in crisi.

- Inserisco i dati relativi al materiale:

 

la resistenza a compressione (f_c0,k) 24MPa

 

il coefficiente della durata di carico k_mod  0,8

 

il coefficiente parziale di sicurezza γ_m. 1,45

 

e ricavo il valore della tensione ammissibile e dell'area minima:

f_c0d= f_c0,k x k_mod / γ_m. = 13,24 MPa

A min= 454,8 cm2

 

 

- Sapendo che Il modulo di elasticità E = 8800 MPa, β =1 e l’altezza del pilastro è di 3 m, posso calcolare:

valore massimo di snellezza λ_{max =} 80,95

valore minimo del raggio di inerzia ρ_min = 3,71 cm

la grandezza della base minima (b min) = 12,84 cm, che ingegnerizzo a b = 15 cm. 

l’altezza minima h_min =   A_min / b = 30,32 cm, che ingegnerizzo a h = 35 cm

                                                                    

- Calcolo  l’area di progetto della sezione

A_design = b x h = 525 cm²

 

- Verifico che A_design > A_min   

 

525 cm² >  454,8 cm²               

 

SEZIONE VERIFICATA

ACCIAIO

- Dopo aver inserito i dati relativi alla grandezza del solaio ed aver trovato l'area di influenza del pilastro, calcolo il peso unitario della trave p e della trave s

 

trave p = IPE 270 = 36,1 Kg/m = 0,361 KN/m

 

trave s = IPE 120 = 10,4 Kg/m = 0,104 KN/m

 

Posso calcolarmi così il carico dovuto al peso proprio delle travi 

q trave= 2,69 KN

 

- Per calcolare il valore complessivo del carico agente, inserisco i valori dei carichi agenti sul solaio: carichi strutturali, carichi permanenti e carichi accidentali 

q solaio= (1,3 x qs + 1,5 x qp + 1,5 x qa) x A = 202,39 KN

 

- Per finire calcolo lo sforzo di compressione N

N= (q trave x q solaio) x n piani= 615 KN

 

Posso così calcolare l’ area minima necessaria affinché il materiale non entri in crisi.

- Inserisco i dati relativi al materiale:

tensione di snervamento (f_,yk) 275MPa

                                          

il coefficiente parziale di sicurezza γ_m. 1,05

 

Ricavo così il valore della tensione ammissibile e dell’area minima

 

f_yd= f_yk / γ_m = 261,90 MPa

 

A min= 23,5 cm²

 

 

- Sapendo che Il modulo di elasticità E = 210000 MPa, β =1 e l’altezza del pilastro è di 3 m, posso calcolare:

valore massimo di snellezza λ_{max =} 88,96

valore minimo del raggio di inerzia ρ_min = 3,37 cm

calcolo il momento di inerzia minimo I_{min =}  267 cm⁴

 

- rispetto ai valori ricavati posso ingegnerizzare la sezione scegliendo un profilo HEA con valori maggiori rispetto a quelli minimi trovati. Scelgo un profilo HEA 140

 

- Verifico che A_design > A_min

 

31,4 cm² > 23,5 cm²           

 

- Verifico che  λ <  λ*

 

85,23 <  88,96

 

SEZIONE VERIFICATA

 

CALCESTRUZZO

- Dopo aver inserito i dati relativi alla grandezza del solaio ed aver trovato l'area di influenza del pilastro, calcolo il peso unitario della trave_p e della trave_s

trave= area della sezione (0,30 x 0,55) mq x peso specifico 24 KN/m3 = 3,96KN/m

 

Posso calcolare il carico dovuto al peso proprio delle travi 

q trave= (trave p x L1 x 1,3) + (trave s x L2 x 1,3) = 51,48 KN

 

- Per calcolare il valore complessivo del carico agente, inserisco i valori dei carichi agenti sul solaio: carichi strutturali, carichi permanenti e carichi accidentali. 

q solaio= (1,3 x qs + 1,5 x qp + 1,5 x qa) x A = 263,77 KN

 

- Per finire calcolo lo sforzo di compressione N

N= (q trave x q solaio) x n piani= 946 KN

 

 

Posso così calcolare l’ area minima necessaria affinché il materiale non entri in crisi.

- Inserisco i dati relativi al materiale:

 

la tensione di snervamento fck = 40 MPA

 

 ricavo :

 f_cd =  22,7 MPa

 

Amin = 417,2 cm² 

 

bmin = 20,4 cm

 

- Sapendo che Il modulo di elasticità E = 210000 MPa, β =1 e l’altezza del pilastro è di 3 m, posso calcolare:

valore massimo di snellezza λ_{max =} 95,62

valore minimo del raggio di inerzia ρ_min = 3,14 cm

la grandezza della base minima (b min) = 10,87 cm, che ingegnerizzo a b = 40 cm

l’altezza minima (h min) = 10,43 cm, che ingegnerizzo a  h = 40 cm

 

- Verifico che A_design > A_min

 

1600 cm² > 417,2 cm²                 

 

- Per il calcestruzzo devo inoltre verificare che la tensione massima sia minore della resistenza di progetto: σmax <  fcd

 

14,15 MPA <  22,7 MPA           

 

SEZIONE VERIFICATA

1. Dimensiono una travatura reticolare partendo dal modello di griglia semplice che mi fornisce il programma SAP, decidendo il numero di campate e i metri di ogni campata nelle 3 direzioni. 
Disegno la campata di base e la copio e incollo (cmd. COPY e PASTE) riempiendo tutta la griglia, curandomi di non sovrapporre le linee (per questo mi sarà utile il comando MERGE DUPLICATES)

2. Assegno alla struttura:
-i vincoli esterni (cerniere)

- i vincoli interni nei nodi (cerniere interne, potendo assumere che non ci sono incastri ma cerniere)
Definisco quindi la sezione delle aste (PIPE) e il carico esterno nei nodi superiori della struttura


3. Avvio quindi l'analisi della struttura. Trovo così la deformata e i diagrammi del solo sforzo normale sulle singole aste.
Poichè si tratta di una travatura reticolare, le aste sono sollecitate solamente a sforzo assiale (di compressione o trazione).

 

A questo punto posso procedere all'Analisi delle aste.
4. Per analizzare i valori di ogni asta esporto i valori dei singoli sforzi da SAP a una tabella excell. I valori positivi si riferiscono alle aste tese, e quelli negativi alle aste compresse. Mettendo in ordine i valori, posso trovare le aste più compresse rispettivamente a trazione e a compressione. 
Una volta riportati i valori di ogni asta nella tabella excell, posso definire la sezione ingegnerizzata di ogni profilato.

Per quanto riguarda le aste TESE, tramite N, fyk e gamma, ricavo l'area minima e posso quindi dimensionare i vari profilati con la tabella dei profilati metallici.

(qui le aste più sollecitate a trazione)

Per dimensionare le aste COMPRESSE, calcolo l'area minima come ho fatto in precedenza con le aste tese, ma successivamente prima di passare al dimensionamento delle sezioni devo considerare il fattore instabilità.
Inserisco quindi in tabella i valori relativi alla luce delle aste e all'elasticità del materiale. Calcolo l'inerzia minima per sforzo di compressione e infine ingegnerizzo la sezione e ne verifico la snellezza.

Per questa nuova esercitazione, in cui si deve dimensionare un pilastro soggetto a sforzo normale realizzato in legno, cls e d acciaio, ho utilizzato la pianta delle carpenterie della prima esercitazione ripetendola per quattro piani, ottenendo quindi una struttura a più livelli. Per il dimensionamento dei pilastri si è scelto di prendere in esame quello su cui grava un sforzo normale maggiore ovvero quello centrale alla struttura su cui non solo grava il peso portato dalla sua area d’influenza ma anche quello dei 3 pian soprastanti.

 

PILASTRO IN LEGNO

4.1

4.2

4.3

Nella prima parte dell’esercitazione ho ricavato lo sforzo normale agente sul  pilastro centrale.( 4.4) Come prima cosa ho calcolato l’area d’influenza agente sul pilastro e subito dopo mi sono ricavato il peso strutturale delle travi primari e secondarie moltiplicando l’area della sezione per il suo peso specifico. In particolare la trave principale di sezione (30 x 50 cm) con un peso specifico di 5 kN/mc ha un peso unitario di 0,75 kN/m.  Con questi dati ho potuto ricavare il carico dovuto al peso proprio delle travi sul pilastro (qt)  sommando il prodotto tra il peso unitario e la lunghezza delle travi confluenti sul pilastro e moltiplicandolo per il coefficiente di sicurezza 1.3. Utilizzando il carico strutturale (qu) del solaio, che avevo precedentemente  calcolato nella prima esercitazione,  e moltiplicandolo per il numero di piani della struttura  ho ottenuto lo sforzo normale(N) agente sul pilastro in esame.

4.4

Nella seconda parte dell’esercitazione ho come prima cosa predimensionato il pilastro. (4.5)

Per fare ciò mi è servito conoscere la resistenza a compressione del legno lamellare (fck), il coefficiente di sicurezza (γm), il coefficiente  riduttivo (kmod), il modulo di resistenza elastica (E), (β) il coeficente che rispecchia i gradi di vincolo del pilastro e l’altezza del pilastro (l).

In questo modo ho potuto ricavare la  resistenza di progetto (fcd) facendo il rapporto tra la resistenza compressione e il coefficiente di sicurezza. Cosi ho calcolato la snellezza massima (λmax) data dal  prodotto tra π e la radice del rapporto tra il modulo elastico e la resistenza di progetto. Con la snellezza massima ho potuto ricavare il raggio d’inerzia minimo (ρmin) ottenuto dal rapporto tra la lunghezza del pilastro e la sua snellezza. Dopo essermi calcolato l’area minima che deve avere il pilastro per resistere a compressione (Amin), facendo il rapporto tra lo sforzo normale e la resistenza di progetto, ho potuto ricavarmi la base minima del pilastro (b min) facendo il prodotto 2 e la radice quadrata del prodotto tra tre e il raggio minimo d’inerzia, e poi l’altezza minima (h min) facendo il rapporto tra l’area minima e la base minima.

4.5

Nell’ultima parte dell’esercizio ho dimensionato la sezione in modo tale che rispondesse ai valori trovati ed in particolare la base e l’altezza della sezione scelta fossero maggiori di quelle minime e di conseguenza l’area di questa fosse maggiore di quella minima per resistere a compressione. In questo casa la sezione da me scelta 20x30 cm risulta essere verificata.(4.6)

4.6

 

PILASTRO IN CLS

4.7

4.8

4.9

Come nel caso del pilastro in legno come prima cosa partendo dalla geometria e dai pesi della struttura ho ricavato lo sforzo normale agente sul pilastro più sollecitato. (4.10)

4.10

Conoscendo il modulo di elasticità (E) del cemento, la sua resistenza a rottura (fck) e ), (β) coefficiente dato dai vincoli agenti sul pilastro ho potuto ricavare: la resistenza di progetto (fcd), l’area minima del pilastro (Amin), la snellezza del pilastro(λmax),il raggio d’inerzia minimo (ρmin), la base minima(b min) e l’altezza minima (h min).( 4.11)

4.11

Con i dati ricavati ho potuto dimensonare il mio pilastro in modo tale che le sue dimensioni fossero maggiori rispetto alle minime ricavate per stare in sicurezza ed in particolare che l’area di desing (A design) fosse maggiore dell’area minima affinche fosse verificata per lo sforzo normale.(4.12)

4.13

Tuttavia il pilastro di cemento necessita di un’ulteriore verifica essendo sottoposto a presso flessione in quanto il nodo con la trave è composto da un incastro e quindi trasmette anche il momento oltre che lo sforzo normale. Per verificarlo a pressoflessione impongo che la tensione massima

(σmax) sia minore della resistenza di progetto.(4.14) La tensione massima la ricavo in funzione dello sforzo normale e del momento, trasmessi dalla trave al pilastro, facendo la somma del rapporto tra lo sforzo normale e l’area del pilastro e il rapporto tra il momento(Mt) e il modulo di resistenza a flessione (W). Il modulo di resistenza a flessione lo calcolo dividendo per sei il prodotto tra la base e l’altezza al quadrato della sezione del pilastro.

Per calcolare il momento invece devo prima calcolarmi alo slu il carico distribuito sulla trava (qt), ovvero facendo la somma del prodotto di uno 1,3 per il carico strutturale con  il prodotto di 1,5 e il carico permanente e con il prodotto di 1,5 ed il carico accidentale.

A questo punto posso calcolarmi il momento agente sul pilastro dividendo per 12 il prodotto tra il carico distribuito sulla trave e l’interasse principale al quadrato.

Ricavati questi dati posso finalmente verificare che la tensione massima è inferiore alla forza di progetto e che quindi la sezione da me scelta di 35x40 cm risulta essere verificata!

4.14

 

 

PILATRO IN ACCIAIO

4.15

4.16

4.17

 

Per la realizzazione del solaio in acciaio, calcolato nella prima esercitazione, mi sono servito di IPE 330 dal peso di 0,49 kN/m, per le travi principali ed IPE 140, dal peso di 0,129 kN/m, per le travi secondarie.

Considerando i diversi pesi degli elementi strutturali, come per le altre esercitazioni mi sono ricavato lo sforzo normale portato dal pilastro maggiormente sollecitato della struttura.(4.18)

4.18

Conoscendo le caratteristiche dell’acciaio ed i tipi di vincolo del pilastro ho potuto calcolare, come nei casi precedenti: l’area minima della sezione(A min), la snellezza (λmax)e il raggio minimo d’inerzia(ρmin).

Ma al contrario dei casi precedenti per scegliere la sezione, non mi sono dovuto ricavare la base e l’altezza minima del pilasto ma mi sono dovuto servire di un ulteriore dato ovvero il momento d’inerzia minimo (I min) che ho ricavato moltiplicato l’area minima per il quadrato del raggio d’inerzia.(4.19)

4.19

A questo punto dal profilario di elementi HEA ho potuto scegliere quello che non solo ha un area superiore a quella minima ma anche un momento di inerzia maggiore a quello minimo in modo tale che garantisca la sua stabilita a sforzo normale. Nel caso da me calcolato ho soddisfato la verifica con un profilo HEA 180. (4.20)

4.20

                              

Lo scopo di quest’esercitazione è quello di dimensionare un elemento soggetto a sforzo normale centrato di compressione, dove la deformazione Δl < 0 viene definita contrazione. In questo caso è necessario considerare, oltre alla rottura del materiale, anche il fenomeno di instabilità euleriana.  A tal fine sarà fondamentale definire due grandezze: l’area e il momento d’inerzia minimo della sezione.

L’area minima che deve essere ricavata, in modo da evitare lo schiacciamento del materiale, si ottiene eguagliando la tensione massima sulla sezione (σ_max) alla resistenza di progetto del materiale (f_cd).

σ_max = f_cd

σ_max = N / A_min

quindi:

N/A_min = f_cd

A_min = N / f_cd

Il momento di inerzia minimo della sezione si ottiene eguagliando la tensione massima sulla sezione (σ_max) alla tensione critica (σ_crit) generata del carico critico euleriano ovvero la forza di compressione che innesca il fenomeno di instabilità.

Per ricavare la tensione critica è dunque necessario definire il carico critico euleriano (N_crit).

N_crit= π² x E x I_min / (β x L)²

Dove:

E = modulo di elasticità del materiale

I_min= il minore momento di inerzia tra I_x e I_y

β = coeff. adimensionale relativo al tipo di vincolo (nella figura sottostante)

L = lunghezza dell’elemento

Attraverso le seguenti relazioni si giunge alla definizione di carico critico euleriano:

I_min = A x ρ_min²

λ = L₀ x ρ_min

dove L₀ è la luce libera di inflessione ed è pari a βL

N_crit = π² x E x A / λ²

σ_crit = N_crit / A = π² x E / λ²

Essendo l’instabilità un fenomeno impossibile da controllare e dovendo mettere in relazione la σ_crit con la σ_max (ricordando che σ_max = f_cd), si impone f_cd < σ_max in modo tale che la tensione raggiunga per prima la resistenza schiacciamento del materiale, con conseguente rottura.

 

Dimensionamento pilastro in calcestruzzo

Prima di tutto viene individuata l’area di influenza del pilastro.

Area = L₁ x L₂

Il secondo passo è quello di individuare lo sforzo normale di compressione. A tal fine è indispensabile calcolare il carico dovuto al peso delle travi sul pilastro, il carico del solaio ed il numero dei piani dell’edificio.

 

Carico del peso delle travi sul pilastro

Peso proprio delle travi [KN/m] = Area [m²] x Peso specifico [KN/m³]

Area_p = (0,3*0,4) [m²] *25 [KN/m] = 3 [KN/m]

Area_s = (0,3*0,4) [m²] *25 [KN/m] = 3 [KN/m]

Quindi,

q_trave = 3*1,3*5 + 3*1,3*3,5 = 33,15 [KN]

Carico del solaio

I carichi strutturali, permanenti ed accidentali del solaio sono stati recuperati dalla prima esercitazione per individuare il carico totale del solaio sul pilastro, che si ricava dall’equazione di combinazione dei carichi (in questo caso sarà la combinazione dei carichi allo SLU).

Considerato che il numero dei piani dell’edificio è pari a 5, abbiamo ora tutti i valori necessari al calcolo di N:

N [KN] = (q_trave + q_trave) x n_piani

Si è scelta come classe di calcestruzzo C40/50 e, successivamente, è stata determinata la resistenza di progetto a compressione.

f_cd = f_ck / γ_m

Quindi è stata calcolata l’area minima e la base minima.

A_min = N / f_cd

b_min = √A_min

Inserendo il modulo di elasticità del calcestruzzo, il coefficiente di vincolo β e l’altezza dell’asta, si ottengono la snellezza, il raggio di inerzia minimo e la base minima.

λ_max = π x √(E / f_cd)

ρ_min = L₀ / λ_max

La base minima è calcolata come segue:

b_min = 2 x √(3 x ρ_min)

A questo punto la base minima deve essere opportunamente ingegnerizzata. Con l’area minima e la base minima si ottiene l’altezza minima, la quale va anch’essa ingegnerizzata opportunamente per calcolare infine l’area di design ed il momento di inerzia di design.

A_design = b x h

I_design = (b³ x h) / 12

Nel calcestruzzo è necessaria la verifica del pilastro a presso-flessione poiché, essendo il nodo trave-pilastro un incastro, trasmette momento. Per tale verifica si impone

σ_max ≤ f_cd

dove, σ_max è pari alla somma dello sforzo normale di compressione ed il momento trasmesso:

Lo sforzo normale di compressione è noto mentre il momento trasmesso viene calcolato come:

M_t = q_t x L_p² / 12

dove q_t rappresenta il carico distribuito sulla trave principale:

q_t = (1,3 x q_s + 1,5 x q_p + 1,5 x q_a ) x L_s

Il modulo di resistenza alla compressione è calcolato come segue:

W_max = b x h² / 6

Quindi per la verifica della sezione a presso-flessione si impone:

In questo caso risulta verificata.

 

Dimensionamento pilastro in legno

Viene individuata l’area di influenza del pilastro.

Area = L₁ x L₂

Carico del peso delle travi sul pilastro

Si calcola il peso delle travi principali e secondarie moltiplicandole per il loro peso specifico ed ottenendo il contributo totale del peso delle travi.

Peso proprio delle travi [KN/m] = Area [m²] x Peso specifico [KN/m³]

trave_p = (0,3*0,35) [m²] *25 [KN/m] = 2,63 [KN/m]

trave_s = (0,3*0,25) [m²] *25 [KN/m] = 1,88 [KN/m]

Quindi,

q_trave = 2,63*1,3*5 + 1,88*1,3*3,5 = 25,65 [KN]

 

Carico del solaio

I carichi strutturali, permanenti ed accidentali del solaio sono stati recuperati dalla prima esercitazione per individuare il carico totale del solaio sul pilastro, che si ricava dall’equazione di combinazione dei carichi (in questo caso sarà la combinazione dei carichi allo SLU).

Poiché il numero dei piani dell’edificio è pari a 5, abbiamo ora tutti i valori necessari al calcolo di N:

N [KN] = (q_trave + q_trave) x n_piani

La resistenza a compressione si ottiene dopo aver scelto la classe di legno C24 con una f_ck = 24 MPa

f_cd = f_ck x k_mod / γ_m

dove k_mod è un coefficiente correttivo pari a 0,8 e γ_m è un coefficiente di sicurezza pari a 1,45. Quindi è stata calcolata l’area minima.

A_min = N / f_cd

Ora è necessario individuare il raggio di inerzia minimo che ci permetterà di ricavare la base minima che deve avere la sezione. Inserendo nel file Excel il modulo di elasticità E, il valore β e l’altezza del pilastro l, si ricava la snellezza massima ed il raggio di inerzia minimo.

λ_max = π x √(E / f_cd)

ρ_min = L₀ / λ_max

La base minima è calcolata come segue:

b_min = 2 x √(3 x ρ_min)

A questo punto la base minima deve essere opportunamente ingegnerizzata. Con l’area minima e la base minima si ottiene l’altezza minima, la quale va anch’essa ingegnerizzata opportunamente per calcolare infine l’area di design ed il momento di inerzia di design.

h = A_min / b

A_design = b x h

I_design = (b³ x h) / 12

 

 

Dimensionamento pilastro in acciaio

Viene individuata l’area di influenza del pilastro.

Area = L₁ x L₂

Carico del peso delle travi sul pilastro

Si calcola il peso delle travi principali e secondarie moltiplicandole per il loro peso specifico ed ottenendo il contributo totale del peso delle travi.

Peso proprio delle travi [KN/m] = Area [m²] x Peso specifico [KN/m³]

Per la trave principale si sceglie un IPE 270 CON PESO DI 36.1 Kg/m e, per la trave secondaria, un IPE 200 con peso di 22.4 kg/m.

trave_p = 0,36 [KN/m]*78,5 [KN/m] = 28,33 [KN/m]

trave_s =  0,22 [KN/m]*78,5 [KN/m] = 17,58 [KN/m]

Quindi,

q_trave = 28,33*1,3*5 + 17,58*1,3*3,5 = 264,04 [KN]

Carico del solaio

I carichi strutturali, permanenti ed accidentali del solaio sono stati recuperati dalla prima esercitazione per individuare il carico totale del solaio sul pilastro, che si ricava dall’equazione di combinazione dei carichi (in questo caso sarà la combinazione dei carichi allo SLU).

Poiché il numero dei piani dell’edificio è pari a 5, abbiamo ora tutti i valori necessari al calcolo di N:

N [KN] = (q_trave + q_trave) x n_piani

La resistenza a compressione si ottiene dopo aver scelto la classe di acciaio S275 con una f_yk = 275 MPa

f_yd = f_yk / γ_m

dove γ_m è un coefficiente di sicurezza pari a 1,05. Quindi è stata calcolata l’area minima.

A_min = N / f_yd

Ora è necessario individuare il raggio di inerzia minimo che ci permetterà di ricavare la base minima che deve avere la sezione. Inserendo nel file Excel il modulo di elasticità E, il valore β e l’altezza del pilastro l, si ricava la snellezza massima ed il raggio di inerzia minimo.

λ_max = π x √(E / f_yd)

ρ_min = L₀ / λ_max

A questo punto è necessario calcolare il momento di inerzia minimo:

I_min = A x ρ²_min

Conoscendo I_min si può scegliere la sezione del pilastro sul formulario, verificando che:

• L’area di design sia maggiore/uguale rispetto a quella trovata
• Il momento di inerzia sia maggiore/uguale rispetto a quello trovato
• Il raggio di inerzia sia maggiore/uguale rispetto a quello trovato

Quindi viene individuata la sezione del pilastro HEA260, con le seguenti misure:

A_design = 86,80 > 84,9 [cm²]

I_design = 3668 > 782 [cm⁴]

ρ_design = 6,50 > 3,04 [cm]

 

Questa esercitazione prevede il dimensionamento di una mensola nelle tre diverse tecnologie: Legno, Acciaio e Calcestruzzo armato.

Osservando la pianta, risulta evidente che la trave a sbalzo più sollecitata è quella centrale, perchè quella con area d'influenza maggiore.

Si procede, dunque, con il dimensionamento della mensola, basandosi sugli stessi carichi e le stesse stratigrafie di solaio dell' EXE1_Dimensionamento di un solaio per un solaio in legno, acciaio e calcestruzzo armato.

 

SOLAIO IN LEGNO

Carico strutturale (Qs) = 0,265 KN/mq

Carico permanente (Qp) = 2,66 KN/mq

Carico accidentale (Qa) = 2,00 KN/mq

Dopo aver inserito i valori dei carichi sul foglio Excel, e avendo così ottenuto il carico totale Q, inserendo anche la luce l = 2 m, si ricava  il valore del Momento massimo che, trattandosi di una mensola, è definito dall'equazione:

M_max = ql²/2.

A questo punto, dopo ver scelto la tipologia di legno, legno lamellare GL 24h, bisogna inserire il valore di resistenza a flessione caratteristica fm,k = 24 MPa.

Si ottiene così la tensione ammissibile sig_d (N/mm²) = 0,8 x kmod / 1,45, dove:

- 0,8 è il coefficiente della durata del carico (kmod);

- 1,45 è il coefficiente parziale di sicurezza del materiale (γm).

Impostando un'ipotetica base b = 20 cm, si ottiene l'altezza minima h_min, ossia il valore minimo che deve avere l’altezza della sezione

Questa altezza minima deve però essere ingegnerizzata, deve cioè essere scelto un valore di altezza superiore ad hmin. 

Si inserisce quindi anche il valore del modulo elastico E = 8.000 N/mm².

In questo modo il foglio Excel determina:

- il momento d’inerzia I_x = b x h³/12;

- l’abbassamento massimo v_max = q x l⁴/ 8 x E x I_x

- il suo rapporto con la luce l/v_max.

Se quest'ultimo valore soddisfa la condizione l/v_max ≥ 250 la sezione può definirsi verificata. 

LA SEZIONE E' VERIFICATA!

 

SOLAIO IN ACCIAIO

 

Carico strutturale (Qs) = 2,028 KN/mq

Carico permanente (Qp) = 2,95 KN/mq

Carico accidentale (Qa) = 2,00 KN/mq

 

Dopo aver inserito i valori dei carichi sul foglio Excel, e avendo così ottenuto il carico totale Q, inserendo anche la luce l = 2 m, si ricava  il valore del Momento massimo che, trattandosi di una mensola, è definito dall'equazione:

M_max = ql²/2.

 A questo punto si inserisce la tensione di snervamento del Fe 430/ S275, fy,k = 275 MPa, e si ottiene così:

- la tensione di progetto f_d = 293,13 N/mm²

- il modulo di resistenza W_x = 226,18 cm³.

Dopo aver ottenuto il modulo di resistenza, bisogna ingegnerizzare la sezione. Quindi si inserisce il valore del momento d’inerzia I_x del profilo, che ha come modulo di resistenza W_x, un valore maggiore di quello trovato

Dopo aver scelto il profilo, che in questo caso è una trave IPE 220, non resta altro che inserire il valore del modulo elastico E = 210.000 N/mm².

In questo modo il foglio di calcolo determina:

- l’abbassamento massimo v_max = q x l⁴/ 8 x E x I_x

- il suo rapporto con la luce l/v_max.

Se quest'ultimo valore soddisfa la condizione l/v_max ≥ 250 la sezione può definirsi verificata.

LA SEZIONE E' VERIFICATA!

 

SOLAIO IN CALCESTRUZZO ARMATO

Carico strutturale (Qs) = 2,536 KN/mq

Carico permanente (Qp) = 2,345 KN/mq

Carico accidentale (Qa) = 3,00 KN/mq

Dopo aver inserito i valori dei carichi sul foglio Excel, e avendo così ottenuto il carico totale Q, inserendo anche la luce l = 2 m, si ricava  il valore del Momento massimo che, trattandosi di una mensola, è definito dall'equazione:

M_max = ql²/2.

A questo punto si sceglie la tipologia di acciaio per l'armatura del cls, B450C, e si inserisce la tensione di snervamento fy = 450 MPa; in questo modo si ottiene la tensione di progetto fd_f.

Si inserisce inoltre anche fck = 60 MPa, e si considera una base b = 20 cm

Si ottiene in questo modo un'altezza minima  H = 25,30 cm. Questa altezza va ingegnerizzata, deve cioè essere scelto un valore di altezza superiore ad H. Quindi l'altezza della sezione della trave sarà uguale a Hd = 35 cm.

L'ultimo passaggio è l'inserimento del modulo elastico dell'acciaio dell'armatura E = 21000 N/mm².

In questo modo il foglio di calcolo determina:

- il momento d’inerzia I_x = b x h³/12;

- l’abbassamento massimo v_max = q x l⁴/ 8 x E x I_x

- il suo rapporto con la luce l/v_max.

Se quest'ultimo valore soddisfa la condizione l/v_max ≥ 250 la sezione può definirsi verificata. 

LA SEZIONE E' VERIFICATA!