SdC(b) (LM PA)

Questa prima esercitazione prevede l’analisi ed il dimensionamento di massima di una struttura reticolare spaziale, attraverso il supporto del programma SAP 2000.

Le travature reticolari sono strutture costituite da un insieme di aste collegate fra loro mediante delle cerniere interne (nodi), nelle quali sono applicati i carichi che sollecitano la struttura; di conseguenza ogni asta è sollecitata secondo la congiungente dei nodi ed è quindi soggetta soltanto a sforzo normale, di trazione (TIRANTE)  o di compressione (PUNTONE). 

1_ Per creare una struttura selezionare FILE – NEW MODEL, impostare l’ UNITA’ DI MISURA corretta (KN, m, C) e procedere con il metodo di disegno più opportuno, in questo caso GRID ONLY.

2_Nella finestra successiva inserire il numero di linee della griglia necessarie per disegnare le aste della struttura (in base alle direzioni dei piani) e regolarne l’interasse.

3_ In tal modo otterremo la griglia voluta. Per disegnare la struttura selezionare nella barra laterale il comando DRAW FRAME/CABLE e tracciare le aste seguendo le linee della griglia. 

4_ Disegnare la struttura facendo attenzione a non sovrapporre le aste.

5_ Dopo aver ottenuto la struttura bisogna assegnare i vincoli esterni. Selezionare i punti in cui questi ultimi si vogliono posizionare e successivamente cliccare su ASSIGN – JOINT – RESTRAINTS e scegliere i vincoli da inserire, in questo caso cerniere. 

6_ Essendo una struttura reticolare è necessario che le aste siano collegate tra loro attraverso delle cerniere interne, così da poter reagire soltanto a sforzo normale. Per fare ciò occorre selezionare tutta la struttura e cliccare su ASSIGN – FRAME – RELEASES/PARTIAL FIXITY e spuntare il rilascio del momento sia all’ inizio che alla fine di tutte le aste.

7_ Per definire il materiale selezionare DEFINE – MATERIALS e scegliere quello desiderato. Per questa prima analisi è stato impostato un acciaio di base. 

8_ Per definire la sezione delle aste procedere cliccando su DEFINE – SECTION PROPERTIES – FRAME SECTIONS – ADD NEW PROPERTY. Una volta opzionata quella desiderata, in questo caso un tubolare cavo, si aprirà una nuova finestra in cui sarà possibile modificare il nome e le caratteristiche della sezione. Per questa prima analisi sono stati lasciati i valori di default.

9_ Per assegnare la sezione alle aste bisogna selezionarle, premere su ASSIGN – FRAME – FRAME SECTIONS ed indicare quella voluta. In tal modo comparirà il nome della sezione su ogni asta. 

10_ E’ ora necessario inserire il carico; essendo una reticolare, vanno assegnate delle forze concentrate sui nodi superiori della struttura. Per selezionarli con più facilità è possibile impostare la vista 2D da VIEW – SET 2D VIEW – ASSI X,Y ed impostare la quota in altezza sulla quale si trovano i nodi superiori, in questo caso Z=2.

11_ Da questa visuale, dopo aver selezionato i nodi superiori centrali della struttura premere ASSIGN – JOIN LOADS – FORCES. Prima di procedere, è necessario creare un nuovo caso di carico in cui il moltiplicatore di peso proprio della struttura sia pari a zero. Dopo aver inserito tale valore e dopo aver assegnato il nome, aggiungere il nuovo caso e selezionarlo nel momento in cui si assegna il valore alle forze concentrate, direzionandole verso il basso.

12_ Ripetere i stessi passaggi per i nodi superiori perimetrali, assegnando però un valore di forze pari alla metà di quello usato precedentemente. Questo avviene perché i nodi esterni interessano   la metà dell’area d’ influenza rispetto a quelli interni. Otterremo così il modello della struttura, definita così in ogni aspetto.

13_ A questo punto si può far partire l’analisi, selezionando esclusivamente il caso di carico in cui il peso proprio della struttura non è considerato. Per una verifica finale si possono controllare i valori del momento e del taglio; se il modello reticolare è stato lavorato nel modo giusto, essi dovranno essere pari a zero. Otterremo infine la deformata ed i valori dello sforzo assiale con i quali sarà possibile progettare un dimensionamento di massima.

Grazie a SAP2000 è possibile importare su EXCEL i valori dello sforzo assiale di ogni asta, sia di compressione che di trazione, per poi poter procedere al dimensionamento. 

ALLEGATO: Tabella Excel sforzi assiali 

Per una struttura reticolare la sezione più indicata per le aste è un tubolare cavo, inoltre si sceglie un tipo di acciaio duttile, l’ S235.

-DIMENSIONAMENTO ASTE SOGGETTE A TRAZIONE

1_ Rottura  -->   Area minima = N/fd

Ricavato il valore dell’area minima, derivante dalla formula di Navier che in questa fase di dimensionamento tiene conto della tensione di snervamento fd, si possono indicare profilati che abbiano un’ A>Amin.

Sono stati scelti 4 profili per le aste tese:

33,7 x 2,6 mm

42,4 x 2,6 mm

42,4 x 3,2 mm

60,3 x 2,9 mm

ALLEGATO: Tabella Excel aste tese

-DIMENSIONAMENTO ASTE SOGGETTE A COMPRESSIONE

1_ Rottura  -->   Area minima = N/fd

2_ Instabilità euleriana  -->  Momento d’inerzia minimo = Amin/ρmin^2

Oltre all’ area minima, necessaria affinché la sezione resista a rottura, bisogna valutare il risultato della seconda formula. Quest’ ultima deriva dal carico critico eureliano, superato il quale l’asta subisce uno sbandamento; per evitare che questo accada è bene tener conto di parametri come il momento d’inerzia ed il raggio d’inerzia, valori dipendenti dal materiale, dalla lunghezza delle aste e dai loro rispettivi vincoli.

Ricavati i valori minimi delle caratteristiche richieste si può effettuare il dimensionamento di massima, indicando profilati che abbiano  A>Amin e I>Imin, facendo però attenzione anche al parametro della snellezza che per normativa non dovrà mai essere maggiore di 200.

Sono stati selezionati 8 profili per le aste compresse, di cui 4 in comune con le aste tese:

33,7 x 2,6 mm

42,4 x 2,6 mm

42,4 x 3,2 mm

48,3 x 3,6, mm

48,3 x 3,2 mm

60,3 x 2,9 mm

76,1 x 2,6 mm

76,1 x 3,6 mm

ALLEGATO: Tabella Excel aste compresse

Dimensionamento travatura reticolare:

 

Una volta assegnate le cerniere esterne ed interne posso andare a inserire i miei carichi sui vari nodi.

2- Calcolo peso solaio

Il valore delle forze che saranno poi disposte sui nodi le ho trovate andando ad analizzare il peso del solaio in acciaio. Quindi trovandomi il qs (carico strutturale)

qp (carico permanente) qa (carico accidentale) posso trovarmi il qu cioè il carico ultimo. I vari carichi li trovo andando a sommare il peso di ogni materiale

considerando 1mq di solaio.

I risultati trovati saranno poi moltiplicati per un coefficiente di sicurezza che varia in base al tipo di carico.  e moltiplicati per l'interasse. Alla fine dovrò trovarmi una forza chenpoi sarà quella che prenderò in considerazione.

 

qu =  40 KN 

 

Tornando su SAP2000 posso inserire le forze puntuali che varieranno in base all’area d’influenza del nodo.

Prima d’inserire le forze mi assicuro di lavorare sul livello giusto facendo lo stesso procedimento di prima :

View , Set 2D , cambio il livello su quello superiore, cioè dove le forze cadranno.

 Assegno le forze in base all’area d’influenza:

- a quelle centrali darò F = 40 KN

- a quelle che cadono sul perimentro esterno darò F/2 = 20 KN

- agli spigoli metterò F/4 della forza = 10 KN

 

Per assegnare le forze, prima evidenzio i nodi interessati poi utilizzero i comandi : Assign , Joint loads , Forses , mi creo un nuovo carico che chiamerò FORZE ,

su “self Weight multiplier” metto zero per non considerare il peso proprio e poi selezione Add new load pattern .

Esempio della forza applicata sul lato perimetrale della reticolare che avrà un valore di F = 20 KN

Adesso ho inserito tutte le forze sui vari nodi. Ora posso fare la mia analisi. Analyse , Run

Il programma permette di poter visionare la deformata e i vari diagrammi del Momento ,Taglio e Normale.

I valori gialli sono quelli di trazione mentre i valori rossi sono di compressione.

Gli unici valori che troveremo nei diagrammi saranno quelli dello sforzo assiale. 

Per visualizzare le tabelle con tutti i valori della struttura vado su : Display , Show tables , spunto la casella Analyses results e andando su

Select load pattern seleziono la forza che ho creato. La tabella che noi dovremmo andare a considerare sarà Elements-forces-frames  perché

ci fornisce i valori e le caratteristiche delle aste sollecitate e dello sforzo normale. 

Ora dobbiamo importare le tabelle in Exel attraverso i comandi: File, export current table , to exel

Una volta aperta la tabella su Exel:

- ordino i vari valori della casella station dal più piccolo al più grande ed elimino i valori diversi dallo zero.

- Ordino anche dal più piccolo al più grande i valori di P (normale) in modo da avere ben divisi i valori delle aste compresse (negativi) da quelle tese (positivi)

                                

                                           

Una volta ordinati i vari valori vado a dimensionare le aste utilizzando 2 diverse tabelle, una per il dimensionamento delle aste tese ed una per quello delle aste

compresse. Non dimensionerò tutte le aste ma prenderò i valori dello sforzo normale ogni 30/40 KN di differenza per un dimensionamento di massima.

 

 

TRAZIONE:

Sul dato N inserisco i valori di trazione delle aste che ho desiso di dimensionare, ad ogni valore si associa quindi un numero di asta ( in rosso sono evidenziate le aste diagonali)

Scelgo un acciaio S235  con i relativi valori di fyk ( coeff. di snervamento ) di 235 Mpa e  Ym (coefficiente di sicurezza)  pari a 1,05.

Per le aste tese basta calcolarsi l'Amin della sezione tramite la formula di  Navier σ=N/A dove σ non deve superare fyk

Con questi valori posso trovarmi fyd (tensione di progetto) e Amin (area minima di progetto).

Tramite le tabelle dei profilati metallici tubolari ,scaricati dal sito OPPO, posso attraverso il valore dell' Amin (dopo averlo ingegnerizzato Adesign)  posso trovarmi il valore della

sezione tubolare.

In questo caso per tutte le aste tese le sezioni trovate sono di 4 :

 

COMPRESSIONE: 

Sul dato N inserisco i valori di compressione delle aste che ho deciso di dimensionare ( faccio il modulo per inserire i valori positivi), il numero dell’asta ( evidenziate in rosso

le diagonali di lunghezza differente = 2,82 m ) 

Anche qui i valori di fyk e Ym sono i medesimi della trazione. 

Per quanto riguarda la conpressione, diversamente dalla trazione, devo tener conto anche di altri fattori  come il carico critico eureliano quindi vado a considerare nella mia analisi la

 l= lunghezza dell'asta , modulo di elasticità E= 210.000 Mpa e resistenza , per poter calcolare poi l'inerzia minima ed il raggio d'inerzia minima.

 

Attraverso l'inerzia min posso dimensionare il mio profilato andando a sceglierne uno con un inerzia maggiore facendo anche attenzione a che il valore dell'area del profilo scelto non sia inferiore all'area min.  

La snellezza deve  avere un valore  non superiore a 200. Anche  per quanto riguarda la compressione ,mi sono servita delle tabelle di OPPO per trovare la sezione del profilato
 

In questo caso per tutte le aste comprese le sezioni trovate sono di 4: 

 

 

 

In questa esercitazione stiamo analizzando i carichi e il dimensionamento delle aste di una struttura reticolare avente :

asta verticale di 3m ;

asta orizzontale di 2 m ;

asta obliqua di 3,6 m.

Costruisco in Sap un griglia di base di modulo di  2 x 2 x 3 . La copio nelle direzioni x e y fino ad ottenere una griglia di 3 x 4 moduli = 24 .

Inserisco le ceniere interne ed esterne .

Ipotizzo un pacchetto di solaio :

qs carichi strutturali :

lamiera gregata            0,4   KN/m²

massetto alleggerito     1,62  KN/m²

Tot.                             2,02  KN/m²

qp carichi permanenti :

pavimento                   0,4   KN/m²       

malta allettamento      0,72  KN/m²

isolante                      0,36  KN/m²   

impianti e tramezzi      1,5    KN/m².

Tot                             2,98  KN/m²

qa carichi accidentali :

residenziale                2        KN/m²

qu carico totale solaio :

qu = qs (1,3) + qp (1,5) + qa (1,5)    x     (Area Influenza)

= 10,096 KN/m²   x   4 m²   =   40,384   KN      (Area influenza A)  -  nodi al centro

= 10,096 KN/m²   x   2 m²   =   20,192   KN      (Area influenza B)  -  nodi al lato       

= 10,096 KN/m²   x   2 m²   =   10,096   KN      (Area influenza C)  -  nodi al bordo        

Progetto allo S.L.U. in nodi più sollecitati. 

Analizzo gli sforzi normali, poiché non sono presenti sforzi di taglio e momento. 

Importo i dati in excell.

In un altro foglio excell procedo quindi a dimensionale le aste :

inserisco il valore della normale;

calcolo l’Area minima : Amin  =  N / fyd

I beta in questo caso sono uguali a 1 perché ho due incastri agli estremi delle aste.

Calcoliamo l’inerzia minima  :  Imin  =  Amin  x (rho_min)²

Scelgo un profilato con Inerzia maggiore e verifico che la snelleza non sia maggiore di 200. 

Per prima cosa ho impostato l'unità di misura kN,m,C e dimensionato un elemento, a partire dalla griglia, che avesse i lati lungo x,y,z=4m

Ho costituito la travatura reticolare copiando prima gli elementi lungo x e poi lungo y fino ad ottenere un travatura 24X36m.

Ho definito la sezione degli elementi strutturali --> DESIGN->SECTION PROPERTIES-->FRAME SECTION-->PIPE materiale acciaio. ho scelto quindi dei tubolari in acciaio lasciando le misure di default di Sap2000 e il nome di default FSEC2.

Assegno quindi le sezioni. Seleziono la travatura ->ASSIGN-> FRAME SECTION-> seleziono FSEC2.

A questo punto mi occupo dei vincoli. Tutti quelli interni devono essere delle cerniere per far sì che la struttura sia isostatica. Effettuo quindi il rilascio dei momenti sia all'inizio che alla fine delle aste. Seleziono tutto->assign->FRAME->RELEASE.

Assegno ora i vincoli esterni che devono essere anch'essi delle cerniere. L'importante è che siano in corrispondenza dei nodi. Mi metto in pianta a quota 0. Scelgo i nodi dove inserire le cerniere->ASSIGN->JOINT->RESTRAINTS->CERNIERA.

Assegno il carico. Il modello è teorico e il carico quindi viene assegnato sui nodi (puntuale). Mi metto sul piano xy a quota 4m e seleziono la parte centrale della travatura-> ASSIGN->JOIN LOADS->FORCES. Da qui definisco il caso di carico perchè non devo considerare il peso proprio della struttura. Definisco quindi una forza F di intensità -200kN. - perchè rivolta verso il basso lungo Z.

Stessa cosa per i nodi perimetrali, non assegno un altro caso di carico ma modifico solamente l'intensità della forza. Questa volta questa sarà la metà di quelle centrali perchè l'area d'influenza è la metà. Assegno quindi una forza pari a -100kN.

La struttura è definita. Posso effettuare l'analisi dove faccio girare solo il caso F.

L'analisi mi deve mostrare che sia presente solamente lo sforzo assiale (maggiore in corrispondenza degli appoggi), il momento deve essere nullo e di conseguenza anche il taglio.

A questo visualizzo le tabelle che esporterò successivamente su Excel. CTRL+T-> select load pattern->F-> analisys results->ok. Seleziono  ELEMENT FORCES-FRAME, tabella da esportare su excel.

Elimino tutti gli elementi che non mi servono tra cui il taglio e il momento. Ordino la tabella.

A questo punto scarico la tabella dal PORTALE DI MECCANICA necessaria al dimensionamento sia delle aste compresse sia di quelle tese. Porto i valori trovati su Sap dalla tabella Excel dell'analisi sulla tabella del dimensionamento. Metto in valore assoluto tutti gli sforzi normali, scelgo l'acciaio S275. Essendo aste incernierate agli estremi il valore di Beta=1. Il coefficiente di sicurezza Gamma=1,05. Il modulo elastico dell'acciaio 21000000Mpa e la lunghezza dei tubolari dalla tabella elaborata da Sap. Grazie alle funzioni preimpostate della tabella excel posso ricavare la tensione caratteristica di progetto, l'area minima, la snellezza massima, il momento d'inerzia minimo e il raggio d'inerzia minimo necessario per il calcolo di aste compresse. Per le aste soggette a trazione necessino solamente dell'area minima. Utilizzando il profilario scaricato da oppo.it posso effettuare un dimensionamento di massima della travatura.

A questo punto dovrei assegnare ad ogni frame su Sap il tubolare da me scelto, prendendo questa volta in considerazione il peso proprio. Far partire nuovamente l'analisi e analizzare gli sforzi.

Ho deciso di riproporre la parte terminale – verso terra – di quella che ritengo essere un’interessante struttura reticolare spaziale disegnata da Burckhardt + Partner, l’MFO Park a Zurigo.

Parto scegliendo le unità di misura con le quali voglio lavorare (kilo newton, metri, gradi centigradi) ed impostando una griglia che mi servirà come base per la struttura.

Disegno quindi il “modulo base” che ripeto poi sia lungo l’asse x che lungo l’asse y (stravolgendo in parte il progetto di Burckhardt nel raddoppiare la campata; questo ai fini dell’esercitazione, così da applicare carichi diversi che tengano conto della diversa area d’influenza).

Definisco la sezione che voglio utilizzare (rinominata Tubolare_Esercitazione1) e la assegno alle aste della mia struttura. Rilascio i momenti su tutti nodi (quindi all’inizio ed alla fine di ogni asta), rendendoli cerniere interne.

Passo ad assegnare i vincoli esterni (8 cerniere) ed applico i carichi sui nodi: la forza concentrata F per quelli interni, la forza concentrata F/2 sopra i nodi del perimetro esterno (questo perché, come già accennato prima, i carichi agiscono su una superficie attorno al nodo che corrisponde alla metà della superficie sulla quale agiscono i carichi posti sui nodi interni).

Ora, l’analisi. Il programma permette di visionare la deformata, i diagrammi dello sforzo normale (il colore rosso sta a rappresentare un valore di compressione, quello blu di trazione) e quelli del momento. Questi ultimi – come da programma – risultano nulli. Alcune aste (quelle diagonali lungo il piano x-y ad altezza 2m) non presentano sforzo assiale (nel caso di carico concentrato); sono comunque necessarie come controventi, per far sì che la struttura sia reticolare e non labile.

Passiamo quindi al dimensionamento. Esportiamo da SAP su Excel una tabella che mostri ogni valore dello sforzo normale lungo le aste. La tabella può essere fortemente ridotta: il programma riporta infatti i valori dello sforzo normale su una singola asta quantomeno tre volte; essendo nel nostro caso lo sforzo costante lungo la stessa asta, possiamo mantenere un solo valore. Nel caso specifico, mantengo quello calcolato all’estremità dell’asta, così da sapere anche la lunghezza totale dell’asta alla quale è associato lo sforzo Normale (essendoci diverse aste diagonali, controllo su SAP la lunghezza delle aste). Divido quindi la tabella in due sottogruppi: aste compresse (in rosso) ed aste tese (in nero).

Finalmente il dimensionamento vero e proprio. I procedimenti saranno diversi a seconda che si parli di aste tese o di aste compresse. Nel primo caso, basterà confrontarsi con la resistenza del materiale; abbiamo quindi un solo fenomeno di crisi di cui tener conto: che la tensione nel materiale non raggiunga la tensione di progetto.

Nel caso delle aste compresse i fenomeni di crisi sono invece due. Uno avente sempre a che fare con la resistenza del materiale (come già detto per l’asta tesa), l’altro con l’instabilità euleriana (fenomeno particolarmente insidioso dal momento che le equazioni in gioco sono fortemente non lineari). Le incognite sono in questo caso due: l’area minima (necessaria per la rottura) ed il momento d’inerzia (necessario per l’instabilità).

Ma vediamo il ragionamento applicato al caso specifico, cominciando dalle aste tese.

Inserisco il valore dello Sforzo Normale di Trazione nella tabella Excel, scelgo un acciaio (S235) con i relativi valori di f_yk (coefficiente di snervamento, in questo caso 275 MPa) e γ_m (coefficiente di sicurezza pari a 1,05). Noti questi valori, posso trovarmi la tensione di progetto f_yd (uguale al rapporto tra il coefficiente di snervamento f_yk ed il coefficiente di sicurezza γ_m) e l’area minima di progetto A_min (uguale al rapporto tra il valore dello sforzo Normale e la tensione di progetto f_yd).

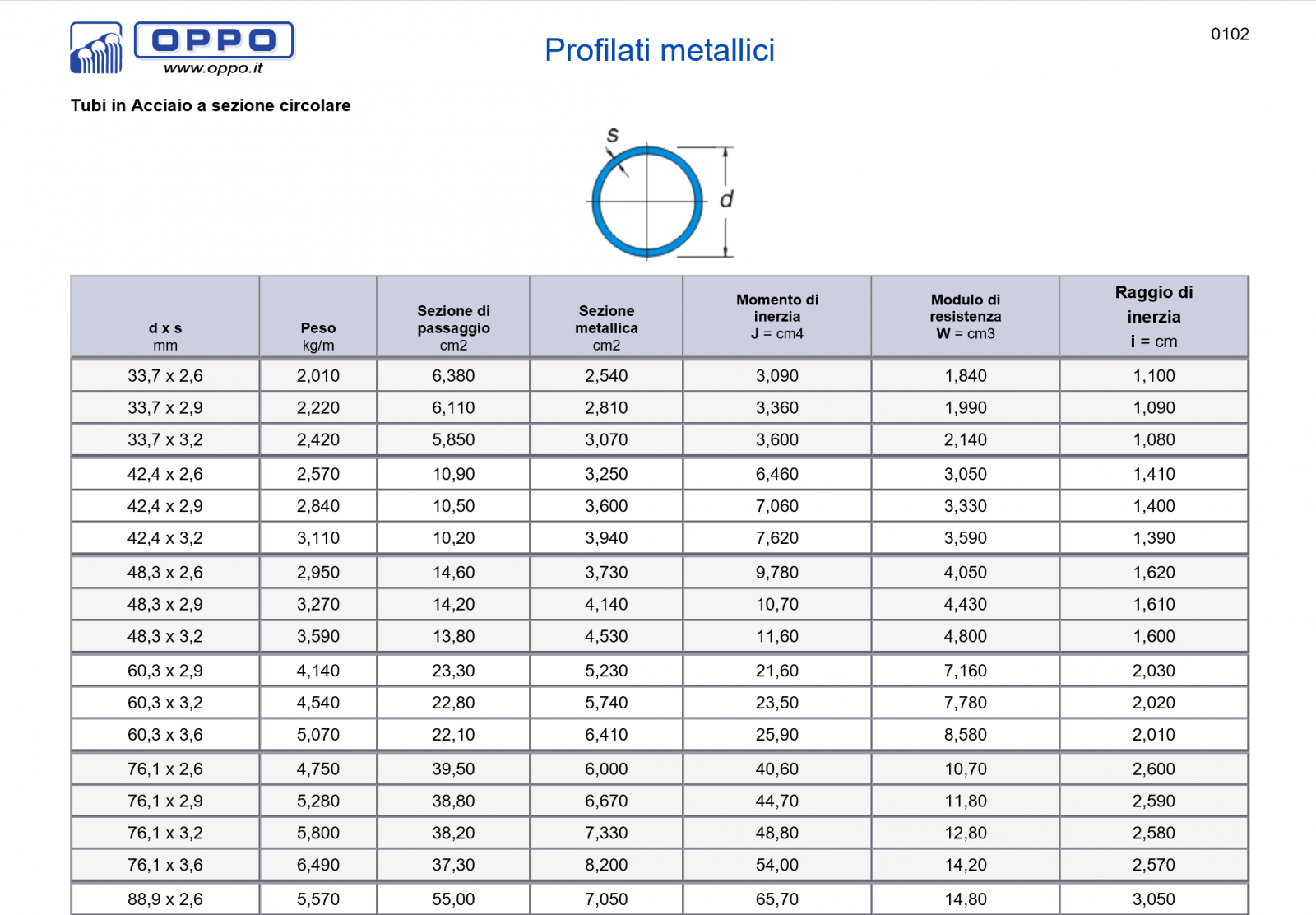
Con le tabelle dei profilati metallici tubolari sotto mano ed il valore ora noto di A_min (che va ingegnerizzato, ossia arrotondato al valore del profilo standard disponibile immediatamente superiore al valore trovato), scelgo finalmente i diversi profilati. Nel nostro caso, visti i valori irrisori di sforzo di trazione a cui sono sottoposte le aste, abbiamo dei valori di A_min che non superano 1,9cm²; possiamo quindi scegliere un unico profilato 33,7mm x 2,6mm (d x s) per tutte le aste tese.  

Infine, le aste compresse. Assumo i valori di f_yk e γ_m uguali a quelli utilizzati per le aste tese. Nell’inserire i valori dello sforzo Normale di compressione nelle tabelle, ne facciamo il modulo, così da renderli positivi. Nel caso delle aste compresse, come accennato prima, bisogna tener da conto anche il fenomeno dell’instabilità. Il valore di N non deve superare N_E, il carico critico euleriano , pari al prodotto

N_E = (π²*E*I_min)/(l_o²).

E rappresenta il modulo d’elasticità normale del materiale, pari a 210000 MPa, I_min il momento d’inerzia minimo della sezione, ossia l’asse lungo cui è più facile che il pilastro “svirgoli”, l_o la lunghezza minima d’inflessione, pari al prodotto tra l e β  (rispettivamente la lunghezza dell’asta – motivo per cui nella tabella Excel abbiamo mantenuto i valori dello sforzo Normale calcolati all’estremità dell’asta! – ed un coefficiente beta dipendente dai vincoli, nel nostro caso pari ad 1). E’ evidente che nel progetto di un’asta compressa ricerco un elevato valore di I_min ed un ridotto valore di l_o²(l_o*l_o). Introducendo il valore di ρ_min (il raggio d’inerzia minimo della sezione, una sorta di ellisse che rappresenta l’andamento dell’inerzia lungo la sezione), posso riscrivere I_min come il prodotto tra l’Area e ρ_min² ed introdurre la snellezza λ pari al rapporto tra l_o e ρ_min e riscrivere quindi l’equazione N_E tenendo conto di quest’ultimo valore. Senza adesso entrare eccessivamente nella discussione teorica ed allontanandoci così dal fine dell’esercitazione, ma anzi tornando al dimensionamento della travatura reticolare, risulta comunque evidente da questi pochi accenni come a fianco al valore dell’Area minima – nel caso dell’asta sottoposta a compressione – altrettanto fondamentale sia il valore del momento d’inerzia minimo.

Nel nostro caso, i valori di A_min non superano 3,8cm². I valori girano attorno a 2,1cm², 2,7cm², 3,5cm² e 3,8cm²…dovessimo tener da conto il solo valore dell’area minima, potremmo ipotizzare una struttura estremamente “performante” scegliendo tre profilati diversi: 33,7mm x 2,9mm, 42,4mm x 2,9mm e 42,4mm x 3,2mm.

Dobbiamo però tener da conto anche il momento d’inerzia. L’I_min della struttura analizzata variano dai 10cm⁴ ai 35cm⁴, passando per 14cm⁴, 19cm⁴, 22cm⁴, e 27cm⁴. Sceglieremo quindi dei profilati ben più grandi di quanto non avremmo fatto tenendo conto della sola area min. Giocando sempre al gioco utopistico della “struttura performante” portata all’estremo, sceglieremo quattro tipi di profilati: 48,3mm x 3,2mm, 60,3mm x 2,9mm, 60,3mm x 3,2mm e 76,1mm x 2,6mm.

Abbiamo così dimensionato la struttura reticolare spaziale. Potrei riassegnare le sezioni su SAP e mandare nuovamente l'analisi, ma sarebbe (quantomeno ai fini dell'esercitazione) un qualcosa di eccessivamente scrupoloso. Questo perchè, essendo le aste d'acciaio, non è necessario mandare novamente l'analisi tenendo da conto il peso della struttura (o meglio, essendo il peso piccolo rispetto ai carichi, lo si tiene indirettamente da conto nel momento dell'ingegnerizzazione immediatamente precedente la scelta del profilato).

1.Costrisco su Sap il modello di travatura reticolare spaziale con modulo quadrato 2x2.

2.Dispongo cerniere interne in tutti i nodi.

3-4.Assegno in 4 punti delle cerniere come vincolo esterno alla struttura (vista 2D e 3D).

5.Assegno i casi di carico -100 KN (nodi interni), -50KN (nodi esterni).

6.Deformazione della struttura

7.Grafico dello sforzo normale (verifico anche momento e taglio che dovrebbero essere pari a 0)

Procedo con il dimensionamento delle aste a sezione circolare della mia travatura reticolare spaziale, esporto la tabella con l'anilisi numerica per importarla su Excel.                                                                                                       Creo un nuovo file Excel con i dati numerici della mia struttura (calcolandomi con sap ache la lunghezza delle aste inclinate), e i dati presenti nel foglio Excel scaricato dal Portale di Meccanica (da L a Z).                                            A questo punto mi trovo una tabella divisa tra valori di sforzo normale  -/+ (aste compresse -) e (aste a trazione +). 

Utilizzo Tabelle di profilati metallici a sezione circolare forniti dal sito http://www.oppo.it/tabelle/profilati-tubi-circ.htm

Per le aste soggette a sforzo normale di compressione devo considerare i valori di A_{min e di} I_{min design} verificando che A_design  I_design  siano maggiori, e che il valore di snellezza non sia λ > 200.                                                           Per le aste soggette a sforzo normale di trazione considero solamente A_min che dovra essere minore della sezione metallica del profilato che scelgo (A_design).Il valore di λ deve essere anche qui inferiore a 200.

1. Costruisco una travatura reticolare spaziale su SAP costituita da piramidi rovesciate, controvettate, di dimensioni 2x2x2 sviluppata su una maglia ortogonale con modulo 8x6 .

2. Aggiungo  tramite l'operazione Define > Section Properties > Frame Section una nuova sezione, in questo caso Tubolare Cava (PIPE), rinominandola "asta", poichè questa sarà la sezione scelta per tutta la travatura reticolare.

3. Tramite il comando Assign > Frame > Frame Section assegno su tutta la struttura la sezione "asta" appena creata.

4.  Per trasformare i nodi delle aste in cerniere, bisogna effettuare il rilascio dei momenti tramite il comando Assign > Frame > Release/Partial fixity > Release, si spunta su Moment 22 e Moment 33 e nello start e nell’end inserisco i valori 0, rendendo libera la rotazione all’inizio e alla fine di ogni asta.

5. Inserisco le cerniere in modo casuale lungo il piano x,y, (aiutandomi con la vista 2d tramite View > Set View 2d (piano x,y  z=0) ) utilizzando il comando Assign > Joint > Restrain.

6. Assegno delle forze concentrate nei nodi strutturali. Creo prima la forza F : Define > Load Pattern  inserendo dove è scritto DEAD la lettera F e il valore 0 al posto di 1, clicco su Add New Load Pattern.

7. Seleziono la parte interna superiore della struttura, aiutandomi sempre con Set View 2d, ed eseguo il comando: Assign > Joint Loads > Forces assegnando la forza F precedente creata inserendo il valore -100 su Force Global Z. Successivamente seleziono il perimetro superiore della struttura inserendo una forza dimezzata di -50, poichè l'area di influenza dei nodi laterali perimetrali sono la metà dei nodi interni alla struttura. 

8. Inserite tutte le forze necessarie per l’Avvio dell’Analisi vado sul tasto Play (triangolo sulla toolbar) e seleziono prima DEAD e Modal dove imposto RUN/DO NOT RUN CASE, e dopodichè seleziono la forza F e clicco su Run NOW.

9. Adesso, per vedere cosa è successo alla mia struttura clicco prima su Show Deformed Shape (sempre sulla toolbar) e vedo la deformazione, poi su Show forces > Frame/Cables.. e vedo gli sforzi assiali lungo le aste reticolari.

10. Per visualizzare le tabelle con tutti i valori della struttura vado su : Display > Show Tables > Analysis Result. Spunto la casella Analysis Result. Vado su Select Load Pattern e seleziono la forza F. La tabella che a noi servirà sarà: Element Forces-Frames perchè fornisce il numero delle aste e le loro caratteristiche di sollecitazione a sforzo Normale.

11. Essendo questa struttura composta da aste di 3 lunghezza differente, creo 3 tabelle Excel differenti, ognuna la quale ha le sue rispettive misure in modo tale da sapere quale sforzo normale agisce su di essa. Per fare ciò vado su Select > Select > Select Lines Parallel To > Click Straight Line Objet e seleziono le aste con la stessa misura: per esempio, incomincio con le aste che misurano tutte 2 (aste dei rettangoli), poi 2,4495 (le diagonali delle piramidi) e infine 2,8284 (le diagonali dei rettangoli).

12.  Eseguo le stese operazioni per le tre diverse tabelle Excel ricavate dalla struttura :

1. Ordino i valori di Station, eliminando i valori diversi da 0.
2. Cancello i valori dopo la casella P (sforzo Normale).
3. Scrivo il dato L, lunghezza dell’asta in esame.

​​

13. Scaricata la tabella Excel fornita da questo sito, copio i dati che vanno dalla casella L in poi su un nuovo foglio Excel. Unifico i dati forniti da SAP e i dati della tabella scaricata. Ordino i valori di P (sforzo normale) dal più piccolo al più grande, in modo da avere aste compresse (valore negativo-blu) separate dalle aste in trazione (valore positivo-rosso). Sul dato N inserisco i valori del dato P tutti col segno positivo, per farlo inserisco la funzione: =E3*(-1) e la riporto fino a dove i valori di P sono negativi.

14. DATI:

      fyk  rappresenta la classe dell'Acciaio  scelta S235 e quindi il valore è 235 MPa per tutte le aste.

      γ_m  è il coefficiente di sicurezza e vale 1,05.

      β   è il coefficiente di vincolo e vale 1 perchè l'asta è vincolata da due                                      cerniere.

      E   è il modulo di elasticità dell'acciaio e vale 210000MPa.

      l   è la lunghezza delle aste e quindi avendole già riportate scrivo la                                       funzione =F3.

15. FORMULE: queste formule vanno scritte nel linguaggio Excel sotto i dati richiesti.

     f_yd = f_yk / γ_m          resistenza allo snervamento del materiale di progetto

     A_min= N / f_yd​          Area minima della sezione

     I_min= A_min x ρ²_min      momento di Inerzia minmo

      ρ_min= l₀ / λ*         raggio di Inerzia minimo

     λ*= π (E/f_yd)^1/2         coefficiente di snellezza massimo

     I_min, ρ_min,  λ*        questi valori sono importanti da calcolare nelle aste soggette a compressione ma                           no in quelle a trazione

16. SEZIONE: 

Per trovare le sezioni delle aste, vado sul sito http://www.oppo.it/tabelle/profilati-tubi-circ.htm  e trovo i valori di A_design, I_design  e  ρ_min  che li troviamo scritti sulla tabella OPPO su Sezione metallica, Momento di Inerzia e Modulo di Resistenza. Il Profilo corrisponde a dxs.

L'Area di design deve essere superiore all'Area minima e uguale per Inerzia di design che deve essere superiore all'Inerzia minima.

IMPORTANTE: il valore della snellezza λ non deve superare il valore 200.