SdC(b) (LM PA)

Il software SAP2000 permette di modellare in tre dimensioni una travatura reticolare spaziale e fornisce i dati utili al dimensionamento degli elementi che la compongono.

Dopo avere aperto un nuovo modello, per prima cosa bisogna assicurarsi che le unità di misura siano impostate su kN, m, c. Per iniziare a modellare i moduli bisogna impostare una griglia attraverso il comando Grid Only:

Nel mio caso ho impostato 7 linee lungo l'asse X, 2 linee lungo Y e 3 lungo Z, distanziate di 2m nelle direzioni di X e Y e di 1m in direzione Z.

Partendo dalla guida della griglia si procede quindi alla modellazione della prima campata che è composta da 6 moduli, dei quali quelli agli estremi sono prismi trapezoidali mentre quelli centrali sono cubi. 

Adesso possiamo reiterare lungo l'asse Y i moduli, giungendo quindi alla configurazione finale di 6x8 moduli (12x16m).

In questo passaggio bisogna fare attenzione alla posizione degli assi di riferimento rispetto al solido. in questo caso, volendo copiare gli elementi appartenenti alla selezione effettuata, andrà impostata una distanza di copia di -2 su Y, perchè orientata in senso opposto rispetto al sistema di coordinate riferimento.

A questo punto bisogna assegnare alla struttura appena modellata le caratteristiche di una travatura reticolare: bisogna cioè assegnare i vincoli: cerniere interne e cerniere esterne.

Per assegnare le cerniere esterne bisogna selezionare il nodo al quale si vuole assegnare questo tipo di vincolo e procedere con Assign > Joint > Restraints > e bloccare le traslazioni tutte le direzioni.

Per assegnare le cerniere interne bisogna assegnare ai nodi tra le travi un rilascio del momento, cioè un valore del momento nullo nelle connessioni tra le aste. Dopo aver selezionato tutti gli elementi: Assign > Frame > Release / Partial Fixity > Assegnare il rilascio del momento sia all'inizio che alla fine di ogni asta sia del momento 22 che del momento 33.

A questo punto bisogna assegnare i carichi. Dopo avere definito una nuova classe di carico da Define > Load Patterns, Bisogna creare un nuovo caso di carico (ad esempio F) che abbia come Self Weight Multiplier (moltiplicatore di peso proprio) il valore 0 (cioè che non aggiunga al carico stesso il peso proprio della struttura sulla quale agisce).

Per assegnare il carico si seleziona il nodo, Assign > Joint Loads > Forces (nelle travature reticolari il carico deve essere concentrato sui nodi, in modo che non ci siano nè taglio nè sforzo normale e la struttura lavori al meglio delle sue prestazioni) e si attribuisce un valore lungo Z espresso in kN, ma di segno negativo per indicare che graviti verso il basso.

A questo punto possiamo avviare l'analisi statico-lineare della struttura, selezionando soltanto l'analisi delle azioni dei carichi appartenenti al caso di carico F (deselezionando attraverso Do Not Run Case gli altri due casi, che restituiscono l'azione del peso proprio e un'analisi modale):

​Cliccando su Run Now ci viene infatti fornita in prima battuta una configurazione deformata:

In seconda battuta possiamo visualizzare i diagrammi delle sollecitazioni:

Display > Show Forces Stress > Frames / Cables > Axial

l'unico sforzo presente deve essere quello Assiale (sforzo normale) che viene rappresentato cromaticamente in blu se di trazione e in rosso se di compressione:

A questo punto abbiamo tutte le informazioni che ci servono per effettuare il dimensionamento di massima delle aste: Gli sforzi normali e la lunghezza delle aste, e scegliamo come materiale l'acciaio S235.

CTRL + T apre la finestra delle tabelle: a questo punto basta selezionare ANALYSIS RESULTS e selezionare il caso di carico F in Select Load Patterns.

Adesso possiamo esportare la nostra tabella riferita a Element Forces - Frames in Microsoft Excel. (Da File > Export)

A questo punto possiamo procedere con il dimensionamento delle aste che compongono la struttura. 

Per le Aste Tese basta calcolare l'area minima della sezione a partire dalla formula di Navier:

σ=N/A 

sapendo che la tensione σ non deve superare la tensione di snervamento fyd, ricaviamo la formula di progetto: 

Amin=N/fyd

Con un sagomario standard di tubi in acciaio a sezione circolare scegliamo ora profili che abbiano una sezione metallica maggiore dell'area minima:

Sono stati scelti 4 profili per le aste tese:

33,7 x 2,6 mm

42,4 x 2,6 mm

42,4 x 3,2 mm

60,3 x 2,9 mm

Per il dimensionamento delle aste compresse si segue un procedimento diverso, infatti in questo caso bisogna tener conto del carico critico euleriano, quindi prendere in considerazione parametri come la lunghezza dell'elemento, la tipologia dei vincoli e il materiale (modulo di elasticità e resistenza), per calcolare l'inerzia minima e il raggio d'inerzia minimo.

Come prima cosa inserisco nella tabella i dati:

scelgo il materiale: Acciaio S235 

specifiche:

modulo di elasticità E= 210.000 MPa

resistenza caratteristica allo snervamento fyk= 235 MPa

coefficiente di sicurezza γm= 1,05

il coefficiente β è dato dal tipo di vincolo di ogni elemento: in questo caso abbiamo aste incernierate a entrambe le estremità quindi il valore β è 1.

Il valore degli sforzi Normali ci viene fornito da SAP, dobbiamo prendere in considerazione nel caso degli N di compressione il valore assoluto (creiamo una nuova colonna e moltiplichiamo ogni valore dello sforzo assiale di compressione per -1).

Adesso possiamo calcolare la resistenza di progetto:

 

fyd=fyk/γm

L'area minima:

Amin=N/fyd

La snellezza critica:

λ*=π√E/fyd

Il raggio d'inerzia minimo:

ρmin= β x l / λ*

Il momento d'inerzia minimo:

Imin=Amin x ρmin^2

Con quest'ultimo Valore scegliamo un profilo dal sagomario che abbia un momento d'inerzia maggiore, facendo comunque attenzione che anche l'area del profilo scelto non sia inferiore all'area minima. 

E infine la snellezza:

λ= β*l*/ρmin (design)

che deve essere inferiore a 200.

Sono stati scelti 7 profili per le aste compresse, di cui 3 in comune con quelle tese:

33,7 x 2,6 mm

42,4 x 2,6 mm

48,3 x 2,6 mm

60,3 x 2,9 mm

76,1 x 2,6 mm

88,9 x 2,6 mm

88,9 x 3,6 mm

 

 

 

 

 

 

 

 

 

 

 

In questa prima esercitazione l'obiettivo era un primo dimensionamento di una travatura reticolare spaziale attraverso il programma SAP2000 e tabelle Excel.

Per iniziare ho creato un nuovo file su SAP scegliendo come unità di misura kN, m, C e una griglia che avesse lati x, y e z pari a 2m per creare il primo modulo della mia trave reticolare spaziale.

 

 

 

 

 

 

 

 

 

 

 

 

Creato il primo modulo 2mx2mx2m, selezionando tutto il blocco tranne una sua faccia lo ho copiato più volte a distanza 2m, 4m, 6m etc.. lungo l'asse y arrivando ad una lunghezza totale di 12m. Selezionando ora il nuovo blocco, allo stesso modo del precedente, lo ho copiato lungo l'asse x arrivando anche qui a 12m, creando così una trave reticolare spaziale 12mx12m.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Essendo una trave reticolare tutte le intersezioni delle aste devono essere dei nodi a cerniera, dunque ho selezionato tutta la trave e andando su Assign-Frame-Releases/Partial Fixity ho rimosso i vincoli riguardanti il Momento (Moment 22 e Moment 33) ad inizio e fine di agni asta.

  

 

 

 

 

 

 

Dopodichè mi sono posizionato in vista 2d sul piano z=0 ed ho selezionato i punti dove intendevo sono andato a piazzare delle cerniere andando su Assign-Joint-Restraints

 

 

 

 

 

 

Per posizionare invece le forze concentrate su ogni nodo mi sono posto sul piano 2d z=2 in modo da poter selezionare facilmente solo i nodi sul piano superiore, una volta selezionati tutti i nodi interni ho assegnato loro una forza concentrata pari a 100 kN, invece sui nodi di bordo, avendo metà area di influenza rispetto agli altri, 50kN. Tutto questo andando su Assign-Joint Loads-Forces e crando un nuovo tipo di Load Pattern da me chimato F che non consideri il peso proprio

 

 

 

 

 

 

 

 

 

 

 

 

 

Una volta assegnati tutti i carichi ho specificato il tipo di sezione, selezionando tutta la trave reticolare e andando su Define-Section Properties-Frame Section, specificando che sono dei tubolari.

 

 

 

 

 

inoltre ho assegnato ad ogni tubolare solo 2 Output Stations in modo da non avere troppi valori superflui in tabella, andando su Assign-Frame-Output Stations e ponendo 1 come valore in Min Number Stations.

 

 

 

 

 

 

Fatto questo ho fatto partire l'analisi, lanciando solo F come caso e ho visto i valori di sforzo normale a cui la mia reticolare era sottoposta.

 

Data una rapida occhiata agli sforzi a cui è sottoposta la trave sono andandato su Display-Show Tables per ottenere una tabella di tutti gli sforzi su ogni tubolare e l'ho esportata su Excel.

 

 

 

 

 

Eliminati i valori doppi di ogni tubolare li ho ordinati dal valore minore al maggiore e dopo ho trasferito il numero di asta assegnato da sap e i valori dello sforzo normale su una tabella excel, scaricata appositamente dal sito di portale di meccanica, nella sezione accaiaio, accuratamente modificata, indicandoli con Frame e P ponendo poi come funzione per la colonna delle N il valore assoluto degli sforzi trovati P.

 

 

 

 

 

Avendo tutti gli sforzi normali con valore assoluto ho iniziato a dimensionare i tubolari usando un'acciaio S275 (quindi ho posto nella colonna dell'fyk, ovvero la tensione caratteristica di progetto, il valore di 275MPa e nella colonna del γ_m, ovvero il coefficente di sicurezza, 1,05). Inoltre ho posto come valore del coefficente di vincolo di ogni tubolare β=1, essendo incernierati su entrambi i lati, il valore del modulo di elasticità dell'acciaio E=210000MPa e la lunghezza di ogni tubolare l preso dalla precedente tabella.

Grazie alle funzioni preimpostate la tabella ha calcolato in automatico f_yd = f_yk / γ_m e dunque l'Area minima della sezione  A_min= N / f_yd.

Grazie al valore dell'Area minima ho potuto dimensionare tutti i tubolari soggetti a trazione andando a scegliere un profilato esistente con Area di sezione maggiore o uguale dell'Area minima, inserendo poi i valori dell'asta di progetto nelle colonne A_design (per l'Area), I_design (per il momento d'inerzia) e ρ_design (per il raggio d'inerzia).

 

 

 

 

 

 

 

 

 

 

Questi ultimi due valori non erano particolarmente rilevanti per il dimensionamento a trazione, ma sono fondamentali per il dimensionamento a compressione per controllare che l'asta non abbia problemi di instabilità: infatti nel dimensionare i tubolari compressi, oltre a prendere un profilato che avesse Area di sezione maggiore o uguale dell'Area minima ho anche controllato che ognuno avesse un Momento d'inerzia (I_design) ed un raggio d'inerzia (ρ_design) maggiore rispettivamente del Momento d'inerzia minimo (I_min calcolato sempre dalla tabella grazie alla funzione I_min= A_min x ρ²_min) e del raggio d'inerzia minimo (ρ_min che si trova dalla funzione ρ_min= l₀ / λ*, con l₀ che è la lunghezza libera d'inflessione ed è uguale ad l x β = l essendo β=1 e λ* che è il coefficente di snellezza massimo che è uguale a λ*= π (E/f_yd)^1/2 ).

Ovviamente non si può pensare di dimensionare un tubolare per ogni Area minima o Momento d'inerzia e raggio d'inerzia minima, poichè troveremmo un numero spropositato di aste diverse e non sarebbe pratico. Dunque ho scelto 7 tubolari tipo in modo da non avere troppe sezioni diverse e allo stesso tempo evitare eccessivi sovradimensionamenti.

Una volta fatto questo primo dimensionamento dovrei assegnare ad ogni frame su SAP il tubolare da me scelto, con il peso proprio, e rimandare l'analisi e rianalizzare gli sforzi.

 

 

Modellazione con SAP 2000: File-New Model-Grid Only,inserendo le unità di misura con cui voglio lavorare[KN,m,C°]
Nella finestra Quick Grid Lines inserisco il numero delle griglie su cui imposto il mio disegno nelle tre direzioni (Number of Grid Lines), e la spaziatura che voglio fra le linee della griglia (Grid Spacing) creando una sola campata:

                       

Con Draw Frame costruisco la prima campata reticolare cubica. Dopodichè me la copio e incollo con Ctrl+C e Ctrl+V lungo gli assi x e y finchè non realizzo la struttura reticolare desiderata:

Il 6 indica la distanza del punto di ancoraggio della nuova campata rispetto all'origine degli assi, che è uguale alla profondità della prima campata.

VINCOLI ESTERNI:seleziono quattro nodi a caso della struttura (ma che non siano allineati) e gli assegno una cerniera: Assign-Joint-Restraints-Icona della cerniera:

                                                 

 

VINCOLI INTERNI:rendo tutti i nodi cerniere interne, quindi seleziono tutta la struttura e poi Assign-Frame-Releases-Partial Fixity e spunto Moment 2-2 e 3-3 sia su Start che su End:

MATERIALE E PROFILO:Seleziono la struttura, poi Assign-Frame-Frame Sections-Add New Property-Pipe e la nomino "asta":

CARICO CONCENTRATO:creo il carico puntiforme " f " (Define-Load Patterns-Load Pattern " f "-Self Weight Multiplier " 0 " (lo privo di peso proprio)-Add New Load Pattern-Seleziono " f ". Assegno il carico selezionando la parte terminale superiore della struttura e procedendo poi con Assign-Joint-Joint Loads-Forces- "f"-Force Global z (asse lungo la quale si troverà "f" )- Inserisco il valore del carico " - 150 KN " (negativo perchè è diretto nel verso opposto all'asse z):

N.B.: Ai nodi perimetrali della struttura verrà assegnato un carico che corrisponde alla metà del carico assegnato ai nodi centrali della struttura,poichè i carichi agiscono su una superficie intorno al nodo che corrisponde alla metà della superficie nella quale i carichi agiscono sui nodi centrali.

Analisi: analizzo la struttura (Run Analysis), facendo "correre" (Run) solo i miei carichi concentrati:

DEFORMATA                                                                          DIAGRAMMA SFORZO  NORMALE

N.B.: I diagrammi del Taglio e del Momento devono equivalere a zero.

Dimensionamento: Abbiamo bisogno di conoscere il valore dello sforzo normale di ogni singola asta:

- Creo da SAP una tabella che mi mostri questi valori ( Display-Show Tables-Analysis Results-Select Load Patterns " f "-Select Load Cases " f ").

- Seleziono dal menù a tendina laterale Element Forces-Frames.

- Lo esporto in Excel ( File-Export Current Table-to Excel).

Ripulisco il file dai valori che non mi servono, lasciando i valori relativi alle numerazioni e alle luci delle aste, allo sforzo normale e ai carichi concentrati applicati, e ordino in modo crescente la luce delle aste per conservare solo la lunghezza delle aste normali L (che è uguale a 6 m ) e la lunghezza delle aste diagonali (che è uguale a L moltiplicato per la radice di 2 = 6* radice di 2 = 8,49 m ).

Se ordino anche lo sforzo normale distinguo tra aste compresse e aste tese.

Trazione: Inserisco i valori di N superiori allo zero (trazione) nel file Excel creato per il dimensionamento:

- Scelgo un acciaio (S235, acciao molto duttile, buono per prestazioni antisismiche) dalla quale dovrò prendere il coefficiente di snervamento fgk (= 275 Mpa) e il coefficiente di sicurezza ym (= 1,05) e da questi dati dovrò trovare la tensione di progetto fd attraverso la formula fd=fgk/ym e poi l'Area minima di progetto A_min con la formula A_min= N/fd

Il valora A_min va ingegnerizzato,cioè va preso il profilo standard disponibile immediatamente superiore al valore da me trovato.

Compressione: Inserisco i valori di N inferiori allo zero (compressione) nel file Excel omettendo il segno " meno" ai fini del calcolo strutturale:

- Assumo i valori di fyk e ym uguali a quelli utilizzati per la trazione.

- Oltre ai valori di fd e A_min dovrò ricavarmi anche i valori dell' Inerzia minima I_min, il raggio di inerzia minimo della sezione rho_min e la snellezza massima dell'asta lambda*, assumendo come dati anche il Modulo di Elasticità E (=210000 Mpa) e un coefficiente beta che dipende dalle condizioni di vincolo (nel nostro caso=1). Dovrò dunque ingegnerizzare i risultati trovati, individuandoli nella tabella dei profili standard:

 

 

 

 

 

 

L'obiettivo dell'esercitazione è il disegno, l'analisi dei carichi e il dimensionamento delle aste di una struttura a carattere reticolare. In questo caso, ho deciso di concepire una piastra di copertura su 4 appoggi, con un buco centrale per un patio, costituita da moduli quadrati di 1,5 m di lato, per un totale di 12x8 moduli.

Comincio disegnando la piastra su SAP2000 su una griglia 1,5x1,5x1,5, partendo dal modulo singolo e copiandolo nelle due direzioni:

pongo i vincoli di cerniera interna (Assign->Frames->Releases/Partial Fixities; sblocco la rotazione):

Assegno le 4 cerniere esterne (Assign->Restraints; scelgo la cerniera):

"Simulando" un'analisi dei carichi, individuo i nodi più sollecitati (100 KN), i nodi di bordo (50 KN), i nodi al vertice (25 KN) e i nodi ai vertici del patio (75 KN) e li applico dopo aver configurato una forza puntuale verticale verso il basso "F" (Assign->Joint Loads):

A questo punto effettuo l'analisi delle sollecitazioni (essendo una reticolare troverò solo sforzo normale) (Run Analysis; considero solo gli effetti delle F; Show); noto che le aste maggiormente sollecitate sono quelle in corrispondenza dei vincoli esterni:

Mi assicuro che nella tabella di analisi mi venga riportato un solo valore per ogni asta (lo sforzo assiale è costante!)

E visualizzo la tabella (Display->Show Tables):

E la esporto in formato Excel:

Elimino i doppioni analizzando solo un caso per ogni asta (ricordiamo che lo sforzo normale è costante):

Dopo aver scaricato la tabella Excel fornita dal Corso, rimuovo le caselle non necessarie:

E inserisco i valori  della normale risultati dall'analisi, in ordine crescente:

Inserisco un'ulteriore casella dove visualizzo solo il valore assoluto dello sforzo normale, necessario affinché si possa eseguire il dimensionamento:

Scelgo un materiale (acciaio S275) e pongo le costanti (tensione di rottura e gamma di sicurezza):

Conosco anche il modulo d'elasticità, la lunghezza delle aste e il coefficiente della tipologia di vincolo (beta):

Per le aste tese (non soggette ad insabilità) non considero valori come la lunghezza e il beta:

Inizio a dimensionare le aste compresse trovando dei profili tubolari adeguati dal sagomario, tenendo da conto l'area minima trovata dal rapporto tra normale e tensione di progetto, e assicurandomi che il profilo scelto abbia anche adeguati valori di momento d'inerzia e raggio d'inerzia calcolati dalle funzioni inserite nel foglio Excel:

e continuo così:

Per le aste tese considero solo l'area minima:

La struttura così progettata necessiterà in totale di 8 tipi diversi di profili; questo dipende dall'economicizzare il numero di tipi di profili a scapito di avere alcuni elementi molto sovradimensionati.

1. Realizzo la struttura e assegno la sezione circolare a tutte le travi 
2. Assegno le cerniere interne a tutti i nodi 
3. Dispongo 5 cerniere esterne 
4. Assegno delle forze concentrate interne alla struttura (-200 KN) ed esterne (-100 KN) 
5. Procedo con la verifica della deformazione della struttura attraverso il comando "Run now": è assente il momento ma presente lo sforzo assiale 
6. Esporto la Tabella "Element Forces Frame" su Excel 
7. Creo una nuova tabella Excel con all'interno i dati della mia struttura ed i dati presenti nel foglio Excel scaricato dal Portale di Meccanica (da L a Z) 
8. Prima di iniziare con l'inserimento dei dati, calcolo quanto misurano le aste diagonali della struttura; quindi le analizzo con SAP e importo i dati nel foglio Excel
9. Inizio la compilazione della tabella partendo dalle aste soggette a compressione (sforzo normale negativo); utilizzo il sito  http://www.oppo.it/, che mette a disposizione Tabelle di profilati metallici a sezione circolare. Prendo in considerazione i dati nei riquadri rossi 
10. Inserisco i valori delle tabelle oppo nelle colonne Adesign, Idesign e ῤminimo che corrispondono alla sezione metallica, al momento d'Inerzia ed al raggio di'inerzia, così da trovarmi il valore λ che indica la snellezza del profilato (non deve essere inferiore a 200). Faccio attenzione che il momento d'inerzia e l'area del profilato siano maggiori del Momento d'inerzia minimo e dell'Area minima dell'asta. Di conseguenza scelgo il profilato più adatto 
11. Per le aste tese a trazione il procedimento è simile a quello per le aste tese a compressione ma questa volta non mi interesso più dell'Inerzia minima ma solo dell'Area minima che deve essere sempre minore della sezione metallica del mio profilato 

In allegato: file SAP e foglio Excel

SAP2000

1 PASSAGGIO:  REALIZZO LA STRUTTURA AD L A PARTIRE DA UN UNICO VOLUME E ASSEGNO LA SEZIONE CIRCOLARE A TUTTE LE TRAVI.

2 PASSAGGIO: ASSEGNO TUTTE LE CERNIERE A TUTTI I NODI.

3 PASSAGGIO: ASSEGNO LE CERNIERE ESTERNE.

4 PASSAGGIO: ASSEGNO LE FORZE INTERNE -200 (KN) E QUELLE ESTERNE -100 (KN) (LA METÀ DELLE INTERNE).

5 PASSAGGIO: ATTRAVERSO RUN NOW VERIFICO LA DEFORMAZIONE DELLA STRUTTURA.

6-6a PASSAGGIO: VERIFICO CON LA TORSIONE CHE NON HO MOMENTO E CON LE AXIAL FORCES CHE HO SPOSTAMENTO VERTICALE.

7 PASSAGGIO: ESPORTO LA TABELLA “ELEMENT FORCES-FRAME” SU EXCEL.

EXCEL

8 PASSAGGIO: ORDINO “STATION” DAL PIÙ PICCOLO AL PIÙ GRANDE E ELIMINO TUTTI I VALORI DOPO LO ZERO.

9 PASSAGGIO: CREO UN FOGLIO EXCEL CON I DATI OTTENUTI DALL’ESPORTAZIONE, UNITI AI DATI PRESENTI NEL FOGLIO EXCEL SCARICATO DAL PORTALE.

10 PASSAGGIO: COMPILO LA TABELLA TENENDO CONTO DEL FATTO CHE HO ASTE SOGGETTE A COMPRESSIONE (P=SFORZO NORMALE NEGATIVO) E ASTE SOGGETTE A TRAZIONE (P POSITIVO), EVIDENZIATE IN GIALLO, E CHE INOLTRE LE ASTE HANNO LUNNGHEZZA ALCUNE 2m, ALTRE (LE DIAGONALI) 2,82m, EVIDENZIATE IN ROSSO. UTILIZZO LE TABELLE PRESE DA http://www.oppo.it/tabelle/profilati-tubi-circ.htm RELATIVE AI TUBI IN ACCIAIO A SEZIONE CIRCOLARE, (EVIDENZIATE IN ROSSO).

 

 

 

11 PASSAGGIO: INIZIO DALLE ASTE COMPRESSE. INSERISCO I VALORI Adesign, Idesign E ρmin CHE TROVO NELLE TEBELLE DI OPPO, CHE CORRISPONDO RISPETTIVAMENTE A SEZIONE METALLICA, MOMENTO D’INERZIA E RAGGIO D’INERZIA. QUESTI DEVONO ESSERE SUPERIORI AI VALORI DI Amin E Imin CHE HO IO NELLA MIA TABELLA EXCEL. DEVO OTTENERE UNA SNELLEZZA λ SEMPRE INFERIORE A 200, (EVIDENZIATA IN BLU). 

 

 

12 PASSAGGIO: CONTINUO CON LE ASTE TESE. INSERISCO I VALORI Adesign, Idesign E ρmin CHE TROVO NELLE TEBELLE DI OPPO, TENENDO CONTO CHE Adesign DEVE ESSERE MAGGIORE DELLA Amin. ANCHE QUI DEVO OTTENERE UNA SNELLEZZA λ SEMPRE INFERIORE A 200, (EVIDENZIATA IN BLU).

IN ALLEGATO HO INSERITO IL FILE SAP2000 E IL FILE EXCEL

 

 

 

 

 

 

 

Dimensiono una travatura reticolare triangolare partendo dal modello di griglia semplice che mi fornisce il programma SAP, decidendo il numero di campate e i metri di ogni campata nelle direzioni X,Y e Z.

 

• Disegno la campata di base e la copio e incollo (cmd. COPY e PASTE) riempiendo tutta la griglia. Attivo lo snap middle point e con un offset dato dalla metà della griglia riesco a creare il vertice della piramide.

• Posiziono tre cerniere esterne nel modello nei nodi, e rilascio tutti i momenti sia in asse 2,2 che in asse 3,3 di ogni cerniera.
• Assegno delle forze esterne: alla trave reticolare sono appesi 8 solai da 10 kN/m². Nella parte esterna della trave avrò una forza pari a -80 kN, nella parte interna una forces pari ala metà, -40kN.

• Avvio l'analisi della struttura per trovare la deformata e i diagrammi del solo sforzo normale sulle singole aste.
  Poichè si tratta di una travatura reticolare, le aste verrano sollecitate solo con axial forces (di compressione o trazione) e i loro momenti risulteranno zero.

• A questo punto esporto le tabelle in excell, e facendo riferimento al foglio elettronico dato attraverso la sezione download del portale di meccanica di Roma tre, costruisco un foglio elettronico.
• Copio nella casella delle forze il valore dello sforzo assiale di ogni singola asta esportando a blocchi: prima le aste lunghe 5m, posizionate lungo i quadrati, poi le aste lunghe 4.04m di collegamento tra il quadrato e la punta della piramide ed infine le aste lunghe 7,07m controventamenti dei quadrati della travatura reticolare.

ESPORTAZIONI DEGLI SPIGOLI DELLA PIRAMIDE

• Dopo di che divido il file excell in 2 parti, una riguardante sforzo normale di compressione in rosso e una di trazione in blu.

• Tratto i due fogli in maniera diversa: per quanto riguarda le aste soggette a sforzo normale di compressione, ingegnerizzo l’ area e momento di inerzia facendo attenzione a non superare di 200 la Lamba di progetto per superare l’ istabilità euleriana. Per quanto riguarda le aste soggette a sforzo di trazione invece, non tengo conto del fenomeno euleriano, ma prendo in considerazione solo l’ area di progetto
• Per la scelta del profilo adatto a soddisfare le condizioni minime di Area e momento di inezia, ho preso di riferimento la tabella dei profilati cavi scaricato dal sito di Oppo - http://www.oppo.it/tabelle/profilati-tubi-circ.htm

 

in allegato il foglio di calcolo finale e file .sdb

---

La struttura analizzata è una superficie rigata a curvatura negativa definita come “paraboloide iperbolico”. Si è voluta scegliere poichè io ed il mio collega, Valerio Minella, l’abbiamo studiata, calcolata e costruita nel corso singolo “Geometrie e Modelli” delle professoresse Tedeschini Lalli-Magrone. Avevamo quindi il desiderio di capirne il funzionamento con la natura di reticolare spaziale.

Vorrei premettere da subito che io ed il mio collega abbiamo realizzato 2 modelli di paraboloide iperbolico completamente differenti l’uno dall’altro.

Il mio modello è stato realizzato in Rhinoceros grazie all’utilizzo di 4 “rette sghembe” che fungono da direttrici della superficie descritta da un insieme finito di rette che. Ovviamente, il mio modello è un’approssimazione della superficie : sia perchè avranno un certo spessore quando gli assegnerò una sezione, sia perchè il loro numero è tutt’altro che infinito.

                      

 

Passo 1: Esporto il file nel formato.dxf e lo importo su SAP2000 (non c’è stato bisogno di passare per AutoCAD perchè Rhinoceros esporta già di suo i .dxf del 2004). Ovviemente ho fatto in modo che il modello si trovi sull’origine degli assi (0,0,0) e che abbia come asse veticale l’asse z.

 

 

Passo 2: Una volta inserito selezione tutti i frame del modello è gli assegno delle cerniere interne con il rilascio dei momenti sulle tre dimensioni dandogli così comportamento di reticolare spaziale.

 

   

 

Passo 3: Si passa poi all’asssegnazione dei vincoli esterni, “cerniere”, in maniera arbitraria sui nodi alla base del modello. Per far ciò sono dovuto rimanere sulla visualizzazione 3d poichè SAP2000 lavora sulla visualizzazione 2d dei piani.

 

   

Passo 4: Mi semplfico le tabelle finali selezionando tutti i frame del modello e assegnandogli un valore minimo di Stazioni pari ad 1: questo farà in modo che le tabelle delle analisi finali sulle sollecitazioni interne avranno solamente un valore all’inizio e alla fine asta, poichè essendo una reticlore spaziale avrà solamente sforzo Normale Costante.

 

 

Passo 5: Assegno a tutti i frame la sezione tubolare cava in avviaio di default di SAP2000

 

 

Passo 6: Successivamente passo all’assegnazione dei carichi sulla struttura: seleziono, sempre mediante la visulizzazione 3d, tutti i i nodi della superficie superiore, tranne quelli al bordo, è gli assegno una forza F, senza peso proprio, di direzione –z e di valore 100 kN, ai restanti nodi al bordo assegno la forza F sempre in direzione –z  con valore dimezzato, cioè 50 kN, questo perchè, essendo la natura del carico è distribuita, l’area di influenza dei nodi ai bordi è minore o uguale alla metà.

 

     

Passo 7: A questo punto sono pronto per avviare l’analisi della struttura e appare subito lo schema della deformata.

 

  

 

Passo 8: 

Controllo subito se c’è sforzo di Taglio o Momento flettente nella struttura: se ciò accadesse vuol dire che c’è stato un errore nella modellazione della struttura o nell’inserimento delle cerniere interne. Il risultato è positivo poichè i valori non esistono.

Controllo il diagramma dello sforzo Normale (il valore in rosso è di compressione, quello in blu di trazione).

 

  

 

Passo 9: L’ultimo lavoro che facciamo con SAP2000 è quello di farci tabellare in valori delle solecitazioni interne (in questo caso solo sforzo Normale). A questo punto esportiamo la tabella in excel e lasciamo SAP2000.

 

 

Passo 10: Prendendo spunti dalla tabella esportata da SAP2000 e dalla tabella esercitazione_pilastri.xls nel materiale scaricabile sul sito, realizzo uno file excel con 2 schede, una per aste compresse ed una per aste tese.

Passo 11: 

Inserisco, per le aste compresse, il valore dello sforzo normale di compressione (rendendolo positivo) e la lunghezza libera d’inflessione di ogni frame: quest’ultima sarà uguale alla lunghezza di dell’asta stessa poichè, avendo come vincoli agli estremi 2 cerniere, ha un coefficente di vicolo β pari ad 1.

 

                               _l0 = β l                                                                     (1)

                               _l0 = l                                                                        (2)

 

Passo 11: Specifico che voglio utilizzare un acciaio S235 andando ad inserire la tensione caratteristica di progetto f_yk ed il coefficente di sicurezza γ_m pari a 1,05. Grazie a questi due valori mi trovo la resistenza di progetto f_yd (3).Succesivamente trovo l’area minima A_min della sezione grazie alla formula di Saint Venant (4).

 

                               _fyd = f_yk / γ_m                                                                   (3)

                               A_min= N / f_yd                                                                   (4)

 

Passo 12:  Inserisco il modulo dei elasticità E dell’acciaio in modo tale che posso trovarmi la massima snellezza λ* possiblie che la trave compressa deve avere affinche l’instabilità non si inneschi prima dello schiacciamento (5). Da questa ci ricaviamo automaticamente il raggio d’inerzia minimo ρ_min (6) e, successivamente, il momento d’Inerzia minimo I_min (7).

 

                               λ*= π (E/f_yd)^1/2                                                              (5)

                               ρ_min= l₀ / λ*                                                                   (6)

                              I_min= A_min  ρ²_min                                                             (7)

 

Passo 13: Trovati A_min e I_min andiamo a prendere il sagomario dei profilati mettalici a sezione circolare cava dal sito www.oppo.it ed iniziamo ad assegnare le sezioni che abbiano un valore superiore a tutti e 2 (attenzione, l’Area da prendere in considerazione è l’area della sezione metallica). Scelto il profilato da assegnare scrivo i nuovi valori di Area A_design Momento d’Inerzia I_design e raggio d’inerzia ρ_design in modo tale da ricalcolarmi la snellezza λ, da normativa tale valore deve essere inferiore a 200 (coefficiente adimensionale poichè la snellezza è il rapporto di due lunghezze).

 

 

Passo 13: Ripeto lo stesso procedimento per le aste in acciao tese fermandomi all’Area minima poichè l’acciao teso non ha problemi di instabiltà.

 

 

Il passo successivo sarà quello di riassegnare le sezioni su SAP2000 e rimandare l’analisi.

La struttura analizzata è una superficie rigata a curvatura negativa definita come “paraboloide iperbolico”. Si è voluta scegliere poiché io ed il mio collega, Tommaso Passerini, l’abbiamo studiata, calcolata e costruita nel corso singolo “Geometrie e Modelli” delle professoresse Tedeschini Lalli-Magrone e perché avevamo il desiderio di capirne il funzionamento con la natura di reticolare spaziale. Vorrei premettere da subito che io ed il mio collega abbiamo realizzato 2 modelli di paraboloide iperbolico completamente differenti l’uno dall’altro.

---

La modellazione della superficie è stata affrontata con AutoCAD tramite una costruzione spaziale di “frame spezzati” che consentivano una giusta importazione nel software di calcolo SAP 2000.

La costruzione ha seguito un iter compositivo basato sulla realizzazione di 4 aste sghembe “perimetrali” della superficie a base quadrata sul quale poi sono state costruite per punti tutte le “rigate”, partendo da un’asta base di 2m di lunghezza.

  

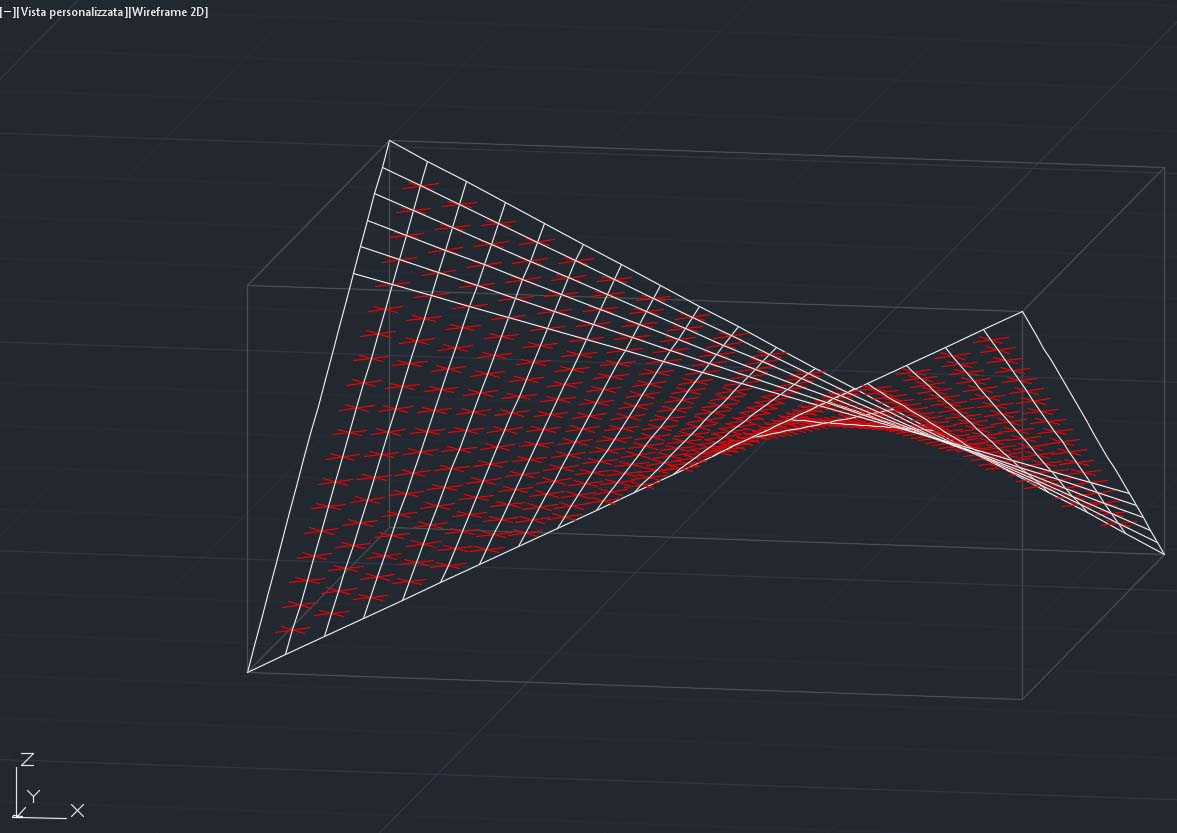
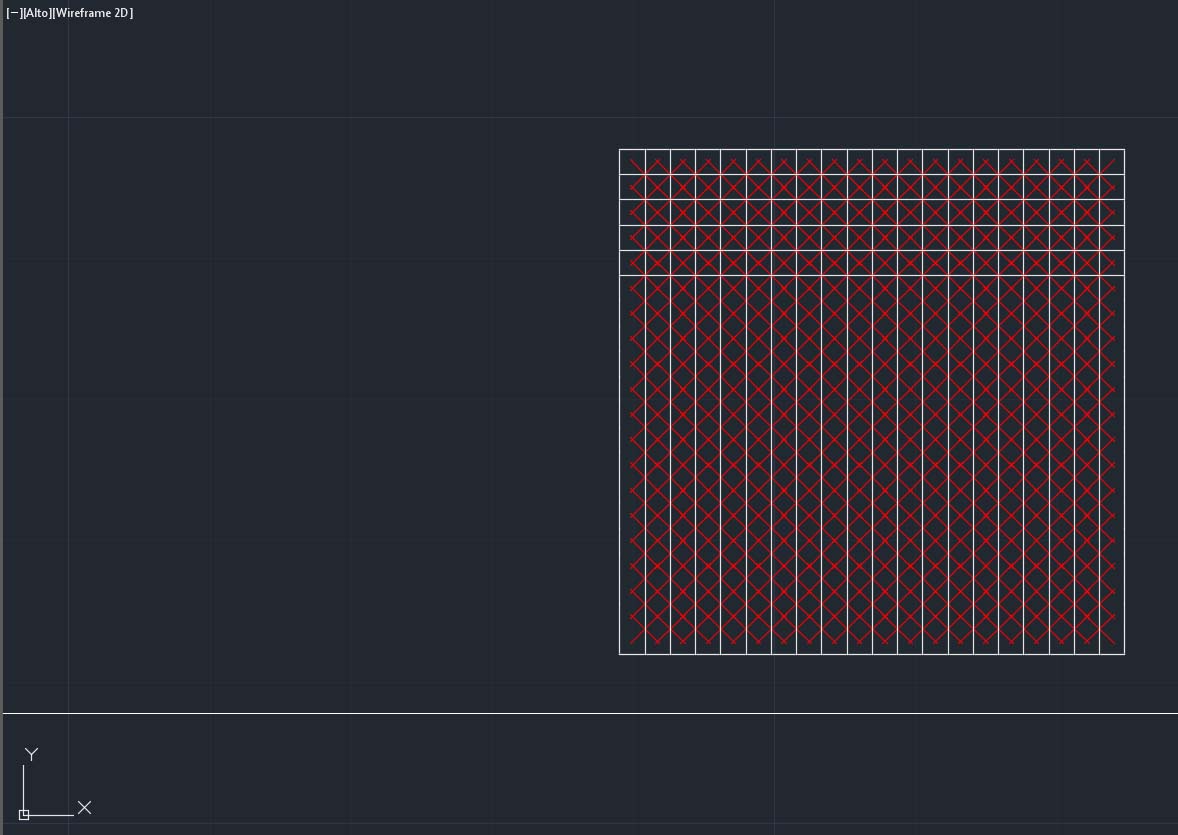
Scelta una curvatura appropriata a definire una superficie tridimensionale idonea al calcolo delle sollecitazioni, sono stati costruiti (uno ad uno) tutti i frame necessari per comporre una travatura che esprimesse il compito di reticolare.

  

  

  

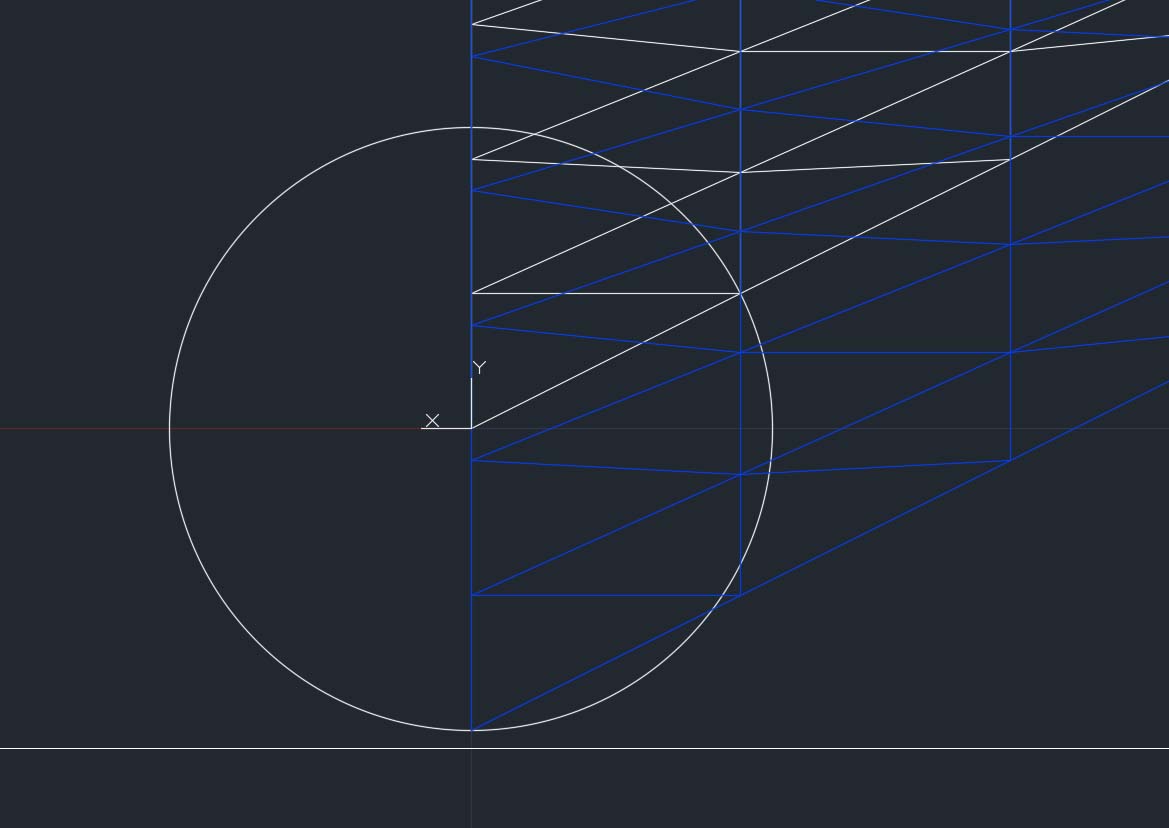
Effettuando gli opportuni accorgimenti di importazione tra diversi software (centramento del modello nell’origine degli assi del foglio di lavoro, ribaltamento del modello sull’asse XZ, copia del modello su layer appropriato e esportazione come file .dxf), il modello è stato lavorato in SAP 2000 come descrivono i passaggi successivi.

  

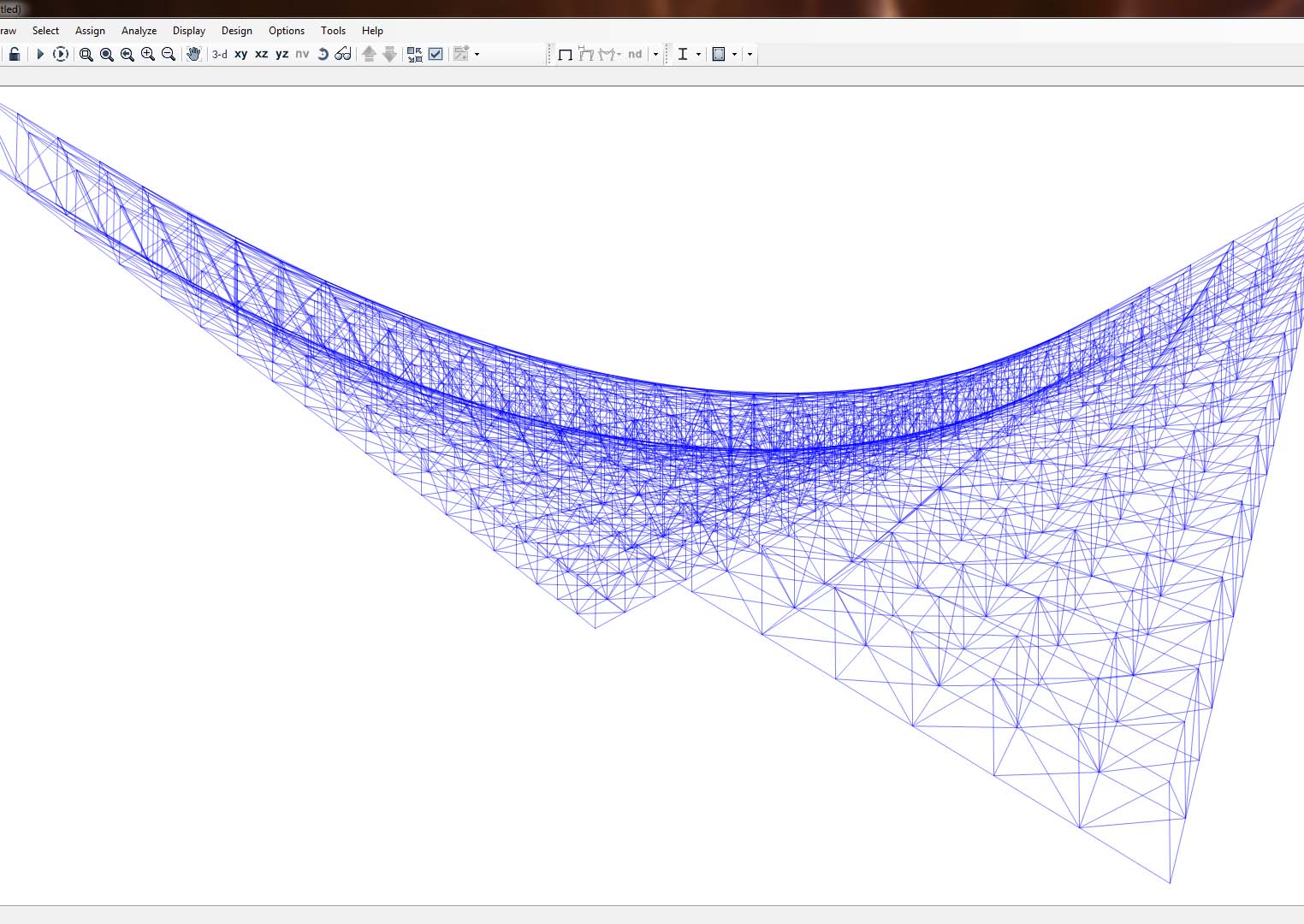
Step-1: selezione di tutti i frame del modello e impostazione di calcolo della deformata e delle sollecitazioni solo in due Output Station ai due estremi dell’asta, poiché essendo una travatura reticolare spaziale sarà soggetta solo a sforzi normali COSTANTI e quindi definibili attraverso un solo valore di questo su qualsiasi punto dell’asta, inoltre poiché per il dimensionamento di massima occorre avere la lunghezza di ogni frame si decide di impostare il secondo Output Station;

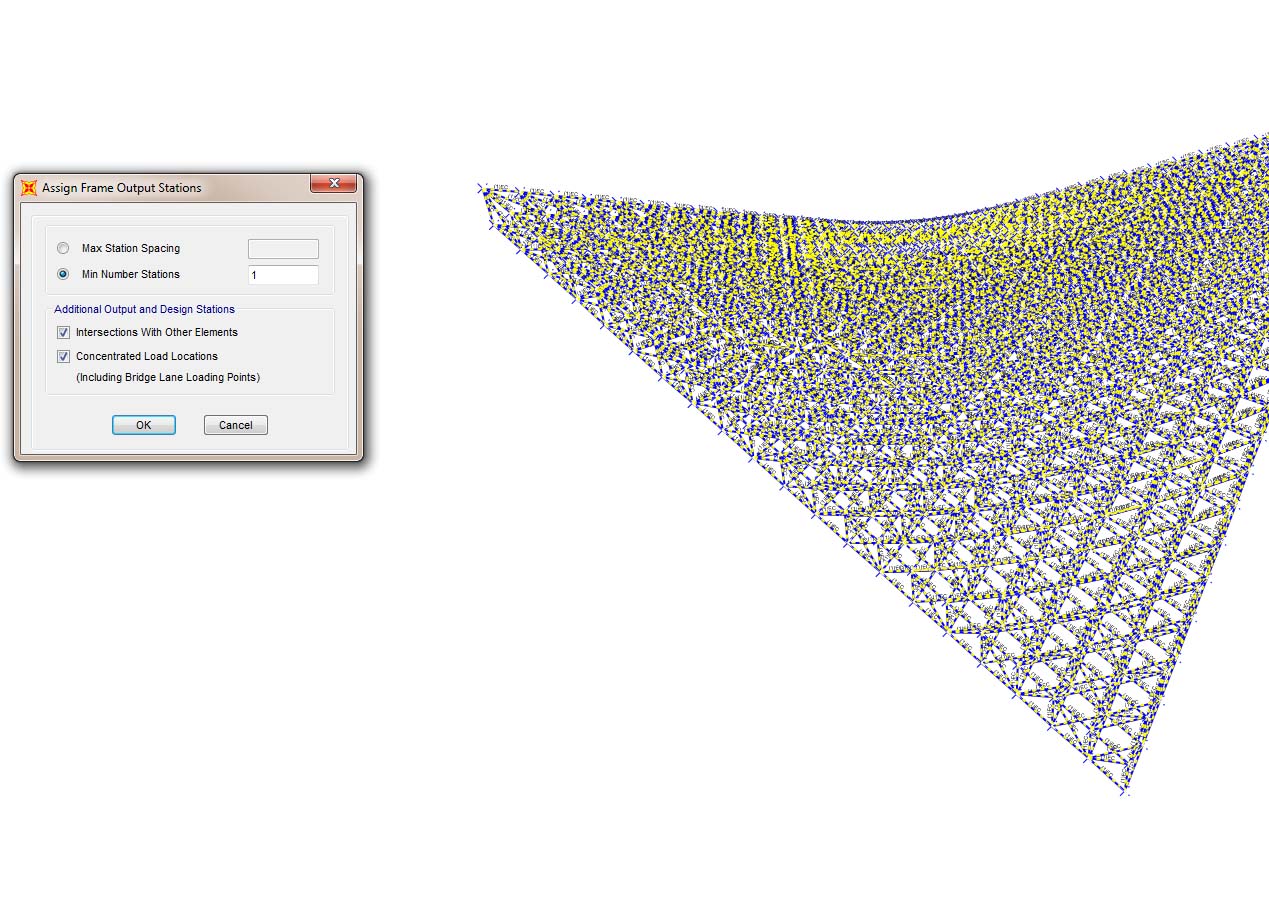
Step-2: impostazione delle cerniere interne con rilascio dei momenti agli estremi dell’asta per tutti i componenti del modello, affinché questo assuma natura di reticolare spaziale;

  

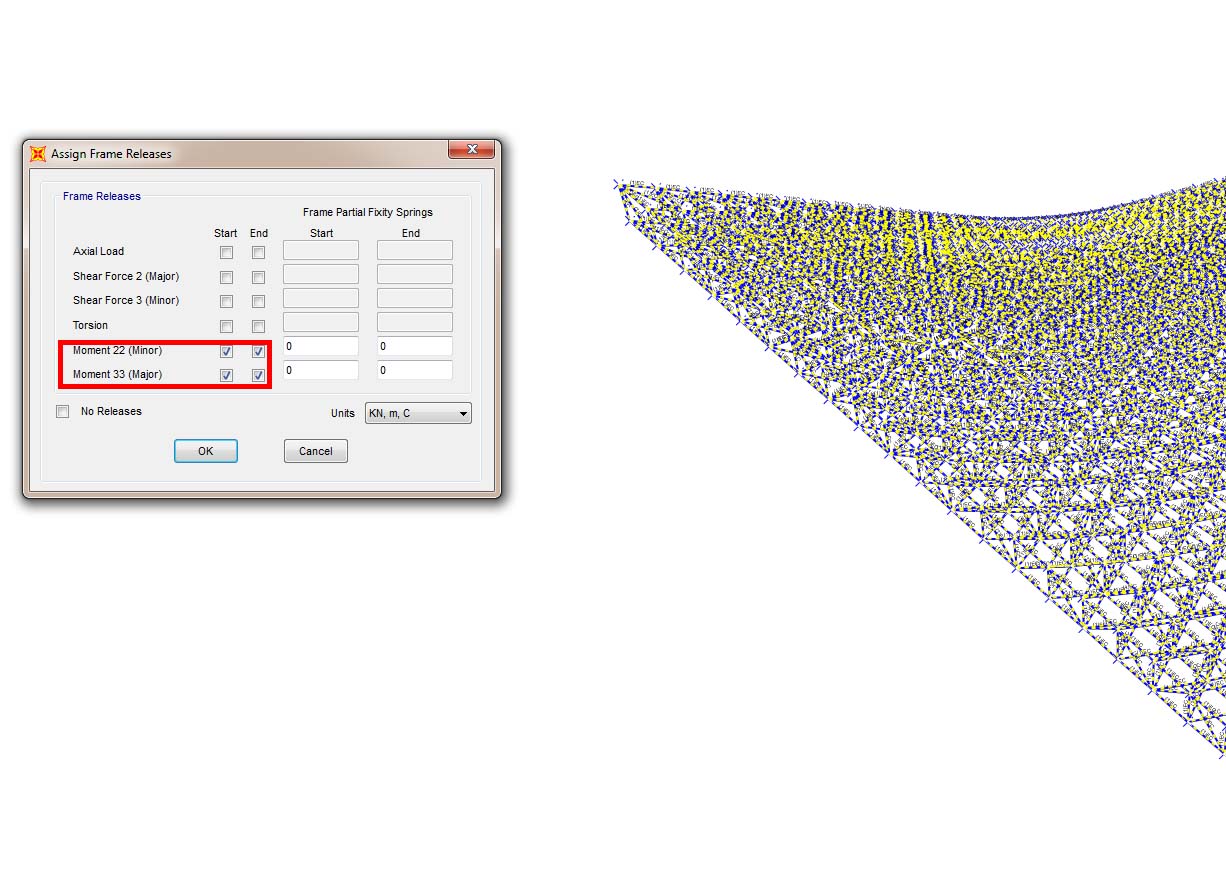
Step-3: definizione e assegnazione di “sezione di progetto” delle aste per il calcolo delle sollecitazioni scelta come tubolare metallico cavo;

 

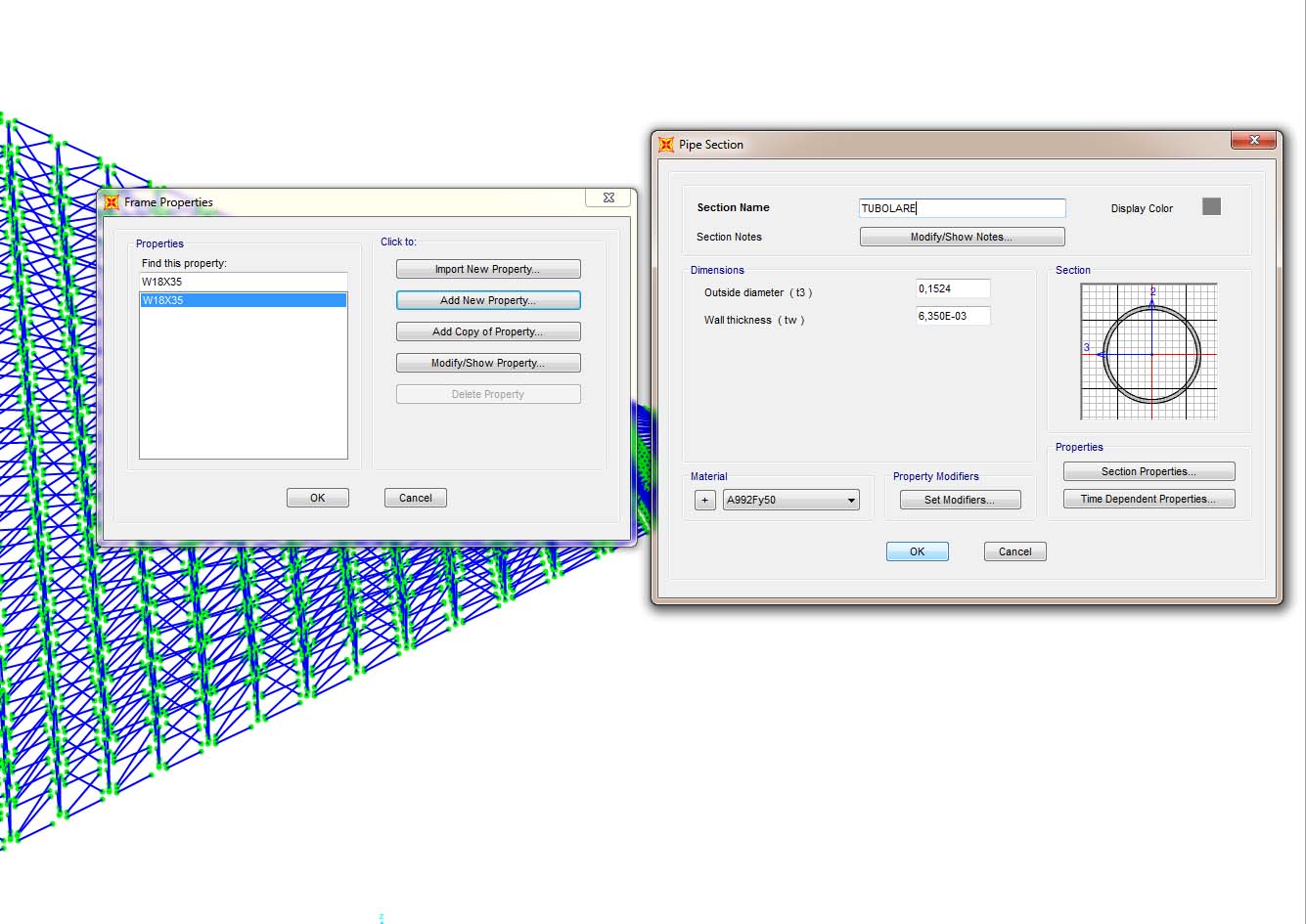
Step-4: assegno di vincoli esterni puntuali su alcuni dei nodi presenti sulla “faccia posteriore” del modello: l’assegnazione di tali cerniere è stato un passaggio complesso dato dal modo di lavorazione del software che sfrutta viste bidimensionali “PER PIANI” che interagiva con un oggetto a curvatura negativa. Per aggirare il problema sono stati assegnati i vincoli esterni andando a selezionare i nodi da una visualizzazione 3d assonometrica del modello, oppure analogamente si poteva lavorare con una visualizzazione bidimensionale in pianta andando a sommare i “piani” che il software evidenziava come sottolinea l’immagine qui di seguito;

  

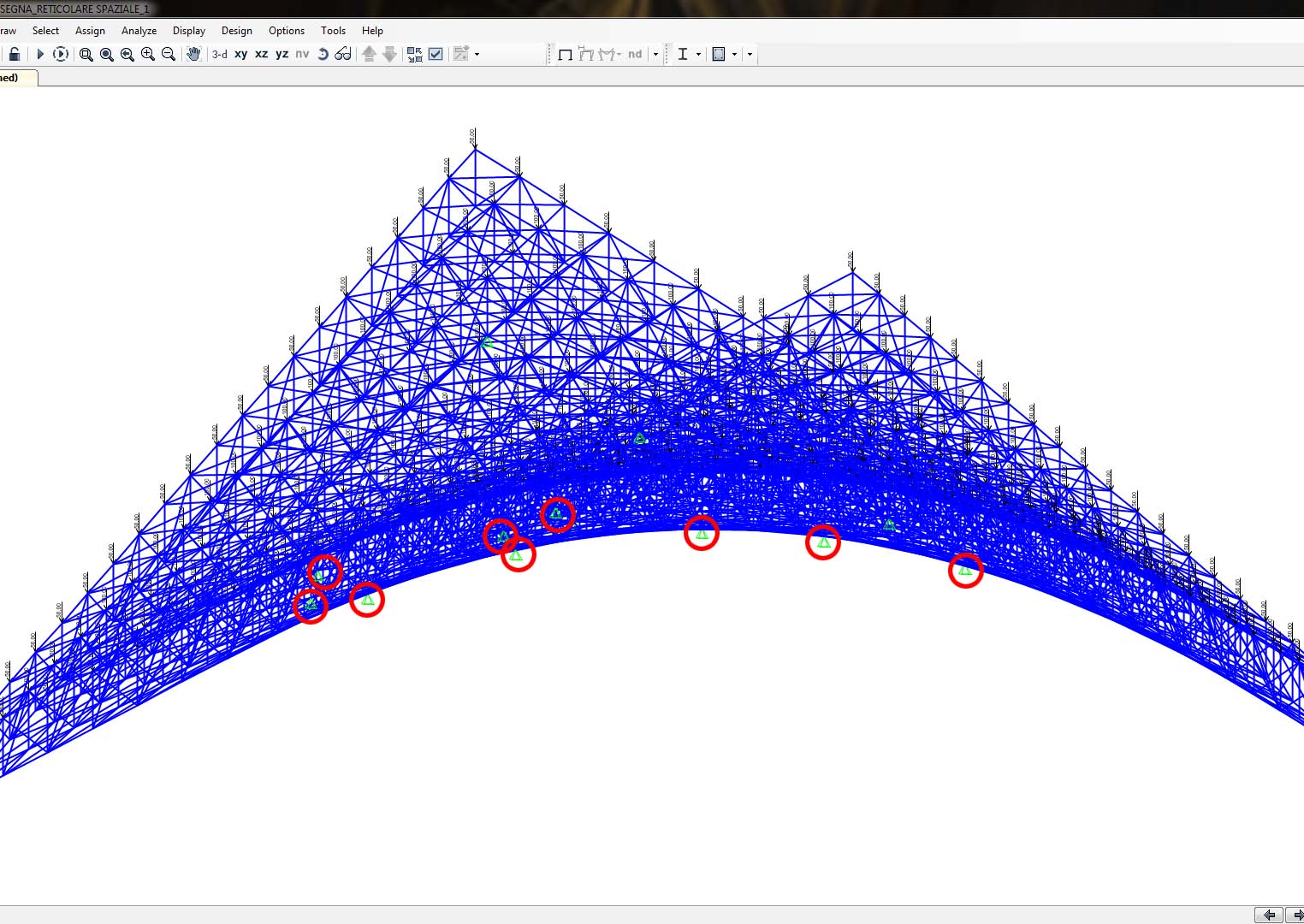
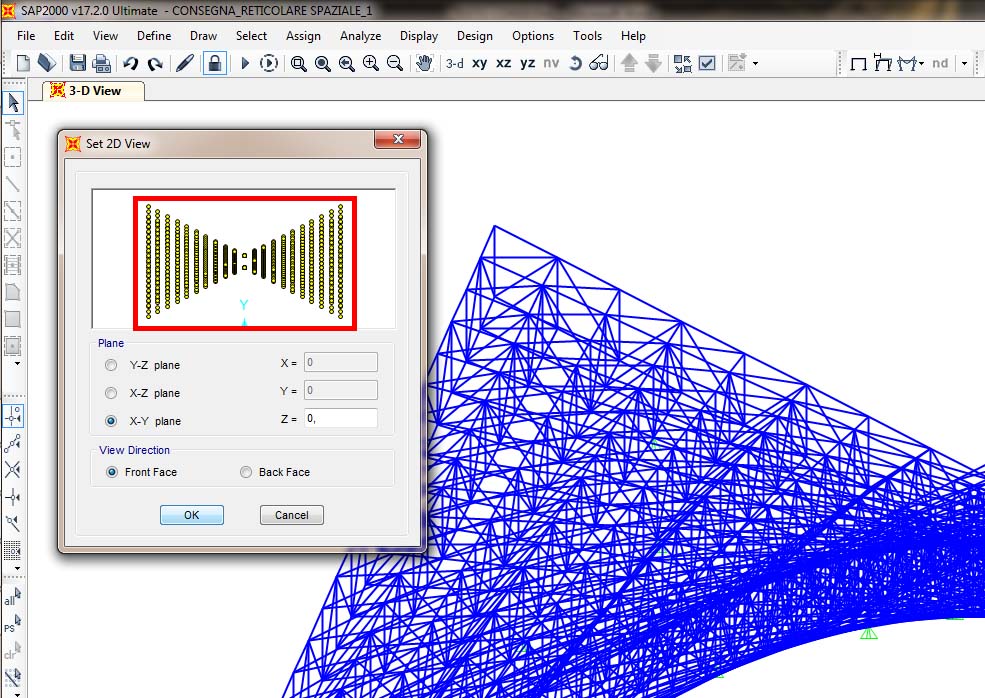
Step-5: definizione di un carico “F” con esclusione del peso proprio della struttura e assegnazione dello stesso come carico uniformemente distribuito ma impostato come carico puntuale, con valore di 100 KN per tutti i nodi presenti sulla faccia superiore del modello.

Essendo un carico distribuito sono stati assegnati carichi puntuali di intensità di 100 KN per tutti i nodi della superficie tranne che per i nodi al perimetro della stessa per cui l’area di influenza del carico distribuito è dimezzata e quindi con intensità di 50 KN;

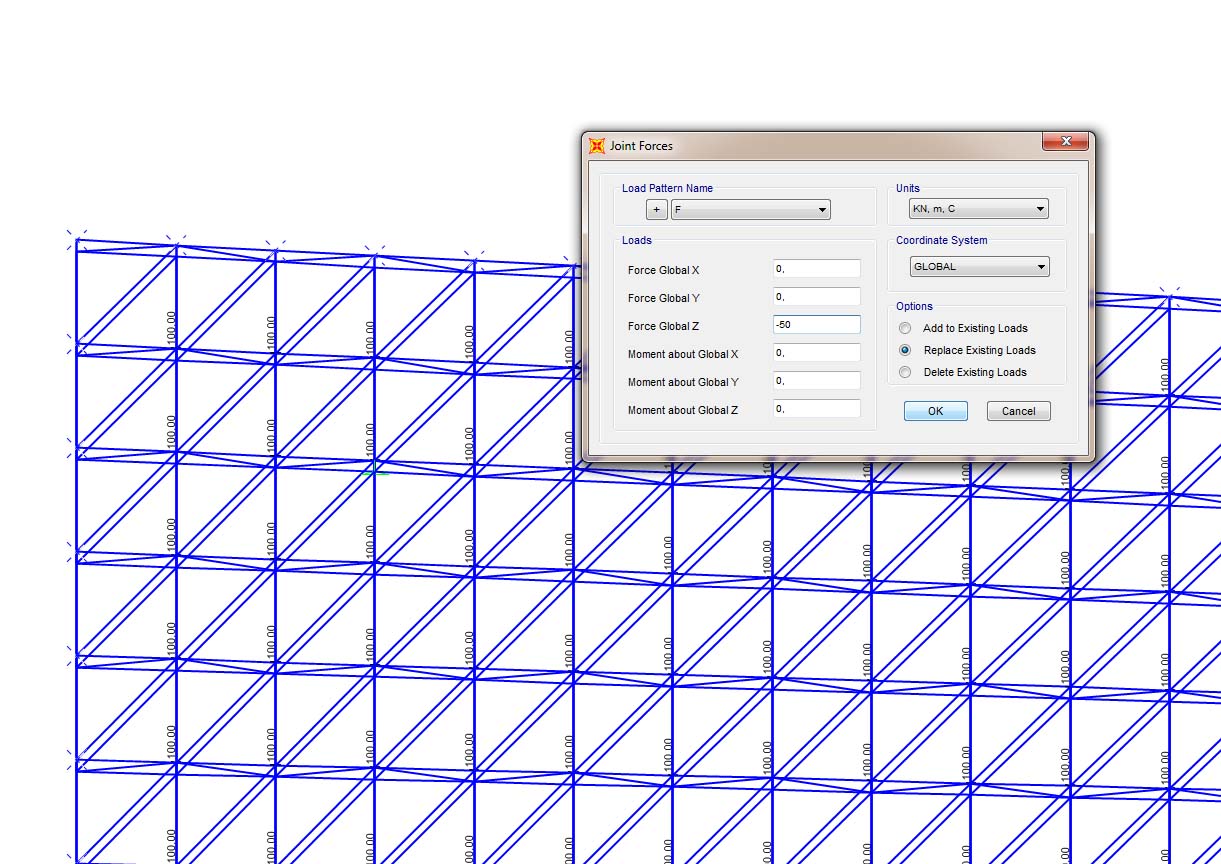
Step-6: calcolo della struttura per il carico impostato “F”;

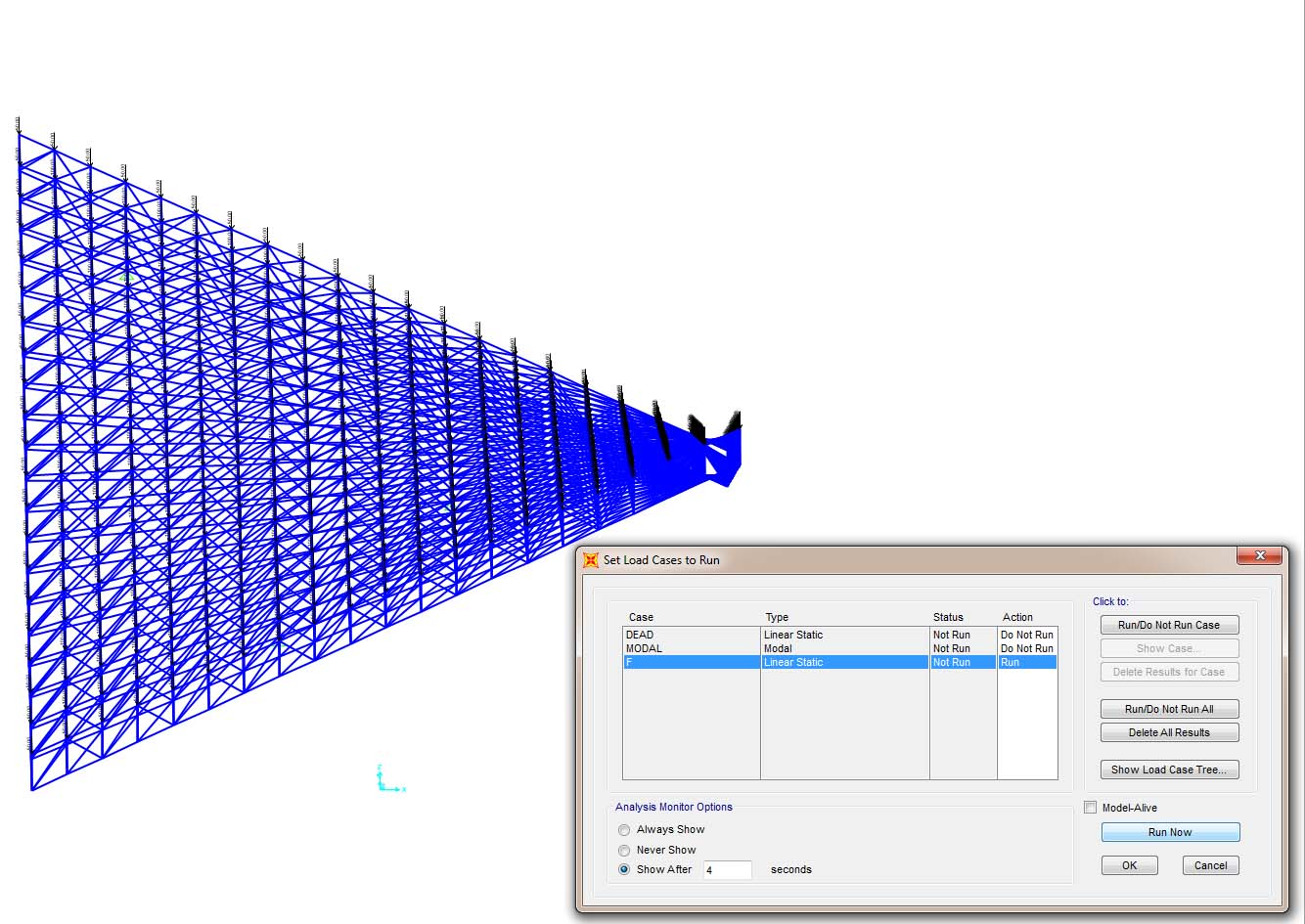
Step-7: visualizzazione della deformata per la sola combinazione di carico “F” definito a posteriori;

  

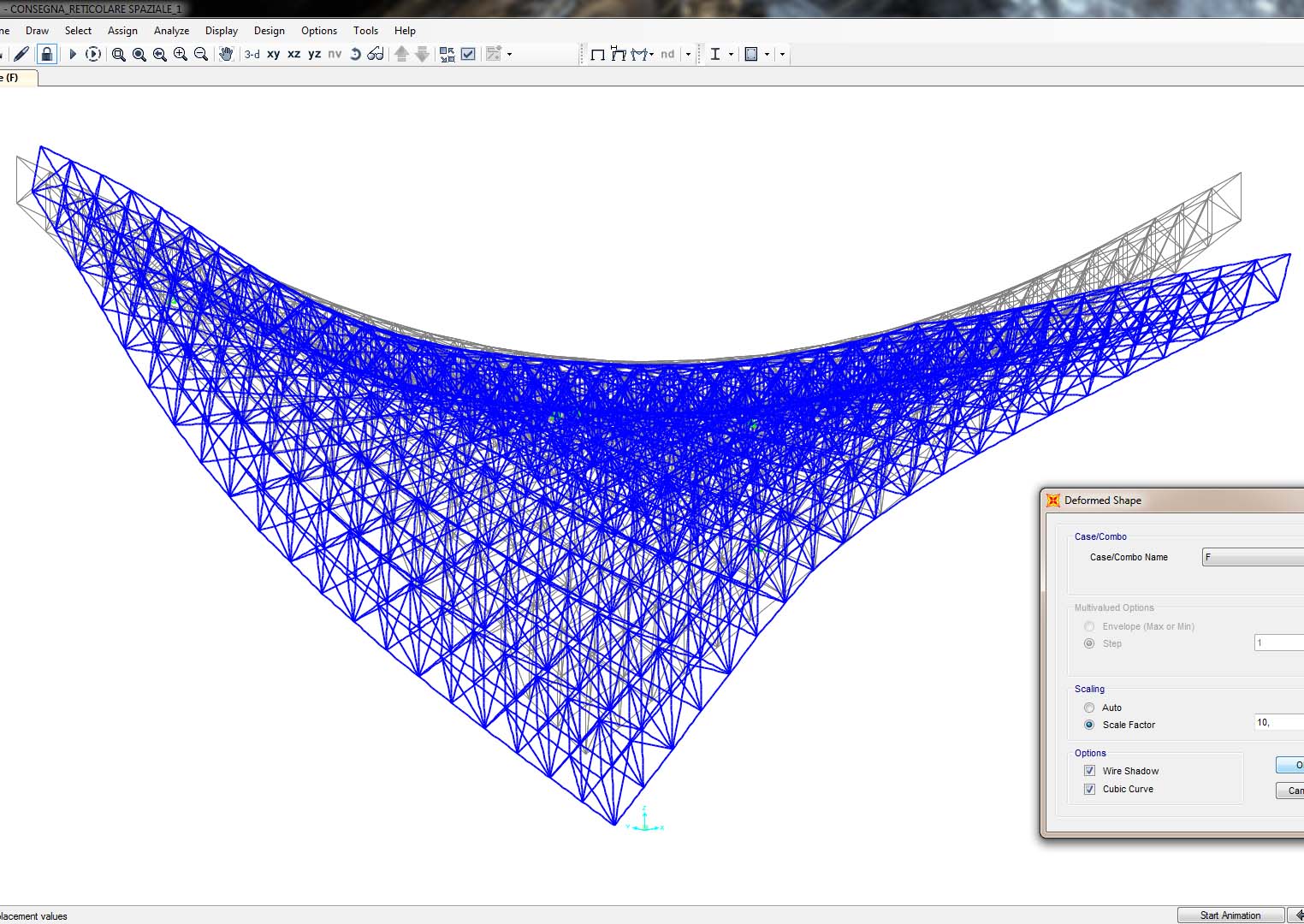
Step-8: analisi dei valori e dei diagrammi degli sforzi normali per tutto il modello (ovviamente di natura costante) – in rosso il software definisce la compressione e in blu la trazione, infatti è possibile notare come i frame collegati direttamente per una estremità al vincolo esterno siano tutti in compressione;

  

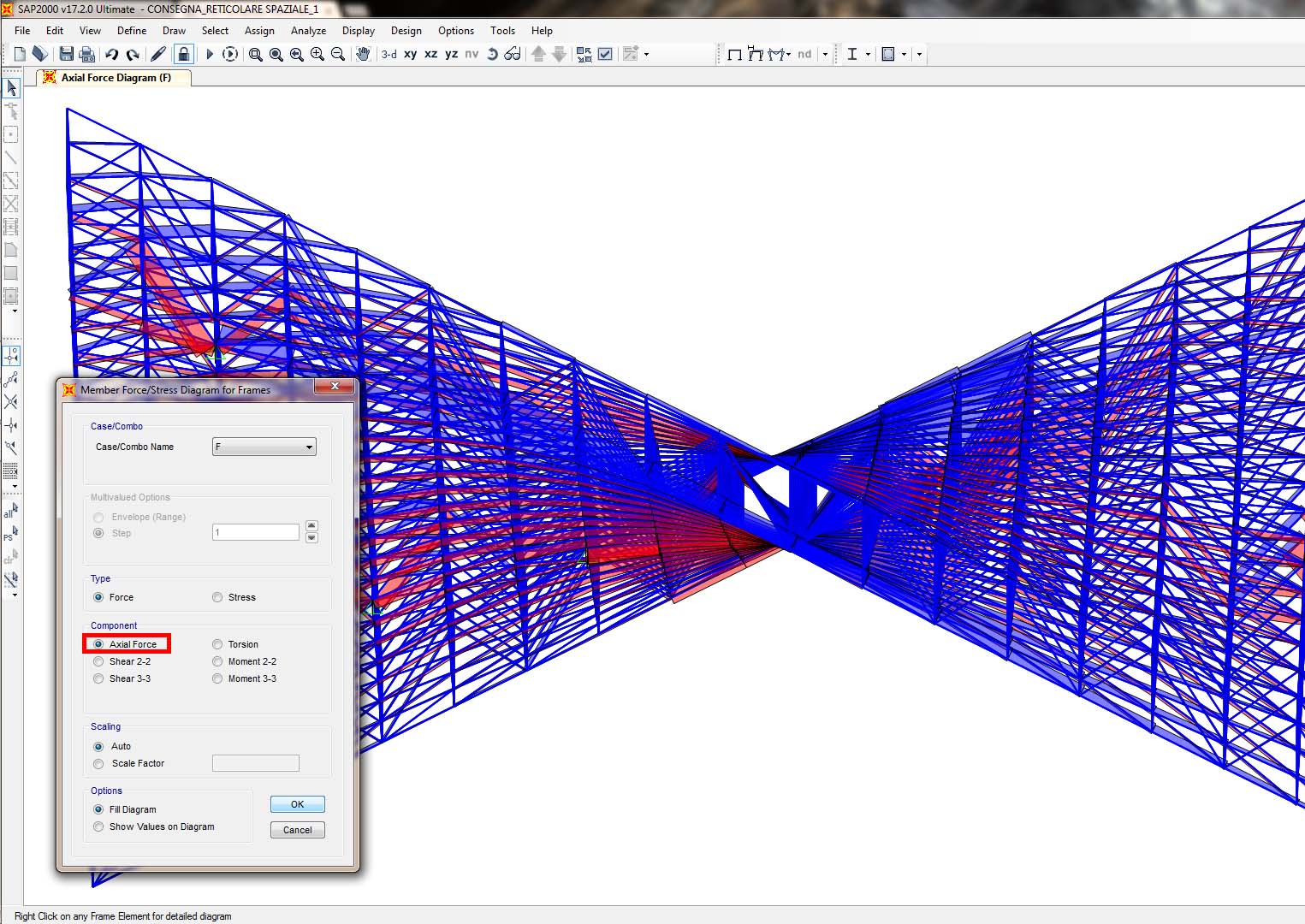
Step-9: esportazione della tabella di analisi delle sollecitazione delle aste da SAP 2000 al foglio elettronico di Excel per il dimensionamento di massima delle aste;

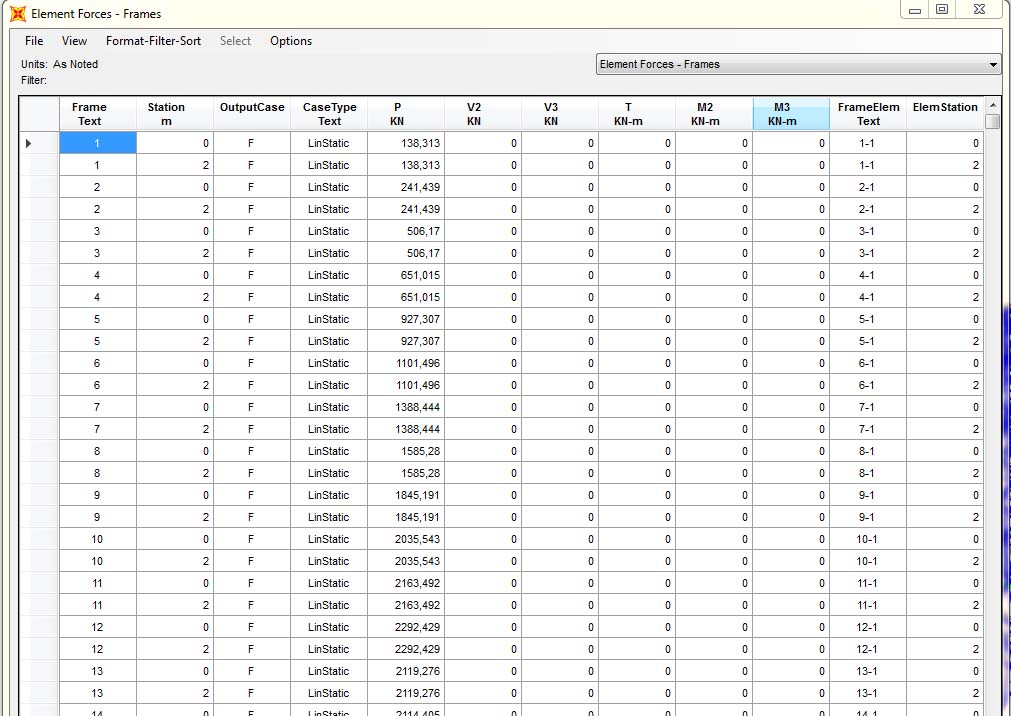
Step-10: per il dimensionamento delle aste del modello di paraboloide iperbolico si ha l’esigenza di differenziare due tabelle che raggruppano i frame compressi e tesi, quindi procedere con i calcoli necessari alla ricerca dell’area minima (Amin) per le aste tese e l’ulteriore calcolo del momento d’inerzia minima (Imin) per le aste compresse soggette anche alla verifica di snellezza della sezione che si va a scegliere da opportuni profilari;

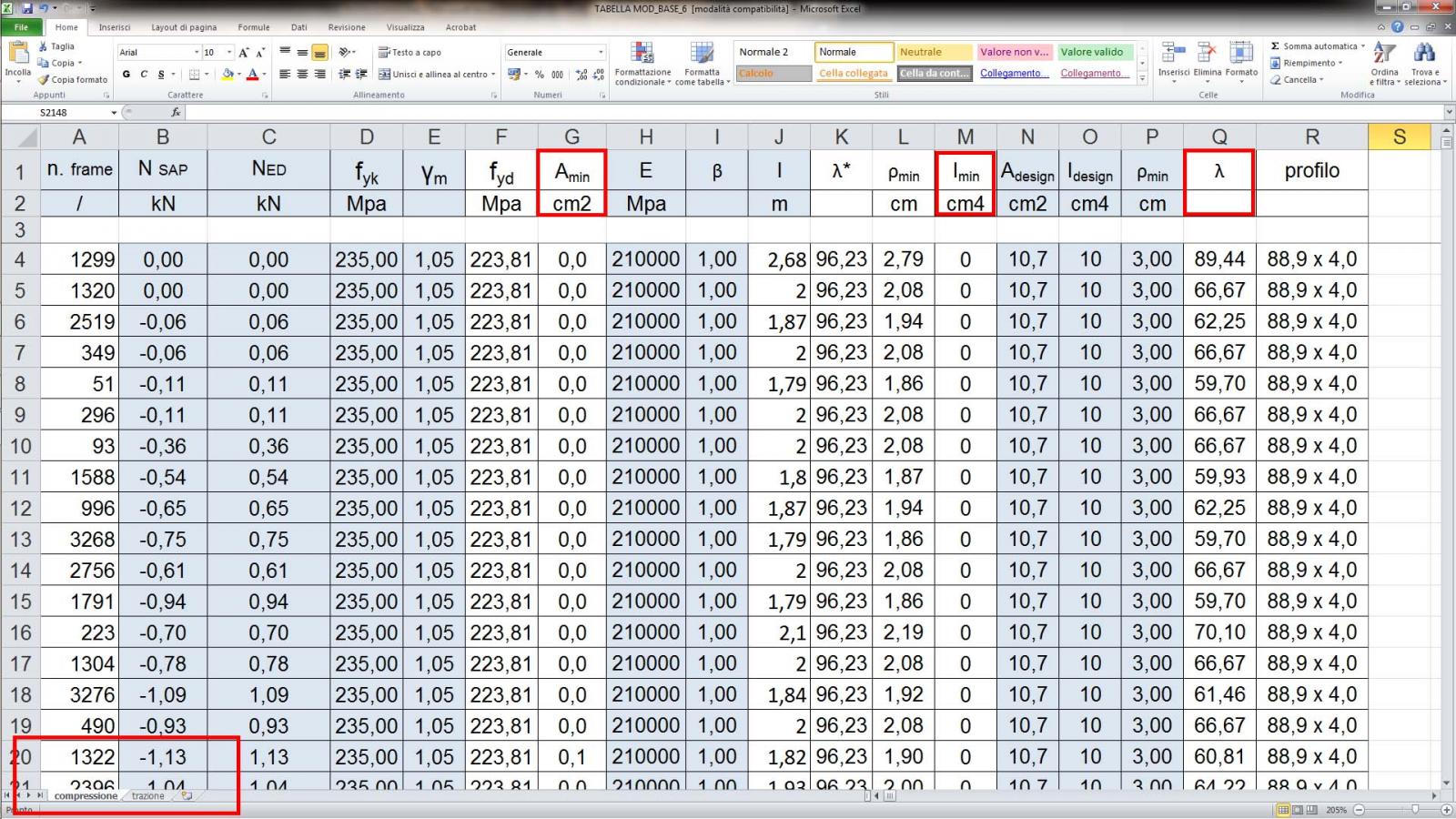
Step-11: dato l’eccessivo numero di frame da calcolare si è scelto di operare attraverso un metodo che riuscisse a semplificare la procedura di dimensionamento eseguendo gli opportuni calcoli descritti sopra dividendo ulteriormente le aste tese e compresse a seconda del valore di sollecitazione a sforzo normale (Ned);

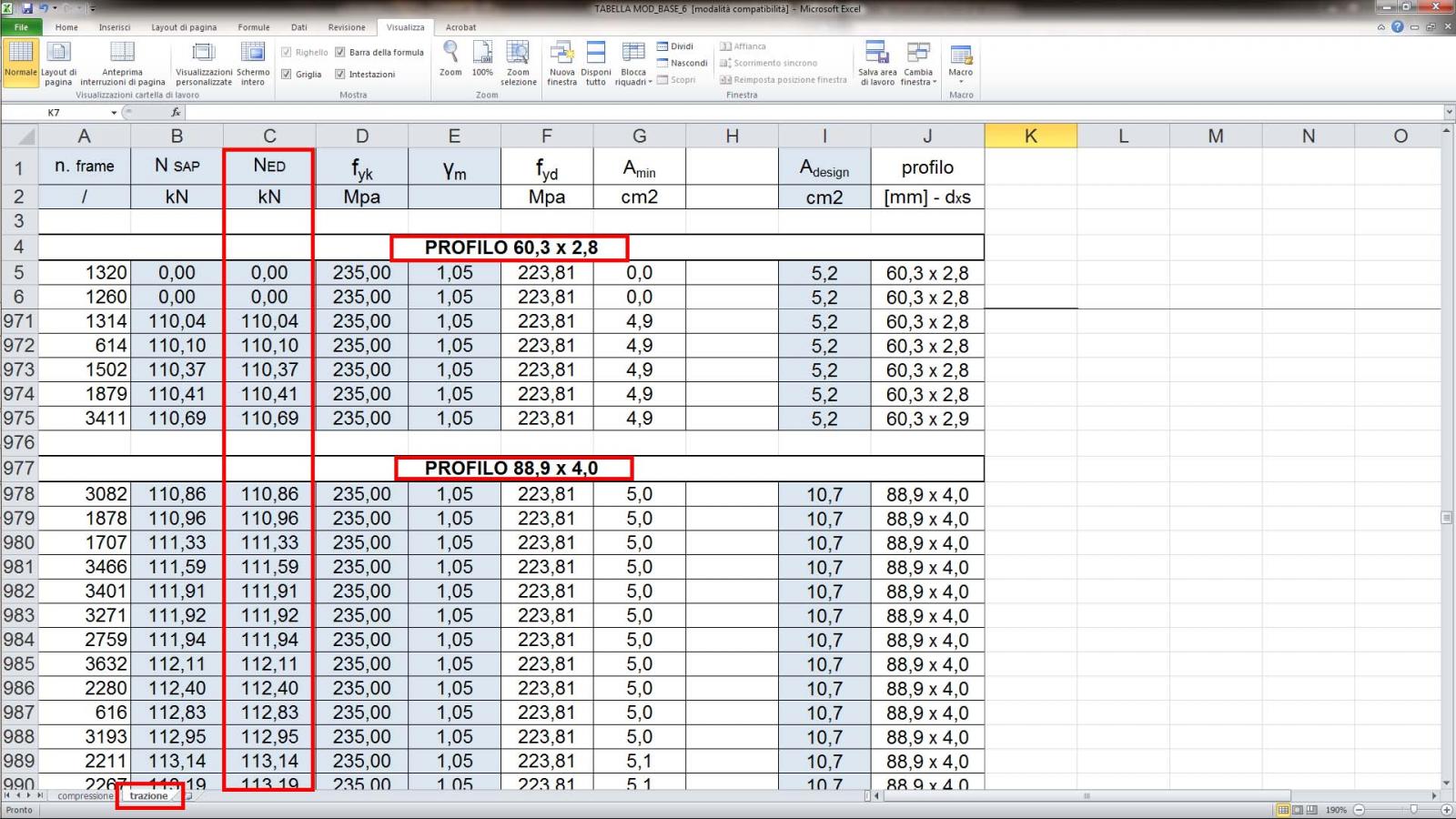
Step-12: per tutte le aste soggette a trazione, dato un valore di sforzo normale di progetto (Ned) – esportato direttamente da SAP 2000, si va a calcolare un’area minima tramite la formula:

 Amin=Ned/Fd

Dove Fd è la resistenza di progetto del materiale scelto, in questo caso acciaio S235, che viene calcolato dalla resistenza del materiale Fyk (235 MPa) diviso il coefficiente di sicurezza γm pari a 1,05 per l’acciaio;

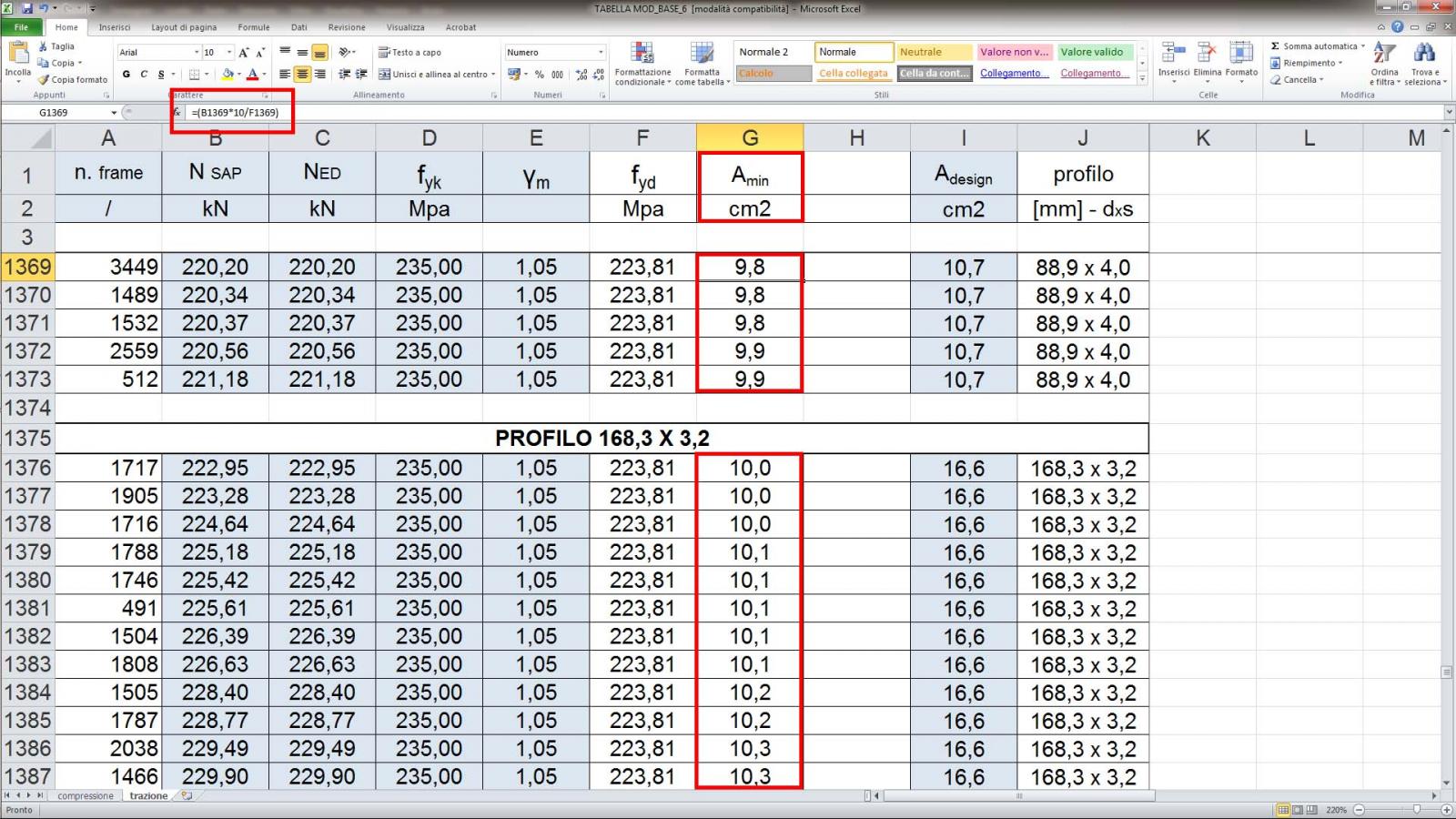
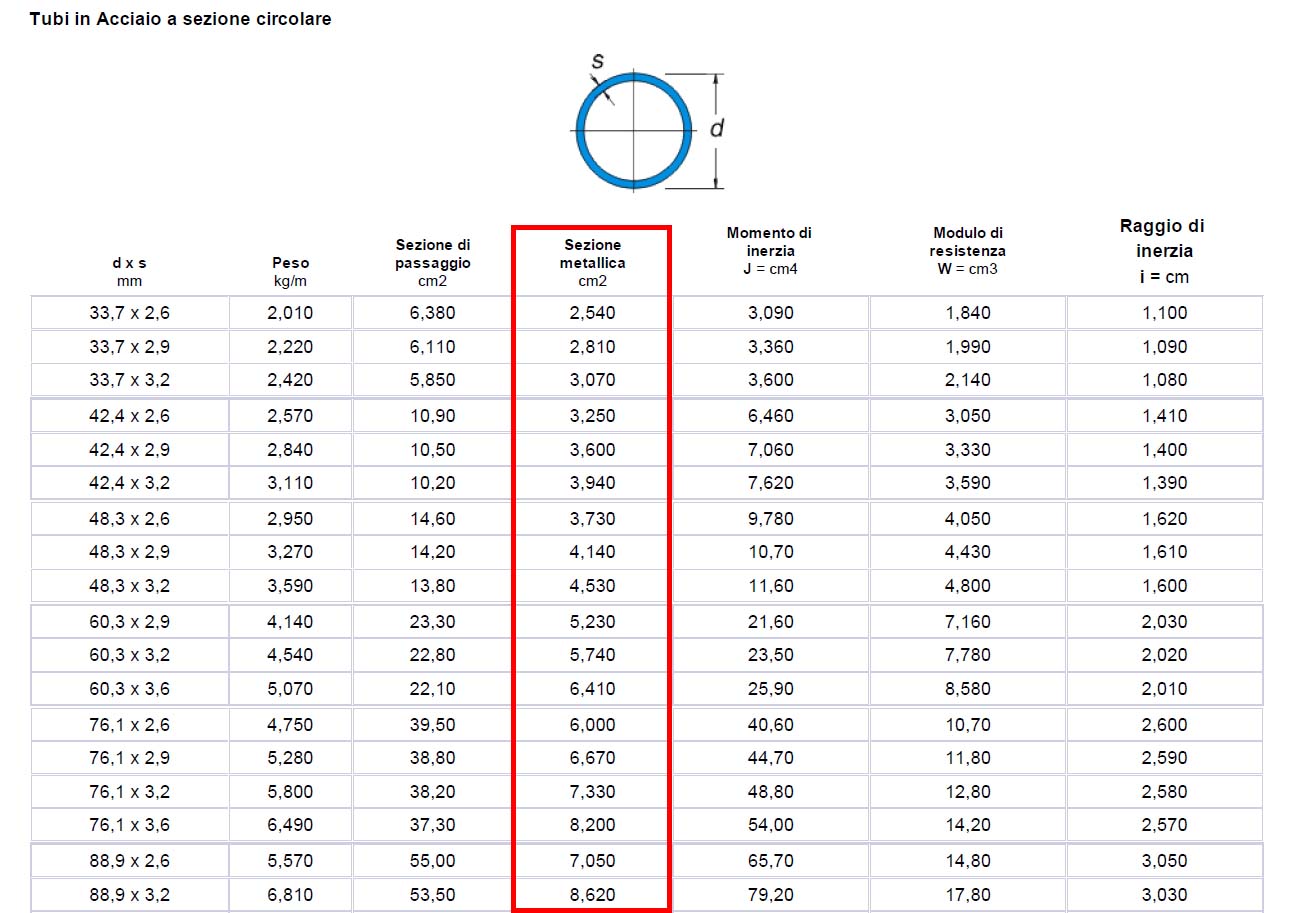
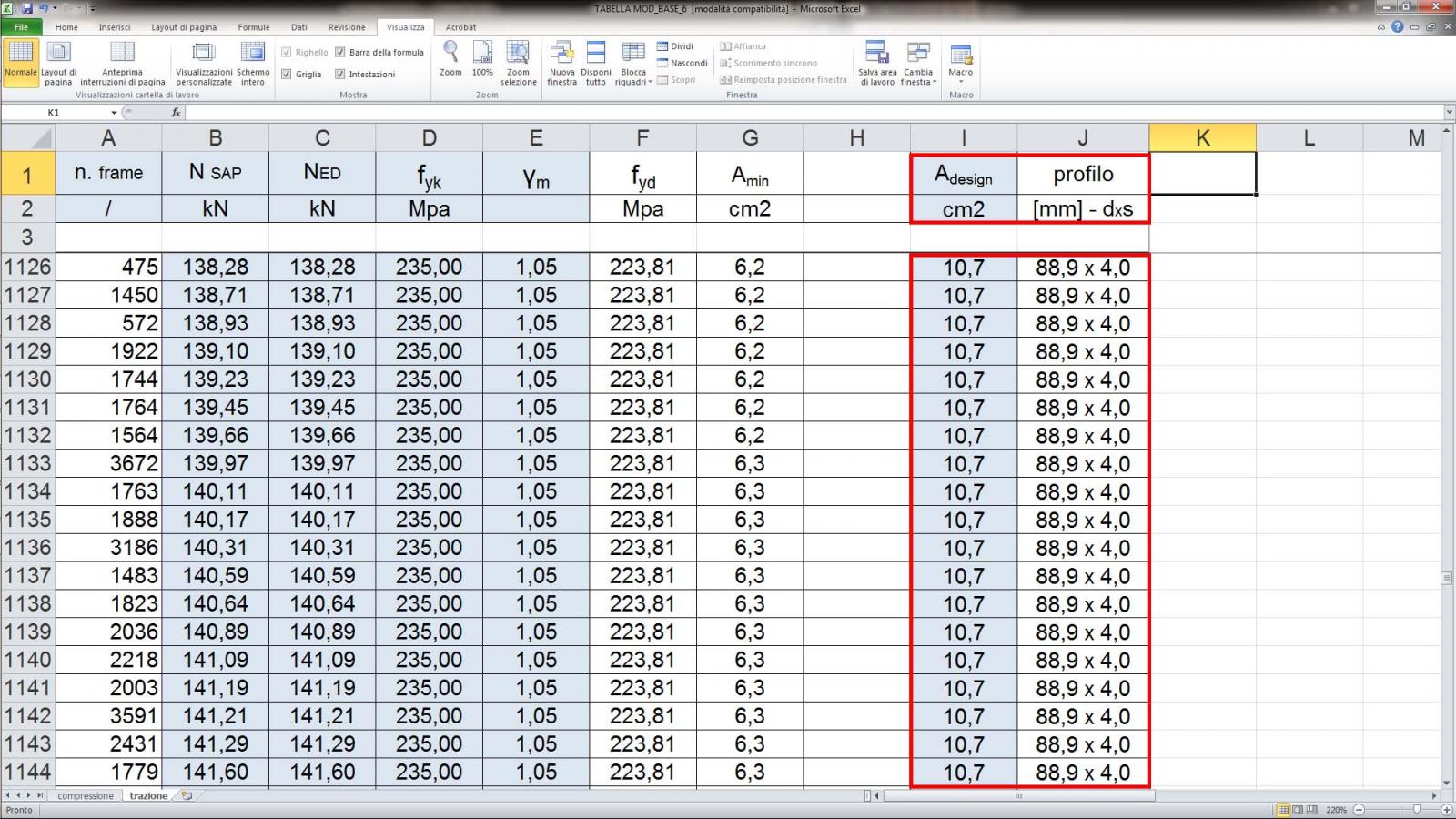
Step-13: ricavata l’area minima di tutte le aste tese, con un opportuno profilario di sezioni tubolari cave in acciaio si va ad assegnare una sezione per ogni categoria di aste, definito dallo step-11, andando a prendere una sezione che abbia un’area (“metallica” nel caso del profilario dell’azienda Oppo) maggiore rispetto all’area minima, definita in tabella con il nome di Adesign e quindi si associa a questa il profilo scelto;

Amin < Adesign

  

Step-14: per il dimensionamento delle aste compresse si segue lo stesso iter processuale delle aste tese con la differenza iniziale del segno dello sforzo normale di progetto da cambiare, con opportuna formula in Excel e il calcolo ulteriore del momento d’inerzia minimo:

Nell’immagine di seguito nella tabella è stata inserita una colonna di Ned che definisce il cambio di segno dell’NSAP esportato direttamente dal software stesso.

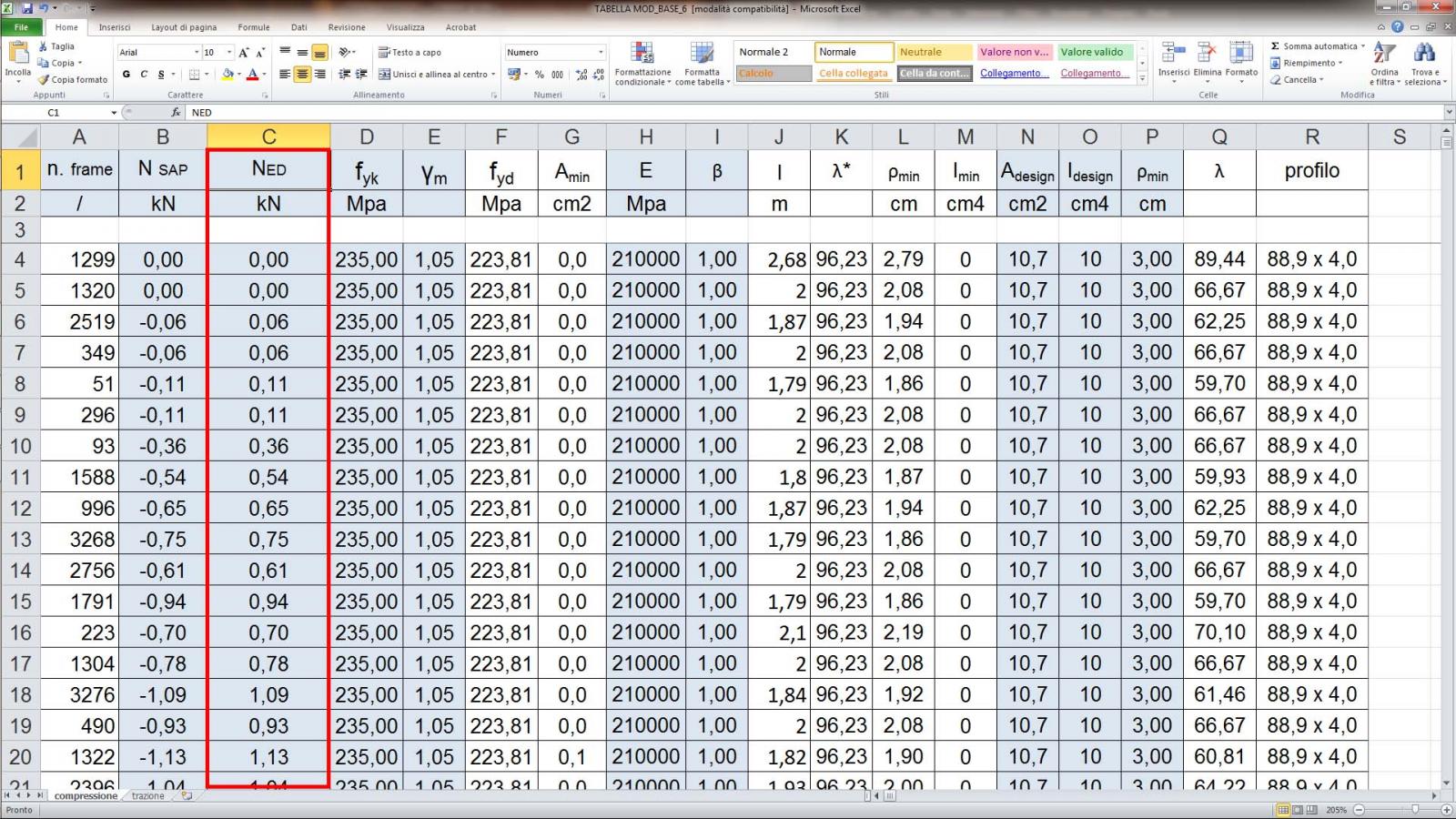
Successivamente, calcolata l’area minima, si procede con il calcolo del momento d’inerzia minimo (Imin) che si ricava dalla formula del carico critico euleriano:

Ncr = π²EA/λ²

Dove E è il modulo di elasticità del materiale, A l’area della sezione e λ è la snellezza della sezione calcolata mediante la formula:

λ=lo/ρmin

dove lo è la lunghezza libera di inflessione che si ricava dal prodotto di β, coefficiente adimensionale che determina le condizioni di vincolo dell’asta (in questo caso essendo ogni asta doppiamente incernierata il coefficiente sarà pari a 1 poiché i flessi saranno localizzati proprio sulle cerniere) e l, lunghezza dell’asta, e che rappresenta la distanza tra due punti di flesso successivi della deformata critica, e ρmin è il raggio d’inerzia ricavabile dalla formula:

ρmin=lo/λmax

quale λmax è la snellezza massima della sezione definibile tramite la formula del carico critico euleriano:

λmax=π RadQ(E/Fd)

dove è tutto noto.

Essendo l’inerzia minima (Imin):

Imin=A ρmin²

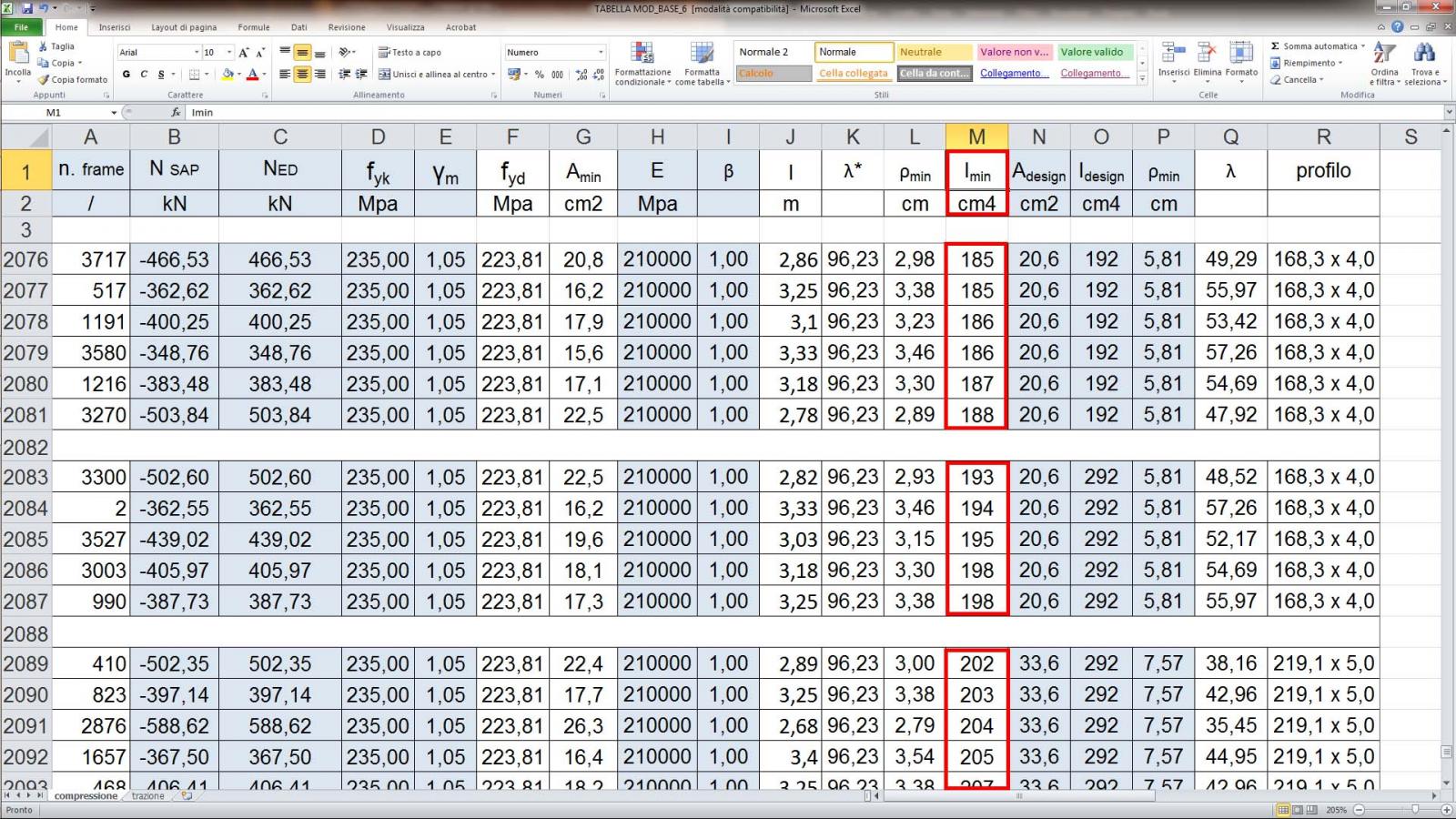
Step-15: una volta ricavati tutti i parametri in Excel delle formule viste prima si avrà sia un’area minima sia un momento d’inerzia minimo e da questi due parametri si potrà scegliere il profilato per ogni asta scegliendo il parametro più restrittivo tra i due;

Step-16: scelto un profilato per ogni categoria di asta compressa, divise come suggeriva lo step-11, si procede ad un ulteriore calcolo normativo di verifica che va ad analizzare la snellezza del profilato scelto:

la normativa impone che la snellezza di un asta non può essere superiore a un valore pari a 200 quindi scelto il profilato adeguato ai due valori di area minima e momento d’inerzia minimo, sempre sul profilario è possibile leggere i valori dei raggi d’inerzia (ρmin) (essendo un tubolare il raggio sarà unico) di tutte le sezioni scelte per calcolare poi la snellezza dell’asta con la formula vista prima:

λ=lo/ρmin

dove:

λ < 200

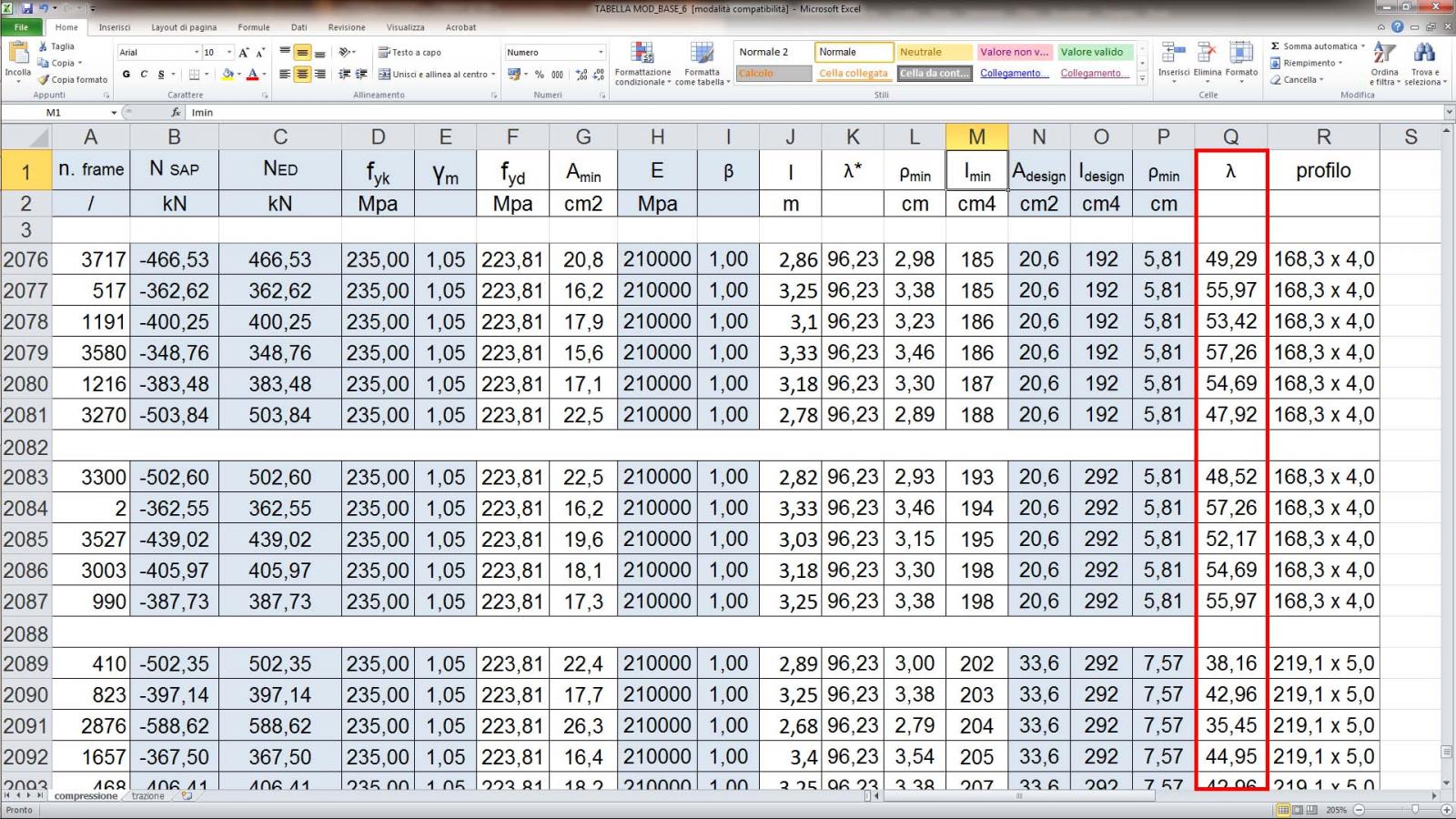
Step-17: dopo questo dimensionamento di massima è possibile effettuare nuovamente le verifiche e le analisi in SAP 2000 andando a definire tutte le sezioni e i materiali scelti, e assegnarli alle apposite aste del modello.

Valerio Minella