SdC(b) (LM PA)

Analisi di una trave iperstatica

Per risolvere una struttura iperstatica il primo passo è associarla ad una struttura isostatica di riferimento, in questo caso posso considerarla come una serie di travi appoggiate con una coppia di forze che bilanciano i momenti nei nodi interni

Ora vado ad analizzare le rotazioni nei nodi B, C, D. Visto che la struttura è simmetrica posso considerare i valori della coppia di momenti in B e in D equivalenti

ϕBs = (ql³ / 24EI) –( x₁l / 3EI)
ϕBd = -(ql³ / 24EI) +( x₁l / 3EI) +(x₂l / 6EI)

ϕBs =-ϕDd      ϕBd =-ϕDs      

Il termine +(x₂l / 6EI) che compare in ϕBd sta ad indicare la rotazione generata dal momento x₂ nel polo opposto a quello analizzato ma che incrementa ulteriormente la deformazione della trave ed assume un valore pari alla metà della rotazione generata dal momento x₂ nel suo polo di applicazione C

ϕCs  =  (ql³ / 24EI) -(x₂l / 3EI) -( x₁l / 6EI)

ϕCd  = - (ql³ / 24EI) +(x₂l / 3EI) +( x₁l / 6EI)

Ora andremo a stabilire l’uguaglianza tra le rotazioni per equilibrare i momenti e metteremo a sistema due coppie di rotazioni per ricavare le incognite

ϕBs =ϕBd     ϕDs =ϕDd     ϕCs  =  ϕCd     (considero ne sistema le coppie B e C)

(ql³ / 24EI) –( x₁l / 3EI)  =  -(ql³ / 24EI) +( x₁l / 3EI) +(x₂l / 6EI)
(ql³ / 24EI) -(x₂l / 3EI) -( x₁l / 6EI)  =   - (ql³ / 24EI) +(x₂l / 3EI) +( x₁l / 6EI)

Dalla prima ricavo x1:    -(2 x₁l / 3EI) = -(ql³ / 12EI) +(x₂l / 6EI)
x₁ = (ql²/8) – (x₂/4)

Ora sostituisco la x₁ trovata nella seconda equazione per trovare l’unica incognita x_2:
(ql³ / 24) = (7x₂l/12)       quindi    x2 = (ql²/14)

Conoscendo il valore di x₂ lo andrò a sostituire nuovamente per ricavare il valore di x₁
(ql³/12) – (ql³/21) = (x₁l/3)       quindi    x1 = (3ql²/28)

Ora sovrapponendo i due schemi potremo ricavare i valori delle forze agenti nei nodi

Conoscendo le forze agenti posso rappresentare il grafico del taglio e del momento

Metodo delle forze

Struttura tre volte iperstatica la studiamo come un corpo isostatico svincolando in B, in C e in D assegnando due momenti incogniti X₁ e X₂ in D sarà sempre X₁ poiche la trave è simmetrica, così da interrompere la trave e creare 4 pezzi di trave isostatica

Per risolvere il sistema parto dai tre momenti e come prima cosa imponiamo la congruenza e scriviamo che le nostre tre equazioni di congruenza siano uguali a zero. 

Nei punti in cui abbiamo inserito le congruenze avremo due equazioni in cui una guarda a destra e una a sinistra. Le eguagliamo e mettendole a sistema andremo a trovare le nostre incognite X₁ e X₂.

Disegno le reazioni vincolari trovate dalla congruenza assegnata e le reazioni date dal carico distribuito

Faccio la sovrapposizione degli effetti sommando i due schemi per trovare le reazioni vincolare della struttura iperstatica. nel primo diagramma ci sono le congruenze.

Nel secondo vediamo le reazioni dovute al carico distribuito

E questa è la sovrapposizione dei due schemi delle reazioni vincolari

Ora possiamo calcolarci i diagrammi delle sollecitazioni di Taglio e del Momento

L’esercitazione presenta una struttura tre volte iperstatica costituita da una trave continua su appoggi. La risoluzione è ottenuta attraverso il METODO DELLE FORZE.

 Si procede nel seguente modo:

1. Si sceglie la struttura isostatica di riferimento  più conveniente ponendo delle  incognite iperstatiche, il cui numero è pari al grado di iperstaticità della struttura. Nel nostro caso, da una trave continua si passa a staccare la struttura in più travi appoggiate-appoggiate. La reazione vincolare incognita che andiamo a scegliere coincide con il momento flettente ed il suo effetto cinematico è quello di evitare la rotazione relativa delle sezioni su cui agisce.

Inoltre ci troviamo di fronte ad una simmetria. Infatti dividendo la struttura a metà (Punto C) notiamo che nella parte destra e nella parte sinistra è presente lo stesso carico distribuito (q) e la stessa luce (l).  Per cui è possibile studiare solamente metà della struttura, perché successivamente avrò le stesse reazioni vincolari e azioni di contatto specchiandola.

Si ricercano quindi solo le incognite x1 (B) e x2 (C) . 

2. Si scrivono le equazioni di compatibilità cinematica che ripristinano i vincoli cinematici soppressi dalla trasformazione del vincolo cinematico in reazione vincolari. In questo caso impongo che le rotazioni a destra e a sinistra rispettivamente dei punti B e C siano uguali in quanto la rotazione relativa deve essere nulla.

3. Si risolve il sistema di equazioni per la determinazione delle incognite iperstatiche x1 e x2.

4. Indico le reazioni vincolari e si procede con l’applicazione del principio di sovrapposizione degli effetti per la determinazione delle azioni di contatto sulla struttura iperstatica.

5. I conseguenti diagrammi del taglio e del momento.

Nel metodo delle forze, le incognite sono le reazioni vincolari iperstatiche e le equazioni risolutive sono equazioni algebriche, che hanno il significato meccanico di equazioni di vincolo. La difficoltà sta nel riuscire a scegliere bene la struttura isostatica equivalente e nella capacità di applicazione sistematica del principio di sovrapposizione degli effetti.

Esercitazione trave iperstatica_metodo delle forze

Il Metodo delle Forze, che ha una profonda parentela con il Principio dei Lavori Virtuali, è uno dei possibili metodi per la risoluzione di strutture iperstatiche e consiste primariamente nel porre come incognite del problema alcune reazioni vincolari, il cui numero è pari al grado di iperstaticità della struttura in esame.

Definite queste incognite in modo opportuno, ossia senza “labilizzare” la struttura di partenza, il metodo procede, tramite una sistematica applicazione del principio di sovrapposizione degli effetti, nella determinazione delle equazioni che ci consentono di determinare il valore delle suddette incognite. Queste equazioni sono di compatibilità cinematica: difatti, la scelta di rappresentare qualche grado di vincolo tramite la reazione (forza o coppia) corrispondente, elevandola al rango di incognita, equivale all'eliminazione di alcuni vincoli cinematici, che devono essere ripristinati in termini di equazioni, affinché il sistema isostatico che si sta studiando corrisponda al sistema iperstatico di partenza.

Prendiamo quindi una struttura iperstatica, nel nostro caso 3 volte, ed applichiamo il Metodo delle Forze per determinare gli sforzi di Momento, Taglio e Normale.

Divido la struttura in una successione di travi appoggiate:

L'orientamento delle coppie è dato per equilibrare l'azione dei MOMENTI introdotti in precedenza. Sommo facendo un passo alla volta:

Avendo un carico distribuito so già che il diagramma del MOMENTO sarà descritto da una funzione parabolica e, conseguentemente, quello del TAGLIO da una lineare. Posso anche già dire che in presenza delle forze puntuali il diagramma del TAGLIO avrà una discontinuità (SALTO), e che dove il taglio si annulla il MOMENTO avrà la tangente orizzontale (MASSIMO o MINIMO).

Posso quindi fare un primo disegno QUALITATIVO del momento mentre del taglio so già i valori (REAZIONI VINCOLARI):

Per torvare i valori dei momenti faccio i tagli e sfrutto la simmetria:

Esercitazione 4

Metodo delle forze

Soluzione di una struttura tre volte iperstatica

N.B.

Sono noti i valori della rotazione per la trave appoggiata a cui sono applicati:

a.       un carico uniformemente distribuito

φ₁  = ql²/24EJ

b.      un momento applicato ad un estremo

φ₁  = xl/3EJ

φ₂= xl/6EJ

Analizzando qualitativamente I vincoli, si possono fare alcune considerazioni utili ai fini della risoluzione del sistema:

Nel punto B la rotazione delle sezioni dev’essere uguale da sinistra e da destra.

Lo stesso avviene per il punto C e il punto D.

Φ_{b sx}=  Φ_{b dx}

Φ_{c sx}=  Φ_{c dx}

Metodo delle forze

Posso concepire un sistema isostatico equivalente, dal punto di vista cinematico, a quello dato, per procedure con la risoluzione del sistema.

Tale sistema sostituisce all’unica trave una serie di travi appoggiate di luce l e collegate da carrelli, sui quali viene applicato un momento di valore incognito x, che deve servire a compensare il rilascio alla rotazione relativa effettuato attraverso il distacco dei tratti di trave.

N.B.

Analizzando la struttura dal punto di vista qualitativo, ci si accorge che questa ha caratteri di simmetria che consentono di ipotizzare che le reazioni vincolari siano in B e D uguali (e quindi anche i momenti applicati in quei punti del sistema equivalente), come pure in A ed E.

Riepilogando:

R_a = R_e ;

R_b = R_d ;

x₁ = x₃

(B)

Φ_{b sx}=  -(x₁l / 3EJ) + (ql³ / 24EJ)

Φ_{b dx}= (x₁l / 3EJ) – (ql³ / 24EJ) + (x₂l / 6EJ)

(C)

Φ_{c sx}=  -(x₂l / 3EJ) - ( x₁l / 6EJ) + (ql³ / 24EJ)

Φ_{c dx}= (x₂l / 3EJ) - (ql³/ 24EJ) + (x₃l / 6EJ)

Eguaglio a due a due queste equazioni (sostituendo anche x₃ con x₁), andando ad impostare un sistema di due equazioni in due incognite (x₁ e x₂).

ì-(x₁l / 3EJ) + (ql³/ 24EJ) = (x₁l / 3EJ) – (ql³/ 24EJ) + (x₂l / 6EJ)

í

î-(x₂l / 3EJ) - ( x₁l / 6EJ) + (ql³ / 24EJ) = (x₂l/3 EJ) - (ql³ / 24EJ) + (x₃l / 6EJ)

ì-2x₁l /3 = (-ql² / 4) (-3 / 2l)  => x₁ = (ql² / 8) – (x₂ / 4)

í

î(- x₂l / 3) – (l/6) [(ql²/8) – (x₂ / 4)]+ ql³ / 24 = (x₂l / 3) – (ql³ / 24) + (l/6) [(ql²/8) – (x₂ / 4)]

ì------------------

í

î- (2x₂l / 3) – (l/3) [(ql²/8) – (x₂ / 4)]+ ql³ / 12 = 0

ì------------------

í

î- (2x₂l / 3) – (ql³ / 24) + (ql³ / 12) (x₂ / 12) = 0

per cui

x₂ = ql² / 4=> x₁ = 3ql² / 28

Ora si procede grazie al principio di sovrapposizione degli effetti: infatti il sistema equivalente può essere inteso come sovrapposizione di due sistemi in cui, come forze esterne, una volta viene considerato solo il carico distribuito (schema q) ed una volta solo i momenti applicati sui carrelli, il cui valore è stato appena definito (schema x).

Si trovano le reazioni vincolari dei due sistemi per poi sommarle (sovrapposizione degli effetti):

Schema x:

R_{a x} = x₁/l

R_{b x} = (x₁/l) + (x₁ – x₂)/l

R_{c x} = 2 [(x₁ – x₂)/l]

Schema q:

R_{a q} = R_{e q} = ql/2

R_{b q}= R_{c q} = R_{d q} = ql

N.B.

Le reazioni sono calcolate analizzando separatamente ogni asta appoggiata-appoggiata e poi sommando I risultati ottenuti sui punti in comune delle aste adiacenti.

Schema equivalente completo:

(ipotizzando la reazione risultante verso l’alto)

R_a = ql/2 – (3ql²)/l = 11ql/28

R_b = ql – [(3ql²/14) – (ql²/14)]= ql + (2ql/14) = 8ql/7

R_c = -(2/l) [(3ql²/28) – (ql²/14) + ql = ql – (2ql/28) = 13ql/14

Ora si procede con l’analisi delle sollecitazioni di taglio e momento:

L'esercitazione ci chiede di fare un progetto di massima della trave maggiormente sollecitata in un solaio, com l'aiuto di un foglio di calcolo che in base a determinati parametri che stabiliamo ci fornisce l'altezza che dovrà avere.
L'esercizio è stato svolto per tre tipologie costruttive diverse: solaio in legno, solaio in acciaio e solaio in latero-cemento

TRAVE IN LEGNO LAMELLARE

Per poter progettare una trave dobbiamo stabilire alcune cose, tra cui i materiali con i loro pesi specifici, e i carichi a cui è soggetta la trave che si dividono in:

-carichi strutturali (qs) cioè tutti i carichi esercitati dalla struttura del solaio, quali travi, travetti e caldana

-carichi permanenti (qp) cioè il peso dei materiali di finitura, dei tramezzi, degli impianti, e di altri elementi gravanti in maniera permanente su du essa

-carichi accidentali (qa) sono dettati dalla normativa in base alla destinazione d'uso

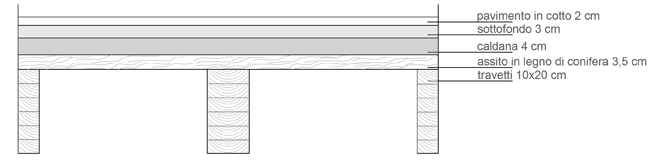
Il solaio in legno sarà composto da:

1. travetti in legno lamellare di conifera 10x20 con peso specifico di 5,3 KN/m3
2. assito in legno di conifera con p.s. di 4 KN/m3
3. caldana di malta cementizia con p.s. 25 KN/m3
4. sottofondo composto da malta di calce con p.s. 18 KN/m3
5. pavimento in cotto con p.s. 18 Kn/m3

La porzione di solaio presa in considerazione per svolgere i calcoli sarà di un metro quadrato, quindi dobbiamo andare a verificare quanto pesa ogni strato in base allo spessore che abbiamo scelto.

CARICHI STRUTTURALI

-travetti in legno (10x20 cm)= (0,1m*0,2m*1m)*5,3 KN/m3 = 0,106 kN/m      i travetti hanno un interasse di 0,50 m, se dividiamo il  risultato pe rinterasse ci viene   fornito il peso di tutti i travetti compresi in quell'aria di studio (in questo caso 2) 0,106/0,5 = 0.212 KN/mq

-assito in legno (s=3,5 cm) = (0,035m*1m*1m)*4 KN/m3 = 0,14 kN/mq

-caldana (s=4 cm) = (0,04m*1m*1m)*25 KN/m3 = 1 kN/mq

qs= 1 + 0,14 + 0,212 = 1,352 KN/mq

CARICHI PERMANENTI

-sottofondo (s=3 cm)= (0,03m*1m*1m)*18 KN/m3 = 0,54 kN/mq

-impianti = vengono calcolati circa 0,5 KN/mq

-tramezzi = vengono calcolati circa 1 KN/mq

-pavimento (s=2 cm) = (0,02m*1m*1m)*18 KN/m3 = 0,36 KN/mq

qp= 0,54 + 0,5 + 1 + 0,36 = 2,40 kN/mq

CARICHI ACCIDENTALI

- per civile abitazione 2 kN/mq

Inseriamo i dati richiesti nel folgio di calcolo: INTERASSE= aria di influenza della trave (4m), i carichi appena calcolati, la luce della trave (6m), e la base della trave scelta da noi (30cm)

Il foglio ci restituisce una trave alta 45,66 cm, e per approssimazione scegliamo una sezione di 30x50 cm

La trave deve sostenere anche il proprio peso, quindi dobbiamo procedere con la verifica aggiungendo al carico strutturale il peso di quest'ultima, che al metro lineare sarà (0,3m*0,5m*1m)*6 KN/m3 = 0,90 kN/m

Dobbiamo fare un piccolo passaggio in più dato che nel foglio di calcolo il qs viene moltiplicato per l'interasse (area di influenza) mentre il peso della trave principale non agisce su tutta quest'area, ma solo su se stessa. Quindi dividiamo il risultato per l'area di influenza (4m).

-trave in legno (30x50cm) = 0,90 KN/m / 4 m = 0,225 kN/mq

qs = 1,352 kN/mq + 0,225 kN/mq = 1,577 kN/mq

L'altezza è aumentata a 46,55 cm, nettamente inferiore alla nostra sezione scelta, quindi la trave è VERIFICATA

TRAVE IN ACCIAIO

Scegliamo una lamiera grecata in base al carico complessivo al metro quadrato calcolato per il solaio precedente (qs+qp+qa = 5,752 KN/mq)

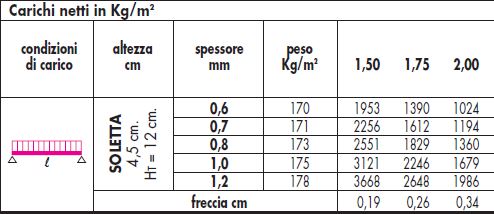
Scegliamo una lamiera con soletta di 4,5 cm, altezza della grecata 12 cm e spessore 0,6 mm. Il peso 170kg/mq = 1,7 KN/mq con un interasse di 2 m. Il carico netto  che può sopportare è 1024 kg/mq = 10.24 KN/mq (nettamente superiore al nostro)

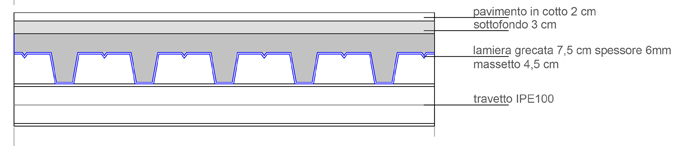
Il solaio sarà composto da:

1. travetti IPE 100 con peso specifico 0.081 KN/m
2. lamiera grecata con massetto con p.s. di 1,7 KN/mq
3. sottofondo composto da malta di calce con p.s. 18 KN/m3
4. pavimento in cotto con p.s. 18 KN/m3

CARICHI STRUTTURALI

-travetti IPE 100 = 0,081 KN/m / 2m (diviso interasse tra i travetti) = 0,0405 KN/mq

-lamiera+massetto = 1,7 KN/mq

qs= 0,0405+1,7 = 1,7405 KN/mq

CARICHI PERMANENTI

-sottofondo (s=3 cm)= (0,03m*1m*1m)*18 KN/m3 = 0,54 kN/mq

-impianti = vengono calcolati circa 0,5 KN/mq

-tramezzi = vengono calcolati circa 1 KN/mq

-pavimento (s=2 cm) = (0,02m*1m*1m)*18 KN/m3 = 0,36 KN/mq

qp= 0,54 + 0,5 + 1 + 0,36 = 2,40 kN/mq

CARICHI ACCIDENTALI

- per civile abitazione 2 kN/mq

Inseriamo i dati nel foglio di calcolo, scegliamo la classe di resistenza Fe 430/s275 (sigma dello snervamento=275)

La sigma ammissibile sarà 275/1.15 (coefficiente di sicurezza).

in base alla Wx che la tabella ci fornisce andiamo a scegliere il profilo della trave IPE, in questo caso abbiamo scelto una IPE300.

Per verificare che la trave sopporti il peso proprio, analogamente a prima aggiungiamo il peso nel carico strutturale

-trave IPE300 con peso specifico 0.422 KN/m che andremo a dividere per il nostro interasse 4m = 0.1055 KN/mq

qs = 1,7405+0,1055 = 1,846 KN/mq

La tabella ci restituisce una Wx=476.93 cm3 e l'IPE300 ha una Wx di 557 cm3, la trave è verificata.

TRAVE IN CALCESTRUZZO ARMATO

Solaio in latero-cemento con pignatte da 12x40x25 cm con interasse di 50 cm.

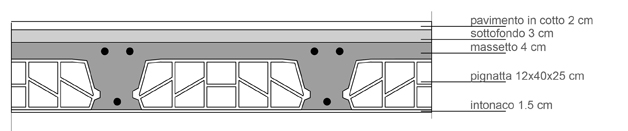
Il solaio sarà composto da:

1. strato d'intonaco con peso specifico di 11,5 KN/m3
2. pignatte peso specifico di 0.065 KN
3. travetti peso specifico 25 KN/m3
4. caldana di malta cementizia con p.s. 25 KN/m3
5. sottofondo composto da malta di calce con p.s. 18 KN/m3
6. pavimento in cotto con p.s. 18 KN/m3

CARICHI STRUTTURALI

-pignatte (12x40x25 cm) in un metro quadrato ci sono 8 pignatte, quindi il loro peso totale è di 0.52 KN

-travetti (s=10 cm) = (0,12m*0,10m*1m)*25 KN/m3 = 0,3 KN/mq dividiamo per l'interasse dei travetti = 0.6 KN/mq

-caldana (s=4 cm) = (0,04m*1m*1m)*25 KN/m3 = 1 kN/mq

qs = 0,52+0,6+1 = 2,12 KN/mq

CARICHI PERMANENTI

-intonacato (s=1,5 cm)  = (0,015m*1m*1m)*11,5 KN/m3 = 0,1725 KN/mq

-sottofondo (s=3 cm)= (0,03m*1m*1m)*18 KN/m3 = 0,54 kN/mq

-impianti = vengono calcolati circa 0,5 KN/mq

-tramezzi = vengono calcolati circa 1 KN/mq

-pavimento (s=2 cm) = (0,02m*1m*1m)*18 KN/m3 = 0,36 KN/mq

qp= 0,1725 + 0,54 + 0,5 + 1 + 0,36 = 2,5725 kN/mq

CARICHI ACCIDENTALI

- per civile abitazione 2 kN/mq

Inseriamo i dati nel foglio di calcolo, per l armatura si sceglie il B450C, classe di resistenza cemento RCK 450, impostiamo la base della trave a 20 cm.

Ci esce un altezza utile di circa 34 cm e una totale di 39, scegliamo una trave 20x45 cm.

Verifichiamo con l'inserimento del peso proprio della trave

-trave (20x45 cm) = (0.2m*0.45m)*25 KN/m3 = 2.25 kN/m dividiamo per interasse /4 =0.5625 KN/mq

qs = 2,12+0,5625= 2,6825 KN/mq

Ci viene un altezza di 40.22 cm, la trave è verificata.

ESERCITAZIONE SUL METODO DELLE FORZE_16-04-2013

Il metodo delle forze consente di risolvere strutture iperstatiche in maniera tutto sommato agevole, dal momento che la struttura oggetto d’analisi viene ricondotta ad una struttura isostatica di riferimento. Il concetto chiave di questo procedimento risiede nella nozione di compatibilità cinematica e di congruenza di spostamenti e/o rotazioni semplici, noti negli esempi di sistemi isostatici a cui ci si rifà.

Risolvendo uno degli esempi più comuni di struttura iperstatica, ovvero la trave continua su più appoggi, descriveremo per punti questo metodo di risoluzione.

• STRUTTURA IPERSTATICA DI PARTENZA

• STRUTTURA ISOSTATICA DI RIFERIMENTO

La struttura iperstatica di partenza viene ricondotta ad una isostatica nella quale, al numero di gradi di iperstaticità precedenti, corrispondono lo stesso numero di reazioni vincolari incognite in grado di non labilizzare la struttura in questione.

Nel nostro caso specifico abbiamo, quindi, 3 reazioni vincolari incognite (per il principio della simmetria x₁=x₃ d’ora in avanti si userà solo x₁) che si oppongono alla rotazione concessa dalle cerniere e precedentemente negata dai 3 vincoli.

• EQUAZIONI DI COMPATIBILITA’ CINEMATICA

Individuate le reazioni incognite, dobbiamo scrivere le equazioni di compatibilità cinematica capaci di ripristinare il vincolo iperstatico, soppresso attraverso la trasformazione dello stesso in reazione vincolare.

• RISOLUZIONE DELLE EQUAZIONI

Sostituendo alle equazioni di compatibilità cinematica i rispettivi valori delle rotazioni nei 3 nodi B,C e D e mettendole a sistema possiamo trovare i valori delle nostre due incognite x₁ ex_2.

Risolvendo questo sistema di 2 equazioni in 2 incognite troviamo i due valori delle nostre incognite x₁ e x₂.

• PRINCIPIO DI SOVRAPPOSIZIONE DEGLI EFFETTI

Definite le incognite delle reazioni vincolari x₁ e x₂ applichiamo in maniera sistematica il principio di sovrapposizione degli effetti, semplificando ulteriormente la struttura isostatica di riferimento mediante due strutture: una dipendente dal carico q e l’altra dipendente dalle reazioni vincolari x.

In entrambi i casi è possibile scomporre la struttura in 4 travi doppiamente appoggiate, studiare le reazioni vincolari dovute al carico q e ai momenti x₁ e x₂ in ognuna di queste 4 travi e sommare quelle relative ai medesimi nodi per avere le reazioni vincolari finali dei due sistemi.

q)

x)

A questo punto è possibile sovrapporre gli effetti dei due sistemi e avere lo schema delle reazioni vincolari della nostra struttura di partenza. Passaggio questo necessario al fine di poter diagrammare lo sforzo di Taglio e il Momento Flettente.

Reazioni vincolari

Taglio

Momento Flettente

Per  risolvere una struttura tre volte iperstatica (3 gradi di libertà e 6 gradi di vincolo, quindi con un numero di incognite maggiore al numero di equazioni di equilibrio), mi conviene visualizzare la trave come se non fosse un corpo unico su 5 appoggi, ma come se fosse una serie di travi doppiamente appoggiate.
In pratica per risolvere questo sistema iperstatico, uso un sistema isostatico di riferimento, a cui arrivo togliendo i tre gradi di vincolo che rendono iperstatica la struttura. In questo caso annullo la continuità della trave, dividendola in quattro corpi separati, eliminando quindi le tre reazioni vincolari interne che le terrebbero unite. In particolare trasformo le tre cerniere passanti degli appoggi B, C e D, in cerniere interne; permetto quindi una rotazione indipendente dei quattro corpi A-B, B-C, C-D, D-E. In corrispondenza delle cerniere applico poi il momento flettente che serve a ripristinare la continuità della trave. Con “X” indico la reazione vincolare interna.
La struttura assume così questo nuovo assetto:

Ho di conseguenza quattro sistemi isostatici.

Per risolvere il sistema parto dal trovare il valore dei tre momenti X₁,X₂ e X₃. Data la simmetria della struttura posso dire che X₁ = X₃. Cerco le incognite:

So che ΔϕB = ΔϕD=0 e ΔϕC=0

Ora uguagliando la rotazione a destra con quella a sinistra, dei punti analizzati, posso trovare i valori di X₁-X₃ e di X₂.

Il problema di avere tre gradi di vincolo di troppo è ora risolto! Conoscendo i loro valori posso procedere con facilità al calcolcolo delle reazioni vincolari. Applicando la sovrapposizione degli effetti, trovo le reazioni nei due sistemi di riferimento: iperstatico e isostatico.
Quindi una volta trovo le reazioni in base al carico distribuito q e poi le calcolo in base ai momenti X₁, X₂, X₃ come di seguito:

Sommo le reazioni vincolari trovate nei due sistemi:

Ora posso disegnare i diagrammi delle sollecitazioni di Taglio e Momento, trovando i valori nei vari punti.
Esempio di calcolo del diagramma del Momento:

Diagramma del taglio

Diagramma del momento